Theoretical study of the zero-gap organic conductor α-(BEDT-TTF)₂I₃

Abstract

The quasi-two-dimensional molecular conductor α-(BEDT-TTF)₂I₃ exhibits anomalous transport phenomena where the temperature dependence of resistivity is weak but the ratio of the Hall coefficient at 10 K to that at room temperature is of the order of 10⁴. These puzzling phenomena were solved by predicting massless Dirac fermions, whose motions are described using the tilted Weyl equation with anisotropic velocity. α-(BEDT-TTF)₂I₃ is a unique material among several materials with Dirac fermions, i.e. graphene, bismuth, and quantum wells such as HgTe, from the view-points of both the structure and electronic states described as follows. α-(BEDT-TTF)₂I₃ has the layered structure with highly two-dimensional massless Dirac fermions. The anisotropic velocity and incommensurate momenta of the contact points, ±k₀, originate from the inequivalency of the BEDT-TTF sites in the unit cell, where ±k₀ moves in the first Brillouin zone with increasing pressure. The massless Dirac fermions exist in the presence of the charge disproportionation and are robust against the increase in pressure. The electron densities on those inequivalent BEDT-TTF sites exhibit anomalous momentum distributions, reflecting the angular dependences of the wave functions around the contact points. Those unique electronic properties affect the spatial oscillations of the electron densities in the vicinity of an impurity. A marked behavior of the Hall coefficient, where the sign of the Hall coefficient reverses sharply but continuously at low temperatures around 5 K, is investigated by treating the interband effects of the magnetic field exactly. It is shown that such behavior is possible by assuming the existence of the extremely small amount of electron doping. The enhancement of the orbital diamagnetism is also expected. The results of the present research shed light on a new aspect of Dirac fermion physics, i.e. the emergence of unique electronic properties owing to the structure of the material.

• organic conductor
• α-(BEDT-TTF)2I3
• massless Dirac fermion
• zero-gap state
• tilted Weyl equation
• conductivity
• Hall conductivity
• orbital diamagnetism
• interband effects of magnetic field
• charge ordering
• charge disproportionation
• impurity effects

Introduction

In quasi-two-dimensional organic conductors, bis(ethylene dithiolo)tetrathiofulvalene (BEDT-TTF) salts [1], a large degree of freedom for arrangement and rotation of molecules gives rise to the emergence of various electronic states, such as superconductivity [2] and charge ordering [3]. Among many salts, the α-(BEDT-TTF)₂I₃ (α phase of BEDT-TTF tri-iodide) synthesized by Bender [4] is of particular interest, because it exhibits a rich phase diagram containing three unconventional electronic states, i.e. the stripe charge ordering, the superconductivity in the presence of charge ordering, and the zero-gap state (ZGS).

The metal–insulator transition was observed at T_MI=135 K at ambient pressure [4]. The magnetic susceptibility measurement at ambient pressure shows a rapid decrease at temperatures below T_MI indicating a nonmagnetic state with a spin gap [5]. The origin of the insulator phase has been studied theoretically using the mean field approximation [6–9], and the stripe charge ordering was proposed by introducing the extended Hubbard model with the on-site and nearest-neighbor Coulomb interaction [7]. From the nuclear magnetic resonance (NMR) experiments [10] and the angular dependence of ¹³C-NMR line shape, it was confirmed that the charge stripes run along the direction perpendicular to the a-axis [11]. The charge disproportionation that exists even above T_MI develops as temperature decreases from room temperature to T_MI [12]. The Raman studies suggest the charge ordering in the insulating phase below T_MI and also charge disproportionation above T_MI [13, 14]. Recent theoretical results on the charge disproportionation [15] are consistent with the x-ray experiment and NMR experiment [16, 17].

By adopting an experimental technique of uniaxial strain [18], it was observed that the superconductivity with the critical temperature T_c∼7 K emerges under the pressure (∼2 kbar) along the a-axis [19]. The mechanism of such superconductivity was investigated using the extended Hubbard model [20]. The paring mechanism that is mediated by the spin fluctuation has been maintained and interpreted in terms of the self-doped pseudo-one-dimensional Heisenberg chain.

In 1992, Kajita et al found anomalous transport phenomena in α-(BEDT-TTF)₂I₃, where the resistivity in the conducting BEDT-TTF plane exhibits weak temperature dependence but the Hall coefficient exhibits strong temperature dependence under high pressure, 14.7 kbar [21]. The Hall coefficient at low temperatures become 10⁵–10⁶ times larger than those at room temperature [19, 22–24]. Then it was called narrow-gap semiconductor, because it has the properties of both a metal and a semiconductor [19].

The band structure has been examined using the extended Hückel molecular orbital calculation based on the structure analysis by x-ray diffraction. The semi-metallic band structure with hole and electron pockets is obtained at ambient pressure [25, 26], although the insulator phase is observed at low temperatures. The volumes of the hole and electron pockets decrease under a-axis pressure while the volume of the hole pocket increases under b-axis pressure [27]. The electronic states of α-(BEDT-TTF)₂I₃ at higher pressures are investigated theoretically [20, 28, 29] to study the mechanism of the superconductivity. It is suggested that an unconventional state exists at pressures higher than a critical pressure where the charge ordering disappears. The density of states (DOS) in the unconventional state is proportional to |∊| with ∊ being the energy measured from the chemical potential. By extending this calculation, the energy dispersion of such electronic state is investigated theoretically using the transfer energies estimated from the experimental data under uniaxial pressure [27], then the Dirac cone dispersion is predicted [30, 31]. It is the ZGS where the chemical potential coincides with the contact points of two cones facing each other. The existence of the ZGS is verified by first-principles calculations [32, 33], which suggest the ZGS at ambient pressure. The tilted Weyl equation is proposed as the effective Hamiltonian describing the motion of electrons and holes in the vicinity of the contact point [34]. This equation reveals that the extremely anisotropic velocity of the massless Dirac fermion originates from the tilting of the axis of the isotropic cones.

The first discovery of Dirac fermion in condensed matter physics was in graphite [35]. The motions of electrons obey the Weyl equation that was used for neutrino, although the velocity is of the order of 10⁻³ of the light velocity [36–38]. Anomalous properties in transport phenomena, i.e. the Hall effect [39, 40], absence of the backward scattering [41], and universal conductivity [42, 43], have been elucidated on the bases of this equation in the context of a single layer in graphite structure, graphene [44]. The interband effects of vector potential have been elucidated for anomalous orbital diamagnetism and Hall effect in a weak magnetic field [45]. On the other hand, electrons in bismuth are described using the tilted Dirac equation [46] with small band gap and anisotropic velocities. The large diamagnetism of bismuth is due to the interband effects of magnetic field in these particular circumstances [47]. Electrons in the HgTe quantum well also obey the Dirac equation for either the zero-gap or the finite gap depending on the thickness of the quantum well [48].

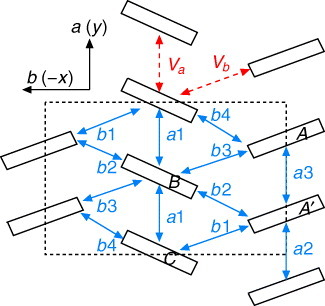
Compared with the conventional Dirac fermions, the ZGS of α-(BEDT-TTF)₂I₃ has several unique features. It has the layered structure with a highly two-dimensional electronic system. The interlayer transport phenomena, such as the interlayer magnetoresistance [49] and the interlayer Hall effects [50], exhibit many interesting behaviors. Particularly, it was theoretically shown that the strong negative interlayer magnetoresistance is due to the zero-mode Landau Level of the massless Dirac fermion [51]. NMR is also a powerful tool as introduced later. Low symmetry of the crystal due to the variety of transfer energies is also an important feature. The inequivalency of the BEDT-TTF sites (A(=A′)≠B≠C shown in figure 1) in the unit cell breaks point symmetries except the inversion symmetry. Tilting of the cones and the incommensurate contact point originate from the low symmetry. The tilting decreases the effective velocity of the cones [52].

Figure 1 Model for the electronic system of α-(BEDT-TTF)₂I₃ [3, 25]. The unit cell enclosed by a dotted line consists of four BEDT-TTF molecules with seven transfer energies t_a1, t_a2, t_a3, t_b1, t_b2, t_b3, t_b4 and two kinds of nearest-neighbor repulsive interaction, V_a and V_b corresponding to a and b directions. The a- and b-axes in the original notation [25, 26] correspond to the y- and x-axes in this paper.

Here, we note that the charge ordering is distinguished from the charge disproportionation as follows. The long-range ordering of charge induced by Coulomb interaction is called charge ordering. It accompanies the phase transition with symmetry-breaking. The difference in charge among the BEDT-TTF molecules in the unit cell, which comes from the inequivalency of those molecules, is called charge disproportionation. The inequivalency of molecules comes from the transfer energies or the local potential of anions. Then the charge disproportionation does not break any symmetry of crystal and does not have any phase transition. Recent theoretical results on the charge disproportionation [15] are consistent with the x-ray experiment [16] and NMR experiment [17]. The charge disproportionation exists in the ZGS theoretically [34]. The low symmetry induces the unconventional momentum distribution of the electron density in the vicinity of the contact point [34]. Moreover, many other variations of zero-gap organic conductors have been discovered [53]. Those unique features are expected to promote a new aspect of Dirac fermion physics.

The puzzle in the transport phenomena has been studied theoretically on the basis of the ZGS concept. The weak temperature dependence of resistivity is demonstrated using total band structure [54] and the relation between the quantum conductance in graphene [43] is discussed. Recently, a sharp but continuous change of the sign of the Hall coefficient has been observed at low temperatures [24]. To study the anomalous temperature dependences of the Hall coefficient, the Hall and electric conductivities are investigated theoretically for the massless Dirac electrons described using the tilted Weyl equation. The strong enhancement of the Hall coefficient toward low temperatures is shown [55] by taking the interband effects of magnetic field exactly into account in the Luttinger–Kohn representation and using the expected temperature dependence of the chemical potential [33]. The sharp but continuous reversal of the sign of the Hall coefficient is possible if the extremely small amount of electron doping, approximately 1 ppm, exists. These results can explain the very anomalous features of the Hall coefficient mentioned above. In addition, it is shown that the orbital diamagnetism has a peak at a temperature where the Hall coefficient reverses the sign. The strong temperature dependences of both the Hall coefficient and orbital diamagnetism are due to the interband effects of magnetic field.

In section 2, we describe the electronic states under pressure of α-(BEDT-TTF)₂I₃. The electronic properties of ZGS are shown in section 3. The anomalous transport phenomena and orbital diamagnetism are described in section 4. A summary is given in section 5.

Electronic states under pressure of α-(BEDT-TTF)₂I₃

Hamiltonian and mean field theory

The basic model describing the two-dimensional electronic system in α-(BEDT-TTF)₂I₃ is shown in figure 1 [3, 25]. The unit cell consists of four BEDT-TTF molecules with sites A, A′, B and C. There are six electrons in the four molecules, i.e. the 3/4-filled electronic system. The extended Hubbard model with the on-site repulsive interaction U and the anisotropic nearest-neighbor repulsive interaction V_αβ is given by [3, 28] where i and j denote site indices of the unit cell, and α and β (=A, A′, B and C) are indices of BEDT-TTF sites in the unit cell. The unit of energy is eV hereafter. In the first term, a^†_iασ denotes a creation operator with spin σ(=↑, ↓) and t_iα;jβ is the transfer energy between the (i, α) site and (j, β) site. The transfer energies under the uniaxial pressure (P_a) along the a-axis is estimated using the extrapolation formula The transfer energies t_X and coefficients K_X are given using the data at P_a=0 kbar [25] and at P_a=2 kbar [27], where t_a1(0)=−0.028, t_a2(0)=0.048, t_a3(0)=−0.020, t_b1(0)=0.123, t_b2(0)=0.140, t_b3(0)=−0.062, t_b4(0)=−0.025 (eV) and K_a1=0.089, K_a2=0.167, K_a3=−0.025, K_b1=0, K_b2=0.011, K_b3=0.032, K_b4=0 (eV kbar⁻¹). The charge ordering is calculated using the mean field theory [6–8, 28], where the Hamiltonian is given by where and (i.e. independent of the site i), , and δ denotes the vector representing the nearest neighbor of the unit cell. The Hamiltonian (3) is diagonalized by where ξ_rσ are the eigenvalue with the descending order, ξ_1σ(k)>ξ_2σ(k)>ξ_3σ(k)>ξ_4σ(k), and d_αrσ(k) (r=1, 2, 3, 4) are the corresponding eigenvectors. In terms of equation (6), the number of electrons on α-site with spin σ is given by where T is the temperature and the Boltzmann factor k_B is taken as 1. Equation (7) is the self-consistent equation for n_ασ. The chemical potential μ is determined by

Electronic states under pressure

We take V_a being larger than V_b to obtain horizontal stripe pattern [7, 11]. The phase diagram obtained from the mean field theory is shown in figure 2 on the plane of P_a and V_a with U=0.4, V_b=0.05, and T=0 [20]. The charge-ordered insulator exists for large V_a (V_a>0.167 at ambient pressure) and the charge-ordered metal appears continuously on the dashed line with decreasing V_a or increasing P_a. The charge orderings appearing in both those two phases are the horizontal stripe, and do not exhibit any phase transitions between them. Recent theoretical estimation on charge on each site [15], based on the transfer energies obtained by the first-principles calculation [33], is consistent with both the x-ray experiment [16] and the NMR experiment [12], where the A and B sites are hole-rich and the A′ and C sites are electron-rich. The ZGS emerges with a further increase of P_a. The phase transition from the metal to the ZGS is of the first order. The charge disproportionation due to the inequivalency of A(=A′), B and C sites exists in the ZGS. The charges of A and A′ sites are equivalent, because the inversion symmetry is not broken. The tendency that the B site is hole-rich and the C site is electron-rich is similar to that of the charge ordering. We emphasize that there are no long-range orders in this phase. The dotted blue line with V_a=0.17 is used to explain the P_a dependences of the electronic states observed in α-(BEDT-TTF)₂I₃ [23].

Figure 2 Phase diagram on the plane of P_a and V_a with U=0.4, V_b=0.05, and T=0 [20]. The dashed line denotes the boundary between the charge-ordered insulator and charge-ordered metal. The solid line denotes the boundary between the charge-ordered metal and ZGS.

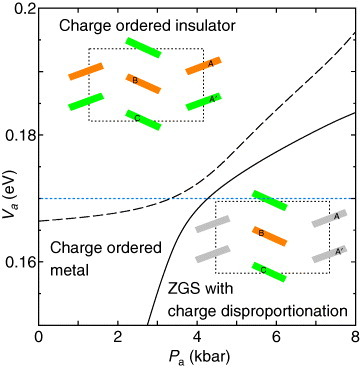
Figure 3(a) shows the P_a dependences of the band gap between the conduction and valence bands (filled circles) and the superconducting transition temperature T_c (open circles) with U=0.4, V_a=0.17, and V_b=0.05 [20]. The positive gap indicates the insulator, and the negative gap indicates the metal owing to the overlap of the conduction and valence bands. In the ZGS, the gap is always zero, indicating the robustness of the ZGS with varying pressure [31]. If the inversion symmetry is retained under some change in the transfer energies, the point degeneracy of those bands is topologically protected, while the contact points move in the first Brillouin zone. The superconductivity in the presence of the charge ordering, which is mediated by the spin fluctuation on the hole-rich chains, occurs in the charge-ordered metal [20], where the T_c is determined using the linearized gap equation for the superconductivity mediated by both the spin and charge fluctuations that are calculated by the random phase approximation on the basis of the site representation using the electronic states given by the mean-field theory. The T_c corresponds to the absolute value of the negative gap, and thus corresponds to the carrier density. We note that the staggered magnetic moments along the hole-rich sites (A and B) exist in the mean-field solution in both the charge-ordered insulator and charge-ordered metal phases, although the temperature dependence of the magnetic susceptibility indicates the spin-singlet formation at ambient pressure [5]. The singlet formation of the spins on the hole-rich sites in the insulator phase is expected if the strong correlation effect owing to the on-site Coulomb interaction U and the difference between the transfer energies t_b2 and t_b3 (see figure 1) are introduced. In the charge-ordered metal phase, however, the singlet is expected to be delocalized by the carriers in the sense of the resonance valence bond [56] resulting in the singlet superconductivity. Figure 3(b) shows the energy dependences of the DOS of the charge-ordered insulator at P_a=2 kbar (dashed line), the charge-ordered metal at P_a=4 kbar (solid line), and the ZGS at P_a=6 kbar (dot-dashed line) with U=0.4, V_a=0.17, and V_b=0.05. The superconductivity in the presence of the charge ordering occurs using the finite DOS near ω=0. The DOS in the ZGS exhibits the characteristic V-shaped energy dependence.

Figure 3 (a) P_a dependences of the band gap between the conduction and valence bands (filled purple circles) and superconducting transition temperature T_c (open circles with orange line) with U=0.4, V_a=0.17, and V_b=0.05 [20]. (b) Energy dependences of the DOS of the charge-ordered insulator at P_a=2 kbar (dashed red line), charge-ordered metal at P_a=4 kbar (solid black line), and ZGS at P_a=6 kbar (dot-dashed blue line) with U=0.4, V_a=0.17, and V_b=0.05 [20, 28].

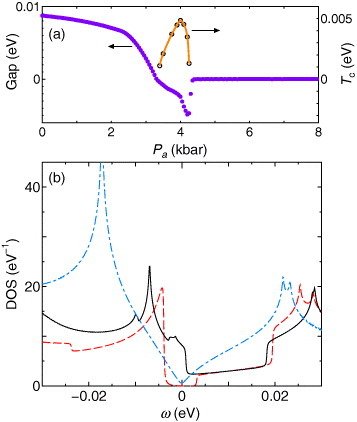
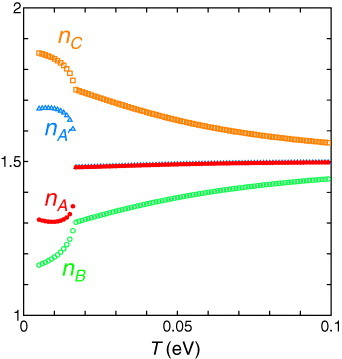
Figure 4 shows the T dependences of the electron numbers n_α (α=A, A′, B and C) at P_a=0, where U=0.4, V_a=0.17, and V_b=0.05 [34]. The charge-ordered insulator is obtained at T lower than T_CO=0.016. There exist staggered magnetic moments m_A(>0) and m_B(<0) on the hole-rich sites for T<T_CO, where . At the high-T region (T>T_CO), on the other hand, there is only the charge disproportionation with no magnetic moments m_α. There is no upper critical T for vanishing the charge disproportionation. We note that the contact points exist but the chemical potential slightly leaves the contact points. The first-principles calculation also indicates that the electronic system at ambient pressure has the contact points, although the chemical potential leaves the contact points with increasing T [33]. The charge disproportionation is essentially due to the inequivalency of the BEDT-TTF sites in a unit cell. However, both V_a and V_b are indispensable for reproducing the experimental results of the charge disproportionation.

Figure 4 T dependences of the electron numbers n_α (α=A (filled red circles), A′ (blue triangles), B (open green circles), and C (orange squares)) at P_a=0, where U=0.4, V_a=0.17, and V_b=0.05 (reproduced with permission from [34]).

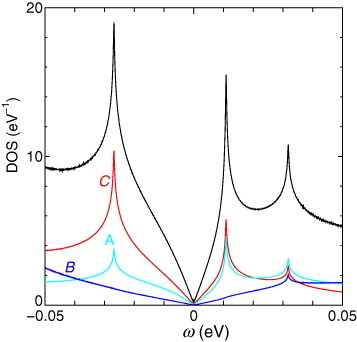
It is found that the DOS also reflects the inequivalence of the A (=A′), B and C sites. Figure 5 [15, 57] shows the DOS, ρ_α(ω), on each BEDT-TTF site α=A, A′, B, C in a unit cell, calculated using the data obtained by Kino and Miyazaki [33], where . These four components exhibit linear energy dependences in the vicinity of the contact point. However, the inclination of ρ_C(ω) is much higher than that of ρ_B(ω), and that of ρ_A(ω) (=ρ_A′(ω)) has an intermediate value. This indicates that the site C mainly contributes to the ZGS. The inclinations of ρ_α(ω) affect the properties induced by low-energy excitations, such as the Knight shift K and the 1/T₁ of the NMR experiments [15, 58, 59].

Figure 5 Density of states (DOS) in the vicinity of the contact point on the BEDT-TTF sites A, A′, B and C, where ω=0 corresponds to the chemical potential [15, 57].

Zero-gap state

Dirac cone and electronic structure in the ZGS

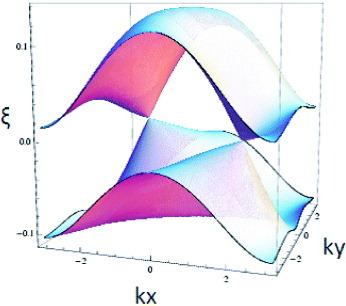
Figure 6 shows the energy dispersion of the conduction band ξ₁ and the valence band ξ₂ for U=0.4, V_a=0.17, and V_b=0.05, where the lattice constant is taken as a=1 [31]. The chemical potential coincides with the contact point at T=0. There are two contact points ±k₀ because of the inversion symmetry. The linear dispersion exists within approximately 100 meV around the contact point. The velocity in the vicinity of the contact points is extremely anisotropic. The highest velocity is approximately ten times larger than the lowest velocity corresponding to the opposite direction of the highest velocity. Such a Dirac cone dispersion was found using the transfer energies given by the extended Hückel method on the basis of the data of the x-ray experiment [27]. The global structure obtained using the transfer energies given by the first-principles calculation [33] is similar to that of figure 6.

Figure 6 Energy dispersion of the conduction band ξ₁ and valence band ξ₂ (<ξ₁), where the vertical axis represents the band energy in eV, on the k_x–k_y plane in radian [57]. The chemical potential is taken as zero.

The gap does not open in the presence of the charge disproportionation with varying pressure, except in the case that two contact points merge with each other at high pressure [34]. Figure 7 shows the trajectories of the contact points when the transfer energies as the function of P_a are calculated using the data of Kondo et al [27]. In the ZGS, the contact point moves from the cross (×) point (P_a=4.3 kbar) to the Γ point with increasing P_a along the solid line. At the phase transition from the ZGS to the charge-ordered state (at P_a=4.3 kbar), on the other hand, a pair of cones of the conduction and valence bands is split into two pairs of cones and gains the finite gaps simultaneously owing to the absence of the inversion symmetry and the spin-reversal symmetry [57]. The momentum where the gap of a pair of the bands opens is different from that of another pair. The gap of a pair with a relatively large width remains near the location of the contact point for the ZGS (the × point). The gap of another pair with a small width, however, jumps into another × point in the vicinity of the M′ point. We note that the small electron and hole pockets emerge in the charge-ordered metal, because the energy of the former pair increases and the energy of the latter pair decreases. In the charge-ordered insulator, the widths of the gaps exceed those deviations of band energies. The smallest gap is located at the M′ point at pressures lower than P_a=3 kbar.

Figure 7 The solid curves show trajectories of a pair of contact points ±k₀ that moves to the Γ-point with increasing P_a, where U=0.4, V_a=0.17, and V_b=0.05 [34]. The small ellipse of the solid line represents the electron and hole pockets for the charge-ordered metallic state at P_a=4 kbar. The dashed curves are obtained for the noninteracting case. The contact points also move from open-circle points (P_a=0 kbar) to the Γ point. The dashed curves around the X and Y points represent the electron and hole pockets, respectively, at P_a=0. The square, triangle and inverted triangle points correspond to P_a=10, 20, and 30 kbar, respectively (reproduced with permission from [34]).

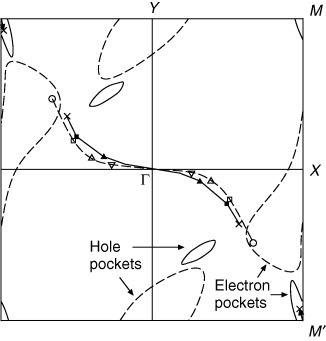
At high pressures, a pair of contact points approaches the Γ point, and then vanishes due to collision at P_a≅40 kbar. The electronic system becomes the Dirac fermion with finite mass at pressures higher than P_a≅40 kbar. The dashed curves in figure 7 are obtained for the noninteracting case, where the contact point also moves from the open-circle point (P_a=0 kbar) toward the Γ point.

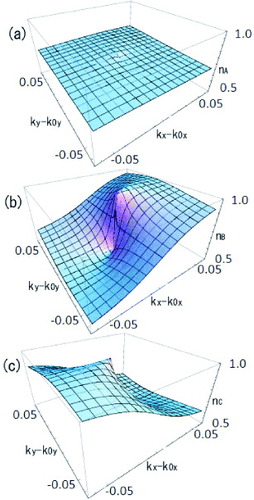
The momentum distributions of the charge density n_α(k) exhibit a singularity in the vicinity of the contact point, reflecting the inequivalence of the BEDT-TTF sites A (A′), B and C [34], where The singularity comes from the angle-dependent wave functions of the massless Dirac fermions on these inequivalent BEDT-TTF sites, d_αγσ(k), although the inversion symmetry exists for the equivalences of A and A′. Figure 8 shows the momentum dependences of n_A(k), n_B(k) and n_C(k) in the vicinity of the contact points [57]. The singularity with antisymmetry is found in n_B(k) and n_C(k). The behavior of the momentum dependence in n_B(k) is opposite to that of n_C(k). On the other hand, n_A(k) (=n_A′(k)) is almost independent of k, since the A and A′ sites are equivalent. The total charge density is, of course, independent of k. We emphasize that there are no singularities in n_A(k) and n_B(k) in graphene because the sublattices A and B are equivalent.

Figure 8 Momentum dependences of (a) n_A(k) (=n_A′(k)), (b) n_B(k) and (c) n_C(k) in the vicinity of the contact point k=k₀ [57].

The anomaly of the charge densities n_α(k) originates from the property of the wave function. In order to examine it, we start from a simple Hamiltonian which consists of 2 sites in a unit cell. In the case of graphite [41], a=b=0 and c=k_x−ik_y. The diagonal components become equal (a=b) and the off-diagonal components vanish (c=0) at the contact point of the two bands. The wave functions (the eigenvectors) of the Hamiltonian depend on the phase θ, where c=|c|e^iθ, i.e. θ is the angle of rotation around the contact point. The anomaly is discussed in terms of the helisity of the neutrino or the massless Dirac fermion in graphite. The wave function of the massless Dirac fermion can be described as that of the pseudo spin pointing a direction in the conducting plane. The helisity means that the pseudo spin is always parallel to the momentum k [43]. Becasue the components of the wave function are the functions of the angle θ, the components of the wave function jump from θ to θ+π when k passes the contact point into −k. Such discontinuity is an intrinsic property of the massless Dirac fermions.

The instability of the massless Dirac fermions in the presence of the site potential is also understood using H⁽²⁾. The diagonal components, which have different values in the presence of the site potential, violate the condition for degeneracy. Thus the massless Dirac fermions cannot exist in the system that consists of two inequivalent sites in the unit cell. For α-(BEDT-TTF)₂I₃, the massless Dirac fermions is robust against the charge disproportionation that originates from the inequivalency of the sites. It comes from the electronic system with four sites in a unit cell.

The unique properties of the ZGS in α-(BEDT-TTF)₂I₃ affect the electronic states in the vicinity of a nonmagnetic impurity [57, 60] corresponding to the lack of anions [61]. There appear the spatial incommensurate oscillation and anisotropy of the integrated DOS near the chemical potential in contrast to the case of graphene [62–68].

We discuss the stability of the zero-gap fermion against interactions or symmetry breaking. When the Hamiltonian has both inversion symmetry and time-reversal symmetry and without the spin–orbit interaction, the accidental degeneracy can occur on a line in the 3D momentum space [69]. The matrix representing the Hamiltonian can become real by unitary transform. Then two conditions, i.e. the diagonal elements are equal each other and the off-diagonal elements are zero, are required for degeneracy. The matrix becomes complex when either the inversion symmetry is broken or the spin–orbit interaction is finite. In this case, the degeneracy on the line disappears or remains on several points in the 3D momentum space [70, 71]. The α-(BEDT-TTF)₂I₃ has the inversion symmetry, although the extremely small spin–orbit interaction is expected to cause a possible finite energy gap, this will be ignored at finite temperature.

Spin magnetism

In this subsection, we examine the spin magnetism of the ZGS [15]. The spin susceptibility is described on the basis of four sites in a unit cell. The irreducible susceptibility is given by where iδ (δ>0) is an infinitesimally small imaginary part. The local magnetic susceptibility (Knight shift of NMR), χ_α, and the NMR relaxation rate, T₁, are obtained as [72, 73] respectively.

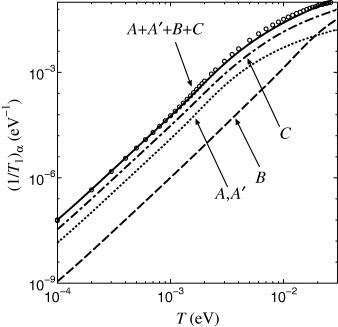
The local magnetic susceptibility and NMR relaxation rate for each site are shown in figures 9 and 10, respectively, as a function of temperature. The calculation is performed using the transfer energies at T=0 of the data obtained by Kino and Miyazaki [33]. The result obtained by taking the temperature dependences of the transfer energies into account is also shown for the total one (open circle) where such an effect of temperature is visible for T>0.005 eV. In figures 9 and 10, reflecting the DOS, χ_C and (1/T₁)_C are the largest among the four sites. At low temperature, χ_α and (1/T₁)_α are proportional to T and T³, respectively, owing to ρ_α(∊)∝|∊|. The local physical quantities, χ_α and (1/T₁)_α, reflect the electronic states in the vicinity of the Fermi energy. The difference in the DOS of the A(=A′), B and C sites in figure 5, which originates from the inequivalency of these sites, directly corresponds to the magnitude of χ_α and (1/T₁)_α. (If all the sites in the unit cell are equivalent, χ_α and (1/T₁)_α are independent of the sites.) We note that the electron numbers on the A(=A′), B and C sites, n_α, do not have direct correlation with the magnitude of χ_α or (1/T₁)_α, since n_α is given by the integration of the DOS from the bottom of the bands to the Fermi energy. The results of the χ_α shown in figure 9 are consistent with those of the NMR experiment [17], and n_α shown in figure 4 is consistent with the x-ray experiment [16]. The temperature dependence of the total 1/T₁ is similar to that of the NMR experiment [74, 75], although the temperature dependence exhibits a power being slightly different from 3. Such deviation may be attributable to the electron correlation effect.

Figure 9 Temperature dependences of χ_α (α=A,A′, B and C). The total value of χ_α is indicated by the solid line. The result of total one with the temperature dependence of the transfer energies is indicated by the open circles [15].

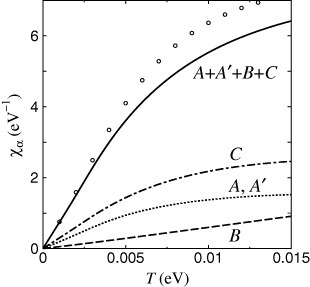
Figure 10 Temperature dependence of (1/T₁)_α. The notations are the same as in figure 9 [15].

Tilted Weyl equation

In this subsection, we use the bases of Luttinger–Kohn representation [76] to obtain the effective Hamiltonian in the ZGS [34]. In the Luttinger–Kohn representation, the k dependences of the basis of wave functions are the same as the plane waves, because the periodic functions u_kⁿ(r) in the Bloch's functions φ_kⁿ(r)=exp(ikr)u_kⁿ(r) with n being the band index are fixed on a constant momentum k=k_c. In the present case, we take k_c=k₀′, where k₀′ is infinitesimally close to the contact point k₀ to avoid the discontinuity of the phase of the Bloch's functions at k₀. Then we have the 4×4 matrix of the Hamiltonian, , where |γ〉 is the bases of Luttinger–Kohn representation with k_c=k₀′.

We can take the 2×2 part of the matrix corresponding to the conduction and valence bands and neglect other components when we describe the electronic states in the vicinity of the contact points. By making use of the expansion with respect to k, the Hamiltonian is given by The momentum k is measured from k₀′ hereafter. In the ZGS, H(0)=0 because the chemical potential coincides with the contact point. Then u_γγ′≡〈γ|∇H(k)|_k=0|γ′〉 is given by where τ=x, y denotes the spatial direction. The real vectors v_ρ are defined as respectively. Then we obtain the tilted Weyl equation [34] which is rigorous in the vicinity of the crossing point, where σ_{1, 2, 3} are the Pauli matrices, and σ₀ is the identity matrix. We take the Planck constant as . The energy dispersions ξ_k^±, corresponding to the conduction and valence bands, are obtained by diagonalization, where ν=1, 2, 3.

The angles and the length of the velocities v₁, v₂, and v₃ depend on the angle of the vector k₀′−k₀, although the resultant energy dispersion, of course, does not depend on the definition of k₀′. Those degree of freedom originates from the degeneracy of the bands at the contact point. The relations between the velocities and the eigenvectors are discussed in the next subsection. When k₀′−k₀ is parallel to the x direction, we can take v₀=(v₀, 0), v₁=0, v₂=(0, v_c) and v₃=(v_c, 0) approximately [15], where v_c=1.0×10⁵ m s⁻¹ and v₀=0.8×10⁵ m s⁻¹ based on the transfer energies given by the first-principles calculation [33].

Electronic structures close to the contact point

On the basis of the tilted Weyl equation, we examine the angle (θ) dependence of the eigenvectors of the mean-field Hamiltonian (equation (3)), d_αγ, where θ is the angle between k and the x-axis. We note that the eigenvector d_αγ(k) depends only on the angle, θ, in the vicinity of the contact point.

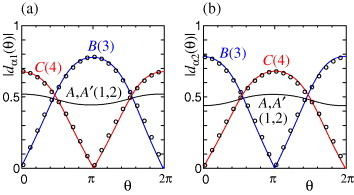
Figure 11 shows the θ dependence of |d_α1| (a) and |d_α2| (b) [15]. There is a node in the components of the B site and C site, e.g. d_B1(0)=0 and d_C1(π)=0. For θ∼0, |d_C1(θ)| is the largest, whereas |d_D1(θ)| is the largest for θ∼π. For A and A′, |d_α1(θ)| is almost constant. We note that there is a relation, |d_α1(θ)|=|d_α2(θ+π)|.

Figure 11 θ dependences of the absolute values of the eigenvectors of the mean-field Hamiltonian (equation (3)), |d_α1|(θ) in (a) and |d_α2|(θ) in (b). The open circles are obtained from equation (24) [15].

Here, we analyze the eigenvectors of the tilted Weyl equation. We discard the presence of v₀, because it gives only the uniform shift of the eigenvalue and then the components of the eigenvector are independent of v₀. By rewriting the tilted Weyl equation as we obtain for and , respectively, where k_x=k cos θ, k_y=k sin θ. The θ dependence of d_αγ is obtained as where u_αγ=d_αγ (k₀′). This gives |d_C1(θ)|=|d_B2(θ)|≃0.67|cos(θ/2)| and |d_B1(θ)|=|d_C2(θ)|≃0.78|sin(θ/2)|. These analyses reproduce well the results shown in figure 8.

We compare the present result with that of the graphene. For the latter case, the Hamiltonian of equation (22) is replaced by v(k_xσ₁+k_yσ₂), which gives the same eigenvalue but different eigenvector, where the absolute value of the component is independent of θ. The eigenvector of the graphene may correspond to the component of A and A′ of the present case, in which the θ dependence is small. Thus, it is found that the existence of the B and C components of the present case is the characteristic of the massless Dirac fermion of organic conductor α-(BEDT-TTF)₂I₃ in which there are four sites in the unit cell.

Anomalous transport phenomena and orbital diamagnetism

Conductivity, Hall conductivity, and orbital susceptibility in the tilted Weyl equation

In this subsection, we focus on the conductivity, the Hall conductivity, and the orbital susceptibility [55] in the tilted Weyl equation [34] obtained in the Luttinger–Kohn representation [76]. The interband effects of the magnetic field are taken into account exactly in the Luttinger–Kohn representation [47, 77]. The interband effects of magnetic field play crucial roles in the transport phenomena and the properties owing to orbital motion, such as the orbital diamagnetism [45, 78–80]. The electronic states in periodic potential of the crystal are described using the Bloch bands ∊_kⁿ. One may think that the description of the electronic states in the presence of the magnetic field is realized by the substitution k→k+e/cA in ∊_kⁿ, where A is the vector potential. However, this is not justified, because A has matrix elements between different Bloch bands. Mathematically, this is because the Bloch's functions are not plane waves but contain periodic functions u_kⁿ(r). On the other hand, in the Luttinger–Kohn representation [76], k dependences of the basis of wave functions are the same as plane waves, and then the substitution of k→k+e/cA is justified in the Luttinger–Kohn representation.

The conductivity and Hall conductivity are given by the Kubo formula, where μ and ν denote x or y, and ω_λ=2λπT is the Matsubara frequency. The current J is given by , where is the Hamiltonian with external magnetic field, . The vector potential is expressed as a plane wave A(r)=exp(iqr)A_q.

The conductivity is given by where G denotes the Green's function defined as with the Matsubara frequency ∊_n=(2n+1)πT, and G(+) denotes the Green's function with ∊_n→∊_n+ω_λ. The effective spectrum broadening due to elastic impurity scatterings at T=0, Γ₀, is taken into account phenomenologically here by .

The Hall conductivity σ_xy with weak magnetic field is given by the first-order terms of the vector potential and momentum q. The gauge-invariant formula of the Hall conductivity in the Luttinger–Kohn representation is given by

The orbital susceptibility is defined as

The orbital susceptibility in the weak magnetic field is given as the Fukuyama formula [78], In the Luttinger–Kohn representation, we obtain γ_x=v₀σ₀+v_cσ₁ and γ_y=v_cσ₃ for the tilted Weyl equation.

The chemical potential (μ) dependences of σ_xx, σ_xy, and χ were calculated for graphene [45]. The strong μ dependences of σ_xy and χ were found when μ is close to zero (the contact point). The tilting effects for σ_xx, σ_xy, and χ were calculated in the tilted Weyl equation [55].

Figure 12 shows the conductivities σ_xx, σ_xx^a, and σ_xx^b when the degrees of tilting α=v₀/v_c equal zero, where X=μ/Γ₀ represents the chemical potential scaled by Γ₀, and σ_xx=σ_xx^a+σ_xx^b. While σ_xx^a is independent of X, σ_xx^b exhibits weak X dependence in the vicinity of X=0 and is linear for |X|≫1. The finite value of the conductivity, e²/π², at X=0 is a remarkable feature of the zero-gap fermion. The total conductivity σ_xx is weakly enhanced by tilting as shown in the inset, which is due to the enhancement of σ_xx^b.

Figure 12 X dependences of total conductivity σ_xx (black line), σ_xx^a (red line), and σ_xx^b (blue line) when the degree of tilting α=0, where σ_xx⁰≡e²/2π² [55]. The inset shows X dependences of total σ_xx for several degrees of tilting.

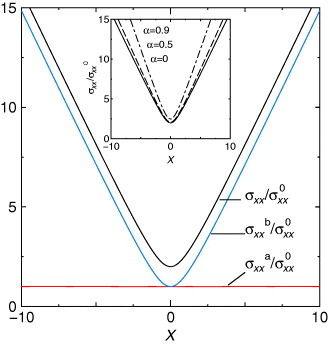
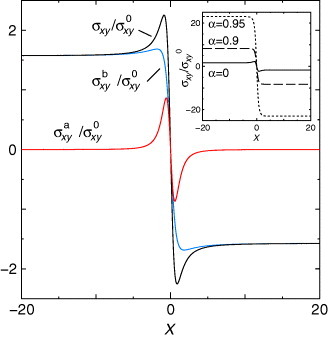
Figure 13 shows the Hall conductivities σ_xy, σ_xy^a, and σ_xy^b in the absence of tilting α=0, where σ_xy=σ_xy^a+σ_xy^b. The contribution of the interband effects of the magnetic field, σ_xy^a, exhibits strong X dependences in the vicinity of X=0 within the energy scale of Γ₀, and pass zero at X=0. The total Hall conductivities σ_xy for several degrees of tilting are shown in the inset. The Hall conductivity diverges when α=1. This divergence results from the integration over the Fermi surface extending to infinity. In the actual crystal, the divergence is suppressed by momentum integration in the finite Brillouin zone.

Figure 13 Hall conductivities σ_xy (black line), σ_xy^a (red line), and σ_xy^b (blue line) in the absence of tilting, where σ_xy⁰≡e³v_c²H/4π²cΓ₀² [55]. The inset shows X dependences of total σ_xy for several degrees of tilting.

The enhancements of σ_xx and σ_xy by tilting are related to the decrease in the renormalized velocity in the presence of tilting [52]. In addition, the roles of the interband effects of magnetic field in σ_xy were clarified by comparing with the intraband (Bloch) approximation [80–84].

Hall effect and orbital diamagnetism

To investigate the temperature dependence of the Hall coefficient in α-(BEDT-TTF)₂I₃, the temperature dependence of the chemical potential μ is taken into account. The temperature dependence of μ based on the tight-binding model with transfer integrals fitted to the first-principles calculation [33] is indicated by the dashed line in figure 14 [55]. In addition, the possible temperature dependence of the effective spectrum broadening due to the inelastic scattering is also taken into account phenomenologically, i.e. Γ₀ is replaced by Γ=Γ₀+θT, where θ is the coefficient of the linear term of T [55]. Γ₀=10⁻⁵ eV and θ=2×10⁻³ (dimensionless) are chosen hereafter. The three-dimensionality effects are taken into account by adding a term −2t_z cos k_za_z in addition to the tiled Weyl equation, where t_z is the interlayer hopping and a_z is the layer spacing 1.74×10⁻⁹ m [55]. The interlayer hopping t_z creates the spindle-shaped Fermi pockets with electrons and holes along the crossing line as schematically shown in the inset of figure 14.

Figure 14 Temperature dependences of the chemical potential μ in the presence of electron doping (1.6 ppm) with Δμ=2.0×10⁻⁴ (solid red line), and in the absence of the carrier doping (dashed blue line) [57]. The inset shows the spindle-shaped Fermi pockets with electron and hole along the crossing line due to the weak interlayer hopping.

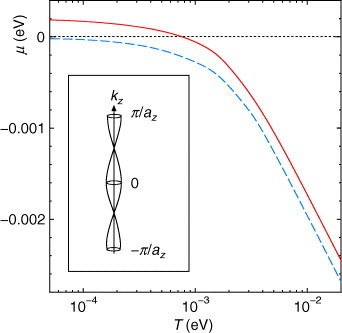
To explain the sign reversal of the Hall coefficient, we assumed the existence of electron doping, which is possibly induced by the lack of I₃⁻ ions [55]. The solid line in figure 14 shows the temperature dependences of μ in the presence of electron doping (1.6 ppm) with Δμ=2.0×10⁻⁴, where μ=Δμ at T=0. When electrons are doped, μ crosses zero at the finite temperature T_r. The value of Δμ=2.0×10⁻⁴ is chosen hereafter.

Figure 15 shows the temperature dependences of the conductivity with t_z=10⁻⁵, 3×10⁻⁵, 10⁻⁴, 3×10⁻⁴, and 10⁻³, where σ_xx⁰≡e²/2π² [85]. In the case with t_z=10⁻³, the conductivity exhibits weak temperature dependence but the value at T→0 is much higher than σ_xx⁰. The temperature dependences of the conductivity become strong with decreasing t_z. The conductivity decreases with decreasing T in the high-temperature region, and has a minimum at T_r and then weakly increases at temperatures lower than T_r. The minimum value of the conductivity is close to e²/π² at t_z=10⁻⁵, while the value has been studied as the quantum transport in graphene [43, 45, 86]. In α-(BEDT-TTF)₂I₃, the conductivity close to e²/π² has been observed at T=10 K (10⁻³ eV) [49], indicating t_z≅10⁻⁵. At temperatures lower than 10 K, however, it has been observed that the conductivity decreases with decreasing T. This decrease in conductivity may be due to the localization effect or the residual charge ordering.

Figure 15 Temperature dependences of the conductivity with t_z=10⁻⁵ (the black line), 3×10⁻⁵ (the red line), 10^{- 4} (the orange line), 3×10⁻⁴ (the green line), and 10⁻³ (the blue line) where σ_xx⁰≡e²/2π² [57].

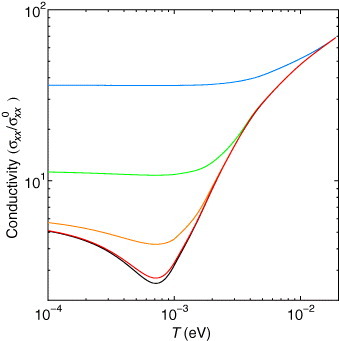
Figure 16 shows the temperature dependences of the Hall conductivity with t_z=10⁻⁵, 3×10⁻⁵, 10⁻⁴, 3×10⁻⁴, and 10⁻³, where σ_xy⁰≡e³v_c²H/4π²cΓ₀². In the case of t_z=10⁻³, the Hall conductivity exhibits weak temperature dependence and the values at low temperatures are close to zero. The temperature dependences of the Hall conductivity become strong and exhibit a sharp sign reversal at T_r for small t_z.

Figure 16 Temperature dependences of the Hall conductivity with t_z=10⁻⁵ (black line), 3×10⁻⁵ (red line), 10⁻⁴ (orange line), 3×10⁻⁴ (green line), and 10⁻³ (blue line), where σ_xy⁰≡e³v_c²H/4π²cΓ₀² [57].

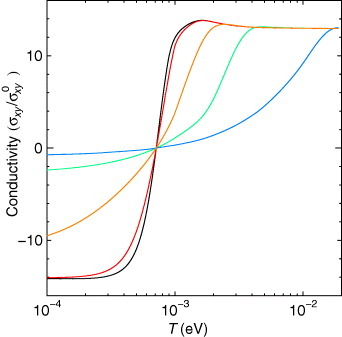
Figure 17 shows the temperature dependences of the Hall coefficient R with t_z=10⁻⁵, 3×10⁻⁵, 10⁻⁴, 3×10⁻⁴, and 10⁻³, where R=σ_xy/Hσ_xx² with R₀=π²v_c²/ecΓ₀². The Hall coefficient is strongly enhanced with decreasing T from room temperature to T_r. The sign of the Hall coefficient reverses continuously at T_r, because μ crosses zero. The sharpness of the reversal increases with decreasing t_z. The maximum Hall coefficient at T_m also increases with decreasing t_z, and then the maximum is 10³ times larger than that at room temperature when t_z is smaller than 10⁻⁴, which is in qualitative agreement with experimental observation in α-(BEDT-TTF)₂I₃ [24]. The inset shows t_z dependence of the half-width of the reversal, T_W≡T_m−T_r. When t_z is larger than Γ∼10⁻⁵, T_W decreases with decreasing t_z. When t_z is smaller than Γ, on the other hand, the temperature dependences of the Hall coefficient are ruled by Γ, and then T_W becomes independent of t_z. Then t_z must be comparable or smaller than Γ to explain the very sharp sign reversal observed in α-(BEDT-TTF)₂I₃ [24].

Figure 17 Temperature dependences of the Hall coefficient with t_z=10⁻⁵ (black line), 3×10⁻⁵ (red line), 10⁻⁴ (orange line), 3×10⁻⁴ (green line), and 10⁻³ (blue line), where R=σ_xy/Hσ_xx² with R₀=π²v_c²/ecΓ₀² [57]. The inset shows t_z dependence of the half-width of the reversal, T_W=T_m- T_r.

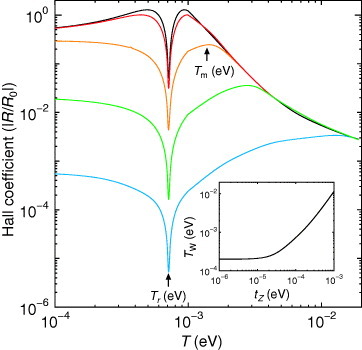
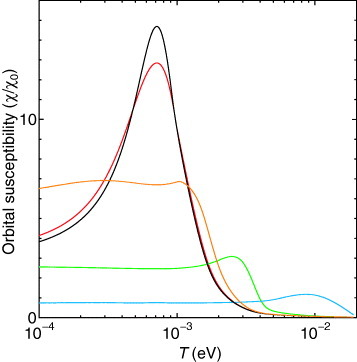
Figure 18 shows the temperature dependences of the orbital susceptibility with t_z=10⁻⁵, 3×10⁻⁵, 10⁻⁴, 3×10⁻⁴, and 10⁻³, where χ₀≡−e²v_c²/3π²c²Γ₀. The temperature dependence becomes strong with decreasing t_z. When t_z is smaller than 10⁻⁴, a characteristic peak emerges at T_r and grows with decreasing t_z.

Figure 18 Temperature dependences of the orbital susceptibility with t_z=10⁻⁵ (black line), 3×10⁻⁵ (red line), 10⁻⁴ (orange line), 3×10⁻⁴ (green line), and 10⁻³ (blue line), where χ₀≡−e²v_c²/3π²c²Γ₀ [57].

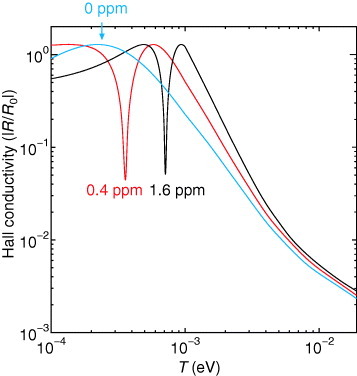
The electron-doping dependence of the Hall coefficient is shown in figure 19. The sign reversal of the Hall coefficient does not occur in the absence of the electron doping (dot-dashed line). The reversing temperature T_r increases as the electron doping increases. Surprisingly, it is theoretically predicted that the extremely small amount of electron doping, 1.6 ppm, gives T_r∼7 K, which is close to the experimental observations [24].

Figure 19 Electron doping dependence of the Hall coefficient as a function of T, where the black, red, and blue lines are calculated with Δμ=2.0×10^{- 4} (1.6 ppm), Δμ=1.0×10^{- 4} (0.4 ppm), and Δμ=0 (0 ppm), respectively [55].

We emphasize that the sensitivities of the Hall coefficient and orbital diamagnetism as functions of temperature are essentially due to the interband effects of the magnetic field. However, the present results indicate that high two-dimensionality is required for the appearance of characteristic phenomena due to the two-dimensional zero-gap fermions. The interlayer hopping could be controlled using the uniaxial pressure perpendicular to the conducting plane, and then experiments on transport phenomena and orbital diamagnetism are expected by varying the uniaxial pressure along the c-axis in α-(BEDT-TTF)₂I₃ to observe the dimension crossover.

Summary

The existence of the ZGS with the massless Dirac fermions was found in α-(BEDT-TTF)₂I₃ [30, 31], and the electronic properties have been investigated theoretically [20, 28, 29, 34]. α-(BEDT-TTF)₂I₃ is a unique material among several materials with Dirac fermions, i.e. graphene, bismuth, and quantum wells such as HgTe. Those massless Dirac fermions are described by the tilted Weyl equation which consists of the identity matrix and the Pauli matrices. Within the extrapolation scheme of the transfer energies, the pair of the contact points ±k₀ merges to disappear at high pressures, resulting in the Dirac fermions with finite mass as shown in the case of bismuth. The present massless Dirac fermions is robust against the pressure and charge disproportionation. The charge disproportionation originates from the inequivalency of BEDT-TTF sites, while the observed values of charge are reproduced by taking the interactions into account. The anomalous momentum dependence of the charge density in the vicinity of ±k₀ is also obtained. The anomaly comes from both the property of the wave function of the massless Dirac fermions and the inequivalency of BEDT-TTF sites.

In addition, the conductivity, Hall conductivity and orbital susceptibility in the tilted Weyl equation were calculated [55]. It is shown that these quantities have the same chemical potential dependences as those in the absence of tilting, where the Hall conductivity and orbital susceptibility are extremely sensitive to μ owing to the interband effects of magnetic field. These quantities are enhanced by tilting. Based on these results, the temperature dependence of the Hall coefficient is investigated by considering the temperature dependence of μ, which is estimated from the first-principles calculation of α-(BEDT-TTF)₂I₃ [33] together with that of the spectrum broadening and the three-dimensionality. It is shown that temperature dependence of the Hall coefficient accounts for the general features observed in α-(BEDT-TTF)₂I₃ [23]. To explain the sign reversal of the Hall coefficient [24], the existence of electron doping is assumed which is possibly induced by the lack of I₃⁻ ions. A sharp but continuous sign reversal of the Hall coefficient at low temperature is found, which is in qualitative agreement with the experimental observations. These results indicate firmly the existence of the zero-gap fermion. It is predicted theoretically that the extremely small amount of electron doping, 1.6 ppm, gives a reasonable reversing temperature of the Hall coefficient, T_r∼7 K, which is close to the experimental observations. Moreover, the peak of the orbital diamagnetism around T_r as a function of temperature is predicted, where the maximum value of the orbital diamagnetism can be of O(10⁻²) of the perfect Meissner diamagnetism.

The roles of the interlayer hopping are also investigated in the conductivity, Hall conductivity, and orbital susceptibility. It is found that the continuous reversal of the sign of the Hall coefficient increases the sharpness with decreasing interlayer hopping. The interlayer hopping should be comparable or smaller than the effective spectrum broadening, expected as 10⁻⁵ eV, to explain very the sharp sign-reversal observed in α-(BEDT-TTF)₂I₃. On the other hand, the spin density wave is investigated theoretically for the case with large interlayer hopping [87].

Lastly, the unique features of α-(BEDT-TTF)₂I₃ are expected to promote the original development that will shed light on new aspects of Dirac fermion physics. Particularly, the layered structure with highly two-dimensional massless Dirac fermions may exhibit new phenomena. Together with the effects of magnetic field, the layered structure is expected to affect the interlayer transport such as the interlayer Hall effect, electron correlation effects, and possible marginal Fermi liquid behavior with the resonance of polarization function.

Acknowledgments

We are indebted to R Kondo and S Kagoshima for providing the data of transfer energies in α-(BEDT-TTF)₂I₃ prior to their publication. We acknowledge H Fukuyama for encouraging us at the early stage of the work and also for the collaborative study on the tilted Weyl equation, Hall effect and orbital diamagnetism. We are also thankful to Y Fuseya, C Hotta, K Kajita, K Kanoda, H Kino, S Komaba, K Miyagawa, T Mori, S Murakami, T Nakamura, Y Nishio, K Noguchi, T Osada, H Seo, Y Shimizu, S Sugawara, N Tajima, T Takahashi, Y Takano, T Tohyama, K Yakushi, H Yamamoto, H Yoshioka, and G Montambaux for fruitful discussions. This work has been financially supported by a Grant-in-Aid for Special Coordination Funds for Promoting Science and Technology (SCF) from the Ministry of Education, Culture, Sports, Science and Technology of Japan, and for Scientific Research on Priority Areas of Molecular Conductors (No. 15073213) from the Ministry of Education, Culture, Sports, Science and Technology of Japan.