A novel relationship between the radical-scavenging activity of flavonoids and enthalpy of formation revealed with Hartree–Fock computations and thermochemical deduction

Abstract

Objective

The present study aims to establish the relationship between the reported radical-scavenging activities of flavonoids and some enthalpy changes that may occur during flavonoids' reactions with free radicals.

Method

Eight flavonoids were chosen for the study on the basis of their structural merits and reported 1,1-diphenyl-2-picryl-hydrazyl scavenging activities. Enthalpy changes accompanying interconversions between selected conformations (including spin multiplicities) and homolytic dissociations were estimated.

Results

A novel relationship exists between the total enthalpy of reaction for the abstraction of two hydrogen atoms from flavonoids, their reported radical-scavenging activities and the enthalpy of the homolytic dissociation of hydrogen molecule (104.206 kcal mol⁻¹). Only those flavonoids which could give up two hydrogen atoms with total enthalpy changes well below 104.206 kcal mol⁻¹ were active radical scavengers.

Discussion

By appealing to equilibrium dynamics, we demonstrated that, for flavonoids to be able to donate hydrogen atoms, the change in enthalpy accompanying the abstraction of two hydrogen atoms needs to be less than 104.206 kcal mol⁻¹. This condition does not seem to be restricted to flavonoids only but rather generally applicable to chian-breaking antioxidants.

Conclusion

Thermodynamical relationships may be the most important factors governing the radical-scavenging reactions of flavonoids and possibly other compounds as well. Nevertheless, a more complete characterization of antioxidants would necessitate kinetic analysis.

Keywords:

• Flavonoids
• Free radical scavengers
• Antioxidants
• Oxidation–reduction
• Hydrogen bonding
• Molecular conformation
• Thermodynamics

View correction statement:

A novel relationship between the radical-scavenging activity of flavonoids and enthalpy of formation revealed with Hartree–Fock computations and thermochemical deduction

Introduction

A suitable parameter for describing the abstraction of a hydrogen atom from the O–H bond of flavonoids is the difference in heat of formation of the parent and corresponding radical structures (ΔH_f), the value of which is principally dictated by the delocalization possibilities in the later.¹ On the basis of this premise, a few attempts have been made to elucidate the structure–radical-scavenging activity relationships of flavonoids^2,3 and related simple phenolic compounds.⁴ In our previous report,³ we introduced largely arbitrary cut-off points for ΔH_f, which were used as primary predictors of activity. The idea of cut-off points emanated from the observation that there was a sudden change in the half-maximal inhibitory concentration (IC₅₀) vs. ΔH_f curve around a certain point. However, the physical meaning of such cut-off points was not understood at the time. Nevertheless, this kind of discontinuity in a continuum quantity like ΔH_f was rather curious.

In line with this, Amić et al.⁵ have confirmed the presence of an activity cliff in the radical-scavenging activity of flavonoids, on the basis of a QSAR model derived from a descriptor for bond dissociation enthalpy (BDE). This indicated that there might be some common elements influencing the thermodynamic and kinetic aspects of the chain-breaking abilities of flavonoids. Recently, we have attempted to investigate the thermodynamics and kinetics of hydrogen atom abstraction from flavonoids and related phenolic compounds, using theoretical computation, with the aim to shed light on the aforementioned hypothesis of ours. In this communication, we have presented our findings on the relationship between change in heat of formation (ΔH_f) (here in referred to as, enthalpy change or ΔH°(298 K)) and reported 1,1-diphenyl-2-picryl-hydrazyl (DPPH)-scavenging activities of selected flavonoids.

Method

Computational details

The dihydroxyflavonoids studied were 3′4′-dihydroxyflavone, 7,8-dihydroxyflavone, 3,7-dihydroxyflavone, 3,4′-dihydroxyflavone, 3,3′-dihydroxyflavone, 5,7-dihydroxyflavone, 4′,7-dihydroxyflavone, and 3′,5-dihydroxyflavone. The flavonoids were selected on the basis of their structural merits and reported DPPH scavenging activities.^3,6–8

A typical procedure for generating input coordinates for computational analysis involved the following steps; the three-dimensional (3D) model of a flavonoidal structure was generated in ChemBio3D^® Ultra by directly typing its name. Alternatively, the structure could be drawn in ChemBioDraw^® Ultra 12.0.2 and pasted on to ChemBio3D^®. The 3D model was then pre-optimized with MMFF94 (molecular mechanics force-field calculation) implemented in ChemBio3D^® Ultra. The resultant geometry was at least once again optimized with RM1 (Recife Model 1) or AM1 (Austin Model 1) employing MOPAC 2009™ for ChemBio3D 12.0 and the result was saved in gif (Gaussian input file) format. Input geometries were sometimes generated using the graphical interface Gabedit,⁹ which otherwise was mainly used for visualization (all Gabedit figures were generated at an isovalue of 0.005).

The pre-optimized structures were then minimized with the ab initio Hartree–Fock hamiltonian (restricted or unrestricted) implemented in the quantum chemical program Gaussian 03^® E.01.¹⁰ Maximum effort was exerted to locate global minimum energies by exhaustively considering all the possible hydrogen-like interactions. Routinely, the initial guess was carried out in the default procedure for Gaussian 98 (Guess = INDO) (www.gaussian.com) and self-consistent field (SCF) convergence was sought following the conventional SCF with the old 3- and 4-point extrapolation (SCF = NoDIIS) or quadratically convergent SCF (SCF = QC, with or without full linear search). All optimized wave functions were tested for stability before used for harmonic frequency analysis. Unless a transition state was investigated, the maximum tolerated negative frequency (imaginary frequency) was −2.5 cm⁻¹. In addition, the SCF spin-densities of the optimized structures were computed. For almost all neutral molecules, both their important singlet and triplet states and for radical derivatives, important doublet and quartet states were considered. All Gaussian computations were carried out at 6–31G(d,p) basis set and Gaussian thermochemical quantities are for 298.150 K and 1.00000 Atm. Extreme care has been exercised in selecting the spin-density distributions that were most appropriate for the conformations of interest. All Gaussian computations were performed on either the high-performance computation facilities of Intersect Australia Limited (mclaren.ac3.edu.au/ shared memory SGI Altix 4700, 128 Dual-Core CPUs, 1TB RAM and 12 TB disk space) or the National Computational Infrastructure (NCI) National Facility (vayu.nci.org.au/ Sun Constellation Cluster, 1492 nodes, each containing 2 quad core Nehalem processors summing up to 11 936 cores, 37TB RAM and 800 TB disk space).

In the early stages of this study, attempts were also made to employ density functional theory (DFT) (particularly Becke three-parameter exchange and Lee-Yang-Parr correlation functional (B3LYP)),¹¹ double hybrid forms of density functional with an empirical dispersion term (particularly a semiempirical hybrid density functional with perturbative second-order correlation; B (Becke), 2 (number or parameters and the order of perturbation theory), PLYP (perturbative correlation with Lee-Yang-Parr functional), D (empirical dispersion term) (B2PLYP-D))^12,13 and second-order Møller–Plesset perturbation theory (MP2),^14,15 in addition to ab initio Hartree–Fock. Whereas B3LYP and MP2(Full) were in general carried out with Gaussian 03^® E.01¹⁰ in a more or less similar fashion as described for HF, Gaussian 09^® B.01¹⁶ on vayu.nci.org.au was used for B2PLYP-D works. For all these three post Hartree–Fock methods both their restricted and unrestricted programs were used where found appropriate. Ultrafine grid was used for numerical integrations in all B3LYP computations (Integral(UltraFineGrid)). Minimizations with MP2(Full) were generally started from HF optimized geometries and their force constants in Cartesian coordinates (from frequency calculations) (Opt = RCFC). Multiplicity, stability tests, harmonic frequency analyses, and Mulliken population analyses were similar to that described for HF. All post-HF Gaussian computations (see Supplementary Information) refer to 6–31G(d,p) basis set, 298.150 K and 1.00000 Atm. Mulliken population analyses were carried out with the default procedures for each method.

Determination of enthalpy changes

Scores of enthalpy changes (Eq. (1)) associated with conformational changes (including those involving spin states) and bond homolysis were estimated. Estimations of enthalpy changes were made by taking the appropriate sums and difference of the unscaled, i.e. default ‘sum of electronic and thermal energy’ terms from the harmonic frequency job outputs (Eq. (2)).¹⁷ The conversion factor used was 627.50944796 kcal mol⁻¹ H⁻¹. 1 2 where Δ_fH°(298 K) is the enthalpy of formation; x is the transformation, e.g. reaction (r) and conformational change (C); ɛ₀: total electronic energy (SCF); and H_corr is the ‘thermal correction to enthalpy’ from Gaussian frequency job output.

In accordance with our reaction model (described in a later section), for all the eigth dihydroxyflavonoids included in this study, enthalpy changes accompanying the homolytic bond dissociations of both hydroxyl groups and various conformational changes were estimated. Maximum effort has been made to minimize overlapping of processes and consequent errors in calculating the respective enthalpy changes. For instance, when approximating the enthalpies for the homolytic bond dissociations of hydroxyl groups, enthalpies resulting from any other significant interactions such as hydrogen bonding were carefully eliminated. Once again, utmost care was also taken in selecting the most appropriate corresponding pair of structures or conformations, in order to calculate a given enthalpy change. In relation to this, the spin-density distributions of such pairs were strictly matched, whenever possible (this of course does not concern equivalent spin-density distribution patterns, which only differ in terms of sign of spin).

Results

Stability tests revealed that restricted Hartree–Fock (RHF) always yielded unstable solutions for singlet states of the flavonoids studied. The instability was consistently of the type ‘RHF -> unrestricted Hartree-Fock (UHF)’, which strongly suggested that flavonoids were better treated as diradicals. Diradicals are molecular species having two unpaired electrons, in which at least two different electronic states with different multiplicities viz. electron-paired (singlet state) or electron-unpaired (triplet state) can be identified.¹⁸ This observation lent support to the necessity of spin-density distributions for a better description of flavonoids. Therefore, all further computations were undertaken using UHF.

As would be expected, MP2 also behaved similarly in stability tests since it is based on HF-linear combination of atomic orbitals (LCAO).¹⁹ Since all RMP2 solutions exhibited instability of the type ‘RHF -> UHF’, only unrestricted second-order Møller-Plesset perturbation theory (UMP2) was implemented. However, convergence for UMP2 treatment of our flavonoids proved to be difficult and erratic (results not shown).¹⁹ Even when convergence was achieved, excessive distortions of molecular geometries were frequent. Such distortions usually involved torsion angles and closely interacting functionalities such as catechol, pyrogallol, 3-OH/4-oxo or 5-OH/4-oxo groups. The most common form of distortion was a very high torsion angel of ring-B, which often equilibrated around 90°. UMP2-related problems were more pronounced in the case of singlet and doublet states of flavonoids. We suspect that the correlation correction afforded by UMP2 to the flavones and flavonols we studied, may have been a bit excessive.^20,21

Our preliminary assessments of B3LYP and B2PLYP-D for the intended study revealed that they were not suitable for proper representation of the radical and diradical natures of flavonoids. The spin-density of the singlet state of flavonoids could not be studied and compared with UHF results because of the inherent nature of DFT. The unrestricted B3LYP (UB3LYP) and unrestricted B2PLYP-D (UB2PLYP-D) treatments of the singlet state of flavonoidal parent structures failed to yield their spin-densities. This results from the fact that spin-DFT will reduce to the ordinary form of DFT for species with all electrons paired and molecular geometries in the region of equilibrium geometry.^22,23 Also, we were not, in general, able to get usable information from the UB3LYP spin-density distributions of flavonoidal phenoxyl radicals. Note that we did not examine our phenoxyl radicals with UB2PLYP-D. However, the most important failure of both B3LYP and B2PLYP-D was their inability to produce acceptable equilibrium geometries for some triplet states of flavonoids. Triplet conformations of flavonoids where the Δ_2–3 π bond electrons were unpaired and which as a result would be expected to undergo distortion around that bond,^22,23 had virtually the same local configuration as their singlet counterparts. It should be noted that this particular type of triplet states did not need to be considered in later part of the study. But nevertheless, such shortcomings, as well as their relatively high computational costs ultimately cast doubt on the advisability of employing of B3LYP and B2PLYP-D for this study. See Supplementary Information for some examples and further discussion on the difficulties outlined above.

Owing to their limited performances and also in the interest of time and resource, the post-Hartree–Fock methods were totally abandoned, resorting to only UHF. Notwithstanding its natural limitations, Hartree–Fock is one of the most suitable and economical methods for a rather accurate estimation of change in enthalpy of formation.^24,25 The use of UHF gained impetus as its results were in line with the conclusions of the present study, which could be drawn from an undisputable and totally independent line of reasoning (vide infra).

3′4′-Dihydroxyflavone

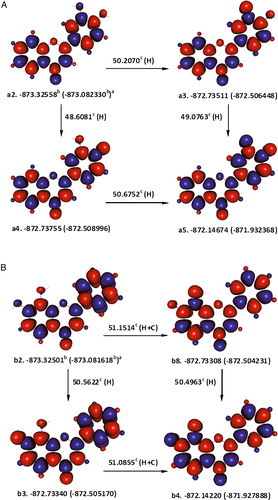
The first hydrogen atom was abstracted from 4′-OH of a2 (Δ_rH°(298 K) = 48.6081 kcal mol⁻¹) as the associated enthalpy change was lower by ca. 1.5989 kcal mol⁻¹, than that of 3′-OH's (Fig. 1A). Note that stabilization by about 5.6658 kcal mol⁻¹ could be bestowed on a4, if hydrogen bonding was established with 3′-OH (not considered throughout this study). Further abstraction of a hydrogen atom from 3-OH of 3′4′-dihydroxyflavone radical_4′-OH was accompanied with an enthalpy change of 50.6752 kcal mol⁻¹, leading to the formation of a stable quinone derivative (a5). Naturally, the net enthalpy change associated with removing two hydrogen atoms from 3′4′-dihydroxyflavone leading to the formation of its quinone derivative would be the same whatever reaction path is followed, i.e. 99.2833 kcal mol⁻¹.

Figure 1. The formation of ortho-quinone derivatives of 3′,4′-dihydroxyflavone (A) and 7,8-dihydroxyflavone (B) after the sequential abstraction of two phenolic hydrogen atoms. ^aɛ₀(ɛ₀ + H_corr), where ɛ₀ is the SCF and H_corr is the ‘thermal correction to enthalpy’; ^bHartree; ^ckcal mol⁻¹; C is the enthalpy change for interconversion of conformers; and H is the removal of a hydrogen atom; red and blue are the spin up and spin down regions, respectively.

7,8-Dihydroxyflavone

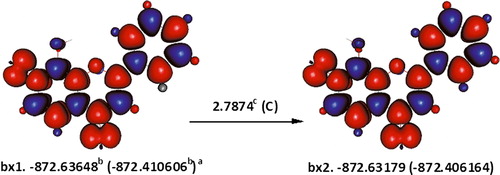
The hydrogen bonding that the 8-OH hydrogen atom forms with the heteroatom ring oxygen is weaker by 2.3074 kcal mol⁻¹, than the one it forms with 7-OH in b2 (Fig. 1B). With respect to b2, removing 7-OH hydrogen atom may appear to be slightly more favourable over 8-OH hydrogen atom, due to the hydrogen bonding of the later with the ring oxygen. The strength of this hydrogen bonding was estimated to be ca. 2.7874 kcal mol⁻¹, from the energy difference between the quartet conformations, bx1 and bx2, in which 8-OH hydrogen atom is only able to form a hydrogen bond with the ring oxygen and not the radical oxygen (7-O) (Fig. 2). Once correcting for the aforementioned hydrogen bonding in b2, the enthalpy change for abstracting the 8-OH hydrogen atom adjusted to 48.3640 kcal mol⁻¹. Removing the phenolic hydrogen atom of b8 involves an enthalpy change of 50.4963 kcal mol⁻¹.

Figure 2. Estimating the hydrogen bonding between 8-OH and the ring oxygen in 7,8-dihydroxyflavone using higher spin states. The orientation of the localized electron cloud on 7-O does not allow an effective overlap with the hydrogen atom of 8-OH. ^aɛ₀(ɛ₀ + H_corr), where ɛ₀ is the SCF and H_corr is the ‘thermal correction to enthalpy’; ^bHartree; ^ckcal mol⁻¹; C is the enthalpy change for interconversion of conformers; red and blue are the spin up and spin down regions, respectively.

3,7-Dihydroxyflavone

Obtaining a convergence for singlet state conformations of 3,7-dihydroxyflavone, in which 3-OH is not hydrogen bonded to 4-oxo group, proved to be extremely difficult unless ring-B was positioned perpendicular to the rest of the molecule. In order to avoid such drastic structural changes, the abstraction of hydrogen atoms from 3,7-dihydroxyflavone and the other flavonols studied was started from the respective ground state hydrogen-bonded conformers. c1, c2, and c3 in Fig. 3 are hydrogen-bonded conformers of 3,7-dihydroxyflavone, which we were able to identify. They differ in the position of 7-OH and/or spin-density distribution. Unfortunately, we could not obtain a convergence for the conformer, having the 7-OH pointing upwards and a spin-density distribution similar to that of c2's. If c1 and c3 are compared, both SCF and ɛ₀ + H_corr values would indicate that, in the lowest energy conformation, the hydrogen atom of 7-OH may be pointing upwards. A similar comparison between c1 and c2 would favour the former, on the basis of SCF, or the later, on the basis of ɛ₀ + H_corr values, as the spin-density distribution conferring lower energy. Therefore, both c2 and c3 served as two alternative lowest energy conformations of 3,7-dihydroxyflavone.

Figure 3. Hypothetical pathways for the abstraction of two hydrogen atoms from 3,7-dihydroxyflavone, leading to the formation of a relatively stable extended conjugated product (c8). In the singlet state conformers, c2 and c3, the abstraction of the 3-OH hydrogen atom may be hindered due to its strong hydrogen bond with the 4-oxo group. Undergoing internal rearrangements may enable breaking this hydrogen bond as in, for instance, c9. ^aɛ₀(ɛ₀ + H_corr), where ɛ₀ is the SCF and H_corr is the ‘thermal correction to enthalpy’; ^bHartree; ^ckcal mol⁻¹; C is the enthalpy change for interconversion of conformers; H is the removal of a hydrogen atom; red and blue are the spin up and spin down regions, respectively.

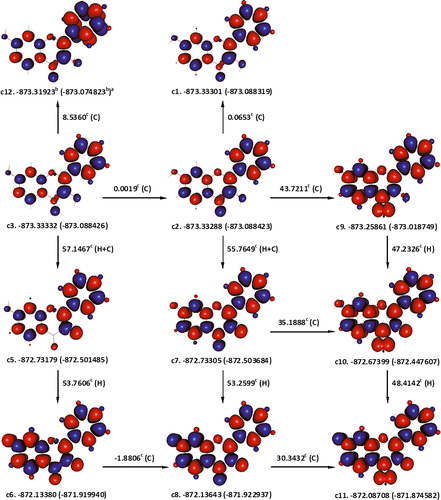
Fig. 3 illustrates hypothetical steps for the abstraction of two hydrogen atoms from 3,7-dihydroxyflavone. Starting from c2, the total apparent enthalpy change accompanying the abstraction of two hydrogen atoms would be 109.0248 kcal mol⁻¹ ((55.7649 + 53.2599) kcal mol⁻¹) and starting from c3, 109.0267 kcal mol⁻¹ ((57.1467 + 53.7606–1.8806) kcal mol⁻¹). Both total enthalpy changes, however, include the works done to break the hydrogen bond between the 3-OH hydrogen atom and 4-oxo group, in addition to the works done to dissociate the O–H bond. The strength of the hydrogen bonding between the 3-OH and 4-oxo groups was estimated by considering the abstraction of a hydrogen atom from 3-OH of a triplet state of 3,7-dihydroxyflavone, c9, which entails an enthalpy change of 47.2326 kcal mol⁻¹. The strength of the hydrogen bond in question would thus be 8.5323 kcal mol⁻¹ (55.7649–47.2326). Expectedly, a difference of 8.5323 kcal mol⁻¹ also exists between the enthalpy changes accompanying the formation of the triplet state c9 from c2 (43.7211 kcal mol⁻¹) on one hand side, and the quartet state c10 from c6 (35.1888 kcal mol⁻¹), on the other. Consequently, 47.2326 kcal mol⁻¹ was taken as a better estimation for the enthalpy change associated with the removal of a hydrogen atom from 3-OH of 3,7-dihydroxyflavone. For 3,7-dihydroxyflavone, it was also possible to locate the conformer c12, in which the hydrogen bond between 3-OH and 4-oxo groups is disrupted. Using c12, the hydrogen bonding in question was estimated to be 8.5360 kcal mol⁻¹, in an excellent agreement with the previous one. Unfortunately, we could not manage to locate non-hydrogen-bonded singlet-state conformers similar to c12, for the other flavonols studied.

3,4′-Dihydroxyflavone

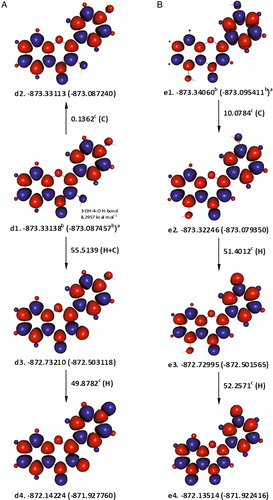
In 3,4′-dihydroxyflavone, the relative position of 4′-OH may not have a significant effect on energy as the enthalpy difference between d1 and d2, depicted in Fig. 4A, is only 0.1362 kcal mol⁻¹. The strength of the hydrogen bond between 3-OH and 4-oxo groups was estimated to be around 8.2957 kcal mol⁻¹, using higher spin state conformations in the same way as described for 3,7-dihydroxyflavone. Assuming that the first hydrogen atom is abstracted from 3-OH, the corrected enthalpy change, accompanying this process would be around 47.2182 kcal mol⁻¹. The resulting 3,4′-dihydroxyflavone radical_3-OH (d3) can lose a second hydrogen atom from its 4′-OH, with an associated enthalpy change of 49.8782 kcal mol⁻¹, yielding the extended quinone, d4.

Figure 4. Abstraction of two hydrogen atoms from 3,4′-dihydroxyflavone (A) and 3′,5-dihydroxyflavone (B). Subtracting the work done to break the hydrogen bond in the former is mandatory to justify the fact that it is a potent radical scavenger. ^aɛ₀(ɛ₀ + H_corr), where ɛ₀ is the SCF and H_corr is the ‘thermal correction to enthalpy’; ^bHartree; ^ckcal mol⁻¹; C is the enthalpy change for interconversion of conformers; H is the removal of a hydrogen atom; red and blue are the spin up and spin down regions, respectively.

3′,5-Dihydroxyflavone

As shown in Fig. 4B, rotating 5-OH in e1 to the opposite side abolishes its hydrogen bonding with 4-oxo group, and increases energy by 10.0784 kcal mol⁻¹. Alternatively, higher spin state conformers could be employed, to the same effect, as demonstrated for 3,7-dihydroxyflavone above (not shown). In e2, the homolytic dissociation of 3′-OH, which is associated with an enthalpy change of ca. 51.4012 kcal mol⁻¹, may slightly be flavored over that of 5-OH (roughly by about 0.8 kcal mol⁻¹). If a further abstraction of a hydrogen atom was to take place from 5-OH of 3′,5-dihydroxyflavone radical_3′-OH (e3), it may proceed accompanied with an enthalpy change of ca. 52.2571 kcal mol⁻¹, giving rise to an apparently extended quinone derivative.

4′,7-Dihydroxyflavone

The ground state conformation of 4′,7-dihydroxyflavone is f1 shown in Fig. 5A. The ring-B phenolic group may donate its hydrogen atom with a relative ease compared with that of ring-A's. As in the case of 3′,5-dihydroxyflavone, abstraction of a second hydrogen atom from 4′,7-dihydroxyflavone radical_4′-OH (f2) may give rise to a product with an extended conjugation (f3). In this case, however, f3 is more stable in its triplet state.

Figure 5. The hypothetical formation of the biradical derivatives of 4′,7-dihydroxyflavone (A) and 3,3′-dihydroxyflavone (B). The triplet state conformations of the biradicals (f3 and g3) possess less energy than the corresponding singlet forms. Note that in g4, C2, and C1′ have acquired similar spin-densities, forcing ring-B to twist by ca. 65°, relative to ring-C. ^aɛ₀(ɛ₀ + H_corr), where ɛ₀ is the SCF and H_corr is the ‘termal correction to enthalpy’; ^bHartree; ^ckcal mol⁻¹; C is the enthalpy change for interconversion of conformers; H is the removal of a hydrogen atom; red and blue are the spin up and spin down regions, respectively.

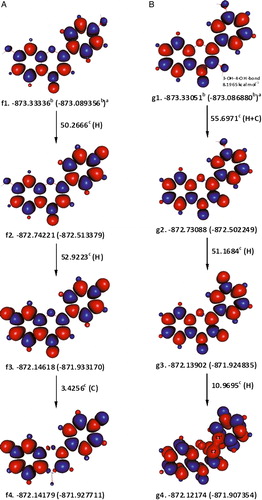
3,3′-Dihydroxyflavone

Rotating the position of 3′-OH in the conformer of 3,3′-dihydroxyflavone, g1 shown in Fig. 5B, changing its spin-density distribution pattern to the one similar to c1's (Fig. 3), or both result in a slight increase in energy. The hydrogen bonding between the 3-OH and 4-oxo groups was approximated to be around 8.1965 kcal mol⁻¹, using higher spin state conformations as described earlier. Consequently, the first hydrogen atom was removed from 3-OH with an associated enthalpy change of 47.5006 kcal mol⁻¹. Once again, abstraction of the 3′-OH hydrogen atom of 3,3′-dihydroxyflavone radical_3-OH (g2) produces a biradical, which is more stable in its triplet state (g3). Transforming g3 into the lowest energy singlet state (g4), requires the disconjugation of ring-B from the rest of the molecule, at the expense of 10.9695 kcal mol⁻¹.

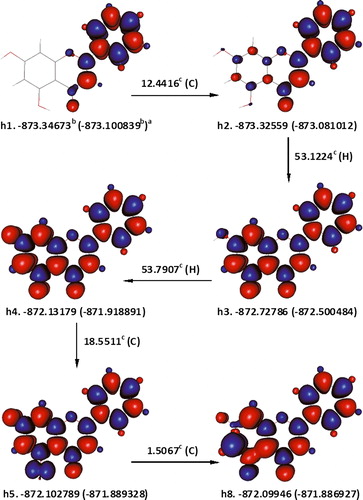
5,7-Dihydroxyflavone

h1 is the most stable conformation of 5,7-dihydroxyflavone and h2 is another conformation which is ca. 12.4416 kcal mol⁻¹ higher in energy (Fig. 6). The later was used to study the homolytic dissociations of 5,7-dihydroxyflavone as none of its hydroxyl groups is engaged in a hydrogen bonding. The first hydrogen atom was removed from 5-OH (53.1224 kcal mol⁻¹), since it is slightly weakly bound compared with that of 7-OH's. Abstraction of 7-OH hydrogen atom from 5,7-dihydroxyflavone radical_5-OH (h3), produces a triplet state meta-quinone derivative (h4), which is much more stable than its singlet counterparts.

Figure 6. The formation of a meta-quinone from 5,7-dihydroxyflavone. The triplet state biradical (h4) is considerably more stable than any of its corresponding singlet states. ^aɛ₀(ɛ₀ + H_corr), where ɛ₀ is the SCF and H_corr is the ‘thermal correction to enthalpy’; ^bHartree; ^ckcal mol⁻¹; C is the enthalpy change for interconversion of conformers; H is the removal of a hydrogen atom; red and blue are the spin up and spin down regions, respectively.

Discussion

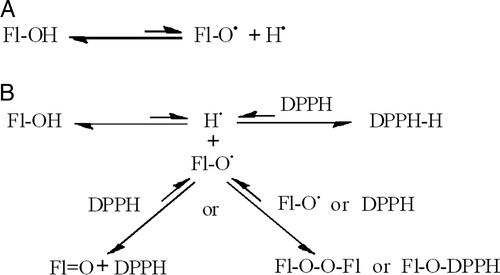
Our working reaction model for the radical-scavenging activities of flavonoids, shown in Fig. 7, stipulates an initial equilibrium homolytic dissociation of susceptible hydroxyl groups, which produces hydrogen atoms and phenoxyl radical derivatives of flavonoids (Fig. 7A). In all likelihood, only a very small proportion of flavonoid molecules may undergo homolytic dissociation, the extent of which would largely be dictated by the inherent nature of the flavonoids as well as the medium's capacity to support flavonoidal radicals and conformational changes. The addition of an external radical such as DPPH leads to the depletion of the hydrogen atoms and shifts the equilibrium towards the dissociation of the flavonoid. Yet, the rate of depletion of hydrogen atoms should be paralleled with the termination of the phenoxyl radicals if further appreciable dissociation is to occur (Fig. 7B).³ This model is in line with the conclusion of Wright et al.²⁶ that hydrogen atom transfer may be the principal mechanism by which the majority of the antioxidants they studied, which included a variety of phenolic derivatives, worked. It is also in concord with the conclusions of Mikulski et al.²⁷ that in both gaseous phase and water hydrogen atom transfer may outweigh competing reaction mechanisms, and also antioxidant potency strongly depended on structural factors and type of medium. Hydrogen atom transfer mechanism may also be biologically relevant.²⁸ Moreover, our reaction model is also in good agreement with reports indicating that kinetic solvent effects on hydroxylic hydrogen atom abstractions are generally independent of the nature of the abstracting radical.²⁹ It is also accommodative of inter-/intra-molecular hydrogen bonding in polyphonols³⁰ and other miscellaneous processes³¹ known to influence the radical-scavenging activities of flavonoids.

Figure 7. The equilibrium homolytic dissociation of flavonoids (A) and their equilibrium reactions with free radicals such as DPPH (B).

As can be gathered from Figs. 1–6, for all the flavonoids considered in this study, the process of abstracting two hydroxylic hydrogen atoms starts from the respective hydroquinone structures, which are least stabilized by hydrogen-bonding, and finishes with singlet state quinone or quinone-like derivatives. We assume that other practical termination mechanisms including dimerization and disproportionation^32,33 may not be significant in the reactions of these flavonoids with DPPH. From a series of preliminary results, it was concluded that, hydrogen bonding influencing a given hydroxyl group need to be abolished first or, at least, significantly minimized before calculating the enthalpy of reaction for the removal of its hydrogen atom. Otherwise, the apparent calculated enthalpy of reaction will include the enthalpy for breaking the hydrogen bond on top of the actual enthalpy for the homolytic bond dissociation.^34,35 This approach partly stemmed from the known positive contribution of certain hydroxyl groups, such as 3-OH, to the radical-scavenging activities of flavonoids, which did not correlate well with calculated thermodynamic quantities, as long as hydrogen bonds were not excluded. It should also be taken into account that the success of comparison across a similar type of change (e.g. bond dissociation), would depend among other things, on the selection of equivalent conformers. For instance, if a hydrogen bond is found in the parent structure, the same should be conserved in the radical counterpart, in order to be able to use this pair for comparison. Otherwise, once again the determination of accurate enthalpies of reactions will be hindered by the incorporation of enthalpies associated with conformational difference.

On account of the fact all the eight flavonoids studied exhibited diradical nature, triplet and quartet multiplicities were routinely analysed, to assess the possible participation of such excited states of flavonoids in their radical-scavenging activities. This exercise proved to be highly relevant and provided a new and more complete picture of the molecular phenomena which are very likely to occur during the radical-scavenging reactions of flavonoids. However, with the main exception of flavonols, the explicit consideration of triplet and quartet conformations was not as such required in the determination of the net enthalpy changes accompanying the abstraction of hydrogen atoms from flavonoids. In the case of flavonols, the isolation of the rather strong hydrogen bonding between 3-OH and 4-oxo groups was only made possible owing to the analyses of higher spin states. After the exclusion of this hydrogen bonding that was on average over 8 kcal mol⁻¹, the enthalpy change for the abstraction of the 3-OH hydrogen atom dropped to ca. 47 kcal mol⁻¹. This trend is in line with our pervious assertion, that in the presence of a 2–3 double bond, the abstraction of 3-OH hydrogen atom may require a relatively low-energy change.³ Along the same lines, this trend is also in an excellent agreement with our finding that the abstraction of the 3-OH hydrogen atom of 2-phenyl-4H-chromene-3,7-diol (where there is no hydrogen bonding) may only impose an enthalpy change of 39.7395 kcal mol⁻¹.

Customarily, what is regarded as the driving force behind the excellent hydrogen donating ability of catecholic hydroxyl groups, is the hydrogen bonding in the phenoxyl radical.^5,30 What seems to be often overlooked, however, is the fact that the same hydrogen bonding would be responsible for stabilizing the initial parent compound, ultimately cancelling out any net effect. Also, catechol groups, for instance, are known to form relatively stable ortho-quinones after losing a second hydrogen atom from their pheoxyl radicals that they form when they donate a hydrogen atom.³³ This, however, would necessitate breaking the hydrogen bonding that was stabilizing the phenoxyl radical. This in turn means that the energy advantage gained through the formation or strengthening of a hydrogen bond during the abstraction of the first hydrogen atom would be lost during the abstraction of the second. Therefore, the underpinning mechanism for the reactivity of catechol and related functional groups, should lay elsewhere.

To elaborate on the preceding argument let us consider the sequential abstraction of two hydrogen atoms from a6, a hydrogen bonded conformer of 3′,4′-dihydroxyflavone (Fig. 8). The first hydrogen atom is removed from 4′-OH with an enthalpy change of 47.2998 kcal mol⁻¹, which is ca. 1.3083 kcal mol⁻¹ lower than the enthalpy change for the corresponding process in a2 (Fig. 1A). Removing the second hydrogen atom from 3′-OH of the resulting 3′4′-dihydroxyflavone radical_4′-OH (a7) entails an enthalpy change of 56.3409 kcal mol⁻¹. The later obviously includes the work done to break a hydrogen bonding with the radical oxygen atom (4′O) and is consequently ca. 5.6657 kcal mol⁻¹ higher than the enthalpy change for the same process in a4. Accordingly, unlike a2, which donates two hydrogen atoms, with a total enthalpy change of only 99.2833 kcal mol⁻¹, a6 needs an extra 4.3574 kcal mol⁻¹ to the same effect. The fact that the total enthalpy change for abstracting a pair of hydrogen atoms from a6 is 103.6407 kcal mol⁻¹ reflects that hydrogen bonding cannot benefit radical formation at the end of the day. This increase in total enthalpy change can be traced back to the stabilization of 4.3574 kcal mol⁻¹ conferred to a6 by the hydrogen bonding in its catechol group.

Figure 8. Illustration for the abstraction of two phenolic hydrogen atoms from a hydrogen-bonded conformer of 3′,4′-dihydroxyflavone. ^aɛ₀(ɛ₀ + H_corr), where ɛ₀ is the SCF and H_corr is the ‘thermal correction to enthalpy’; ^bHartree; ^ckcal mol⁻¹; C is the changes in enthalpy ΔH°(298 K) associated with interconversion of conformers; H is the removal of a hydrogen atom; red and blue are the spin up and spin down regions, respectively.

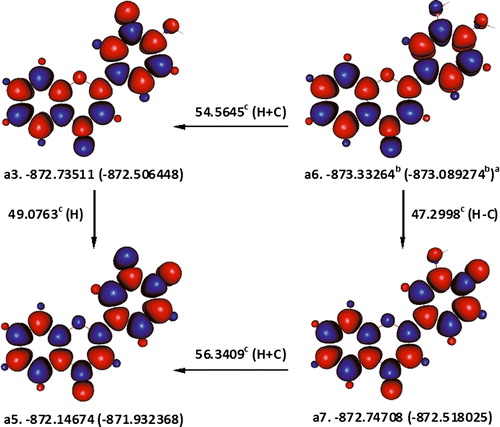
A slightly different way of looking at the same example is to account for the better stability of a7 as compared with a4. Hydrogen bonding has stabilized a4 by ca. 5.6658 kcal mol⁻¹. Only ca. 1.3083 kcal mol⁻¹ of this 5.6658 kcal mol⁻¹ was acquired as a result of the formation of a new radical centre at 4′O, while the remaining 4.3574 kcal mol⁻¹ was already present in the parent structure a6. Such an increase in the energy of the hydrogen bonding in phenoxyl radicals, may be what is perhaps alleged to be responsible for enhancing the abstraction of a hydrogen atom from catechols.³⁰ And there can be little doubt that this would be of consequence if the whole process involved the removal of only one hydrogen atom. However, if the hydrogen atom involved in the hydrogen bonding is to be removed, it will depart together with any stabilization it was conferring. Hence, the total enthalpy change associated with the removal of two hydrogen from a6 (103.6407 kcal mol⁻¹) will not be altered in any way, due to a transient energy gain or loss originating from the formation of a hydrogen bond or otherwise.

A novel correlation between the enthalpy of reaction (Δ_r H°(298 K)) for hydrogen atom abstraction and the radical-scavenging activities of flavonoids

In most of the previous studies involving the thermodynamics of the radical-scavenging activities of flavonoids, it is only the removal of the first phenolic hydrogen atom that has been considered.³⁶ In the present study, however, the removal of the second phenolic hydrogen atom was also studied. Table 1 presents the reported DPPH scavenging activities of the eight dihydroxyflavonoids studied together with enthalpy changes resulting from the homolytic dissociations of their hydroxyl groups. At least for the sake of argument, singlet-state quinones or quinone-like products will be taken as a common end point of the abstraction of two hydrogen atoms from the flavonoids. As is evident form Table 1, the sums of the enthalpies of reaction for the abstraction of the first and second hydrogen atoms, were significantly below 104 kcal mol⁻¹, for flavonoids that have been reported to be potent radical scavengers. However, the sums tend to be close to or greater than 104 kcal mol⁻¹, for those flavonoids which have been reported to be weak radical scavengers. This value is very much close to the experimental enthalpy of the homolytic dissociation of molecular hydrogen (H₂), 104.206 ± 0.003 kcal mol⁻¹.³⁷ Thus it was suspected that, for flavonoids and related polyphenols to act as excellent radical scavengers, they should be able to donate a pair of hydrogen atoms with a total enthalpy of reaction, which does not exceed the enthalpy of the homolytic dissociation of H₂. In our previous study, we have come across a similar type of cut-off point for heat of formation, which we then used as a primary guide for qualitatively predicting radical-scavenging activity.³

Table 1. Enthalpy changes associated with abstraction of two hydrogen atoms from the flavonoids studied together with the reported activities of the flavonoids in DPPH scavenging assays.

Flavonoid	ΔiH°(298 K) kcal mol^−1			∑ ΔiH°(298 K) kcal mol^−1	DPPH-scavenging activity
	H1	H2	C
3′4′-Dihydroxyflavone	48.6081	50.6752		99.2833	Active^Citation6,Citation7
7,8-Dihydroxyflavone	48.3640	50.4963		98.8603	Active^Citation3
3,7-Dihydroxyflavone	47.2326	53.2599		100.4925	Active^Citation3,Citation6,Citation8
	48.6106	53.7606	−1.8806	100.4906
3,4′-Dihydroxyflavone	47.2182	49.8782		97.0964	Active^Citation6
3′,5-Dihydroxyflavone	51.4012	52.2571		103.6583	Inactive^Citation7
4′,7-Dihydroxyflavone	50.2666	52.9223	3.4256	106.6145	Inactive^Citation7
3,3′-Dihydroxyflavone	47.5006	51.1684	10.9695	109.6385	Inactive^Citation6
5,7-Dihydroxyflavone	53.1224	53.7907	18.5511	125.4642	Inactive^Citation3,Citation6,Citation7

Δ_iH°(298 K): enthalpy change accompanying process i at 25°C, where i stands for H1: abstraction of the first hydroxylic hydrogen atom; H2: abstraction of the second hydroxylic hydrogen atom; and C: conformational change.

A thermochemical deduction of the correlation between the radical-scavenging activity of flavonoids and the homolytic dissociation of H₂

The proposed relationship between the radical-scavenging activity of flavonoids and the homolytic dissociation of H₂ can actually be directly derived from the stoichiometric relationship shown in Reaction 1, by appealing to an equilibrium dynamics or alternatively, chemical coupling. First let us take an ortho-dihydroxyflavone for the sake of convenience. Also for convenience, its reaction with DPPH would be considered.

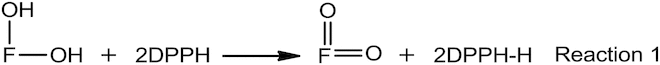
As shown in Reaction 1, the ortho-dihydroxyflavone (F–OH), will give up two hydrogen atoms that will reduce two DPPH molecules and give rise to an ortho-quinone derivative (F=O). Now let us expand Reaction 1 with hypothetical elementary reactions.

Reaction 2 is the abstraction of a hydrogen atom (H^•) from the flavonoid. Reaction 3 is the abstraction of a second hydrogen atom from the phenoxyl radical of the flavonoid formed in Reaction 2. Reaction 4 shows that the hydrogen atoms formed in Reactions 2 and 3 are in equilibrium with atmospheric hydrogen molecules (H₂) which itself is, of course, in equilibrium with hydrogen molecules in the reaction medium (not shown here). Reaction 5 is obviously the reduction of DPPH.

We can add together Reactions 2 and 3 to get Reaction 2-3.

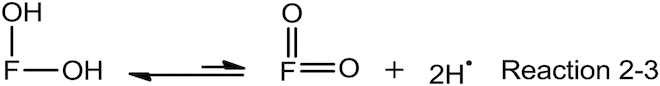
We can also add Reaction 4 to Reaction 2-3, there by establishing an equilibrium involving the dihydroxyflavone, its ortho-quinone derivative and atmospheric molecular hydrogen (Reaction 2-3-4).

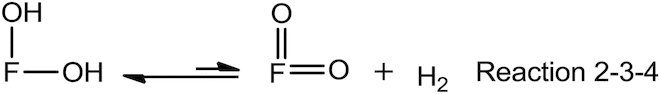
Therefore, the elementary reactions of Reaction 1 can be rewritten as the following:

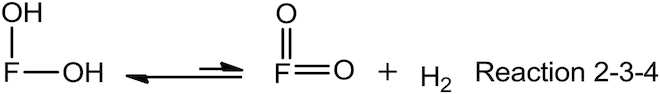
The enthalpy of Reaction 5 is estimated to be −104.8794 kcal mol⁻¹, according to Eq. 2. Note that the absolute value of this enthalpy change is quite close to the experimental enthalpy of the homolytic dissociation of molecular hydrogen (H₂)!³⁷ Reaction 5 may, in any case, be anticipated to be fast and thus non-rate-limiting step. On the contrary, let us assume that Reaction 2-3-4 is slow and rate limiting.

The enthalpy of Reaction 2-3-4 can be calculated by partitioning it into Reaction 2-3 and Reaction 4, for which enthalpies of reaction are either known or can be determined readily (Hess's Law). 3

The enthalpy of Reaction 2-3 may be calculated according to Eq. (2) and is designated here as Q. The experimental value for the enthalpy of Reaction 4 is −104.206 ± 0.003 kcal mol⁻¹ since it is simply the reverse of the homolytic reaction of molecular hydrogen.³⁷ In other words, the enthalpy of Reaction 4 is the energy released up on the fusion of two hydrogen atoms.

The enthalpy of Reaction 2-3-4 is thus:

It follows that, for Reaction 2-3-4 to be exothermic, Q should be less than 104.206 kcal mol⁻¹. Since, in Reaction 2-3-4, two products are formed from one reactant, entropy may be expected to favour the forward reaction. Therefore, if Reaction 2-3-4 and, by extension, Reaction 1, can go forward or not may only depend on Q. On the basis of the above deduction and in line with the theoretical computation results already discussed, we may conclude that, a flavonoid can act as a hydrogen atom donor, if and only if, two hydrogen atoms can be extracted with an enthalpy of reaction that is less than the enthalpy of the homolytic dissociation of H₂ at a given temperature. The above conclusion implies that, a successful cycle of radical-scavenging reaction occurring through the transfer of hydrogen atoms may require the transfer of a pair of hydrogen atoms. Perusal of literature would reveal that such requisite may not be restricted to flavonoid antioxidants. As well, the general applicability of this inference, to flavonoids and related polyphenols, which oxidize to products different from quinones (e.g. dimers, oligomers, cyclic products, or their combinations) and, by and large, other hydrogen donating antioxidants can readily be shown. In such compounds, the preceding argument can be pursued to reach at Reaction 6, which is analogous to Reaction 2-3-4. Reaction 6 will then be split into Reaction 6a and Reaction 4, in order to calculate its enthalpy, just as in the case of the dihydroxyflavone example. We can then proceed to prove that the enthalpy of Reaction 6 is equal to the sum of the enthalpy of Reaction 6a and −104.206 kcal mol⁻¹. In the proceeding section, an attempt will be made to highlight the relevance of our proposed hydrogen-pair transfer (HPT) mechanism to the general discussion of antioxidants by considering a few prototype examples.

Applicability of the hydrogen-pair transfer mechanism to other antioxidants

Chalcones have been shown to exhibit excellent radical-scavenging activities due to their ability to form cyclic products, in addition to the usual phenolic attributes.^38,39 In the dihydrochalcone phloretin, 2,6-dihydroxyacetophenone is demonstratively the essential pharmacophore.⁴⁰ We have estimated the total enthalpy change accompanying the cyclization 2,6-dihydroxyacetophenone to 4-hydroxybenzofuran-3(2H)-one, after losing two hydrogen atoms from the 6-OH and methyl groups, to be ca. 98.8428 kcal mol⁻¹. Similarly, the conversion of ascorbic acid into dehydroascorbic acid may entail an enthalpy change of 99.4577 kcal mol⁻¹. Furthermore, the biological antioxidant glutathione may apparently owe its antioxidant property to the fact that it dimerizes into glutathione disulfide, with an enthalpy change of only 97.6104 kcal mol⁻¹.

Conclusion

The radical-scavenging activities of flavonoids and possibly other antioxidants, may originate from their superior abilities to donate a pair of hydrogen atoms relative to H₂. Thus, by considering the enthalpy of the homolytic dissociation of H₂, 104.206 kcal mol⁻¹, as the benchmark for radical-scavenging reactions, it might be possible to come up with a standard scale for hydrogen atom donating abilities of phenolic and other antioxidants. Obviously, as the process of abstracting two hydrogen atoms from an antioxidant proceeds with a lower enthalpy change, a more potent radical-scavenging activity may be prompted. Furthermore, in combination with kinetic data, this relationship may assist in elucidating inclusive quantitative structure–activity relationships (QSAR).

We have used gas phase computations and essentially a hydrogen atom transfer mechanism to justify a far reaching conclusion for antioxidants. Undoubtedly, this preliminary study could be refined further. Nevertheless, it has shed new light on the fact that thermodynamic barriers may be the major factors influencing the radical-scavenging reactions of antioxidants. The approach followed in this study could be applied to investigate complex systems such as reactions in solutions and other media, to precisely account for various questions surrounding antioxidants. Unanswered questions encompassing the limit to antioxidant activity,⁴¹ on the one end of the spectrum, to the induction of prooxidation, on the other, may very well be explained with a careful consideration of thermodynamical relationships.

Naturally, thermodynamics will dictate the extent of reactions while kinetics will have its say on how fast they occur, often independent of each other. In our view, however, what seems to hinder the understanding of antioxidants is the obscure or totally absent demarcation between these two, in most interpretation of results and discussions in the literature. A case in point, perhaps is the rather widespread confusion between what are commonly referred to as BDE and change in heat of formation (referred to as enthalpy change in this report). In relation to this, our conclusion regarding the thermodynamical basis of the radical scavenging activity of phenolic and related antioxidants is in sharp contradiction with the common but erroneous use of BDE to measure the direction of hydrogen atom transfer reactions.

Unlike the enthalpy changes calculated in this study, both experimental and theoretical BDEs are likely to incorporate the activation energy, making them more suitable for kinetic investigations. Hartee–Fock calculations ‘normally’ produce energy changes which are way below experimental BDE values. Among other things, this has resulted in excessive dependence on relatively expensive post Hartree–Fock methods, which may not always meet their purposes and the results of which should be considered with caution.^20,22 And needless to say that this may have fed a somewhat self-perpetuating cycle of failure in adequately characterizing antioxidant activity with theoretical computations. If properly implemented, however, Hartree–Fock is even capable of satisfactorily reproducing experimental BDE values of antioxidants, as was exemplified in a diffusion Monte Carlo study.⁴² Our own findings on the usability of Hartree–Fock for the calculation of BDE will be reported separately in our subsequent publication. Be that as it may, we would like to point out, however, that the common practice of studying the transfer of only one hydrogen atom from antioxidants ought to be revised, as it fits better the propagation phase of radical reactions than it actually does termination.

Aside from computational approaches, admittedly, drawing a fine line between the thermodynamic and kinetic aspects of reactions, which are in turn dictated by internal (structural) and external (temperature, pressure, medium, pH, etc.) factors, may be far from easy, as far as the radical scavenging reactions of phenols and related compounds are concerned.⁴³ As noted by anonymous Referees, antioxidants may also work through different mechanisms depending on the type of medium. We would like to stress nevertheless that the extent of reactions, which for our case is the net transfer of hydrogen atoms, should in principle be independent of anything else but the relative potential energies of the reactants and products. Thus, ideally speaking, even though rates and mechanisms are largely dictated by reaction conditions, the net energy gain or loss by the system in removing a hydrogen atom in any manner (as an atom or the electron and proton sequentially, in no particular order) should be the same no matter what.⁴⁴

Acknowledgements

This work was supported by UWSIPRS scholarship and the NCI National Facility at the ANU. Computational and storage resources used were provided by Intersect Australia Ltd.

Funding

The funding was supported by UWSIPRS, University of Western Sydney International Postgraduate Research Scholarships and NCI National Facility at the Australian National University (ANU).