Ethical economics and cost–effectiveness analysis: is it ethical to ignore opportunity costs?

Cost–effectiveness analysis (CEA) has been adopted as a method for informing healthcare decision-makers about alternative uses of healthcare resources. By comparing the incremental costs and effects of a new intervention relative to the existing approach to dealing with the same patients, decision-makers seek to choose those investments that lead to the production of maximum health gain from available healthcare resources. The analytic tool of CEA is the incremental cost–effectiveness ratio (ICER) obtained by the incremental cost of the new program divided by the incremental effects. Using a theoretic model based on assumptions of perfect divisibility and constant returns to scale in all programs, Weinstein and Zeckhauser derived the following decision rules, both of which produce maximum health gain from available resources [1]:

•	The league table rule: select programs in ascending order of ICER (i.e., project with lowest ICER first) until available resources are exhausted
•	The threshold ICER rule: select programs with an ICER less than or equal to λ, the shadow price of available resources (i.e., the budget)

Because ICERs are not available for all healthcare interventions, comprehensive league tables are not available and the first of these decision-rules is therefore not feasible [2,3]. Instead, the threshold rule has provided the basis for institutional approaches to informing healthcare decision makers (e.g., Commonwealth of Australia 1995, Ontario Ministry of Health 1994, National Institute for Clinical Excellence 2001). Determination of the shadow price of resources has also proved to be elusive, since this implies the λ value is determined endogenously and hence will vary between decision settings and time points as the range of possible interventions and budget allocations change. In response to this limitation, an alternative approach is used for determining the λ value; λ is assumed to be given by the decision-maker’s maximum willingness to pay (WTP) per additional unit health gain (e.g., quality-adjusted life year [QALY]). However, based on empiric evidence of differences in WTP for gains and willingness to accept (WTA) losses at the individual level, O’Brien and colleagues proposed that a different λ value may apply in situations where a new intervention is less costly but less effective than the current intervention to the more traditional decision problem of the new intervention being more effective but more costly than the current intervention. In terms of the cost–effectiveness (CE) plane (Figure 1) this implies a ‘kink’ in the decision-maker’s threshold at the origin with all interventions falling to the north and west of the kinked line representing inefficient use of resources and those to the south and east of the kinked line representing efficient use of resources [4].

Kent and colleagues also discuss the evaluation and use of less effective and less expensive medical interventions in the context of the development of new interventions [5]. They argue that ‘from a societal perspective…the fundamental goal of innovation should not be restricted to improvement on the best available option. Rather, in a setting in which some do not have access to the ‘best’, more aggregate health benefits will result from innovations that allow more widespread diffusion of effective interventions, albeit not the best one. This strategy is particular germane in resource-limited settings’. Kent and colleagues argue that determining the acceptance of new, less expensive and less effective medical interventions should be subject to a different decision rule than the one used to determine the acceptance of new interventions that are more effective and more expensive [5]. They suggest a new concept of the maximally acceptable difference (MAD). The MAD is a level of inferiority beyond which a new, less effective and less expensive agent would no longer be attractive when compared with the best standard. This approach is justified based on the same argument used by O’Brien and colleagues [4], that ‘individuals are reluctant to relinquish entitlements to better medical interventions for less effective, cost-saving ones, even if the resultant savings would enable them to purchase additional items of equal or greater value’.

Dowie argued that having a different ICER threshold in the South West (SW) quadrant (new intervention is less effective but less costly) and the North East (NE) quadrant (new intervention is more effective but more costly) of the CE plane cannot be justified [6]. In particular, he argues that ‘the basic case for applying the same decision rule in the SW quadrant as well as the NE one…is the simple ethical argument based on the same opportunity cost reasoning used in the NE quadrant’ [6]. In other words, whatever λ value is used to determine whether to adopt more costly/more effective interventions, the same value must be used to determine whether to cancel less costly/less effective interventions if available resources are to be used in ways that maximize total health gain (i.e., efficiently). In this article we show that although Dowie’s diagnosis of the problem is correct, his proposed solution does not lead to the efficient use of healthcare resources. We then show how the use of an alternative decision rule is consistent with both Dowie’s ethical concerns as well as improvements in the efficiency of resource use [7,8]. The proposed solution is illustrated using a decision-making (DM) plane [9].

Figure 1. The cost-effectiveness plane and its ethical implications.

(Note that area A is not bounded to the South.) QALY: Quality-adjusted life year.

Figure 2. The ethical quadrant of the decision making plane.

The problem

Dowie starts from a societal objective of maximizing health outcomes (e.g., QALYs) subject to a healthcare resource constraint [6]. In the absence of the resource constraint it would be unethical as well as inefficient to consider adopting interventions that produce less QALYs but at a lower cost (i.e., the SW quadrant of the CE plane in (Figure 1)) simply because resources are not scarce and hence there is no alternative use for resources released by adopting a less effective intervention. However, where resources are constrained, making choices in favor of one intervention over another involves opportunity cost considerations. A new intervention that increases QALYs but requires additional resources (i.e., in the NE quadrant of the CE plane) represents an efficient use of resources only if the additional QALYs generated by the intervention exceed the opportunity cost in terms of the QALYs forgone from the intervention or interventions that will need to be cancelled to free up enough resources to support the new intervention. The use of the same decision rule in both quadrants (i.e., NE and SW) will allow us to release resources by cancelling less efficient programs (i.e., adopting programs in the SW quadrant) and using those resources to fund more efficient programs in the NE quadrant [6]. The decision rule that Dowie advocates is the threshold ICER rule derived by Weinstein and Zeckhauser. However, there are several important implications of this theoretic approach [7–9]. In particular, the threshold ICER is a function of, inter alia, the size of the budget. Changes to the budget will lead to corresponding changes to the threshold ICER required to maximize health gains [4]. Moreover, as new programs are funded and others replaced, the identification of the last program funded changes, implying that the threshold ICER also changes [10]. The unrealistic nature of the Weinstein–Zeckhauser theoretic assumptions concerning perfect divisibility and constant returns to scale of all interventions mean that application of the threshold ICER approach need not be compatible with maximizing health gain [7–9]. Finally, even if one is willing to accept these theoretic assumptions, the threshold ICER cannot be determined because information on the costs and effects of all programs is incomplete [2,11,12].

Dowie notes that ‘we have little or no knowledge about from where the extra resources for new (interventions) are to be taken – and therefore cannot establish their precise opportunity cost’. As a result he argues that whether an intervention represents an efficient use of resources ‘…can only be answered by establishing (implicitly or explicitly) our generic WTP for an additional unit of effect’ [6]. But by doing so, the comparison between health benefits produced and health benefits forgone under an opportunity cost approach is now replaced by some assessment of the subjective value of the additional health benefits of the new intervention, independent of any consideration of where the additional resources for the new program will be taken from or any assessment of the health benefits to be forgone. Hence this approach of using an arbitrary threshold is not consistent with the underlying objective of maximizing health outcomes from existing resources. Furthermore, the use of a fixed ICER threshold implies that all interventions satisfying this threshold are efficient (i.e., their implementation represents an efficient use of healthcare resources) no matter how many interventions this involves or the resource requirements to implement them. Hence it assumes that the marginal utility of health effects is constant and that there is a stream of additional resources, of an unknown size, available at a constant marginal opportunity cost [7,8]. In other words, Dowie’s prescription for dealing with the noneconomic basis of the ‘kinked’ ICER threshold itself lacks a valid economic foundation.

Illustrative example

The following example illustrates the limitations of the threshold ICER approach, showing that it uses a one-dimensional approach to address what is a two-dimensional problem. Information on the size of resource requirements (i.e., incremental costs) and health benefits (i.e., incremental effects) of healthcare interventions, if fully implemented, are not reflected in the ICER. Hence use of the ICER threshold does not determine whether the resources released from implementing an intervention in the SW quadrant will be sufficient to fund the new intervention in the NE quadrant, irrespective of the size of the ICER values of the two interventions. Choosing to implement a new intervention in the NE quadrant does not require finding another intervention to implement in the SW quadrant (i.e., releasing sufficient resources by substituting a less costly, less effective intervention for a more costly, more effective intervention). Under the threshold decision rule used by Dowie, if a program in the NE quadrant has an ICER value below the threshold value, λ, that is sufficient evidence to determine that the intervention represents an efficient use of resources.

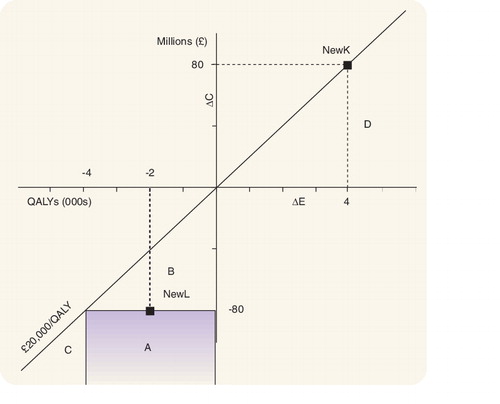
The failure of this approach to determine whether an intervention is efficient is illustrated in the CE plane in (Figure 1). The CE plane is divided into two areas, above and below the threshold ICER of £20,000/QALY. In the SW quadrant, the area under the threshold ICER describes interventions that are less costly but also less effective than the current interventions against which they are compared. Under the threshold ICER approach any intervention that falls below the ICER threshold is deemed cost-effective since the resources released per QALY lost are greater than the maximum acceptable costs per QALY gained in the NE quadrant as determined by the threshold ICER. In other words, according to Dowie, we could use these resources to fund interventions that fall below the ICER threshold in the NE quadrant (i.e., programs in area D in (Figure 1)) that generate a compensating amount of QALYs and still have some resources left over.

Consider a healthcare intervention NewK, which costs an additional £80,000,000 and generates an additional 4000 QALYs (Figure 1). Assume, for simplicity, that the decision maker is looking for one intervention in the SW quadrant whose adoption will release enough resources to fund NewK. All interventions below the line representing the threshold ratio in the SW quadrant of the cost–effectiveness plane release more resources per QALY lost than NewK costs per QALY gained. However, this does not determine whether the resources released by implementing an intervention in the ICER-acceptable part of the SW quadrant will release sufficient resources to fund the additional resource requirements of NewK in the NE quadrant. For example, any intervention in area B (Figure 1), does not release sufficient resources to fund NewK, although it is located in the ICER-acceptable part of the SW quadrant. Interventions in area C release sufficient resources to support the additional resource requirements of NewK but the health effects forgone by adopting these interventions are greater than those gained by introducing NewK. Hence areas B and C (which are in the ICER-acceptable part of the SW quadrant) are not consistent with the objective of improving efficiency in the allocation of resources and may therefore be described as unethical in terms of Dowie’s arguments. So which area on the cost–effectiveness plane is consistent with Dowie’s ethical arguments?

The solution

Any intervention in area A will release sufficient resources to support the additional resource requirements of NewK and will lead to an overall gain in health outcomes (i.e., it increases the efficiency in the allocation of resources). In (Figure 1), NewL represents such a program and will lead to a gain of 2000 QALYs if the released resources are used to fund NewK. Area A in (Figure 1) can be more elegantly presented as the SE quadrant of a decision making (DM) plane (Figure 2) introduced by Sendi and colleagues (2002) and graphically describes the alternative decision rule for determining whether an intervention represents an efficient use of resources [9]. Under this decision rule, opportunity cost considerations are considered explicitly and assumptions about perfect divisibility and constant returns to scale are not required. In order to introduce a new intervention K that costs more than the existing intervention for the same patients, another intervention (or interventions) L must be found that, if implemented, releases sufficient resources to fund the additional resources required for K but reduces health benefits by less than the additional health benefits of K [3,13]. This decision rule has been extended for situations where costs and effects are uncertain and a more formal definition has been reported elsewhere [9,14]. The difference in incremental costs (ΔC(K)- ΔC(L)) and effects (ΔE(K)- ΔE(L)) between NewK and NewL are indicated on the vertical and horizontal axis of the decision making plane, respectively (Figure 2). All evaluations that yield outcomes in the SE quadrant of the decision making (DM) plane are consistent with the alternative decision rule of CEA and do not rely on assumptions that may jeopardize the ethical arguments to justify the objective of efficiency.

Epilog

The arguments to justify why cost-effectiveness should trump effectiveness inherently stems from the realization that we are living in a world where healthcare resources are limited. However, a threshold ICER cannot be used to determine which interventions, if adopted, will lead to an increase in the efficiency of use of healthcare resources. Although Dowie notes the importance of opportunity costs in determining the efficiency of resource use, in the absence of information on opportunity costs he is prepared to settle for a generic measure of WTP for a QALY. In doing so he fails to recognise that this changes the nature of the question being addressed and introduces unrealistic assumptions, for example, about WTP for QALYs being independent of the number of QALYs being ‘purchased’. As shown elsewhere, the current use of ICER thresholds in healthcare decision making has resulted in uncontrolled growth in expenditures without any evidence of increase in overall health gains of the community [12,15]. Instead, the SE quadrant of the decision making plane identifies those interventions that underlie Dowie’s concerns that effectiveness not be a prerequisite for cost-effectiveness.