Hess Altitudes and Other Morphological Estimators of Glacier Equilibrium Lines

Abstract

The Hess altitude h on a valley glacier is the altitude of that contour that is most nearly straight. The Kurowsky altitude k is the average of the glacier’s minimum and maximum elevations. The glaciation level g of a glacierized region is the average of the elevations of the lowest glacierized and the highest unglacierized summits. We study the relationships between these morphological variables in well-mapped areas in Axel Heiberg Island, Nunavut, and in northern British Columbia, and also in a set of more widely distributed glaciers with well-known equilibrium-line altitudes e. We confirm that the relationships are strong, although their dispersion is considerable both for single glaciers and at the regional scale. On average h is 130 m below the long-term mean equilibrium line, k is slightly below it, and g is 200 m above it. There is very little morphoclimatic information in h that is not also conveyed by k, and since the latter is faster to measure and is already tabulated for tens of thousands of glaciers, its use is preferable. The glaciation level is less concordant. We suggest that it records interactions between landscape and climate on a somewhat slower time scale. The linear dependences of h on k and g, and of e on each of the 3 morphological estimators, have slopes slightly but significantly less than 1. This result is not yet understood.

Introduction

The Hess altitude, on any glacier of suitable morphology, is the altitude of that contour that is most nearly straight. Maps of most valley glaciers show that contours are concave in the accumulation zone and convex in the ablation zone. The curvature of the contours changes sign somewhere between the accumulation zone and the ablation zone, and it is natural to conjecture that the contour with the least curvature coincides nearly with the equilibrium line of the glacier. A cartographic measurement of the Hess altitude is thus likely to convey useful climatological information about the glacier. The measurement will often be easy, so the Hess altitude sounds like a promising probe of glacier climatology as averaged over the response time of the glacier.

There are, however, few published measurements of Hess altitudes since those made by Hess himself on maps of the Alps (Hess, 1904). Zverkova et al. (1982), Fountain et al. (1999; see also Leonard et al., 1998), and Leonard and Fountain (in press) are rare modern examples, and Miller et al. (1975) relied in part on the Hess method. Modern textbooks such as Sugden and John (1976), Bradley (1985), and Benn and Evans (1998) ignore the idea, which is explained in passing by Andrews (1975), who refers to Østrem (1966). Østrem describes Hess's method thus: “It is possible to determine the boundary between the accumulation area and the ablation area, as the contour lines will indicate a concave surface pattern in the former and a convex pattern in the latter. In between there is normally an area in which one or two contour lines are shown almost straight. This will be the long-term mean position of the firn line providing the glacier is flowing in an almost parallel-sided channel in the firn line region.” Although we adopt this definition, which is the same as that used by Zverkova et al. (1982), it does not define the quantity described by Hess (see Appendix).

Østrem's glaciation level (1966, 1972), to judge again by the textbooks, has become a standard measurement. The concept can be traced back to Brückner (1887). For a given region, it is the average of the summit elevations of the lowest glacier-bearing and the highest glacier-free mountain. Østrem anticipated, and was partly able to confirm, that the glaciation level would lie 100–200 m above the glacier equilibrium-line altitude. The glaciation level has been mapped for several glacierized regions, including our study regions in western Canada (Østrem, 1972) and arctic Canada (Miller et al., 1975).

Østrem also mentions what we call the Kurowsky altitude, which for any one glacier is the average of its lowest and highest points. Since Kurowsky proposed this quantity as a measure of the equilibrium-line altitude (Kurowsky, 1891) it appears to have been used little if at all, perhaps because other authors have followed Hess and Østrem in suspecting that it gives values which are too high.

The Hess altitude may be estimated for any glacier on which a meaningful change in the sign of contour curvature can be identified. Indeed, several such changes may be identifiable on tributary streams of a single glacier. Unlike the glaciation level, it is thus a local as opposed to a regional estimate. Among our motives for studying Hess altitudes, then, was to find out whether the additional labor of local-scale data collection, relative to that required for determining glaciation levels, is repaid by a proportionate increase in glaciological understanding.

Our aims here are to improve awareness of the Hess altitude and to document its relationship to other morphological estimators and to the equilibrium-line altitude itself. We present measurements of Hess altitudes made on maps of different scales in western and arctic Canada. We explore the uncertainties in the measurements by comparing the work of two map readers, and we compare Hess altitudes with Kurowsky altitudes, glaciation levels, and observed equilibrium-line altitudes. In an appendix we offer a translation of the defining passage from Hess's textbook.

Data Sources and Methods

We studied a 1:50,000-scale map of the Thompson Glacier region, Axel Heiberg Island, Nunavut (National Research Council, 1962; contour interval c = 25 m), and a transect of 1:50,000-scale National Topographic Series maps crossing the western Cordillera in northern British Columbia (c = 30 m). In the former area, maps were also available at scales of 1:10,000 (National Research Council, 1965; c = 10 m), 1:100,000 (McGill University, 1963; c = 100 m), and 1:250,000 (NTS sheet 59H, Department of Energy, Mines and Resources, 1967; c = 152 m), and these were used to evaluate the influence of map scale on the measurements. A detailed error analysis of the Axel Heiberg Island maps was presented recently by Cogley and Jung-Rothenhäusler (in press). The British Columbia transect included 20 maps showing glaciers in the zone between 56°45′N and 57°15′N, but on four of these no Hess and/or Kurowsky altitudes were identifiable, and on a further two there was only one collocated pair of altitudes.

To augment these resources we took 37 pairs of Hess and Kurowsky altitudes from Hess (1904), which we treated as a single map, and 7 pairs from Zverkova et al. (1982). The latter, from maps of the Caucasus at 1:25,000 scale with c = 10 m, were also treated as a single map for lack of information on sample sizes. We also assembled maps of glaciers with multiannual measurement series of equilibrium-line altitude e. For 15 such glaciers we had Canadian topographic maps, and for a further 22 we located other published maps. Most of these, showing single glaciers at scales between 1:5000 and 1:25,000 with contour intervals of 5 to 20 m, were annexed to volumes III–VII of Fluctuations of Glaciers (e.g., Haeberli et al., 1998). Most of the glaciers are in Scandinavia and the Alps, with Svalbard, Kirghizia, Tibet, and Kenya also represented. Averages and standard errors of e were taken from Dyurgerov (2002).

For each glacier or glacier tributary on which an estimate could be made we recorded the location and elevation h of the straightest contour (the Hess altitude), the aspect of the glacier in the neighborhood of that contour, and the minimum and maximum elevations z _min and z _max of the glacier. We computed the Kurowsky altitude as k = (z _min + z _max )/2. The precision of elevations was of course constrained by the contour interval. We sometimes took for h the average of 2 adjacent contours where the upper was concave and the lower convex. For each map showing at least one glacier, we estimated the glaciation level g as described by Østrem (1966).

At scales larger than about 1:25,000, maps of glaciers typically resolve features smaller than one ice thickness (about 100–200 m) in horizontal extent. Supraglacial moraines and the valleys of supraglacial meltwater streams are examples. These features can make it paradoxically harder to identify the Hess altitude than on small-scale maps, because the curvature of contours is influenced by small-scale processes not directly related to the glacier dynamics of which the Hess altitude is presumed to be a reflection. An additional complication arises from the cartographic practice of drawing straight contours through steep icefalls, where the glacier surface is extremely irregular. We addressed these complications by exercising subjective judgement. It would be possible to automate the identification of Hess altitudes, for in principle the problem of choosing a line of least curvature is not difficult, but a very substantial effort would be needed to develop an algorithm competitive with subjective judgment in the tasks of filtering or smoothing away nondynamical surface features and rejecting false candidate contours.

Uncertainties

REPRODUCIBILITY

Two map readers measured Hess altitudes on a 1:50,000-scale map (National Research Council, 1962). Table 1 shows that the two readers produced estimates of h and k that were unbiased; their averages did not differ significantly from 0. The rms differences between the two readers' estimates of h, 29 m, and k, 14 m, were of the order of 1 contour interval. The lesser rms difference for k is to be expected because it is more straightforward to measure k, but that it is not 0 shows that different decisions about minimum and maximum glacier elevations were made during map reading. The readers' estimates of the difference (h − k) were very similar: about −20 m on average over the map. Neither estimate is reliably distinguishable from 0. The rms differences for (h − k), approaching 100 m, measure the dispersion of this quantity in the sample available on the map and are comparable with the dispersions (standard deviations, not tabulated) of the individual readings of h and k, which lie between 70 and 96 m.

In this and following comparisons, the rms difference may be interpreted as proportional to the uncertainty in any single-glacier estimate of (h − k), while the standard errors attached to the mean difference measure the uncertainty in regionally averaged estimates. (Note, however, that the error range attached to the mean in the tables is twice the standard error.)

EFFECTS OF MAP SCALE

Although it was not our principal purpose, we studied the effect of map scale on estimates of h and k because most of the Canadian High Arctic is mapped only at 1:250,000, and it would be worthwhile to have an understanding of how this small scale might compromise measurements made over the wider area. Further, many of the 1:50,000-scale maps of northern British Columbia are available only as monochrome prints on which map reading is necessarily slower than on colored prints.

Differences between estimates of h and k made at different scales are summarized in Table 2. The picture that it conveys is not perfectly regular, which we consider to be due mainly to small sample sizes. The 1:10,000-scale map covers only a single glacier, while at 1:250,000 scale many measurement points recognizable at 1:50,000 and 1:100,000 are lost because of generalization. In addition the 1:100,000 scale map is in part redrawn from the 1:50,000-scale map. In spite of these shortcomings, we see a tendency for mean differences to grow as the scale of the smaller-scale map increases. Three of the smaller-scale comparisons show mean differences that appear to differ significantly from the expected value of 0. The rms differences also increase in the same direction. Loss of resolving power on smaller-scale maps would explain this observation consistently.

Table 3 compares differences (h − k) estimated on maps of different scale. All of the mean map-to-map differences are consistent with each other and with the mean differences of the previous subsection. The 1:10,000-scale estimate stands somewhat apart from the others, but this may be because the sample is small. The uncertainty at 1:250,000 is notably greater than at 1:50,000 and 1:100,000. Rms differences increase as map scale decreases. Thus, 1:250,000-scale maps yield more uncertain measurements, but there is no evidence that these results are biased. Their uncertainty can be reduced appreciably by averaging over an area comparable with that covered by a typical 1:50,000-scale topographic map.

COMBINED UNCERTAINTIES

Errors in estimates of h and k will consist of contributions from (1) mapping error, or the failure of the contours to represent the terrain accurately; (2) map-reading errors, or the failure of the reader to estimate and record elevations accurately; (3) the faulty exercise of subjective judgement as described earlier; and (4), for regional averages, a component of sampling uncertainty. Mapping errors are the same for all cartographic estimates of elevation made from any one map. This includes estimates of e, which are invariably based on existing cartography. Map-reading error is due to blunders and to incorrect interpolation between contours for estimates of z _min and z _max . Cogley and Jung-Rothenhäusler (in press), analyzing errors in the Thompson Glacier maps, found that map-reading error was small relative to mapping error. It is likely that the largest contribution to uncertainty in the present analysis comes from subjective judgment, which by definition is difficult to quantify. Accordingly, we fall back on the finding of Cogley and Jung-Rothenhäusler (in press) that total error in elevation (mapping error plus map-reading error) is well approximated, for purposes such as the present, as one-half of the contour interval c. To try to ensure that our error bars allow generously for subjective uncertainty, we will assume that the standard errors of single-glacier estimates of h and k are equal to c. This is consistent with the empirical between-reader comparisons described earlier.

One might argue that k is known more objectively than h, but we neglect this point because, first, k depends on two estimates of elevation, not one, and second, estimates of k for glacier tributaries have z _min in common and therefore are not independent.

We assume that sampling uncertainty in regional averages is represented adequately by conventional statistics. This, indeed, may be a persuasive argument for preferring <h> and <k> to glaciation level g as a regional-level quantity, for g is measurable at a density no greater than one estimate per map (or other region of adequate size). It is thus hard to generate error estimates for g. Where error estimates are needed below, we assume that se(g) is equal to the root sum of squares of its component standard errors (the two summit elevations), which in turn we assume to be equal to c. Thus, se(g) = .

Results

ASPECT

Graphs and statistics for the variation of Hess and Kurowsky altitudes with glacier aspect show no evidence within any single map, or in the entire pooled sample, for systematic variation of either h or k. Sampled glaciers are themselves distributed uniformly around the compass, and so are the measured h and k. We therefore do not consider aspect further as a variable that might control glacier morphology.

REGIONAL COMPARISONS

Table 4 summarizes our regional-level comparisons of h, k, and g. We include Hess's own comparison of h and k for glaciers in the Alps (Hess, 1904), and data from Zverkova et al. (1982). Table 5 shows that, contrary to preliminary indications from the Thompson Glacier analysis, regional Hess and Kurowsky altitudes do indeed differ significantly. On average h is some 200 m below k, and the difference is strongly significant. Variability from map to map is, however, large; the rms difference exceeds 200 m. The dispersion of <h − k> is less, the standard deviation in this sample (not tabulated) being 122 m. The glaciation level g is even further above the average Hess altitude <h>, by about 350 m. As with <h − k>, the variability of <h> − g, 400 m, is somewhat greater in magnitude than the mean difference. Its dispersion, 187 m, is less than the rms variability.

Figure 1 illustrates two of the pairwise relationships between morphological measures. They are rather strong: the square of the coefficient of correlation is 94% in Figure 1a and 64% in Figure 1b. There are at least two further points of interest. First, the relationship between <h> and <k> is stronger than that between <h> and g, suggesting that the glaciation level carries morphoclimatic information of a somewhat different sort than that carried by the Hess and Kurowsky altitudes. Second, both of the slopes, dh/dk and dh/dg, are probably less than the value of unity that might have been expected: dh/dk differs from 1.00 by more than 3 standard errors, and dh/dg by 1.3 standard errors.

Figure 2 illustrates the frequency distribution of h − k for all single glaciers and tributaries contributing to Figure 1. The distribution is approximately normal, although the presence of some extremely large differences suggests that we may have failed to identify and reject some outliers as blunders. The average single-glacier difference, −155 ± 23 m, is not very far from the average of the 19 map averages, −188 ± 65 m (<h − k>, Table 5), and the standard deviation of 182 m is a measure of the reliability of either morphometric measure as a predictor of the other for any one glacier.

COMPARISONS WITH THE EQUILIBRIUM-LINE ALTITUDE

Measurement series for glacier mass balance, and their associated estimates of e, were still relatively short at the time when Østrem (1972) and Miller et al. (1975) mapped the glaciation level over northern British Columbia and the Canadian High Arctic, respectively. Even today there are few such series, but naturally they are longer, and there is now a sufficient number available for well-mapped glaciers that it seems worthwhile to compare these measurements with their alleged cartographic estimators.

Table 6 summarizes the comparison for 15 Canadian and 22 other glaciers for which we were able to measure h and k. Measurements of g were possible only on the Canadian topographic maps. The Hess altitude is on average 130 m below the long-term mean equilibrium line, the Kurowsky altitude is slightly below it, and the glaciation level is 200 m above it. These mean differences are consistent with those found in Table 5. Rms differences between e and the three morphological measures are of the order of 100–200 m, and the observed ranges of differences are 400–750 m. Figure 3 illustrates the relationships between e and the morphological measures. As in Figure 1, the relationships are linear and strong, although again that involving g is somewhat weaker. We have more confidence in these relationships because, although sample sizes are still only moderate, all of the data are from single glaciers and there is no regional variability to be accounted for. Again we find that the slopes differ significantly from unity (see Table 6 for details). This surprise apart, however, Figure 3 first confirms the impression created by Figure 1 that all three of the morphological measures are robustly and reliably, if not very precisely, related to each other, and second shows that they are also robust and reliable, if imprecise, as estimators of the mean equilibrium-line altitude.

Discussion

Once familiar with the work, a trained map reader needs not less than 1 h to record the Hess and Kurowsky altitudes of a moderately glacierized map sheet, to be compared with about 10 min for the glaciation level. Hess measurements consume about twice as much time as Kurowsky measurements because, although the Hess contour is immediately recognizable on ideal glaciers, doubtful cases demand thoughtful study. The ratio of insight to effort is greatest for k, for at the regional (map) level one obtains both <k> and a measure of uncertainty by investing somewhat more time than required to obtain g, which is not accompanied by a standard error. The Hess altitude, calling for up to twice the effort, contains very little morphoclimatic information that is not also contained in the Kurowsky altitude. These considerations favor k strongly, as does the fact that its components, z _min and z _max , are already tabulated for tens of thousands of glaciers in the World Glacier Inventory (available from www-nsidc.colorado.edu/data/glacier_inventory/index.html).

This does not mean that Hess measurements are necessarily unprofitable. That Hess altitudes should be consistently recognizable and consistently about 130 m below the equilibrium line, and that the equilibrium-line altitude should be consistently about halfway between the top and bottom of the glacier, are facts not explained by our current understanding of the interaction between landscape, ice dynamics, and climate in mountainous regions. A more thorough study of the Hess altitude would be likely to improve our ability to model the dynamics of valley glaciers.

The Kurowsky altitude turns out to be very near the equilibrium-line altitude, nullifying the suspicions voiced by Hess (1904), Østrem (1966), and others. Our result agrees, however, with that reported briefly by Leonard et al. (1998).

The finding that the glaciation level is 200 m above the equilibrium line agrees with the explanation suggested by Østrem (1966), which is simply that g is determined from summit elevations rather than from somewhat lower elevations on the glacier itself. Miller et al. (1975) drew attention to a northward increase in e − g in eastern Canada, from −450 m in Labrador to ∼0 m in northernmost Ellesmere Island, but the pertinence of this observation may be affected by differences in measurement cell size, a few hundred km² in our work and Østrem's against 2500 km². Humlum (1986) showed that larger cells lead to smoother glaciation-level surfaces with less pronounced local peaks. Nevertheless, Miller et al.'s observation may be relevant to the explanation of the relationships seen in Figures 1 and 3.

It is unexpected and surprising that these linear relationships should all have slopes less than 1. In Figure 1 the results are in part debatable, for the slope dh/dg is only marginally distinguishable from unity. The results in Figure 3 are more difficult to dismiss. We speculate that if they were to survive a more extensive investigation the explanation would be found to be dynamical and related to glacier temperature. That is, higher glaciers (upper right of each figure) would be found to be colder and therefore stiffer, and we could account for the observed difference in morphology in terms of glacier flow. (Equally, they might be warmer and less stiff. We do not have estimates of temperature, nor do we know how the viscosity of ice would affect the morphological measurements.) Clearly, however, if the effect is real it is subtle, and it is not possible to say more with the information now available.

Table 5 shows g to be a slightly weaker estimator of <h> than is <k>, and Table 6 shows that both h and k are better than g as estimators of e. This is not to disparage g, which is the most readily measured of the morphological variables. We prefer to interpret the finding as showing that g contains somewhat different information than that carried by h and k, and we suggest that this is because g represents interactions between landscape and climate over a somewhat slower time scale. Changes in climate are reflected immediately in e, while the Hess and Kurowsky altitudes will adjust over the response time of the glacier (Jóhannesson et al., 1989). For g to change, however, it is necessary for at least one glacier to appear or disappear in the measurement region. In a time of prevalent glacier mass loss, such as the present day, we must wait for one glacier in a suitable location to cease to exist before we observe a change in glaciation level, and perhaps for the disappearance of many glaciers (or of none, for a sufficiently small climatic change) before g is once more in equilibrium with the climate as measured by e. While we are waiting, both h and k will be adjusting gradually.

The morphological variables are of value primarily for regional and broader-scale analyses. The dispersions and rms differences discussed above are of the order of 1 to a few hectometers, meaning that the morphological estimators of equilibrium-line altitude are of limited use on single glaciers. To provide a perspective on this point, we normalized the differences e − h and e − k of Table 6 by dividing them by the elevation ranges, Z = z _max − z _min , of the glaciers. On average (e − h)/Z is 20%, with a standard deviation of 17% and a range from −23% to +55%. (e − k)/Z averages 6%, with a standard deviation of 16% and a range from −50% to +41%.

A variety of measures is used to reconstruct former glaciers, particularly those of the Wisconsinan (Benn and Lehmkuhl, 2000). It is of interest to note that the Hess altitude offers a modern analogy for the maximum-elevation-of-lateral-moraines method reviewed by Benn and Lehmkuhl. Contemporary evidence confirms the expectation that lateral moraines will extend upglacier almost but not quite to the equilibrium line, and their maximum elevation should therefore be close to the Hess altitude. The analogy between the Kurowsky altitude and the reconstruction methods known as “toe-to-headwall-altitude ratio” methods is already plain, the Kurowsky altitude corresponding to a ratio of 0.5. Thus, both contemporary cartographic measures have paleoclimatic counterparts. The Hess altitude, not requiring fieldwork, might prove useful in calibrating the lateral-moraine method and estimating its uncertainty. This would contribute, for example, to resolving the persistent problem of tropical snowline changes since the last glacial maximum (Porter, 2000).

Conclusion

The findings of this work are negative in the sense that we began with the aim of learning more about the Hess altitude, and we are ending by recommending the use of a different morphological measure, the Kurowsky altitude. But the Hess altitude is clearly a recognizable feature of valley-glacier morphology, and its correlations with the Kurowsky altitude, the glaciation level, and the equilibrium-line altitude can all be considered well established. There is more to be learned about these connections, which at present are understood only empirically. The results presented here, particularly the quantified estimates of uncertainty, will be useful both in probing for dynamical explanations of the observations and in the traditional role played by cartographic morphological estimators: displaying and seeking to account for regional and broader variations in glacierization. Short of returning to the aerial photographs from which they were drawn, maps drawn during the 20th century are the only extensive source of reference states from which to gauge changes in glacierization up to the present and into the future. At the least, measures such as the Kurowsky altitude will be valuable as illustrative tools in ambitious ventures such as GLIMS (Global Land Ice Measurements from Space) (Kieffer et al., 2000), and their value may go beyond illustration to enhanced understanding, particularly when it becomes possible to map their changes over time.

FIGURE 1. (a) Relationship between mean Hess altitude <h> and mean Kurowsky altitude <k> for 17 maps at 1:50,000 scale (circles) and for the measurements of Hess (1904; square) and Zverkova et al. (1982; triangle). Maps with only one h − k pair are represented by open symbols. The thin diagonal line represents equality of <h> and <k>. The parameters of the thick line fitted to the data are obtained with an algorithm of Press et al. (1992; section 15.3), which takes account of uncertainty in both dependent and independent variables; see Table 5 for further statistical details. (b) Relationship between mean Hess altitude <h> and glaciation level g for 17 maps at 1:50,000 scale. Details as for panel a

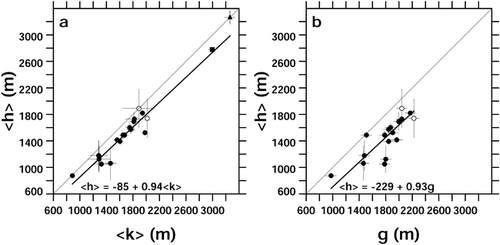
FIGURE 2. Frequency distribution of the difference of single-glacier h − k in the pooled sample from all maps. Vertical dashed line: mean difference, −155 m. The standard deviation of the sample is 182 m

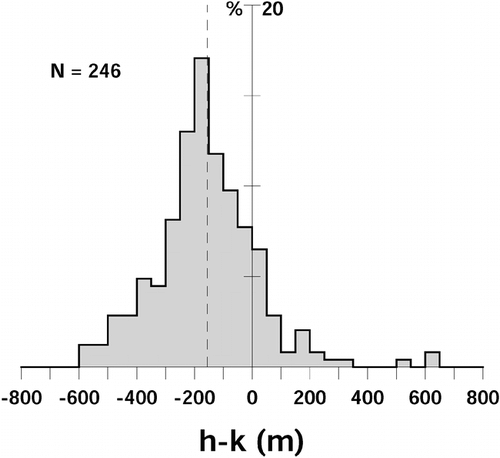
FIGURE 3. (a) Relationship between equilibrium-line altitude e and Hess altitude h for 37 glaciers. (b) Relationship between e and Kurowsky altitude k. (c) Relationship between e and glaciation level g for 15 glaciers. Regression parameters were obtained as in Figure 1

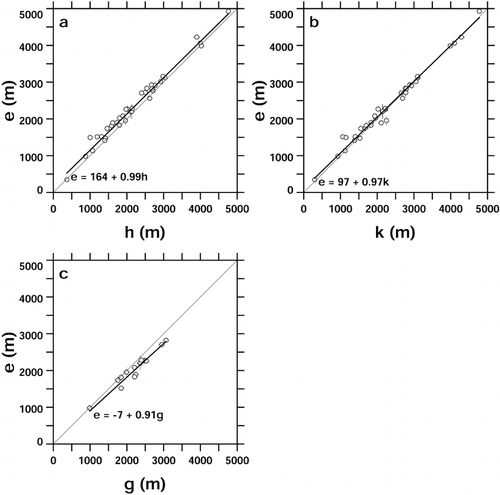
FIGURE A1. Figure 11 of Hess (1904), showing contour patterns in the ablation (a) and accumulation (b) areas of a typical valley glacier. Contours are solid on land and dotted on glacier ice. Hess's aim was to contrast the sharp inflections at the glacier margin in the ablation zone with the smooth transition from land to ice in the accumulation zone, but later authors have focused on the contrast in curvature on the glacier, convex in the ablation zone and concave in the accumulation zone

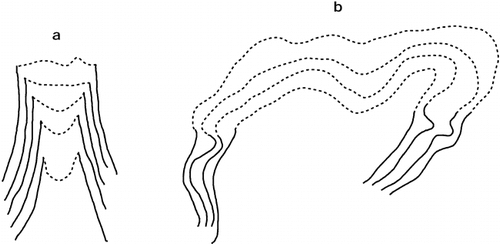
Table 1 Between-reader differences^a (Thompson Glacier region)

Table 2 Between-map differences^a (Thompson Glacier region)

Table 3 Between-map differences of differences^a (Thompson Glacier region)

Table 4 Regional variations of glacier morphology

Table 5 Summary of regional glacier morphology

Table 6 Comparison of morphological measures with measured equilibrium-line altitudes

Appendix:

Hess's Description of the Hess Altitude

Hess (1904) describes three cartographic estimates of the firn line altitude: that of Partsch (1882), which relied on the lowest elevation at which perennial snowpatches are found; that of Brückner (1887), which is the elevation that gives an accumulation area ratio of 3/4; and that of Kurowsky (1891), which, assuming that accumulation and ablation are linear functions of elevation, is simply the average elevation of the glacier. He then continues (translated from pp. 69–70 of his German text):

IV. I have given some attention to a fourth method. It relies, like Kurowsky's method, on good cartography in which the form of the land is represented by contours, and especially on the observation that the form of the contours in the ablation zone is essentially different from that of the firn zone contours. Here the contours pass without a sharp change of direction from the firn into the surrounding bedrock areas (Fig. 11b [see Figure A1b]); in the ablation zone, however, because ablation at the glacier margins is greater than in the middle, the contours must take the form shown in Fig. 11a . . . [see Figure A1a]; they must pass from (debris-free) ice onto the rock with a sharp change of direction. Thus, if one seeks on the map that part of the glacier margin where there is a transition from the one kind of isohypse to the other, this gives one a point on the firn line. Such points will not always lie in the horizontal; the points found on the two margins of a glacier will often be at different heights on account of variably favorable orography. It is to be noted, moreover, that morainal cover only appears in the ablation zone, so that for a large number of valley glaciers the course of the firn line can be determined fairly readily, and its average vertical position easily estimated, by this method.

The method has at any rate the advantage of simplicity. The results to which it leads agree with reality quite well in my experience. It must not be denied, however, that the passage from one contour form to the other cannot always be identified unambiguously.