Current recommendations on the estimation of transition probabilities in Markov cohort models for use in health care decision-making: a targeted literature review

Abstract

Objective

Although Markov cohort models represent one of the most common forms of decision-analytic models used in health care decision-making, correct implementation of such models requires reliable estimation of transition probabilities. This study sought to identify consensus statements or guidelines that detail how such transition probability matrices should be estimated.

Methods

A literature review was performed to identify relevant publications in the following databases: Medline, Embase, the Cochrane Library, and PubMed. Electronic searches were supplemented by manual-searches of health technology assessment (HTA) websites in Australia, Belgium, Canada, France, Germany, Ireland, Norway, Portugal, Sweden, and the UK. One reviewer assessed studies for eligibility.

Results

Of the 1,931 citations identified in the electronic searches, no studies met the inclusion criteria for full-text review, and no guidelines on transition probabilities in Markov models were identified. Manual-searching of the websites of HTA agencies identified ten guidelines on economic evaluations (Australia, Belgium, Canada, France, Germany, Ireland, Norway, Portugal, Sweden, and UK). All identified guidelines provided general guidance on how to develop economic models, but none provided guidance on the calculation of transition probabilities. One relevant publication was identified following review of the reference lists of HTA agency guidelines: the International Society for Pharmacoeconomics and Outcomes Research taskforce guidance. This provided limited guidance on the use of rates and probabilities.

Conclusions

There is limited formal guidance available on the estimation of transition probabilities for use in decision-analytic models. Given the increasing importance of cost-effectiveness analysis in the decision-making processes of HTA bodies and other medical decision-makers, there is a need for additional guidance to inform a more consistent approach to decision-analytic modeling. Further research should be done to develop more detailed guidelines on the estimation of transition probabilities.

Keywords:

• cost-effectiveness
• decision models
• probability
• transitions

Introduction

Health technology assessment (HTA) and medical decision-making, more generally, rely on the use of decision-analytic models. Such models synthesize clinical, epidemiological, quality of life, resource use, and cost data in order to generate estimates of health effects and associated costs. Markov models are a popular form of decision-analytic models which characterize patient cohorts based on a finite number of mutually exclusive and exhaustive “health states”. Under the Markov property, membership of future health states depends only on the current health state, and not on the events that occurred before.¹ Movement between health states is defined by “transition probabilities”, which determine the likelihood of a patient moving from one health state to another over a discrete period of time (the “cycle length”).¹

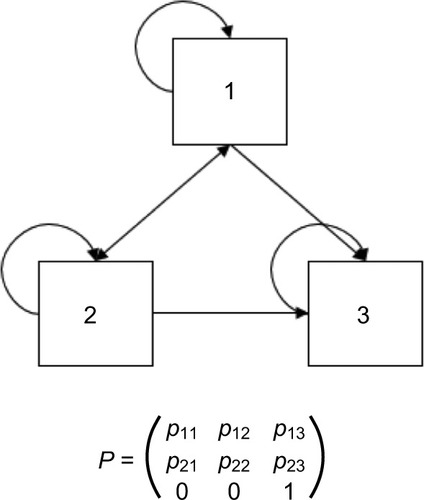
An illustrative example of a three-state Markov model with health states 1, 2, and 3 is presented in Figure 1; an example of health states for a model of a general condition may be asymptomatic disease, symptomatic disease, and death. Movements between health states are governed by a matrix P of transition probabilities p_rs, which describes the risk of moving from state r to state s ≠ r at time r over a model cycle of length u, and p_rr, which describes the probability of remaining in state r at time r over a model cycle of length u. One health state (in this case health state 3, and usually the health state corresponding to death) will act as the “absorbing state”, for which the probability of moving to any other state is 0 and the probability of remaining in the state is 1.

Figure 1 Illustrative example of a three-state Markov model.

Measures for cost and outcome can be associated with states and transitions to account for resource use during different stages of disease and the associated changes in health outcomes. These estimates of costs and outcomes may be accumulated over the course of the model and the cost-effectiveness of health technologies estimated.

The correct implementation of Markov models requires reliable and robust estimation of transition probability matrices (TPMs). In the simplest case, transition probabilities can be estimated in a straightforward manner using nonparametric methods based on observed counts for movements between health states in a data source. Briggs et al² describe the methods for calculating probabilities in this scenario.

However, calculating TPMs is challenging when the inputs to the economic evaluation cannot be derived directly and completely from a single dataset; for example:

• How should TPMs be constructed when not all transitions are observed within a dataset?

  Briggs et al² note that feasible transitions might not always be observed in all datasets, implying 0% probability of these transitions occurring. The authors advise not to exclude potential transitions because they were not observed in the data. Alternatively, a prior distribution may be specified; commonly, 1 is added to each cell count.

• How should subgroup analyses be performed in Markov cohort models?

  Subgroup analysis in Markov cohort models for economic evaluation is usually performed based on stratification of data, and estimation of transition probabilities at different values of t typically requires multiple partitions of the available data. This is often not an efficient use of data, and introduces many model parameters. An alternative approach is to allow covariate adjustment of the TPM. A growing body of literature has described these multi-state parametric models, which can be implemented in standard statistical software such as R, but have not yet been applied widely within economic evaluations for HTA submissions.^3–5

• How should treatment effects from clinical studies and meta-analyses be applied?

  It is common to apply relative effects to TPMs to estimate the probability of events for an intervention. Such treatment effects may be drawn from clinical trials directly or from formal evidence synthesis. Relative risks and odds ratios (unlike hazard ratios) are specific to the time period for which the event probabilities are defined. If the length of the trial or study reporting the relative risk (or odds ratio) is not the same as cycle length u, then applying this relative risk (or odds ratio) directly will be incorrect.⁶ Price et al⁶ present an adjustment to account for differences between the measured time point and the relative risk.

• How can we convert between alternative cycle lengths?

  It is well known that in order to convert a probability from one cycle length to another (e.g., from annual to 6-months), it must be done by first converting to a rate.^7,8 This is commonly achieved using the standard actuarial formula.⁹ However, conversion of a TPM from one cycle length to another is nontrivial; applying the actuarial formula to convert TPMs in models with more than two states introduces bias, because this ignores competing risk among states.¹⁰ More appropriate conversion requires taking the root of the matrix,¹⁰ or alternatively, choosing a short cycle length such that the probability of multiple clinical events occurring during a cycle is very small, thereby minimizing the bias.¹¹

• How should model calibration be performed if direct estimation of inputs is not possible?

  The objective of calibration is to “reverse engineer” the model of interest; essentially, to find input parameters so that the model predicts a known outcome (or outcomes). The analyst must make several decisions: there are multiple ways to define the objective function for the calibrated model, including approaches based on acceptable windows, minimizing deviation (absolute or in percentage terms), or the specification of likelihood functions. The selection of input parameters may also be performed using a number of methods. If multiple outcomes are to be calibrated against, and their input parameters are not independent, this can then become a complex optimization problem.¹² Welton and Ades¹³ provide an illustrated example of how to calibrate transition probabilities to be consistent with information from a particular study.

• How should missing data be handled?

  A commonly recommended strategy for addressing missing data within economic evaluations is multiple imputation.¹⁴ Under multiple imputation, each missing value is replaced with multiple predicted values; a vector of M≥2 possible values is created.¹⁵ M complete datasets are created, each with different imputations for the missing data. The data-sets can then be analyzed together using standard statistical methods and uncertainty appropriately characterized using Rubin’s rules.¹⁵ In order to estimate transition probabilities nonparametrically following imputation, the analyst may, for example, assume that the observed value is represented by the mean of the values across the M datasets. However, this approach fails to recognize the uncertainty associated with the imputation process itself and as a consequence will underestimate uncertainty in the analysis. An obvious approach may be to estimate separate TPMs for each of the M datasets, and then sample between these alternative datasets in probabilistic sensitivity analysis. However, we are not aware of any studies assessing this.

Transparent and consistent decision-making relies on the availability of an accepted methodological approach to the calculation of TPMs; while individual researchers have contributed substantially to the discussion on these topics, the authors of the present study are not aware of any formal consensus statements or guidelines addressing questions such as those mentioned earlier. This targeted literature review therefore, sought to identify consensus statements or guidelines detailing how TPMs should be estimated for use in Markov models in the context of the economic evaluation of medical interventions.

Methods

A targeted literature review was performed to answer the following research question:

• What consensus statements or guidelines are available to inform the calculation of transition probabilities for use in Markov models for the economic evaluation of medical interventions?

  Consensus statements were defined as “documents containing suggestions or recommendations based on the collective opinion of an expert panel” and guidelines as “systematically developed statements to assist researchers, HTA bodies, and other professionals in decisions about appropriate methodological approaches”.

Search methods

A base strategy was developed and refined to specifically target publications relevant to the research question.

Electronic database search

Search strategies specific to each database were designed to focus on retrieval of the published articles most likely to be relevant to the research question. The search strategies were designed and run by an experienced medical librarian.

The following electronic databases were searched:

• Medline (OvidSP)

• Medline In-Process Citations & Daily Update (OvidSP)

• Embase (OvidSP)

• PubMed

• The Cochrane Library, which includes six databases (Cochrane Database of Systematic Reviews, Cochrane Central Register of Controlled Trials, Cochrane Methodology Register, Database of Abstracts of Reviews of Effects, Health Technology Assessment Database, NHS Economic Evaluation Database)

Electronic searches were limited to English language publications. No country or time limits were applied. Details on the search strategy can be found in Figure S1.

HTA website search

The electronic search was supplemented by a literature search for relevant guidelines on HTA agency websites. The HTA agencies whose websites were searched are listed in Table 1. Reference lists of identified HTA guidelines were screened to identify additional relevant publications. No language limit was applied to searches of HTA websites.

Table 1 HTA agency websites considered

Country	HTA agency
Australia	Pharmaceutical Benefits Advisory Committee (PBAC)
Belgium	Belgian Health Care Knowledge Centre (KCE)
Canada	Canadian Agency for Drugs and Technologies in Health (CADTH)
France	The French National Authority for Health (HAS)
Germany	Institute for Quality and Efficiency in Health Care (IQWiG)
Ireland	National Centre for Pharmacoeconomics (NCPE)
Norway	The Norwegian Medicines Agency (NoMA)
Portugal	National Authority of Medicines and Health Products (INFARMED)
Sweden	Dental and Pharmaceutical Benefits Agency (TLV)
UK*	National Institute for Health and Care Excellence (NICE), Scottish Medicines Consortium (SMC), All Wales Medicines Strategy Group (AWMSG)

Note:

* Including NICE Decision Support Unit reports.

Abbreviation: HTA, health technology assessment.

Study selection

Identified publications were screened by one reviewer, with any publication considered to be informative to the research question being included. Study selection occurred in three phases:

• Potentially relevant publications were identified based on their title; any title clearly irrelevant was discarded at this stage.

• Abstracts or keywords were used to screen the remaining articles in order to identify relevant publications for full-text review.

• The full text of each potentially relevant publication was reviewed.

Studies were included if they were guidelines or consensus statements on the calculation of transition probabilities from either clinical endpoints of clinical trials or from clinical parameters of indirect/multiple treatment comparisons in Markov models. Publications that were not produced on behalf of professional organizations, expert panels, or HTA bodies were excluded.

Results

Electronic database search

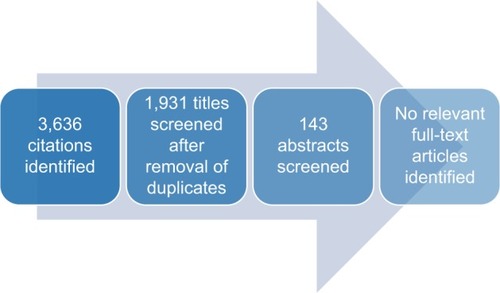
The electronic database search identified 3,636 publications; 1,931 unique publications were identified following deduplication (Table 2).

Table 2 Results of the electronic database search

Electronic database	Records identified	After deduplication
Medline	1,057	1,043
Embase	1,422	775
PubMed	1,098	111
The Cochrane Library	59	2
Total	3,636	1,931

Of the 1,931 unique publications identified, 1,788 publications were excluded on the basis of title review and 143 publications were excluded on the basis of abstract review. No guidelines on the estimation of transition probabilities for use in Markov models were identified via the electronic database search (Figure 2). However, 56 studies were considered to be of broad relevance, typically reflecting the viewpoints of individual authors or independent research groups as opposed to formal guidelines or recommendations. A list of the 56 publications considered to be of broad relevance can be found in Table S1.

Figure 2 Flow diagram of the screening process for the electronic database search.

HTA website search

The HTA website search identified 10 guidelines on economic evaluation. However, no identified guidelines included guidance or recommendations on the calculation of TPMs. One relevant publication was identified following review of the reference lists of guidelines selected through the HTA website search.⁸ The International Society for Pharmacoeconomics and Outcomes Research - Society for Medical Decision Making (ISPOR-SMDM) Modeling Good Research Practices Task Force recommend that the conversion of transition probabilities from one cycle length to another should be done through rates. However, no further details are provided.

Discussion

The aim of the targeted review was to identify formal recommendations, such as consensus statements or guidelines, to inform the calculation of transition probabilities for use in Markov models for the economic evaluation of medical interventions. One relevant publication was identified, in which the ISPOR-SMDM Modeling Good Research Practices Task Force recommended that the conversion of transition probabilities from one cycle length to another should be done through rates. However, many key questions around the estimation of TPMs for health care decision-making remain unanswered.

We searched a wide variety of data sources including electronic databases and HTA agency websites to identify relevant studies. However, our approach cannot be considered systematic. Our targeted review might not have captured all studies of interest given that relevant literature in this field is not always formally published as journal articles. Also, our searches of HTA agency websites were limited to ten; so it might be that relevant consensus statements or guidelines are available on unsearched HTA agency websites. Finally, our electronic database searches were limited to English language only, thus potentially leading to language bias and exclusion of relevant articles published in other languages.

This review was limited to modeling methods for medical interventions, and only included formal recommendations such as consensus statements or guidelines; we are aware that a substantial body of literature exists on the topic of estimating TPMs in the financial, engineering, and statistical fields, and from independent authors in the health eco nomics community which would not have been identified by our search protocol.

Therefore, it is recommended that additional research be conducted to consolidate and build on existing knowledge on this topic. An expert panel or working group should be convened to identify key circumstances in which the estimation of transition probabilities is not straightforward, or where the most appropriate approach is considered contentious. A broad systematic review of methodological publications on the topic of TPMs spanning all academic fields should be undertaken, and formal recommendations developed on the basis of the review, and as part of an iterative process amongst the expert panel or working group.

In the absence of consensus statements or guidelines, currently developed Markov models may utilize approaches that reduce accuracy, introduce additional uncertainty, or underestimate the uncertainty that exists. The development of formal guidance on the estimation of TPMs for health care decision-making would allow a more consistent approach to decision-analytic modeling, and therefore to decision-making.

Acknowledgments

We would like to thank Richard Grieve for the critical review of this manuscript and Dave Fox for developing the search strategy. This study was sponsored by Takeda Pharmaceuticals International AG. The abstract of this article was presented as a poster at the International Society for Pharmacoeconomics and Outcomes Research 19th Annual European Congress in 2016. The poster’s abstract has also been published.¹⁶

Supplementary materials

Figure S1 Search strategy.

Table S1 Potentially relevant publications identified via the electronic searches

Reference	Title
Aalen et al^Citation1	Covariate adjustment of event histories estimated from Markov chains: the additive approach
Alam et al^Citation2	Investigating the impact of structural changes in a nice single technology appraisal cost-effectiveness model
Alarid-Escudero et al^Citation3	Calibration of piecewise Markov models using a change-point analysis through an iterative convex optimization algorithm
Albert and Waclawiw^Citation4	A two-state Markov chain for heterogeneous transitional data: a quasi-likelihood approach
Allignol et al^Citation5	A competing risks approach for nonparametric estimation of transition probabilities in a non-Markov illness-death model
Andersen and Pohar Perme^Citation6	Inference for outcome probabilities in multi-state models
Black et al^Citation7	Determining transition probabilities from mortality rates and autopsy findings
Borgan^Citation8	Estimation of covariate-dependent Markov transition probabilities from nested case-control data. (Erratum is reference 9)
Borgan^Citation9	Erratum: Estimation of covariate-dependent Markov transition probabilities from nested case-control data (Original paper is reference 8)
Boruvka and Cook^Citation10	Sieve estimation in a Markov illness-death process under dual censoring
Cohen^Citation11	On estimating the equilibrium and transition probabilities of a finite-state Markov chain from the same data
Cooper et al^Citation12	Comprehensive decision analytical modelling in economic evaluation: a Bayesian approach
Craig and Sendi^Citation13	Estimation of the transition matrix of a discrete-time Markov chain
Dabrowska and Ho^Citation14	Confidence bands for comparison of transition probabilities in a Markov chain model
Debosscher^Citation15	Unifying stochastic Markov process and its transition probability density function
Denton and Spencer^Citation16	Modeling the age dynamics of chronic health conditions: life-table-consistent transition probabilities and their application
Diaby et al^Citation17	Survival modeling for the estimation of transition probabilities in model-based economic evaluations in the absence of individual patient data: a tutorial
Gaveau and Schulman^Citation18	Multiple phases in stochastic dynamics: geometry and probabilities
Gupta et al^Citation19	Transition probability estimation using repeated sampling from a fitted mixed model
Gupta et al^Citation20	Generalized implementation of Em algorithm for estimation of transition probability matrix
Hawkins and Han^Citation21	Estimating transition probabilities from aggregate samples plus partial transition data
Healy and Engler^Citation22	Modeling disease-state transition heterogeneity through Bayesian variable selection
Huang^Citation23	Integrated analysis of incidence, progression, regression and disappearance probabilities
Iacobelli and Carstensen^Citation24	Multiple time scales in multi-state models
Kassteele et al^Citation25	Estimating net transition probabilities from cross-sectional data with application to risk factors in chronic disease modeling
Kaushik et al^Citation26	A methodology to monitor the changing trends in health status of an elderly person by developing a Markov model
Li and Pack^Citation27	An application of Markov models in estimating transition probabilities for postmenopausal women with osteoporosis
Limwattananon and Limwattananon^Citation28	Constructing a state-transition model for an economic evaluation of cancer treatments
McCombs^Citation29	Pharmacoeconomics: what is it and where is it going?
Meidani and Ghanem^Citation30	Uncertainty quantification for Markov chain models
Meira-Machado et al^Citation31	Nonparametric estimation of transition probabilities in a non-Markov illness-death model
Meira-Machado et al^Citation32	Multi-state models for the analysis of time-to-event data
Miller and Homan^Citation33	Determining transition probabilities: confusion and suggestions
Milne^Citation34	Pharmacoeconomic models in disease management. A guide for the novice or the perplexed
Moussa et al^Citation35	Measuring the change in contingency tables using Markov models application to the effect of preceding conception on the next one
Muenz and Rubinstein^Citation36	Markov models for covariate dependence of binary sequences
Nagylaki^Citation37	The distribution of sojourn times in finite absorbing Markov chains
Neine et al^Citation38	Bayesian calibration method to estimate transition probabilities for a Markov model based on a continuous outcome measure: application in Parkinson’s disease
Ng and Cook^Citation39	Modeling two-state disease processes with random effects
O’Mahony et al^Citation40	Dealing with time in health economic evaluation: methodological issues and recommendations for practice
Oppe et al^Citation41	Comparing methods of data synthesis: re-estimating parameters of an existing probabilistic cost-effectiveness model
Paes and Lima^Citation42	A SAS macro for estimating transition probabilities in semiparametric models for recurrent events
Putter et al^Citation43	Tutorial in biostatistics: competing risk and multi-state models
Regnier and Shechter^Citation44	State-space size considerations for disease-progression models
Rodriguez-Girondo and Una-Alvarez^Citation45	A nonparametric test for Markovianity in the illness-death model
Rodriguez-Girondo and Una-Alvarez^Citation46	Testing Markovianity in the three-state progressive model via future-past association
Rodriguez-Girondo and Una-Alvarez^Citation47	Methods for testing the Markov condition in the illness-death model: a comparative study
Rosychuk et al^Citation48	Comparison of variance estimation approaches in a two-state Markov model for longitudinal data with misclassification
Rosychuk and Thompson^Citation49	Bias correction of two-state latent Markov process parameter estimates under misclassification
Saint-Pierre et al^Citation50	The analysis of asthma control under a Markov assumption with use of covariates
Spitoni et al^Citation51	Estimation and asymptotic theory for transition probabilities in Markov renewal multi-state models
Tattar and Vaman^Citation52	Testing transition probability matrix of a multi-state model with censored data
Tattar and Vaman^Citation53	The k-sample problem in a multi-state model and testing transition probability matrices
Titman^Citation54	Transition probability estimates for non-Markov multi-state models
Tsang et al^Citation55	Estimating Markov chain transition matrices in limited data samples: a Monte Carlo experiment
Welton and Ades^Citation56	Estimation of Markov chain transition probabilities and rates from fully and partially observed data: uncertainty propagation, evidence synthesis, and model calibration

References

• AalenOOBorganOFekjaerHCovariate adjustment of event histories estimated from Markov chains: the additive approach.[Erratum appears in Biometrics. 2003 Jun;59(2):452–453]Biometrics2001574993100111764270
   PubMed Web of Science ®Google Scholar
• AlamMFBartonPMonahanMInvestigating the impact of structural changes in a NICE single technology appraisal cost-effectiveness modelValue Health2015187A696
   Web of Science ®Google Scholar
• Alarid-EscuderoFEnnsEPeralta-TorresYEMaclehoseRKuntzKMCalibration of piecewise Markov models using a change-point analysis through an iterative convex optimization algorithmValue Health2015187A814
   Web of Science ®Google Scholar
• AlbertPSWaclawiwMAA two-state Markov chain for heterogeneous transitional data: a quasi-likelihood approachStat Med19981713148114939695193
   PubMed Web of Science ®Google Scholar
• AllignolABeyersmannJGerdsTLatoucheAA competing risks approach for nonparametric estimation of transition probabilities in a non-Markov illness-death modelLifetime Data Anal201420449551323807694
   PubMed Web of Science ®Google Scholar
• AndersenPKPohar PermeMInference for outcome probabilities in multi-state modelsLifetime Data Anal200814440543118791824
   PubMed Web of Science ®Google Scholar
• BlackWCNeaseRFJrWelchHGDetermining transition probabilities from mortality rates and autopsy findingsMed Decis Making199717187938994155
   PubMed Web of Science ®Google Scholar
• BorganOEstimation of covariate-dependent Markov transition probabilities from nested case-control dataStat Methods Med Res200211218320212040696
   PubMed Web of Science ®Google Scholar
• BorganOErratum: Estimation of covariate-dependent Markov transition probabilities from nested case-control dataStat Methods Med Res2003122124
   Web of Science ®Google Scholar
• BoruvkaACookRJSieve estimation in a Markov illness-death process under dual censoringBiostatistics201617235036326598559
   PubMed Web of Science ®Google Scholar
• CohenJEOn estimating the equilibrium and transition probabilities of a finite-state Markov chain from the same dataBiometrics19682411851875642403
   PubMed Web of Science ®Google Scholar
• CooperNJSuttonAJAbramsKRTurnerDWailooAComprehensive decision analytical modeling in economic evaluation: a Bayesian approachHealth Econ200413320322614981647
   PubMed Web of Science ®Google Scholar
• CraigBASendiPPEstimation of the transition matrix of a discrete-time Markov chainHealth Econ2002111334211788980
   PubMed Web of Science ®Google Scholar
• DabrowskaDMHoWTConfidence bands for comparison of transition probabilities in a Markov chain modelLifetime Data Anal20006152110763558
   PubMed Web of Science ®Google Scholar
• DebosscherAUnifying stochastic Markov process and its transition probability density functionPhys Rev A19914412792979389905942
   PubMed Web of Science ®Google Scholar
• DentonFTSpencerBGModeling the age dynamics of chronic health conditions: life-table-consistent transition probabilities and their applicationCan J Aging201534217619325917602
   PubMed Web of Science ®Google Scholar
• DiabyVAdunlinGMonteroAJSurvival modeling for the estimation of transition probabilities in model-based economic evaluations in the absence of individual patient data: a tutorialPharmacoeconomics201432210110824338265
   PubMed Web of Science ®Google Scholar
• GaveauBSchulmanLSMultiple phases in stochastic dynamics: geometry and probabilitiesPhys Rev E Stat Nonlin Soft Matter Phys2006733 Pt 203612416605615
   PubMed Web of Science ®Google Scholar
• GuptaSBhattacharyyaSSonathiVBakuliAMathurAKLeteneuxCTransition probability estimation using repeated sampling from a fitted mixed modelValue Health2014177A326
   Web of Science ®Google Scholar
• GuptaSChattopadhyaySGundaPGeneralized implementation of Em algorithm for estimation of transition probability matrixValue Health2015187A694
   Web of Science ®Google Scholar
• HawkinsDLHanCPEstimating transition probabilities from aggregate samples plus partial transition dataBiometrics200056384885410985225
   PubMed Web of Science ®Google Scholar
• HealyBCEnglerDModeling disease-state transition heterogeneity through Bayesian variable selectionStat Med20092891353136819206077
   PubMed Web of Science ®Google Scholar
• HuangGHIntegrated analysis of incidence, progression, regression and disappearance probabilitiesBMC Med Res Methodol200884018577235
   PubMed Web of Science ®Google Scholar
• IacobelliSCarstensenBMultiple time scales in multi-state modelsStat Med201332305315532724027131
   PubMed Web of Science ®Google Scholar
• KassteeleJvHoogenveenRTEngelfrietPMBaalPHBoshuizenHCEstimating net transition probabilities from cross-sectional data with application to risk factors in chronic disease modelingStat Med201231653354322139860
   PubMed Web of Science ®Google Scholar
• KaushikACellerBGAmbikairajahEA methodology to monitor the changing trends in health status of an elderly person by developing a Markov modelConf Proc IEEE Eng Med Biol Soc200522171217417282661
   PubMedGoogle Scholar
• LiZPackSAn application of Markov models in estimating transition probabilities for postmenopausal women with osteoporosisDrug Info J20043814146
   Google Scholar
• LimwattananonCLimwattananonSConstructing a state-transition model for an economic evaluation of cancer treatmentsJ Med Assoc Thai201497Suppl 5S108S112
   Google Scholar
• McCombsJSPharmacoeconomics: what is it and where is it going?Am J Hypertens1998118 Pt 2112S119S discussion 135S–137S9717852
   PubMed Web of Science ®Google Scholar
• MeidaniHGhanemRUncertainty quantification for Markov chain modelsChaos201222404310223278037
   PubMed Web of Science ®Google Scholar
• Meira-MachadoLde Una-AlvarezJCadarso-SuarezCNonparametric estimation of transition probabilities in a non-Markov illness-death modelLifetime Data Anal200612332534416917736
   PubMed Web of Science ®Google Scholar
• Meira-MachadoLde Una-AlvarezJCadarso-SuarezCAndersenPKMulti-state models for the analysis of time-to-event dataStat Methods Med Res200918219522218562394
   PubMed Web of Science ®Google Scholar
• MillerDKHomanSMDetermining transition probabilities: confusion and suggestionsMed Decis Making199414152588152357
   PubMed Web of Science ®Google Scholar
• MilneRJPharmacoeconomic models in disease management. A guide for the novice or the perplexedDis Manag Health Outcomes199843119134
   Google Scholar
• MoussaMAHathoutHKasraouiRSalehAKMeasuring the change in contingency tables using Markov models application to the effect of preceding conception on the next oneMethods Inf Med198221131337057716
   PubMed Web of Science ®Google Scholar
• MuenzLRRubinsteinLVMarkov models for covariate dependence of binary sequencesBiometrics1985411911014005390
   PubMed Web of Science ®Google Scholar
• NagylakiTThe distribution of sojourn times in finite absorbing Markov chainsMath Biosci1976281–26972
   Google Scholar
• NeineMBriquetBMokdadCEVataireALAballeaSBayesian calibration method to estimate transition probabilities for a Markov model based on a continuous outcome measure: application in Parkinson’s diseaseValue Health2013167A325A326
   Web of Science ®Google Scholar
• NgETCookRJModeling two-state disease processes with random effectsLifetime Data Anal1997343153359503879
   PubMedGoogle Scholar
• O’MahonyJFNewallATvan RosmalenJDealing with time in health economic evaluation: methodological issues and recommendations for practicePharmacoeconomics201533121255126826105525
   PubMed Web of Science ®Google Scholar
• OppeMAlMRutten-van MolkenMComparing methods of data synthesis: re-estimating parameters of an existing probabilistic cost-effectiveness modelPharmacoeconomics201129323925021142288
   PubMed Web of Science ®Google Scholar
• PaesATde LimaACA SAS macro for estimating transition probabilities in semiparametric models for recurrent eventsComput Methods Programs Biomed2004751596515158048
   PubMed Web of Science ®Google Scholar
• PutterHFioccoMGekusRBTutorial in biostatistics: competing risk and multi-state modelsStat Med200726112389243017031868
   PubMed Web of Science ®Google Scholar
• RegnierEDShechterSMState-space size considerations for disease-progression modelsStat Med201332223862388023609629
   PubMed Web of Science ®Google Scholar
• Rodriguez-GirondoMde Una-AlvarezJA nonparametric test for Markovianity in the illness-death modelStat Med201231304416442722975898
   PubMed Web of Science ®Google Scholar
• Rodriguez-GirondoMde Una-AlvarezJTesting Markovianity in the three-state progressive model via future-past associationBiom J201254216318022522376
   PubMed Web of Science ®Google Scholar
• Rodriguez-GirondoMUna-AlvarezJdMethods for testing the Markov condition in the illness-death model: a comparative studyStat Med201635203549356226990971
   PubMed Web of Science ®Google Scholar
• RosychukRJShengXStuberJLComparison of variance estimation approaches in a two-state Markov model for longitudinal data with misclassificationStat Med200625111906192116220512
   PubMed Web of Science ®Google Scholar
• RosychukRJThompsonMEBias correction of two-state latent Markov process parameter estimates under misclassificationStat Med200322122035205512802821
   PubMed Web of Science ®Google Scholar
• Saint-PierrePCombescureCDauresJPGodardPThe analysis of asthma control under a Markov assumption with use of covariatesStat Med200322243755377014673936
   PubMed Web of Science ®Google Scholar
• SpitoniCVerduijnMPutterHEstimation and asymptotic theory for transition probabilities in Markov renewal multi-state modelsInt J Biostat2012812322944722
   PubMedGoogle Scholar
• TattarPNVamanHJTesting transition probability matrix of a multi-state model with censored dataLifetime Data Anal200814221623017874296
   PubMed Web of Science ®Google Scholar
• TattarPNVamanHJThe k-sample problem in a multi-state model and testing transition probability matricesLifetime Data Anal201420338740323722306
   PubMed Web of Science ®Google Scholar
• TitmanACTransition probability estimates for non-Markov multi-state modelsBiometrics20157141034104126148652
   PubMed Web of Science ®Google Scholar
• TsangKPWangBCMGarrisonLEstimating Markov chain transition matrices in limited data samples: A Monte Carlo experimentValue Health2012154A164A165
   Web of Science ®Google Scholar
• WeltonNJAdesAEEstimation of Markov chain transition probabilities and rates from fully and partially observed data: uncertainty propagation, evidence synthesis, and model calibrationMed Decis Making200525663364516282214
   PubMed Web of Science ®Google Scholar

Disclosure

HCS is a permanent employee of Takeda Pharmaceuticals International AG. EO, KKC, EH, and DT have received consulting fees from Takeda Pharmaceuticals International AG. The authors report no other conflicts of interest in this work.