Adhesion of osteoblasts to a nanorough titanium implant surface

Abstract

This work considers the adhesion of cells to a nanorough titanium implant surface with sharp edges. The basic assumption was that the attraction between the negatively charged titanium surface and a negatively charged osteoblast is mediated by charged proteins with a distinctive quadrupolar internal charge distribution. Similarly, cation-mediated attraction between fibronectin molecules and the titanium surface is expected to be more efficient for a high surface charge density, resulting in facilitated integrin mediated osteoblast adhesion. We suggest that osteoblasts are most strongly bound along the sharp convex edges or spikes of nanorough titanium surfaces where the magnitude of the negative surface charge density is the highest. It is therefore plausible that nanorough regions of titanium surfaces with sharp edges and spikes promote the adhesion of osteoblasts.

Keywords:

• osteoblasts
• nanostructures
• adhesion
• titanium implants
• osteointegration

Introduction

The cell and tissue response to the composition of an implant surface, and especially to its chemical and physical features, ultimately determines the clinical success of the implant.¹ The functional activity of cells in contact with a biomaterial is determined by the material characteristics of the surface, as well as by the surface topography.² The most widely used material in a gamut of medical applications is titanium,¹ because it is nontoxic and is not rejected by the body. Principally, titanium owes its excellent biostability and biocompatibility characteristics to the thin, hard, adherent titanium dioxide film naturally formed on its surface.

Osteoblast/titanium adhesion depends on the surface characteristics of titanium which may be described according to local mesoscale, microscale, and nanoscale patterns of topography, charge distribution, and chemistry.^3–11 In the past, different studies of implant surface modification have been performed mainly at the micrometer scale in order to improve the attachment of osteoblasts (bone-forming cells) to the implant surface.^3,12–15 Recently, the titanium surface was modified by a self-assembled layer of vertically oriented TiO₂ nanotubes with diameters between 15 nm and 100 nm.¹⁶ It was shown that adhesion, spreading, growth, and differentiation of cells on such vertically aligned TiO₂ nanotube surfaces depend on the diameter of the nanotubes.¹⁶ A nanotube diameter of 15 nm seemed (Figure 1) to be more appropriate for differentiation of mesenchymal, endothelial, and smooth muscle cells in comparison to 70–100 nm nanotubes and to amorphous (smooth) TiO₂ surfaces.¹⁷ These results indicate that the surface nanostructure of an implant is a decisive factor in surface cell adhesion and growth, and is not confined to a specific cell type.^17,18 In line with these results, it has been shown recently that decreased width of the nanorough regions resulted in a significant reduction in the number of osteoblast cells adhering to the structured surface.¹⁹ Osteoblast morphology in the smallest nanorough region was rounder and had less diffuse F-actin filaments, while filopods extending from the cells remained near their origin.¹⁹ The above-mentioned findings are valid generally for the cell response to different topographical nanorough surfaces,^16,19–21 and could in the future have an important impact on the design and composition of implant surfaces. Therefore, these findings must be connected to the increased strength of attractive interactions per unit area in nanorough implant surfaces.

Figure 1 Electron microscope images of the surfaces of vertically aligned TiO₂ nanotubes of 15 nm diameter. The inner and outer diameter of a small diameter nanotube are approximately 10 and 15 nm.

The question of how cells detect and respond to the nanofeatures of an implant surface is still largely unresolved. ⁶ In this work we suggest that the increased surface charge density and electric field strength at highly curved edges of a titanium nanorough surface^16,19–21 (such as a rectangular vertically oriented TiO₂ nanotube surface) could make a major contribution to the increased strength of osteoblast adhesion. The proposed explanation is based on a recently suggested mechanism of protein mediated attractive interaction between a negatively charged titanium surface and negatively charged osteoblasts,¹⁵ as well as on cation-mediated binding of fibronectin.²² Therefore the electric field strength near the highly curved edge of a titanium surface was estimated in the limit of very sharp edges. Then, equilibrium and dynamic models were constructed to test the effects of integrin molecule-binding energy, aggregation energy, and intrinsic curvature on the integrin-mediated adhesion of osteoblasts to nanorough and smooth titanium surfaces.

Adhesion of proteins to a titanium surface

When we discuss osteoblast surface interactions, it ultimately concerns an interaction between osteoblasts and surface-bound proteins or other biomolecules.¹¹ It was recently suggested that the contact between the membrane of the osteoblasts and the titanium surface is established in two steps. Firstly, the osteoblast cell membrane makes a nonspecific contact due to electrostatic forces,¹⁵ followed by a second step where specific binding involving integrin assembly into focal contacts takes place.^16,23,24

Since osteoblasts are negatively charged,²⁵ they are electrostatically repelled by the negatively charged titanium surface as long as some other attractive forces are not present in the system. Recently, a possible mechanism of osteoblast adhesion to the implant surface was proposed on the assumption that positively charged proteins^25,26 or proteins with positively charged tips, ie, a quadrupolar internal charge distribution¹⁵ attached to the negatively charged implant surface, serve as a substrate for the subsequent attachment of negatively charged osteoblasts. In order to predict the orientation of proteins with positively charged tips near a charged implant surface, Monte Carlo simulations of the distribution and the orientation of charged spheroidal proteins in the vicinity of a charged titanium surface were performed.¹⁵ It was shown that for high enough absolute values of the charge density of the titanium surface, the proteins with positively charged tips are concentrated close to the charged surface and oriented in a direction perpendicular to the charged surface¹⁵ (Figure 2A). It was also shown that a high negative surface charge density of the titanium surface and a high effective quadrupolar moment of the protein (ie, distinctive internal quadrupolar charge distribution) can turn the repulsive force between negatively charged Ti and osteoblast surfaces into an attractive force.¹⁵ The corresponding attractive force is also called the bridging force.^15,27 The origin of attractive interactions between two negatively charged surfaces lies in the electrostatic attraction between the positively charged domains on the tips of the titanium surface-bound proteins and the negative charges of the opposite osteoblast membrane (Figure 2B).^15,27

Figure 2 (A) Schematic figure of the orientation of quadrupolar proteins with positively charged tips attached to a negatively charged titanium surface.¹⁵ (B) Schematic figure of a quadrupolar protein mediated attraction between a negatively charged titanium implant surface (left) and a negatively charged osteoblast surface (see also).¹⁵ Two adjacent negatively charged titanium and osteoblast surfaces without bound proteins with a quadrupolar internal charge distribution end repel each other, while for a high enough concentration of bound proteins with a quadrupolar internal charge distribution the force between two negatively charged surfaces becomes strongly attractive,¹⁵ leading to an equilibrium distance approximately equal to the dimension of the proteins.

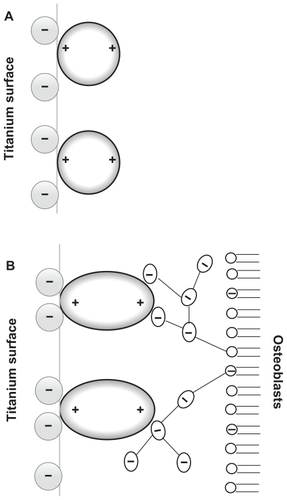
Nonzero effective internal quadrupolar charge distribution does not exclude the presence of other charged protein groups (usually in pairs of positive and negatively charged groups) between the two positively charged protein tips. A typical example of such a bridging protein with positively charged tips is β2-GPI protein which may induce strong attraction between negatively charged surfaces.^27,28

In accordance with the above suggested mechanism of protein-mediated interaction between negatively charged osteoblasts and a negatively charged titanium surface, many studies in the past indicated that increased negative surface potential of the titanium implant promotes osteoblast adhesion and consequently new bone formation.^25,29,30

In line with the predicted increased strength of protein-mediated bridging attractive interaction between a titanium surface and an osteoblast with an increased surface charge density (and electric field strength),¹⁵ we propose that the increased surface charge density and increased electric field strength at the sharp edges of a nanorough titanium surface may promote protein-mediated adhesion of osteoblasts due to the increased accumulation of proteins with quadrupolar internal charge distribution (Figure 3A).

Figure 3 (A) Schematic figure of the adhesion of proteins with quadrupolar internal charge distribution at the sharp edge of a titanium surface. Due to the internal quadrupolar charge distribution, the proteins exhibit strong orientation in the direction of the surface normal vector (see also).¹⁵ (B) Schematic figure of divalent cation-mediated adhesion of negatively charged fibronectin molecules to the highly curved edge of a titanium surface.

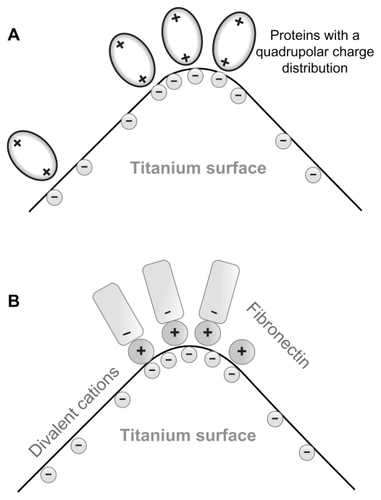
The increased electric field strength and surface charge density of nanorough titanium regions with sharp edges and spikes may also promote divalent cation-mediated adsorption of fibronectin to a negatively charged titanium surface, and in this way also the integrin-mediated adsorption of cells to these titanium regions. Fibronectin is an extracellular glycoprotein with a critical role in the process of cell adhesion.²² A hallmark of fibronectin function is its characteristic assembly into filaments and fibers to form an insoluble matrix which functions as a scaffolding onto which extracellular domains of integrin molecules from the cell membrane are attached³¹ (see also).³² Fibronectin is negatively charged at physiological values of pH.³³ The increase in salt concentration leads to a reduced electrostatic repulsion between the fibronectin and the negatively charged surface.²² Studying the effect of some divalent metallic cations revealed an enhancement of fibronectin adsorption to a negatively charged mica surface.²² The origin of this effect may be bridging and direct interaction forces.^22,29,34,35 Accordingly, it was indicated recently that an increase in the negative net charge of a titanium surface promotes the fibronectin-mediated binding of osteogenic cell receptors.³⁶ All these results suggest that a negatively charged titanium surface can play a prominent role in the osteointegration of metallic implant materials.³⁶ We therefore propose that as a result of the increased electric field strength and increased surface charge density at sharp edges and spikes of various nanorough titanium surfaces, the divalent cation-mediated adhesion of fibronectin is increased (Figure 3B). However, since the surface charge density at very sharp edges of a nano-rough titanium surface could be very high, due to the dramatic increase of the corresponding coupling constant, monovalent cations could also not be excluded as bridging ions.³⁴

To conclude, our suggestion is that the increased surface charge density and corresponding electric field strength at the highly curved edges of a nanorough titanium surface is important for the efficient adhesion of cells. Based on the above arguments indicating the importance of the surface charge density and the electric field strength of a titanium surface in cell adhesion to the titanium surface, in the following the surface charge density and electric field strength are estimated for different curvatures of sharp edges on a titanium surface.

Electric field strength at highly curved edges of a titanium surface

In this section the edge of a titanium surface is considered in the limit of very high curvature. For simplicity, we assume that the curvature of the metal surface in a perpendicular direction along the contour is constant. Then the convex edges of finite curvature are also considered by taking into account water ordering and the finite size of ions as well.

Convex case

In the limit of a very high curvature of a convex edge (Figure 4a), which mathematically represents a singularity, the general solution of the Laplace equation in cylindrical coordinates r and ϕ:³⁷

Figure 4 (A) Schematic figure of the convex edge of a titanium surface in the limit of a very high curvature. (B) Schematic figure of the concave edge (corner) of a titanium surface in the limit of a very high curvature.

$\frac{{\partial }^2\phi }{\partial r^2}+\frac{1}{r}\frac{\partial \phi }{\partial r}+\frac{1}{r^2}\frac{{\partial }^2\phi }{\partial {\varphi }^2}=0.$(1)

$\phi (r,\varphi )={\phi }_0+\sum _{m=1}^{\infty }{A}_m{r}^{2m/3}\text{sin}(2m\varphi /3),$(2)

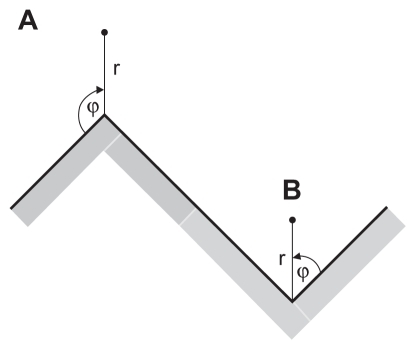
where we took into account the equilibrium (boundary) conditions (the electric potential is constant over the whole conducting metal surface), ie, φ = φ₀ for all r ≥ 0 when ϕ = 0 and ϕ = 3π/2 (see also Figure 4A). In the close vicinity of the edge (where r = 0), ie, for small enough values of r, only the first term of the infinite sum in Eq. (2)$\phi (r,\varphi )={\phi }_0+\sum _{m=1}^{\infty }{A}_m{r}^{2m/3}\text{sin}(2m\varphi /3),$(2) is important. Hence, near r = 0 (Figure 4A) the electric potential is approximately (up to the first order term):

$\phi (r,\varphi )={\phi }_0+A_1{r}^{2/3}\text{sin}(2\varphi /3),$(3)

where A₁ is a constant which can be determined from the additional boundary condition. For σ< 0 the value of A₁ > 0. The electric field strength E = −∇φis:

$\mathbf{E}=-\frac{2A_1}{3}\frac{1}{r^{1/3}}(\text{sin}(2\varphi /3){\mathit{e}}_r+\text{cos}(2\varphi /3){\mathit{e}}_{\varphi }),$(4)

where e_r and e_ϕ are unit vectors. It can be seen from Eq. (4)$\mathbf{E}=-\frac{2A_1}{3}\frac{1}{r^{1/3}}(\text{sin}(2\varphi /3){\mathit{e}}_r+\text{cos}(2\varphi /3){\mathit{e}}_{\varphi }),$(4) that the electric field diverges at the surface edge (r → 0) and then decreases with distance from the edge and distance from the surface. The dependence of the electric field along the symmetry axis (ϕ = 3π/4) is:

$\mathbf{E}(\varphi =3\pi /4)=-\frac{2A_1}{3}\frac{1}{r^{1/3}}{e}_r.$(5)

It follows from the boundary conditions at both metal surfaces and Eq. (4)$\mathbf{E}=-\frac{2A_1}{3}\frac{1}{r^{1/3}}(\text{sin}(2\varphi /3){\mathit{e}}_r+\text{cos}(2\varphi /3){\mathit{e}}_{\varphi }),$(4) that the surface charge densities at both surfaces, ie, at ϕ = 0 and at ϕ = 3π/2 (for r ≥ 0 close to r = 0), are equal to:

$\begin{array}{l}\sigma (r)={\varepsilon }_r{\varepsilon }_0{E}_{\text{n}}(r,\varphi =0)={\varepsilon }_r{\varepsilon }_0{E}_{\text{n}}(r,\varphi =3\pi /2)\\ =-\frac{2A_1}{3}\frac{{\varepsilon }_r{\varepsilon }_0}{r^{1/3}}.\end{array}$(6)

This means that the surface charge density σ(r) is finite at both metal surfaces forming the edge, but becomes singular as r → 0 (ie, at the edge), similar to the electric field. To conclude, the surface charge density is very large (infinite) at the infinitely sharp metal edge and then decreases along both surfaces with increasing distance from the edge.

Concave case

A similar procedure as in the case of a convex edge for a concave edge (ie, corner) in the limit of very high curvature (Figure 4B) gives the dependence of electric field along the symmetry axis (ϕ = π/4):

$\mathbf{E}(\varphi =\pi /4)=-2A_{1}r{\mathbf{e}}_r$(7)

and the surface charge densities at the two surfaces forming the corner, ie, at ϕ = 0 and at ϕ = π/2 in the close vicinity of the corner:

$\sigma (r)=-2A_1{\varepsilon }_r{\varepsilon }_{0}r.$(8)

This means that at an infinitely sharp corner (concave edge), the surface charge density σis zero and then increases with increasing distance from the corner along both surfaces. This explains why the electric field strength increases along the symmetry axis as a function of the distance from the corner (Eq. (7)$\mathbf{E}(\varphi =\pi /4)=-2A_{1}r{\mathbf{e}}_r$(7) ).

For finite values of the curvature radius of the convex edge or the concave edge (corner), the above-described effect of variation of σ over the metal surface is expected to be less pronounced (see next subsection), ie, the surface charge density of the convex edge would not diverge and would decrease in magnitude with the increasing curvature radius. In contrast, the surface charge density and the electric field strength would monotonously increase with increasing curvature radius of the corner (concave edge).

Finite curvature

As shown in the previous two subsections, sharp titanium edges mathematically represent a singularity. Yet, no physical object has perfect corners but some degree of roundness. Therefore, in this subsection the sharp edges are modeled as highly curved convex regions of different radius. The contact of water with biological surfaces has a profound influence on both the thermodynamics and kinetics at biointerfaces; therefore it is a safe prediction that it will be a major topic in biological surface science for a decade or more ahead.¹¹ Hence, we consider a titanium surface in contact with an electrolyte solution where the orientational ordering of water near the implant titanium surface is also taken into account.^38–41

Next, we calculated the electric field at the highly curved edge of constant curvature radius R, which is a generalization of the model presented in the previous subsections (see also Figure 4). We solved numerically the Langevin–Bikerman equation (Eq. (B.7)$\nabla ·[{\varepsilon }_0{\varepsilon }_r(\mathbf{r})\nabla \phi (\text{r})]=-{\rho }_{free}(\mathbf{r}),$(B.7) ), given in Appendix B by using the Comsol Multiphysics 3.5a Software program package (Stockholm, Sweden), by taking into account the boundary conditions Eq. (B.5)$\nabla \phi (\text{r}\to \infty )=0.$(B.5) and Eq. (B.10)$\nabla \phi (\mathbf{r}={\mathbf{r}}_{surf})=-\frac{\sigma \mathbf{n}}{{\varepsilon }_0{\varepsilon }_{\text{r}}(\mathbf{r}={\mathbf{r}}_{surf})},$(B.10) (see Appendix B). However, unlike the planar case solved in Appendix B, to avoid numerical problems the relative permittivity ɛ_r (r), in general defined by Eq. (B.9)${\varepsilon }_r(\mathbf{r})=1+n_{0w}{n}_s\frac{p_o}{{\varepsilon }_o}\frac{F(p_{0}E\beta )}{EH(\phi ,E)}.$(B.9) from Appendix B, was here approximated by a step function with the value ɛ_or in the region r_surf ≤ r ≤ (r + a), where ɛ_or was calculated for the corresponding value of σ (given for the region far away from the edge) from Eq. (B.9)${\varepsilon }_r(\mathbf{r})=1+n_{0w}{n}_s\frac{p_o}{{\varepsilon }_o}\frac{F(p_{0}E\beta )}{EH(\phi ,E)}.$(B.9) for planar geometry at x = 0 (see Figure B.2). In the region r ≥ (r + a) we assumed the bulk value of permittivity, ie, 78.5.

In accordance with the results in the previous subsections (calculated in the limit of very high curvature of the edge), it can be seen in Table 1 that the calculated surface charge density at the top of the surface of the convex titanium edge (σ_top) in the direction of the symmetry axis ϕ = 3π/4 (see also Figure 4A) increases with increasing curvature of the edge 1/R, where R is the curvature radius. On the contrary, in the concave case (corner) (see also Figure 4A), exactly the opposite behavior is observed. This may explain why the cells are most strongly bound along the sharp convex edges or spikes of nanostructured titanium surfaces¹⁹ where the surface charge density and electric field strength are the highest. Also this may offer a possible explanation for the increased divalent cation-mediated fibronectin adhesion and quadrupolar protein-mediated adhesion of an osteoblast on vertically aligned TiO₂ 15 nm nanotubes with respect to the adhesion to a smooth titanium surface.^16–18

Table 1 Comparison of the surface charge densities at the top of a surface of the convex titanium edge (σ_top) in the direction of the symmetry axis ϕ = 3π/4 (see also Figure 4A) and at the corner of a concave surface (σ_cor) in the direction of the symmetry axis ϕ = π/4 (see also Figure 4B) calculated for different values of the edge (corner) curvature radius (R) as described in the text

R/nm	σtop/(As/m^2)	σcor/(As/m^2)
1.0	−0.220	−0.179
2.0	−0.210	−0.189
3.0	−0.207	−0.193
∞	−0.200	−0.200

Notes: Based on the results presented in Figure B.2, we chose values a = 0.3 nm and ɛ_or = 54.481 for surface charge density σ = −0.2 As/m² in the flat region far away from the edge (corner). The values of other model parameters are: p₀ = 5D, n₀/N_A = 0.15 mol/L and n_0w/N_A = 55 mol/L.³⁹

Clustering of integrin molecules in nanorough titanium regions with highly curved edges

Previous studies have been shown that decreasing the width of the nanorough regions¹⁹ or a reducing the degree of nanostructuration of the titanium surface^16–18 significantly reduced the number of osteoblast cells adhering to the structured surface. Yet the underlying mechanism that drives the adhesion of a cell membrane to nanorough titanium regions is not fully clear.

In what follows, a dynamic model is constructed to test the effects of the binding energy, aggregation energy, and spontaneous curvature of membrane inclusions (eg, integrins) on adhesion to nanorough titanium surfaces. In our model, the key function of the membrane inclusions is their capacity to stabilize and induce membrane protrusions, while the negative adhesion energy drives the initial growth of membrane protrusions.

Previous theoretical studies demonstrated that the aggregation of membrane inclusions of positive intrinsic curvature (ie, outward membrane bending) can be coupled to membrane protrusive forces originating from the adhesion to the extracellular matrix and from the polymerization of actin filaments.^15,42 This theory is based on previous experimental data revealing that a large family of curved membrane proteins, for example, those containing Bin/Amphiphysin/Rvs (BAR) and IRSp53-Missing-In-Metastasis (IMD) domains, can induce concave or convex curvatures.⁴⁴ Furthermore, these curved proteins may form membrane-bound complexes that include actin-nucleating components,^45,46 which have been observed to induce cellular protrusions.^47,48

Above, it is suggested that due to an increased surface charge density and increased electric field strength at sharp edges and spikes of nanorough titanium surfaces, the cation-mediated adhesion of fibronectin is increased (Figure 3B). The increased fibronectin accumulation in the nanorough regions of a titanium surface with an increased surface charge density and increased electric field strength can facilitate the adhesion and aggregation of integrin molecules and therefore can induce the formation of focal adhesion complexes.³² In the following, we present a simple equilibrium model of the aggregation and adhesion of integrin molecules in order to implicitly model nanorough titanium regions with highly curved edges (Figure 5).

Figure 5 Schematic figure of two regions of a titanium surface: nanorough region 1 with high affinity for integrin molecules, and a smooth region 2 with low affinity for integrin molecules.

Equilibrium model

The basic assumption of our model is that integrin molecules which adhere on the nanostructured (nanorough) regions (region 1) of a titanium surface with an increased surface charge density and an increased density of bound fibronectins are in equilibrium with those integrin molecules in regions with a lower surface charge density (and lower electric field strength) and a lower area density of bound fibronectin molecules (region 2) (Figure 5).

The Helmholtz free energy of integrin molecules in the first (i = 1) and second region (i = 2) can be derived within lattice statistics from the corresponding canonical partition function F_i = −kT lnQ_i (see also):^49,50

$\begin{array}{l}{F}_i=-N_i{w}_i-\frac{c\mathrm{\Omega }{N}_i^2}{2M_i}+{\mathit{kTN}}_i\hspace{0.17em}\text{ln}\left(\frac{N_i}{M_i}\right)\\ +kT(M_i-N_i)\text{ln}\left(1-\frac{N_i}{M_i}\right),i=1,2,\end{array}$(9)

where

$Q_i=\frac{M_i!}{N_i!(M_i-N_i)!}\text{exp}(N_i{w}_i)/kT)\text{exp}({cN}_i^2{\mathrm{\Omega }}_i/2M_{i}kT).$(10)

Here −w_i is the negative binding energy of a single integrin molecule in the i-th region (w_i > 0), Ω_i is the direct-interaction (attraction) Bragg–Williams constant (Ω_i > 0), c is the number of the nearest neighbor integrin molecules, kT is the thermal energy, N_i is the number of integrin molecules in the i-th region and M_i is the number of lattice sites in the i-th region. It is then assumed that M_i >> N_i, and, as a result, the chances of interaction between integrin molecules is small and Ω_i becomes zero. It is also assumed that w₁ > w₂. The system free energy F_tot = F₁ + F₂ is:

$\begin{array}{l}\frac{F_{tot}}{MkT}=-{\phi }_1{n}_1\frac{w_1}{kT}+{\phi }_1{n}_1\hspace{0.17em}\text{ln}\hspace{0.17em}{n}_1+{\phi }_1(1-n_1)\text{ln}(1-n_1)\\ -{\phi }_2{n}_2\frac{w_2}{kT}+{\phi }_2{n}_2\hspace{0.17em}\text{ln}\hspace{0.17em}{n}_2+{\phi }_2(1-n_2)\text{ln}(1-n_2)\end{array}$(11)

and minimization with respect to n₁ yields:

$\frac{(1-n_1)(n_0-\mathrm{\Phi }{n}_1)}{n_1(1-n_0+\mathrm{\Phi }{n}_1)}={\beta }_w,$(12)

where n₁ = N₁/M₁ and n₂ = N₂/M₂ are the relative densities of integrin molecules in region 1 with strong adhesion and region 2 with weak adhesion, respectively, ϕ_i = M_i/M, M = M₁ + M₂, Φ = φ₁/φ₂ = M₁/M₂, Δw = w₁ − w₂ and ${\beta }_w=\text{exp}\hspace{0.17em}(-\frac{\mathrm{\Delta }w}{kT})$. In the above minimization procedure, the conservation equation for the total number of bound integrin molecules N = N₁ + N₂ was taken into account in the form:

$\mathrm{\Phi }{n}_1+n_2=n_0,$(13)

where n₀ = N/M₂. Using the definition B = Φ + β_w + n₀ − n₀β_w, the solution of Eq. (12)$\frac{(1-n_1)(n_0-\mathrm{\Phi }{n}_1)}{n_1(1-n_0+\mathrm{\Phi }{n}_1)}={\beta }_w,$(12) is given in the form:

$n_1=\frac{B-{(B^2-4M_1{n}_0(1-{\beta }_w)/M_2)}^{1/2}}{2M_1(1-{\beta }_w)/M_2}.$(14)

Eq. (14)$n_1=\frac{B-{(B^2-4M_1{n}_0(1-{\beta }_w)/M_2)}^{1/2}}{2M_1(1-{\beta }_w)/M_2}.$(14) predicts an increase of n₁ with increasing Δw. In the limit of very large Δw (when β_w → 0), ie, in the limit of very strong binding in the nanorough region 1, Eq. (14)$n_1=\frac{B-{(B^2-4M_1{n}_0(1-{\beta }_w)/M_2)}^{1/2}}{2M_1(1-{\beta }_w)/M_2}.$(14) predicts the complete accumulation of integrin molecules in region 1: n₁ → N/M₁.

Dynamic model

To shed light on the dynamics of membrane growth on nanorough titanium surfaces (eg, TiO₂ nanotubes), we constructed a model based on the Helfrich free energy, which also included the binding energy of integrin molecules to the titanium surface, as well as the nearest-neighbor attractive interaction energies between integrin molecules. The difference from the equilibrium model is that in the dynamic model we take into account the direct-interaction Bragg–Williams term and membrane bending energy. Unlike the equilibrium model, the nonhomogeneous lateral distribution of integrins of explicitly modeled. The intrinsic shape of the integrin molecules is taken into account in the spontaneous curvature of the Helfrich expression for membrane bending energy.

The model described below is an extension of previous theoretical models.^15,42,43,51 The basic equations of motion of the membrane contour and the time dependence of the nonhomogeneous lateral density of integrin molecules are derived in Appendix A.

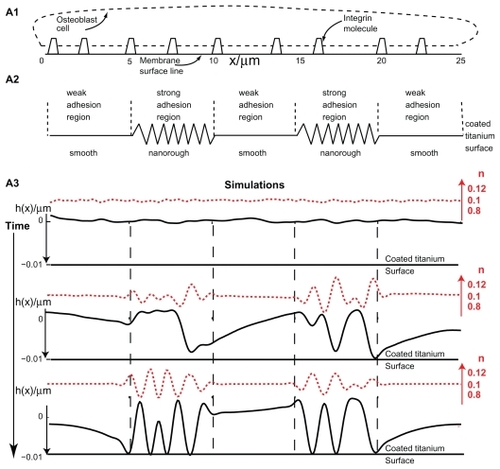
The shapes explored in this model describe a segment of the cell (osteoblast) outer contour, where the membrane is initially flat (Figure 6). This modeled membrane geometry is under the constraint of translational symmetry. Moreover, we assume that the membrane curvature along the perpendicular direction of the contour is roughly constant, and thus enters our calculation as a modified membrane tension. We take into account only a segment of the osteoblast cell contour (Figure 6). The nanorough and smooth titanium surfaces are both modeled as flat surfaces, while the influence of their surface topography on the osteoblast binding is implicitly taken into account by considering different binding energy potentials. For the sake of simplicity we assume that the initial protein bridging forces (Figure 2B), as well as the cation-mediated adhesion of integrins (Figure 3B), are much stronger in nanorough regions than in smooth titanium regions (ie, w₁ >> w₂, w₂ = 0, see also previous section) and the binding of integrins is possible only in nanorough regions (Figure 6).

Figure 6 Effects of nanorough and smooth titanium regions on membrane growth. The modeled membrane segment that belongs to an osteoblast cell is a nearly straight membrane contour with embedded integrin molecules (A1). Nanorough titanium regions are separated by smooth titanium regions (A2). The implicit effect of the smooth and nanorough regions is incorporated into the free energy by having a zero integrin binding potential above the smooth titanium regions and nonzero integrin binding potential above the nanorough titanium regions. In addition, it was assumed that the integrin binding potential in the 10 nm thick layer above the nanorough titanium regions for simplicity was constant, ie, w n_s = 0.011 g s⁻². Time dynamics of the membrane shape (h(x)) and integrin density (n) for the adhesion of an osteoblast membrane to the implicitly modelled nanorough regions (A3). Note the coalescence of membrane protrusions over time, and the steady state (bottom panel) adhesion in a small number of patches to the titanium surface.

The titanium surface is modeled as a flat contour to which the osteoblast membrane may adhere (Figure 6). It is assumed that once part of the membrane adheres to the titanium surface, this part of the membrane (ie, the contour coordinates) can no longer be detached from the titanium surface. This trapping prevents further membrane evolution throughout the simulation, and originates in strong electrostatic interactions of the titanium surface with the cell membrane and in the binding of membrane integrins to the titanium surface-attached fibronectin molecules (Figure 7). We assume that in our model the overall number of integrin molecules in the membrane is conserved, and that they are allowed to move laterally along the osteoblast membrane. The maximum possible number of integrin molecules in the membrane segment is obtained from the total area divided by the cross-sectional area of the extracellular region of an integrin molecule.

Figure 7 The protein mediated adhesion of an osteoblast to the nanorough region of a titanium surface is facilitated due to the increased surface charge density and electric field strength at highly curved convex edges and spicules.

Equations of motion

Our model investigates the coupling between the adhesion of osteoblast cells to the extracellular matrix, the interaction between integrin molecules, and their spontaneous curvature. A free energy expression similar to the one explored for the equilibrium model (Eq. (10)$Q_i=\frac{M_i!}{N_i!(M_i-N_i)!}\text{exp}(N_i{w}_i)/kT)\text{exp}({cN}_i^2{\mathrm{\Omega }}_i/2M_{i}kT).$(10) ) is employed to derive the equations of motion of an osteoblast membrane contour and the integrin density distributions. The membrane free energy in our dynamic model is:

$\begin{array}{l}F=\int (\frac{1}{2}\kappa {(H-\overline{H}n)}^2+{\sigma }_t+{\varphi }_s{h}^2-{wn}_{s}n-n_s\frac{c\mathrm{\Omega }}{2}{n}^2\\ +{\mathit{kTN}}_{s}n\hspace{0.17em}\text{ln}(n)+{\mathit{kTN}}_s(1-n)(1-n))\text{dA},\end{array}$(15)

where the first term gives the bending energy due to the mismatch between the membrane curvature and the membrane spontaneous curvature due to embedded integrin molecules, κ is the bending modulus, H is the local membrane mean curvature, H̄ is the intrinsic mean curvature due to embedded integrins and n is the area fraction density of integrins (relative density). The second term (σ_t) is the Lagrange multiplier (having the units of membrane surface tension) for the conservation constraint of the total membrane area. The third term gives the energy due to the force of the cytoskeleton inside the osteoblasts, where ϕ_s is the restoring cytoskeleton spring constant. The fourth term is the negative binding potential of integrin molecules (w > 0). The results of the equilibrium model show that for a large integrin binding potential w, the attraction of integrin molecules towards the nanorough region increases (Eq. (14)$n_1=\frac{B-{(B^2-4M_1{n}_0(1-{\beta }_w)/M_2)}^{1/2}}{2M_1(1-{\beta }_w)/M_2}.$(14) ), causing the depletion of integrins from a nearby smooth region. For simplicity, in the dynamic model it is assumed that the binding energy comes into effect only for those membrane parts above nanorough titanium regions. We consider only the cases where the osteoblast membrane is at a short distance from the titanium surface. In addition, all membrane integrins above nanorough titanium surface regions are assumed to have the same nonzero w. The fifth term in Eq. (15)$\begin{array}{l}F=\int (\frac{1}{2}\kappa {(H-\overline{H}n)}^2+{\sigma }_t+{\varphi }_s{h}^2-{wn}_{s}n-n_s\frac{c\mathrm{\Omega }}{2}{n}^2\\ +{\mathit{kTN}}_{s}n\hspace{0.17em}\text{ln}(n)+{\mathit{kTN}}_s(1-n)(1-n))\text{dA},\end{array}$(15) describes the direct interaction Bragg–Williams term between neighboring integrin molecules. The sixth and seventh terms are the entropic energies, which take into account the finite areas of integrin molecules. Here dA = d_m ds is an infinitesimal membrane area element, d_m is the length of the membrane in the direction perpendicular to the membrane contour,

$\text{ds}={\left({\left(\frac{\partial \text{x}}{\partial \text{u}}\right)}^2+{\left(\frac{\partial \text{y}}{\partial \text{u}}\right)}^2\right)}^{1/2}\text{du}$

is the infinitesimal length of the membrane along the contour in the x − y plane, where u runs from 0 to 1, n is the relative density of integrin molecules (with values between 0 and 1), Ω is the direct-interaction Bragg–Williams constant (Ω > 0), c is the number of the nearest neighbor integrin molecules, h = h(s) describes the magnitudes of small deformations from the flat membrane and n_s = 1/a₀ is the saturation area density of integrin molecules, where a₀ is the cross-section area of a single integrin molecule. The local mean curvature is given by

$H=\frac{{\partial }^{2}y}{\partial s^2}\frac{\partial x}{\partial s}-\frac{{\partial }^{2}x}{\partial s^2}\frac{\partial y}{\partial s}.$

The spontaneous curvature of the membrane C₀ = H̄n is assumed to be proportional to the intrinsic mean curvature of the integrin molecule H̄.

In the following the free energy is normalized with respect to d_m so F/d_m → F, and as a result the free energy is considered to vary along the membrane contour and not in the direction perpendicular to the membrane contour. We next derive the equations of motion of the membrane contour by differentiation of the free energy (Eq. (15)$\begin{array}{l}F=\int (\frac{1}{2}\kappa {(H-\overline{H}n)}^2+{\sigma }_t+{\varphi }_s{h}^2-{wn}_{s}n-n_s\frac{c\mathrm{\Omega }}{2}{n}^2\\ +{\mathit{kTN}}_{s}n\hspace{0.17em}\text{ln}(n)+{\mathit{kTN}}_s(1-n)(1-n))\text{dA},\end{array}$(15) ) with respect to the membrane coordinate¹⁵ and integrin concentration. To take into account the drag due to viscous forces, we assume for simplicity only local frictional forces, with coeffcient ζ. For the nearly flat osteoblast membrane, the equation of motion of the membrane is given by

$\xi \frac{\partial \text{h}(\text{s})}{\partial \text{t}}=-\frac{\delta F(s)}{\delta \text{h}},$(16)

where t is time. Note that the force δF(s)δh equals the membrane shape velocity times the friction coeffcient, but opposite in direction. Since the relative change in the y (ie, vertical, y = h(s)) direction is considerably greater than the change along the x (ie, horizontal) direction, we consider only changes along the vertical y direction.

The details of the membrane contour forces and fluxes derived from the derivation of the free energy, as well as the list of parameter values incorporated in our model, are given in Appendix A.

Strong binding to nanorough regions

While numerous experimental studies have shown that the nanorough regions of a titanium surface implant facilitate the binding of osteoblast cells, the underlying mechanisms are not fully understood. Here it is proposed that nanorough regions cause an increase of electric field strength and an aggregation of charge (as shown above) which enhances the binding of fibronectin and consequently integrin molecules to the titanium implant surface. To investigate the effect of having a distribution of nanorough regions, the effects of increased binding strength are incorporated into the free energy equation using a negative binding energy term, –wn_sn (Eq. (15)$\begin{array}{l}F=\int (\frac{1}{2}\kappa {(H-\overline{H}n)}^2+{\sigma }_t+{\varphi }_s{h}^2-{wn}_{s}n-n_s\frac{c\mathrm{\Omega }}{2}{n}^2\\ +{\mathit{kTN}}_{s}n\hspace{0.17em}\text{ln}(n)+{\mathit{kTN}}_s(1-n)(1-n))\text{dA},\end{array}$(15) ). The same average binding potential energy w is taken into account for all integrins above the nanorough titanium surface.

Our system is driven dynamically by two mechanisms. The first is the instability that leads to the initial growth of membrane protrusions is driven by the interplay between a positive membrane surface tension and a negative binding potential and a direct-interaction energy. The second is the curvature-dependent flow of membrane-embedded integrins into favorable curved membrane regions, thereby reducing the free energy of the system. The above dynamics drive a positive feedback loop in which the influx of integrins towards regions of favorable curvature increases the positive membrane curvature, which then further attracts integrins (see also Eq. (15)$\begin{array}{l}F=\int (\frac{1}{2}\kappa {(H-\overline{H}n)}^2+{\sigma }_t+{\varphi }_s{h}^2-{wn}_{s}n-n_s\frac{c\mathrm{\Omega }}{2}{n}^2\\ +{\mathit{kTN}}_{s}n\hspace{0.17em}\text{ln}(n)+{\mathit{kTN}}_s(1-n)(1-n))\text{dA},\end{array}$(15) ).

In the following numerical simulation it was assumed that the osteoblast membrane was initially positioned 10 nm above a flat titanium surface, where the total length of the membrane was 25 μm. Furthermore, a random perturbation of small amplitude < 1% in integrin density was added around the initial density of the integrin molecules. The condition for instability was satisfied only over the nanorough regions at which initial membrane growth was observed (Figure 6). Along the simulation, larger membrane protrusions were formed by the coalescence of smaller membrane protrusions (Figure 6). The large membrane protrusions eventually adhered to the titanium surface, trapping the adhering membrane regions by the end of the simulation (Figure 6).

To evaluate the effect of a negative binding term, the same simulation as above was run with a larger value for the binding potential w. The results revealed that the time for and the amounts of membrane adhesion to the titanium surface were different. In particular, it was shown that the time scale for the coalescence of membrane protrusions and membrane growth is shorter, and as a result, more membrane regions adhered to the titanium surface, which is due to the increased instability of the model system.^15,42,43

Discussion and conclusions

To understand the role of proteins (such as fibronectins, vitronectins, and laminins) involved in osteoblast adhesion on the surface of a titanium implant is of crucial importance.^3,6 Our basic assumption that the attraction between a negatively charged titanium surface and a negatively charged osteoblast is mediated by charged proteins with a distinctive quadrupolar internal charge distribution¹⁵ may be supported by experimental results. These showed that osteoblasts are flattened so closely onto the positively charged substrata that the ventral cell membrane was not distinguishable under the transmission electron microscope, while on negatively charged substrata the ventral cell membrane was readily visible only with focal contacts with the substrata.^3,5 This indicates that the osteoblasts are strongly bound to the positively charged substrate due to direct electrostatic binding of a negatively charged glycocalyx of an osteoblast membrane to the positive substrate, while the binding of an osteoblast to a negatively charged substrate is mediated by proteins with a distinctive quadrupolar internal charge distribution (Figure 2).

In accordance, it was observed that the protein populations desorbed from a positively charged substrate also differ from the populations described from a negatively charged substrate, indicating that protein adsorption is dependent on the charge of the substratum.⁵ This is not at all surprising as proteins consist of many charged subunits. However, as the majority of proteins at physiological pH carry a net negative charge, a greater number of proteins would have been expected to adsorb to positive substrata.⁵ But in fact it was observed that fewer proteins were desorbed from a positive surface than from a negative surface⁵ which supports our model of binding of proteins with a distinctive quadrupolar internal charge distribution (like proteins with positively charged terminal groups) to a negatively charged substrate (titanium) (Figure 2). Note that a nonzero quadrupolar internal charge distribution of the protein does not exclude the possibility that the protein carries net zero or negative total charge (see also).^27,28

In order to assess the influence of geometrically structured titanium profiles on the surface charge density and electric field at the implant surface, we concentrated on estimation of the electric field at their most convex part. We showed that the surface charge density and electric field strength on the sharp convex metallic surface regions are highly increased.

Based on this result we suggest that nanorough regions, due to their many highly curved nanoscale protrusions and/or edges, have increased surface charge density and electric field strength. The increased surface charge density and electric field strength of such nanorough regions promote divalent cation-mediated adsorption of fibronectin to a negatively charged titanium surface²² and quadrupolar protein mediated adhesion of osteoblasts to a negatively charged titanium surface,^15,27,28 both leading to a more efficient adhesion of osteoblasts to a titanium nanorough surface (Figure 7). In accordance with our model that predicts stronger binding of osteoblasts to highly curved nanoscale protrusions and/ or edges, it was experimentally observed that focal contacts on smooth surfaces were distributed uniformly over the whole membrane surface in contact with the substrate.⁴ However, on rough surfaces, focal contacts were visible only at the extremities of the cell extensions where cell membranes were in contact with the substrate.^3,4

In the present study, lattice statistics of the equilibrium state was employed to demonstrate that in the limit of a large binding potential for integrins in a nanorough region (Eq. (14)$n_1=\frac{B-{(B^2-4M_1{n}_0(1-{\beta }_w)/M_2)}^{1/2}}{2M_1(1-{\beta }_w)/M_2}.$(14) ) there is a strong attraction of integrin molecules towards the nanorough region, and their depletion from nearby smooth regions. Experimentally, a nanorough region could be obtained using various experimental procedures, eg, by the construction of vertically aligned TiO₂ nanotubes. The results of the presented theoretical consideration in equilibrium conditions explain the strong attraction of integrin molecules to the sharp edges of a titanium surface, for example, to the edges of a TiO₂ nanotube surface (Figure 1).

In accordance with our theoretical predictions, it has been shown recently that a decrease in width of nanorough regions (of dimension from 80 μm and 48 μm to 22 μm) resulted in significant reductions in the number of osteoblast cells adhering to the structured surface.¹⁹ It was hypothesized that osteoblasts recognize different surface roughnesses through the interaction of proteins in the extracellular matrix, a supposition which is confirmed in the present work. In another study, it was shown that osteoblasts are responsive to small nanopatterns of length scale below 100 nm in groove width and depth, as detected by the deposition of minerals (eg, hydroxypatite) along these nanosize patterns.⁵² As already mentioned above, the nanorough surfaces of vertically aligned TiO₂ nanotubes (Figure 1) facilitate the adhesion of osteoblasts and other cells with respect to adhesion to a smooth titanium surface.^16–18

To gain more understanding of this behavior, the equilibrium free energy model was extended to explore the dynamics of integrin molecules on a nearly flat membrane segment of a cell (eg, an osteoblast) growing on the surface of implicitly smooth and nanorough titanium regions. The system free energy was constructed to derive the membrane shape dynamics and integrin density distributions while taking into account certain biophysical considerations. Namely, it was assumed that an integrin molecule has a positive (outward bending) intrinsic curvature, since the extracellular part of the integrin molecule is greater in size than its intramembrane part. Secondly, the aggregation of integrin molecules allows close-range interactions thereby reducing the free energy of the system when clusters of integrins are formed during their attachment to the titanium surface. Finally, in the dynamic model the nanorough and smooth regions are implicitly modeled by strong and weak regimes of integrin binding.

The results of our dynamic simulations demonstrate that due to initially stronger electrostatic interactions, the advantage of a nanorough titanium surface over a smooth titanium surface is crucial for the clustering of integrins in the process of adhesion of the osteoblast membrane to the nanorough titanium surface regions (Figure 6). In fact, the growth and adhesion of the cell membrane is mainly within the boundaries of the nanorough regions. The results of our dynamic model show that the membrane does not fully adhere to the titanium surface, which is due to the aggregation of integrin molecules in local membrane regions above the nanorough titanium regions. The amount of membrane adhesion was shown to depend on the binding potential w and nearest neighbor direct interaction energy between integrin molecules.

Recent experimental data revealed that the growth and differentiation of osteoblast cells on small diameter (~15 nm) vertically aligned TiO₂ nanotubes (Figure 1) is substantially greater than on large diameter (100 nm) nanotube surfaces.^16–18 It has been proposed that the observed aggregation of integrin molecules forming focal adhesion is enhanced on small diameter nanotubes because the extracellular part of the integrin molecule is of a similar size, enabling crossbinding over the edges of neighboring nanotubes and over the hollow interiors of vertically oriented TiO₂ nanotubes (Figure 1). In the light of the results of the present study, we suggest that enhanced growth of a cell membrane on a nanotube surface is also facilitated by the interaction of integrin molecules during the formation of a point of focal adhesion (Figure 6). Moreover, the fact that small diameter nanotubes present on average more surface edges (with increased surface charge density and electric field strength) per unit area, the binding affnity of a small diameter nanotube surface is expected to be increased in accordance with the results presented in the present paper.

Many different proteins play a role in the interactions between the implant surface and the osteoblast. In addition to fibronectin (considered in this work), human osteoblasts also adhere to vitronectin⁶ and weakly to laminin.³ The structure of vitronectin, an integrin binding protein, was predicted through a combination of computational methods and experimental approaches.^53,54 Vitronectin is composed of three main structural domains, the N-terminal somatomedin B domain, the central domain, and the C-terminal domain. Like fibronectin, vitronectin also contains an Arg-Gly-Asp (RGD) sequence close to the somatomedin B domain which is responsible for integrin binding and cell adhesion.^3,53 The highly positively charged group of vitronectin near the C-terminal group on the other side of the molecule (largely uninterrupted by negative charges) is the binding site for the negatively charged molecules of heparin.^36,53,54 It can therefore be anticipated that the heparin binding site of vitronectin (positively charged) may be predominantly (electrostatically) bound along the sharp convex edges or spikes of nanorough titanium surfaces where the magnitude of the negative surface charge density of the titanium surface is the highest. On the other hand, the vitronectin RGD binding site on the other side of the vitronectin molecule may bind to the integrin molecule, resulting in facilitation of osteoblast adhesion at sharp convex edges or spikes of nanorough titanium surfaces (in addition to the fibronectin–integrin mediated osteoblast adhesion already described).

In conclusion, the nanostructuring of implant surfaces provides a powerful mechanism to encourage and direct cell adhesion to the implant surface.⁶ Based on the results presented in this work, we suggest that nanorough titanium implant regions, due to their many highly curved nanoscale protrusions and/or edges, have locally an increased surface charge density and electric field strength. The increased surface charge density and electric field strength of such nano rough regions promote divalent cation-mediated adsorption of fibronectin to a negatively charged titanium surface (Figure 3B)²² and quadrupolar protein-mediated adhesion of osteoblasts to a negatively charged titanium surface (Figure 2), both leading to more effcient adhesion and spreading of osteoblasts to a nanorough titanium surface (Figure 7). The suggested mechanism of increased binding of osteoblasts along the sharp convex edges or spikes of nanorough titanium surfaces due to the locally increased magnitude of the negative surface charge density is also valid for other metals (besides titanium) since the accumulation of negative charge at convex edges and spikes also takes place in the case of other metal surfaces.

Acknowledgment

This work was supported by DFG for the project A3 in Research Training Group 1505/1 “welisa” and ARRS grants J3-9219-0381, P2-0232-1538. The authors are grateful for help to Nir Gov from Weizmann Institute of Science.

Disclosure

The authors have no conflicts of interest to disclose in this work.

Appendices

Appendix A: dynamic model of the osteoblast membrane

In this Appendix we give further details of the dynamic model employed to test the effects of integrin mediated adhesion of osteoblasts to nanorough and smooth titanium surfaces. The differentiation of the free energy (Eq. (15)$\begin{array}{l}F=\int (\frac{1}{2}\kappa {(H-\overline{H}n)}^2+{\sigma }_t+{\varphi }_s{h}^2-{wn}_{s}n-n_s\frac{c\mathrm{\Omega }}{2}{n}^2\\ +{\mathit{kTN}}_{s}n\hspace{0.17em}\text{ln}(n)+{\mathit{kTN}}_s(1-n)(1-n))\text{dA},\end{array}$(15) ) is projected to give the forces normal to the membrane contour. We now list the forces derived from the differentiation of the free energy:

$F_{\text{curvature}}=k\left(-{\nabla }^{2}H+\overline{H}{\nabla }^{2}n+\frac{1}{2}{n}^2{\overline{H}}^{2}H+\frac{1}{2}{H}^3\right),$(A.1)

$F_{\text{tension}}={\sigma }_{t}H,$(A.2)

$F_{\text{binding}}=-{wn}_{s}nH,$(A.3)

$F_{\text{spring}}=-2{\varphi }_s\hspace{0.17em}y,$(A.4)

$F_{\text{entropy}}={\mathit{kTN}}_s[n\hspace{0.17em}\text{ln}(n)+(1-n)\text{ln}(1-n)]H,$(A.5)

$F_{\text{interaction}}=-c\mathrm{\Omega }{n}_s{n}^{2}H/2,$(A.6)

where F_curvature is the force due to the curvature energy mismatch between the membrane curvature and the spontaneous curvature of the integrins, F_tension is the membrane tension force, F_binding is the force due to binding of integrin molecules, F_spring is the spring restoring force, F_entropy arises from the entropy of the integrins in the membrane, which acts to expand the length of the contour, and F_interaction is the force due to the direct interaction between neighboring integrin molecules. The nonlinear term H ³/2 in F_curvature is neglected in the following.

We now calculate the dynamics of the integrin density, using the following conservation equation:

$\frac{\partial n}{\partial t}=-\nabla ·\overrightarrow{J}-\frac{\mathrm{\Lambda }}{n_s}\nabla \left(n\nabla \frac{\delta F}{\delta n}\right)-\frac{n}{\text{ds}}\frac{\partial ds}{\partial t},$(A.7)

where Λ is the mobility of filaments and J→ is the total current of integrins on the membrane, which includes the following terms:

$J_{\text{attraction}}=\frac{k\mathrm{\Lambda }\overline{H}}{n_s}n\nabla H,$(A.8)

$J_{\text{dispersion}}=\frac{k\mathrm{\Lambda }{\overline{H}}^2}{n_s}n\nabla n,$(A.9)

$J_{\text{interaction}}=\mathrm{\Lambda }c\mathrm{\Omega }n\nabla n,$(A.10)

$J_{\text{diffusion}}=-D\nabla n,$(A.11)

where J_attraction is the attractive flux resulting from the interaction between the integrins through the membrane curvature, J_dispersion is the dispersion flux due to membrane resistance to integrin aggregation due to their membrane bending effects, J_interaction is the flux due to the direct interaction between integrins, and J_diffusion is the usual thermal diffusion flux which depends on the diffusion coeffcient, D = ΛkT. The last term in Eq. (A.7)$\frac{\partial n}{\partial t}=-\nabla ·\overrightarrow{J}-\frac{\mathrm{\Lambda }}{n_s}\nabla \left(n\nabla \frac{\delta F}{\delta n}\right)-\frac{n}{\text{ds}}\frac{\partial ds}{\partial t},$(A.7) arises from the covariant derivative of the density with time on a contour whose length evolves with time. In this term ds is the infinitesimal contour (line) element. This term ensures that the total number of integrins is conserved as the contour length changes. Note that the fluxes due to entropy were not taken into account due to their relatively small magnitude.

The results in the present study were calculated using numerical simulations of the dynamics of the model system beyond the linear limit. The differential equations explained above were solved using an explicit Euler method in Matlab. We checked for the convergence of our one-dimensional simulations in space and time. A variation of the Monge representation h(s) was employed to simplify the numerics, such that the curvature force was kept only up to linear order. For simplicity, the boundary conditions on the nearly flat membrane were taken to be periodic. The following is the list of parameter values incorporated in our numerical simulations:

$\begin{array}{l}\xi =125\hspace{0.17em}{\text{gs}}^{-1},D=0.002\hspace{0.17em}\mu {\text{m}}^2{\text{s}}^{-1},\mathrm{\Lambda }=D/kT,n_s=100\hspace{0.17em}\mu {\text{m}}^{-2},\\ {\varphi }_s=0.0008\hspace{0.17em}\text{g}\mu {\text{m}}^{-2}{\text{s}}^{-2},k=100\hspace{0.17em}kT,\overline{H}=10\mu {\text{m}}^{-1},\\ {\sigma }_t=0.001\hspace{0.17em}\text{g}{\text{s}}^{-2},w=1.1·{10}^{-4},\text{g}\mu {\text{m}}^2{\text{s}}^{-2},c=4,\\ \mathrm{\Omega }=1.75·{10}^{-5}\hspace{0.17em}\text{g}\mu {\text{m}}^2{\text{s}}^{-2}.\end{array}$

Appendix B:

Langevin-Bikerman model of a charged metallic surface in contact with an electrolyte, considering the finite size of molecules and orientational ordering of water

The contact between a charged titanium surface and an electrolyte solution implies a particular ion distribution near the charged surface, ie, the electrical double layer (EDL).^5,6 The distribution of ions in the EDL can be described within the Poisson-Boltzmann (PB) theory^1,7–10 by expressing the competition between electrostatic interactions and the entropy of ions in the solution. Due to the electrostatic forces between the charged surface and the ions in solution, counterions are accumulated close to the charged surface, while coions are depleted from this region (Figure B.1). As already shown, the properties of the EDL may also be influenced by ordering of water molecules in the region of the electric double layer.^8,11–15

Figure B.1 Schematic figure of an electrical double layer near a negatively charged planar membrane surface. The water molecules in the vicinity of the charged surface are predominantly oriented towards the surface.

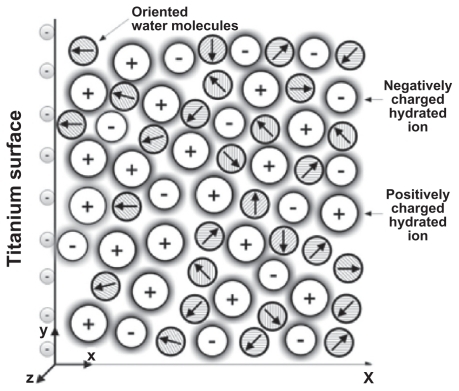
Most of the PB-based models of the EDL^1,7,8,16,17 assume that the relative permittivity in the electrolyte is constant. In the absence of explicit consideration of the orientational ordering of water molecules, the assumption of constant permittivity is largely a consequence of the constant number of water molecules in PB theory. But actually, close to the charged surface the orientation of water molecules (Figure B.1) may result in a spatial variation of permittivity.^13,18–20 Considering this effect, the EDL mean-field theory was modified by orientational ordering of water molecules where the water molecules were described as Langevin dipoles,^{2–4,18,19,21} which may be considered to be a very rough treatment of the relative properties of the solvent.^22–24 Taking into account the finite volume of ions and water orientation,^1–3 the electric potential can be determined from the Langevin-Bikerman (LB) equation with an excluded volume derived for a monovalent salt electrolyte solution in contact with a charged surface:^2,4

$\begin{array}{l}{\nabla }^2\phi (\mathbf{r})=\frac{2e_0{n}_0{n}_s}{{\varepsilon }_0}\frac{\text{sinh}(e_0\phi \beta )}{H(\phi ,E)}\\ -\frac{n_{0w}{n}_s{p}_0}{{\varepsilon }_0}\nabla ·\left[\mathbf{n}\frac{F(p_{0}E\beta )}{H(\phi ,E)}\right],\end{array}$(B.1)

where

$F(p_{0}E\beta )=L(p_{0}E\beta )\frac{\text{sinh}(p_{0}E\beta )}{p_{0}E\beta },$(B.2)

$L(p_{0}E\beta )=[\text{coth}(p_{0}E\beta )-1/(p_{0}E\beta )],$(B.3)

$H(\phi ,E)=2n_0\hspace{0.17em}\text{cosh}(e_0\phi \beta )+\frac{n_{0w}}{p_{0}E\beta }\text{sinh}(p_{0}E\beta ).$(B.4)

Here e₀ is the elementary charge, p₀ is the dipole moment of water (or a small cluster of water molecules), ɛ₀ is the permittivity of free space, ϕ is the electric potential, E = /Δφ/ is the magnitude of electric field strength, n is the unit normal vector in the direction of Δφ, β= 1/kT, kT is the thermal energy and n_0w = n_s –2n₀ is the number densities of water molecules in the bulk, n_s is the number density of lattice sites² and n₀ the bulk number density of monovalent salt anions and cations. The above differential equation has two boundary conditions. The first states that the electric field is zero far away from the charged surface:

$\nabla \phi (\text{r}\to \infty )=0.$(B.5)

The second boundary condition at the charged surface demands the electro-neutrality of the whole system and is obtained by integrating Eq. (B.1)$\begin{array}{l}{\nabla }^2\phi (\mathbf{r})=\frac{2e_0{n}_0{n}_s}{{\varepsilon }_0}\frac{\text{sinh}(e_0\phi \beta )}{H(\phi ,E)}\\ -\frac{n_{0w}{n}_s{p}_0}{{\varepsilon }_0}\nabla ·\left[\mathbf{n}\frac{F(p_{0}E\beta )}{H(\phi ,E)}\right],\end{array}$(B.1) (see):^2,3

$\nabla \phi {\mid }_{\mathbf{r}={\mathbf{r}}_{\text{surf}}}=-\frac{\sigma }{{\varepsilon }_0}\mathbf{n}-\mathbf{n}\frac{n_{0w}{n}_s{p}_0}{{\varepsilon }_0}\frac{F(p_{0}E\beta )}{H(\phi ,E)}{\mid }_{\mathbf{r}={\mathbf{r}}_{\text{surf}}},$(B.6)

where σ is the surface charge density. The above LB Eq. (B.1)$\begin{array}{l}{\nabla }^2\phi (\mathbf{r})=\frac{2e_0{n}_0{n}_s}{{\varepsilon }_0}\frac{\text{sinh}(e_0\phi \beta )}{H(\phi ,E)}\\ -\frac{n_{0w}{n}_s{p}_0}{{\varepsilon }_0}\nabla ·\left[\mathbf{n}\frac{F(p_{0}E\beta )}{H(\phi ,E)}\right],\end{array}$(B.1) for finite sized ions can be rewritten in the form:⁴

$\nabla ·[{\varepsilon }_0{\varepsilon }_r(\mathbf{r})\nabla \phi (\text{r})]=-{\rho }_{free}(\mathbf{r}),$(B.7)

where ρ _free (r) is the macroscopic (net) volume charge density of co-ions and counter-ions:⁴

${\rho }_{free}(\mathbf{r})=-2e_0\hspace{0.17em}{n}_s{n}_0\frac{\text{sinh}(e_0\phi \beta )}{H(\phi ,E)},$(B.8)

and ɛ_r is the relative permittivity of the electrolyte solution in contact with the charged surface:⁴¹

${\varepsilon }_r(\mathbf{r})=1+n_{0w}{n}_s\frac{p_o}{{\varepsilon }_o}\frac{F(p_{0}E\beta )}{EH(\phi ,E)}.$(B.9)

In the above Eq. (B.9)${\varepsilon }_r(\mathbf{r})=1+n_{0w}{n}_s\frac{p_o}{{\varepsilon }_o}\frac{F(p_{0}E\beta )}{EH(\phi ,E)}.$(B.9) we assume n₀ << n_s and therefore n_s ≈ n_0w. The cavity and reaction fields are not taken into account.²⁴

The second boundary condition (Eq. (B.6)$\nabla \phi {\mid }_{\mathbf{r}={\mathbf{r}}_{\text{surf}}}=-\frac{\sigma }{{\varepsilon }_0}\mathbf{n}-\mathbf{n}\frac{n_{0w}{n}_s{p}_0}{{\varepsilon }_0}\frac{F(p_{0}E\beta )}{H(\phi ,E)}{\mid }_{\mathbf{r}={\mathbf{r}}_{\text{surf}}},$(B.6) ) can be rewritten as:⁴

$\nabla \phi (\mathbf{r}={\mathbf{r}}_{surf})=-\frac{\sigma \mathbf{n}}{{\varepsilon }_0{\varepsilon }_{\text{r}}(\mathbf{r}={\mathbf{r}}_{surf})},$(B.10)

where ɛ_r (r) is defined by Eq. (B.9)${\varepsilon }_r(\mathbf{r})=1+n_{0w}{n}_s\frac{p_o}{{\varepsilon }_o}\frac{F(p_{0}E\beta )}{EH(\phi ,E)}.$(B.9) . The above expression for ɛ_r (Eq. (B.9)${\varepsilon }_r(\mathbf{r})=1+n_{0w}{n}_s\frac{p_o}{{\varepsilon }_o}\frac{F(p_{0}E\beta )}{EH(\phi ,E)}.$(B.9) ) is consistent with the definition of the relative permittivity in the form ɛ_r = 1 + |P|/ɛ ₀E,^2,3 where P is the polarization vector.

In this work Eq. (B.7)$\nabla ·[{\varepsilon }_0{\varepsilon }_r(\mathbf{r})\nabla \phi (\text{r})]=-{\rho }_{free}(\mathbf{r}),$(B.7) was solved numerically using the Finite Element Method (FEM) within the Comsol Multiphysics 3.5a Software program package (Stockholm, Sweden). The space dependence of ɛ_r (r) (Eq. (B.9)${\varepsilon }_r(\mathbf{r})=1+n_{0w}{n}_s\frac{p_o}{{\varepsilon }_o}\frac{F(p_{0}E\beta )}{EH(\phi ,E)}.$(B.9) ) in Eq. (B.7)$\nabla ·[{\varepsilon }_0{\varepsilon }_r(\mathbf{r})\nabla \phi (\text{r})]=-{\rho }_{free}(\mathbf{r}),$(B.7) is taken into account in an iterative procedure where the initial value of ɛ_r (r) is a constant equal to the permittivity of the bulk solution.

Figure B.2 shows a substantial decrease of ɛ_r in the vicinity of a charged planar surface. The predicted decrease of the permittivity relative to its bulk value is the consequence of the orientational ordering of water dipoles in the vicinity of the charged surface and the depletion of water dipoles at the charged surface due to accumulation of counterions, as shown schematically in Figure B.1. The profound decrease of ɛ_r near the charged surface at higher values of the surface charge density/σ/(Figure B.2) according to Eq. (B.10)$\nabla \phi (\mathbf{r}={\mathbf{r}}_{surf})=-\frac{\sigma \mathbf{n}}{{\varepsilon }_0{\varepsilon }_{\text{r}}(\mathbf{r}={\mathbf{r}}_{surf})},$(B.10) strongly increases the electric field strength at the charged surface E = – Δϕ(r = r_surf) and therefore also the attraction of osteoblasts to the negatively charged metal surface.

Figure B.2 Effective relative permittivity ɛ_r as a function of the distance from the planar charged surface x calculated within the presented Langevin PB theory with excluded volume for three values of the surface charge density: σ = − 0.1 As/m² (dotted line), −0.2 As/m² (dashed line) and −0.4 As/m² (full line). Eqs.(B.7)$\nabla ·[{\varepsilon }_0{\varepsilon }_r(\mathbf{r})\nabla \phi (\text{r})]=-{\rho }_{free}(\mathbf{r}),$(B.7) –(B.10)$\nabla \phi (\mathbf{r}={\mathbf{r}}_{surf})=-\frac{\sigma \mathbf{n}}{{\varepsilon }_0{\varepsilon }_{\text{r}}(\mathbf{r}={\mathbf{r}}_{surf})},$(B.10) were solved numerically for planar geometry using the Finite Element Method as described in the text. The dipole moment of water p₀ was taken as 4.794 D, the bulk concentration of salt n₀/N_A = 0.15 mol/L and the bulk concentration of water n_0w/N_A = 55 mol/L.