Intracellular hyperthermia: Nanobubbles and their biomedical applications

Abstract

Functionalised nanoparticles have been proposed as potential agents for non-invasive therapies where an external source such as a laser or an electro-magnetic wave is used to heat targeted particles for either drug release or malignant cell damage. It is desirable to have intracellular reactions to minimise the damage to health cells. However, it is still debatable from the thermal response point of view, whether intracellular hyperthermia is better than extracellular delivery due to conventional ideas of localisation of heat by nanoparticles. This work conducts an analytical study on the heating of a single nanoparticle by a pulsed laser and reveals the potential role of the formation of nanobubbles around heated particles. The rapid formation and contraction of bubbles around heated nanoparticles, associated with the propagation of pressure waves, could bring thermal-mechanical damage to surrounding cells at a dimension much larger than that of a nanoparticle. The challenges of the study of nanobubbles are highlighted and their potential healthcare implications are discussed.

• hyperthermia
• nanoparticles
• laser
• vapour bubble
• explosive boiling
• cancer therapy

Introduction

Nanoscale thermal response is crucial for a number of biomedical applications such as endogenous and exogenous absorbers for optothermal imaging and targeted photothermal medical therapies for controlled drug delivery and selective tissue damage at the cellular level [1–3]. Functionalized magnetic nanomaterials such as Fe₂O₃, Fe₃O₄ and Ni have been proposed as potential agencies for non-invasive therapies [1],[4]. Very recently, carbon-coated cobalt nanoparticles, gold nanoparticles (GNPs) and carbon nanotubes have been investigated for non-invasive radiofrequency ablation (RFA) and the feasibility has been confirmed in preliminary studies on non-targeted particles in vitro, and later in vivo [3],[5],[6]. The process involves delivering bio-modified nanoparticles to malignant cells and heating nanoparticles with external electromagnetic radiation. The subsequent rapid temperature increase results in the cell destruction.

An understanding of the heating of nanoparticles in situ is essential for these different healthcare applications. It is expected that an intracellular delivery will be much more beneficial due to the minimum damage to health cells. However, there are many debates on the killing mechanism of nanoparticle-mediated cancer therapies. From the thermal response point of view, it is still unclear whether an intracellular delivery is better than an extracellular delivery due to conventional ideas of localization of heat by nanoparticles, typified by Rabin [7] and Keblinski et al. [8]. Both studies are based on a similar approach analysing diffusive heat flow equations based on quasi-stationary and quasi-equilibrium considerations. For magnetic nanoparticles heated by external electromagnetic waves or gold nanoparticles heated by continuous wave lasers, both studies reach similar conclusions that the heating of individual nanoparticles is negligible and the temperature increase is localised to a small regime around nanoparticles. The rise of temperature in surrounding liquid by a single nanoparticle is too small to be significant in malignant cell killing. The effectiveness of intracellular therapy is questioned from the thermal response point of view.

In many of these applications, nanoparticles are heated in a transparent surrounding by pulsed lasers. With the advancement of laser technologies, more powerful and faster lasers, from a few nanoseconds to a few femtoseconds, are being increasingly used. This will bring rapid heating of nanoparticles that can induce high temperatures spatially confined to the particles. A simple estimation based on typical Photothermal Therapy (PPT) experiments [2],[9] shows that gold nanoparticles can be easily heated to 1000°C in a few nanoseconds, or more under strong electromagnetic fields. It is believed that such transient heat could cause physical damage to adjacent cells by a variety of possible mechanisms such as protein denaturation, melting of hot nanoparticles into cell walls and a rapid vapour bubble formation around nanoparticles, where little information is available. It is expected that this transient vapour bubble formation could induce highly localised thermo-mechanical damage to biological structures that is dependent upon bubble dynamics such as bubble velocity and size.

This work will investigate the heating of a single nanoparticle in an aqueous solution under different pulsed laser conditions. More importantly, it will examine possible bubble formation around nanoparticles and reveal its potential role in nanoparticle mediated therapies and future biomedical applications.

Theoretical considerations

Time scale

For many ultrafast laser applications, the time scale of laser pulses is comparable to that of energy carriers such as electrons and phonons. Table I summarises various processes associated with ultrafast laser heating of metallic nanoparticles. The heating of a nanoparticle and the subsequent heat dissipation from the nanoparticle to the surroundings occur in a cascade of events [10],[11]. When the particle is exposed to an ultrafast laser pulse, free electrons absorb the energy of photons and increase their kinetic energy. These highly energetic electrons, having a non-equilibrium distribution of energy, are relaxed through electron-electron scattering in the order of 10 ∼ 50 femtoseconds. Practically, there is little energy exchange between electrons and phonons within this time scale, and electrons stay in a high energy level. The lattice temperature starts increasing as a result of electron-phonon scattering. A thermal equilibrium between the electrons and the lattice is reached at a time scale of tens of picoseconds depending on the initial rise of electron energy. As the particle temperature increases, energy exchange between the particle and its surrounding medium begins to take place through the phonon-phonon coupling, which dissipates heat across the particle-medium interface to an adjacent liquid shell at a rate dependent on the interfacial resistance and thermophysical properties of the solid and liquid medium. The temperature difference between the particle and liquid medium diminishes as a thermal equilibrium is achieved, typically within a few hundred picoseconds to ∼1 nanosecond depending on the liquid medium, particle size and laser pulse intensity.

Table I.  The time-scale of different processes for ultrafast heating.

Diffusion model

The characteristic time, t₀, required for the development of a quasi-stationary temperature profile inside the particle can be estimated from the diffusion formula: where r_p and are the radius and the thermal diffusivity of the solid particle. For gold nanoparticles, ∼ 1.2 × 10⁻⁴ m²/s, the characteristic time for a quasi-stationary temperature profile is ∼2 ps for a particle size of 10 nm. In many experimental cases, t₀ is much smaller than the characteristic times of laser pulse durations and the heating of a particle. For most of metallic nanoparticle applications, its small size and high thermal conductivity ensure that the temperature difference inside the particle is small. As a consequence, the heating of a nanoparticle can be represented by one uniform particle temperature, T_p, as belowwhere the subscript _p refers to the particle, t is the time, T is the temperature, , c, V and S are the density, specific heat capacity, volume and surface area of the particle, I(t) is the irradiation density, K_ab is the absorption coefficient and j is the energy flux density removed from the particle surface that has a contribution of conduction, j_c, evaporation, j_e, and radiation, j_r.

Under the condition of t > t_T, where is the thermal dissipation time constant, the quasi-stationary temperature distribution around the particle in a spherical coordinate system with the origin at the particle centre was obtained by assuming a temperature-dependent media thermal conductivity, k, in the form of , where and are the temperature and the thermal conductivity of liquid at an infinite location and a is a constant [12].

A strong temperature gradient in the surrounding media is followed from Equation 3. The differentiation of Equation 3 at the interface gives heat transfer across the interface and substantial heat loss from the particle into the surrounding medium can occur.

At a relatively low temperature, i.e. lower than the melting temperature of solid particles, the contribution of metal evaporation and radiation is small. An analytical solution can be found for Equation 1 for a heating pulse, assuming a constant irradiation density I and a constant thermal conductivity for the surrounding medium [13].where r_p is the radius of the particle and B is defined as

For the condition of Bt_p ≪ 1, i.e t_p ≪ t_T, the loss of heat from the particle by heat conduction during the heating time t_p can be neglected, the expansion of the exponential function gives the maximal temperature of the particle at the end of the heating time (t = t_p), T_max

The cooling of the particle after the heating pulse can be written aswhere c is defined as .

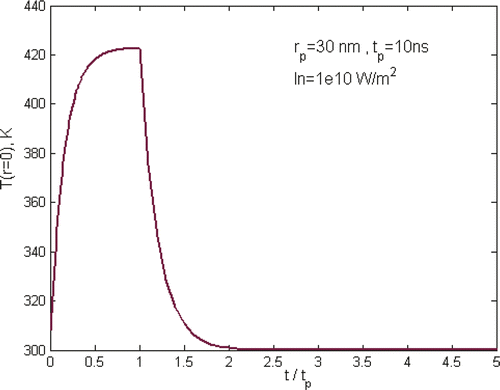
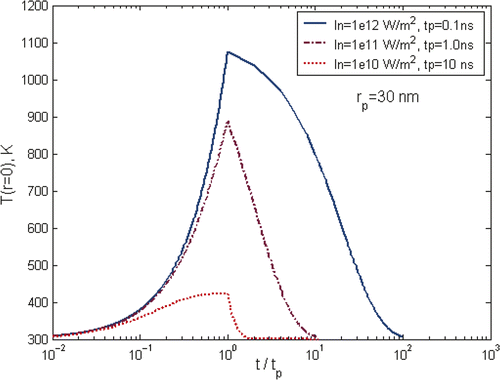
Figure 1 shows a typical temperature curve during the heating and cooling of a laser pulse of 10 ns where In is defined as In = IK_ab, and Figure 2 gives an overview of gold nanoparticle temperature profile under different laser pulses, but keeping the total energy input per pulse the same. It shows clearly that the maximum temperature of particles is strongly dependent on the selection of laser parameters. The characteristic time for heat exchange between a single spherical particle and surrounding medium and the formation of a quasi-stationary distribution of temperature in the medium around the particle is decided by the thermal relaxation time , where is the coefficient of thermal diffusivity of the medium. For gold nanoparticles of 30 nm in aqueous solution as in the simulation, the thermal relaxation time is ∼1.3 ns. For long laser pulses, i.e. pulse duration, t_p is much longer than the thermal relaxation time t_T, t_p ≫ t_T, as in the case shown in Figure 1, it will cause heating of both the particle and the surrounding media as heat diffuses across the particle boundary. As a consequence, the nanoparticle temperature rises rapidly at the beginning of the pulse, i.e. t < 0.6t_p, and slows down significantly in the later heating period. It approaches asymptotically to a plateau until the end of the heating pulse. For short laser pulse, i.e. t_p ≪ t_T as the case of t_p = 0.1 ns in Figure 2, there is practically no heat exchange between the particle and its surroundings during the pulse period. As a consequence, the laser energy is thermally confined within the particle, causing a rapid heating of the particle itself and reaching ∼1100 K at the end of the laser pulse. For the case of t_p ∼ t_T as illustrated by the case of t_p = 1 ns in Figure 2, the heating and cooling behaviour is in the transition zone where the energy transfer is bounded between the regime of thermal confinement to the regime of heat diffusion from the particle.

Figure 1. Typical heating and cooling curve of a gold nanoparticle in H₂O (t_p ≪ t_T).

Figure 2. The effect of laser pulses on the temperature of gold nanoparticles surrounded by water.

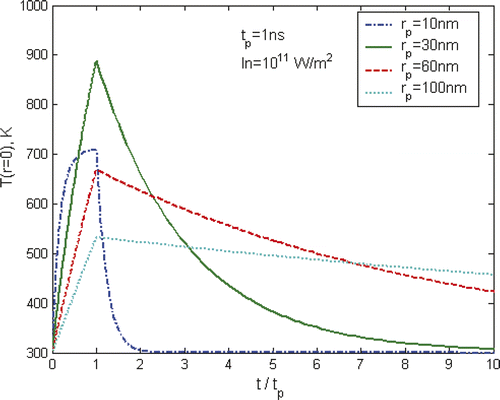
Apart from a strong dependence on laser pulses as shown in Figure 2, the heating and cooling of nanoparticles are also affected significantly by the particle size. Figure 3 illustrates such a trend using a laser pulse of t_p = 1 ns and In = 10¹¹ W/m² as an example. The maximum temperature of gold nanoparticles increases significantly from 10 to 30 nm, but decreases as the particle size increases further. The variation of particle size will change significantly the thermal relaxation time of the particle due to the strong square dependence of the particle size, i.e. . The increase in particle size will increase the heat capacity of the particle which has a trend of reducing the temperature increase; however, in the mean time it will increase the relaxation time that will reduce the amount of heat dissipation from the particle to surrounding liquid that may result in an increase of the particle temperature. It is apparent that there is an optimized particle size to achieve the maximum heating effect.

Figure 3. Influence of particle size on the transient temperature profile of gold nanoparticles.

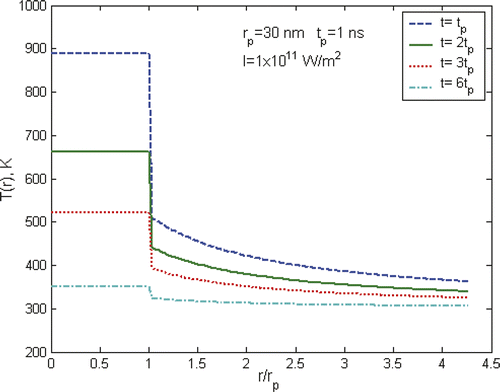
Figure 4 shows the radial temperature profile of gold particles and water at different times. It is apparent that there are rapid temperature drops across the interface of solid particles and the liquid medium. At a distance of only a nanoparticle radius away from the interface, the temperature drops to a typical value of about 50% of the temperature at the particle surface. Further away to a distance of a few times of the nanoparticle radius, the temperature is close to the surrounding bulk temperature. From these results, it appears that the heating effect of a nanoparticle is confined to a very small area around the nanoparticle in a very short period, i.e. a few nm in radius and a few ns in duration, which appears to be not enough to cause any significant damage to surrounding cells, even under high power laser situations. As such, it was concluded that the effectiveness of the heating of nanoparticles is negligible and the intracellular therapy is not an advantage compared to extracellular therapy [7]. However, we will show in the next section that the generation of nanobubbles will change such a view. Of particular note is that at the interface of the nanoparticle and surrounding liquid only a conduction boundary condition is applied, i.e. a constant heat flux condition, in above calculations. The significance of the interfacial resistance was not considered in the analysis. The existence of the interfacial resistance will increase the temperature drop across the interface that is strongly dependent on the wetting capability between the liquid and solid particle. Interested readers may find further information from Huxtable et al. [14] and Hu et al. [15].

Figure 4. Transient radial temperature profile of one gold nanoparticle in water.

Implication of above calculations (formation of bubbles and pressure waves)

It has to be remembered that previous calculations are based on pure liquid conduction with constant thermophysical properties and no phase change occurrences. Nevertheless, in practical situations, the pulsed heating of a nanoparticle can easily produce a particle temperature over the critical temperature of the surrounding liquid, which will cause strong vaporisation of water near the particle surface and a vapour blanket (bubble) can be formed around the particle. The generation and rapid initial expansion of these bubbles would generate a pressure wave that would propagate into the tissue, which might bring a large detrimental effect to surrounding cells. The bubble dynamics such as bubble expansion/contraction speed, bubble size and frequency will determine the damage range in the tissue. For nanoparticle-mediated heating of cancer therapies, the formation of vapour bubbles may also insulate the particle from laser radiation and surrounding liquid as soon as the bubble is formed. The direct contact of particle with the vapour having much reduced thermal conductivity will also change significantly the heat transfer process.

Analysis of nanobubbles

The origination of vapour bubbles could be homogeneous or heterogeneous in nature. Bubble formation in liquids devoid of any impurities is termed homogeneous bubble nucleation in contrast to heterogeneous bubble nucleation. Due to the small nanoparticle size, it might be sufficient to consider a nanoparticle suspension as a homogeneous nucleation mode. When a liquid is heated very rapidly, a metastable state can be reached in which the liquid begins to boil at a temperature much higher than its usual equilibrium boiling point. The evaporation process can be of an explosive nature.

The detailed modelling of bubble dynamics is very difficult. The behaviour of the nanoparticle–vapour–water system can be described by a system of equations including heat conduction equations for nanoparticles vapour and liquid, equation for homobaricity approximation for vapour pressure, equations for bubble mass and bubble dynamic, with initial and boundary conditions, and continuity and incompressibility equations for surrounding liquid. Different from conventional bubble phenomena, laser-induced bubbles are small due to the large subcooling effect in the cell environment, i.e. typically at µm or nm size, and highly transient, i.e. with a life-time of less than a few µs. It could be accompanied by strong pressure wave transportation. A systematic investigation of these phenomena is currently lacking. For the rapid expansion process of vapour bubbles, it can be assumed to be inertia-limited. As a very rough estimation, the Rayleigh equation will be used in the modelling of bubble dynamics, which is shown belowwhere t_b is the bubble growth time, C is an empirical constant, C = 0.915, is the liquid density, p_s(T ) and p_s() are the saturation pressure of vapour at temperature T and , and is the maximum bubble diameter that can be estimated from the energy conservation principle.where E is the total energy absorbed by the particle for the bubble growth, , where is the percentage of energy used for the formation of bubble and thermal energy increase of the particle at this time instant. The bubble velocity can be estimated as

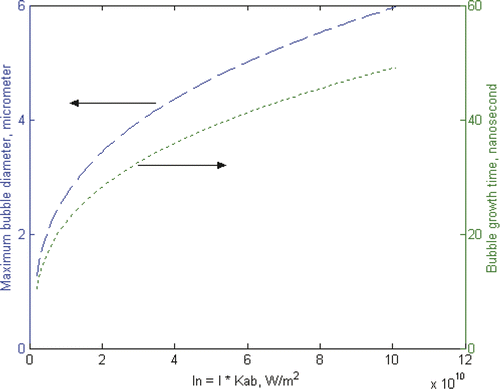
Figure 5 illustrates the possible maximum bubble diameter and bubble growth time as a function of laser irradiation power. In the calculation, the laser pulse length is fixed at 10 ns, which is the typical laser pulse used in conventional biomedical applications. As homogeneous nucleation temperature is generally considered to be 80% ∼ 90% of the critical temperature [16], a quasi-homogeneous nucleation is assumed in the calculation and the nucleation temperature is taken as 600 K when a 1-nm thick vapour film is generated instantly around the gold nanoparticle. is decided by calculating the energy required to bring the gold nanoparticle and surrounding water of 2-nm thickness to the nucleation temperature and the latent heat for initial bubble generation. Such a simple calculation illustrates some typical characteristics of bubbles around nanoparticles. Under such conditions, the generation of bubbles has an explosive nature. Within a very short period of ∼10 nanoseconds, bubbles of ∼1 µm in diameter are generated and reach their maximum diameter of a few µm in less than 1 µs.

Figure 5. Estimation of bubble parameters based on the Rayleigh equation (t_p = 10 ns, r_p = 30 nm).

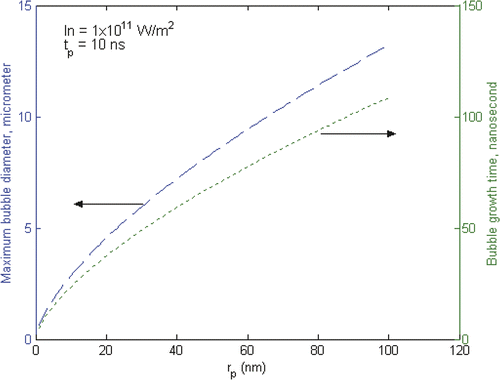
Figure 6 shows the effect of particle size on the bubble formation using a fixed laser pulse of 10 nm and intensity of IK_ab = 1 × 10¹¹ W/m². It shows that the maximum bubble diameter and growth time increase with increasing particle diameters. The maximum bubble diameter is a few hundred times larger than the particle size.

Figure 6. Influence of particle size on bubble parameters.

Different from the pure diffusion calculation as in Figure 4, these results clearly show that the influence of a single nanoparticle can reach a distance of a few µm, which is much larger than the size of particle itself. It is also larger or comparable to typical cells. As a consequence, the generation of vapour bubbles around nanoparticles causes a non-linear flow of heat and breaks the conventional geometry limitation of pure heat diffusion. Furthermore, the very high bubble velocity during the bubble expansion stage, which is estimated as ∼90 m/s for this case, will induce a strong acoustic pressure wave considering the non-compressible nature of the surrounding liquid. With the rapid expansion of vapour bubbles, strong condensation will also occur at the vapour-liquid interface due to the large subcooling effect. At the initial stage when the evaporation rate is exceeding the condensation rate, the bubble grows. At the later stage when the condensation rate becomes larger than the evaporation rate, a rapid contraction of bubbles may occur. It has been estimated that the bubble contraction speed is also in the order of ∼10 m/s. Depending on the laser repetition rate and bubble dynamics, there is a possibility that under certain conditions, the vapour bubble will expand and contract periodically rather than a full bubble collapse. Such an oscillation would induce a periodic pressure wave that would reach deep into the tissue, causing long-distance mechanical damage. As a consequence, these combined effects break the limitation of localisation of heat by nanoparticles, and cause thermal-mechanical damage in a dimension that is much larger than that of a single nanoparticle. From a thermal response point of view, such a long distance influence induced by a single nanoparticle is independent of the location of particles. Intracellular hyperthermia therefore could achieve a similar thermal effect as that of extracellular hyperthermia.

Nanobubbles and their potential biomedical applications

Recent experimental evidence of nanobubbles

Recently there has been some experimental evidence showing the physical existence of nanobubbles or microbubbles around small particles [16–18]. For instance, by applying an X-ray scattering to a femtosecond laser-excited particle solution, Kotaidis and Plech and Kotaidis et al. [16],[19] found that gold particles of 9 ∼ 110 nm in diameter could be excited by a nanosecond laser to produce large vapour bubbles that grow and decay within 1 ns. The generation of vapour bubbles insulates the particle from the surrounding media that resulted in a rapid increase of particle temperature. Depending on the laser pulse and nanoparticle diameters, the observed vapour bubble volume could be ∼100 times larger than the particle volume, which is smaller than the estimation from the Rayleigh equation, Figure 5. Possible reasons for this inconsistency may include large input laser energy loss in the experiments, the simplification of bubble model by the Rayleigh equation and an increased heat input for bubble growth by neglecting the interfacial resistance, as well as different laser parameters being used. A detailed modelling requires further study.

Based on a time-solved microscopy method, Neumann and Brinkmann [18],[20] investigated the bubble dynamics of a micro-sized particle heated by 12 ns laser pulses. Depending on the laser pulse intensity, the bubble growth velocity was found to vary from 10 to 100 m/s, which suggests that the bubble expansion took place in strongly superheated water around the particle and bubble formation had an explosive nature. Such an explosion character is believed to be able to generate a strong pressure wave that has a much longer impact distance than the particle and vapour bubble size. For instance, for shot pulses of intensive radiation, the particle and surrounding tissue heating can occur at an extremely high rate, i.e. 10¹⁰ ∼ 10¹⁴ K/s is achievable. As vapour forms around the particle, assuming an initial saturated status, the pressure inside the vapour is around ∼100 bar at a sub-critical temperature of ∼600 K, which will induce an intensive pressure wave that results in mechanical damage or rupture of surrounding cells. Such a mechanism is speculated as the one of the major killing mechanisms for laser-induced nanoparticle therapy.

Further detailed studies on bubble dynamics, the associated pressure wave propagation and the interaction with surrounding cell tissues are apparently needed in order to enhance our understanding on the nanoscale bubble phenomena and employ it as an effective tool for biomedical applications. Two examples are given below to illustrate some potential applications of nanobubbles.

Radio-frequency or laser ablation of cancer cells

For biomedical applications, heat can be produced by microwave, magnetic induction heating, ultrasound sources and more recently, by light through the plasmon resonance effect, the so-called photothermal therapy (PTT). Biomolecular tagged gold nanoparticles (GNPs), which have absorption resonance at ∼520 nm, have been used in PTT due to their enhanced absorption rate, which are four to five orders of magnitude larger than that of conventional photoabsorbing dyes. This strong absorption ensures effective laser therapy at relatively lower energies rendering the therapy method minimally invasive. Engineering gold nanoparticles into shell-core structure or nanorods with large aspect ratios can push the resonance wavelength into the near-infrared (NIR) regime. However, PTT is still limited to superficial tumours due to the limited penetration depth of visible or NIR light.

Different from laser heating of gold nanoparticles, certain frequency bands of RF are transparent to the human body that could be used to treat deep-seated tumours. Conventional RF heating employs a current passing through tissue from an active electrode leading to ion agitation, which is converted by means of friction into heat. Using gold nanoparticles as heat receptors can make heating more rapid, uniform or selective depending on the distribution of gold nanoparticles. Very recently, the possibility of using radiofrequency radiation (RF) for gold nanoparticle mediated hyperthermia or ablation has been proposed and the feasibility has been confirmed in preliminary studies on non-targeted particles in vitro, and later in vivo [5],[6],[21]. In these experiments, a RF frequency of 13.56 MHz and very low concentrations of gold nanoparticles, in the order of , were used. No salient heating effect should be expected under such conditions. However, significant treatment effect was obtained.

Unlike the phasmon resonance process and RF heating of magnetic nanoparticles that has been intensively investigated [2],[4],[9], the mechanisms of RF heating on gold nanoparticles is still not clear. It is known that the temperature rise is related to the particle size, surrounding medium and the frequency and the duration of the external RF field. However, it still remains unclear why low concentration of GNPs can significantly enhance RF-induced heating of malignant cells. It is speculated that a certain frequency RF will interact with gold nanoparticles strongly to increase their temperature rapidly. The interfacial resistance, namely the Kapitza resistance, will affect how heat is transferred from high temperature GNPs to surrounding cells. More importantly, as demonstrated above, bubbles can be easily generated on particle surfaces, which could induce a propagating pressure wave to cause thermal-mechanical damage to surrounding cells. Understanding these processes, especially the interactions of RF and gold nanoparticles and subsequent bubble dynamics, will have a great impact on RF therapy. More complicated cases will arise for applications in vivo as the presence of blood flow and tissue microenvironment will significantly affect the heat transfer and bubble dynamics, which requires further studies.

‘Nano-bomb’ induced by more powerful lasers

Some researchers have considered a more radical way of selective laser killing of abnormal cells by laser thermal explosion of single nanoparticles (nano-bombs) delivered to the cell [22],[23]. Thermal explosion is realized when heat is generated within a strongly absorbing particle more rapidly than the heat can diffuse away (similar to fusion by laser method). Based on some energy balance estimations, it was shown that the threshold energy density of a single laser pulse required for the thermal explosion of a solid gold nanosphere is achievable by using high-power picosecond lasers. The threshold value can be reduced further by using large nanorods or structured nanoparticles whose optical plasomon resonance lies in the near infrared region. The therapeutic effect is achieved through nonlinear phenomena that accompany the thermal explosion of nanoparticles, including the generation of GNP explosion products with high kinetic energy (fragmentation process) and strong shock waves with supersonic expansion in the cell volume or producing optical plasma.

Conclusions

Aiming to enhance our understanding on the intracellular hyperthermia, this work conducted an analytical study of the heating of a nanoparticle in an aqueous solution under pulsed laser conditions. The major findings can be concluded as:

1. High temperature increase of a single nanoparticle can be achieved by using suitable pulsed lasers. The heating effect is dependent on particle size, thermophysical properties and laser pulse selection. There is an optimal nanoparticle size and laser pulse to achieve the maximum heating effect.

2. Under optimum conditions, bubbles can form around heated nanoparticles, which challenge the conventional thought of localisation of heat by nanoparticles for intracellular hyperthermia.

3. The formation of nanobubbles has an explosive nature, which can reach a few µm in tens of ns, dependent on the heating effect. The rapid formation and contraction of bubbles around heated nanoparticles, associated with the propagation of pressure waves, could bring thermal-mechanical damage to surrounding cells at a dimension much larger than that of a nanoparticle. Intracellular hyperthermia could achieve a similar thermal effect as that of extracellular hyperthermia.

4. Examples of potential applications show that nanobubbles around heated nanoparticles could be used for future cancer therapy.

Future work on detailed modelling of nanobubbles is currently ongoing.

Acknowledgement

The author would like to extend his thanks to EPSRC for financial support under Grant EP/E065449/1.

Declaration of interest: The author reports no conflicts of interest. The author alone is responsible for the content and writing of the paper.