Simulation studies promote technological development of radiofrequency phased array hyperthermia

Abstract

A treatment planning program package for radiofrequency hyperthermia has been developed. It consists of software modules for processing three-dimensional computerized tomography (CT) data sets, manual segmentation, generation of tetrahedral grids, numerical calculation and optimisation of three-dimensional Ε field distributions using a volume surface integral equation algorithm as well as temperature distributions using an adaptive multilevel finite-elements code, and graphical tools for simultaneous representation of CT data and simulation results. Heat treatments are limited by hot spots in healthy tissues caused by Ε field maxima at electrical interfaces (bone/muscle). In order to reduce or avoid hot spots suitable objective functions are derived from power deposition patterns and temperature distributions, and are utilised to optimise antenna parameters (phases, amplitudes). The simulation and optimisation tools have been applied to estimate the improvements that could be reached by upgrades of the clinically used SIGMA-60 applicator (consisting of a single ring of four antenna pairs). The investigated upgrades are increased number of antennas and channels (triple-ring of 3 × 8 antennas and variation of antenna inclination. Significant improvement of index temperatures (1–2°C) is achieved by upgrading the single ring to a triple ring with free phase selection for every antenna or antenna pair. Antenna amplitudes and inclinations proved as less important parameters.

• radiofrequency hyperthermia
• hyperthermia treatment planning
• annular-phased-array applicator

Introduction

Radiofrequency hyperthermia using annular phased array applicators is used in the treatment of pelvic tumours [1], [2], particularly soft tissue sarcomas [3], [4] and rectal carcinomas [5], [6]. The most popular system is the BSD-2000 with SIGMA applicators (BSD Medical Systems Corp.). Analyses of clinical temperature data have already indicated that the controllability of relative power distributions is limited for this applicator type [7]. In fact, the temperature in the tumour is influenced predominantly by an increase in total power. Clinically, total power is limited by localised discomfort experienced by the patient which often occurs at characteristically predisposed sites (so-called hot spot phenomena). These hot spots are related to local maxima in the electric field that occur at electrical interfaces perpendicular to the direction of the field and are fundamentally due to the three-dimensional nature of the human body [8].

Two-dimensional model calculations performed by Strohbehn et al. [9] and Wust et al. [10] awoke hopes that adjusting the phase and amplitude in the ring applicator would allow the user to control the power distribution. This expectation was not confirmed in clinical practice. Three-dimensional model calculations reveal why—the formation of hot spots cannot be predicted in the two-dimensional model calculation, because it assumes that the electrical field is always at a tangent to the interfaces. In addition, the existing practical approaches for improving control using visualising phantoms [11] and phase-sensitive electric field sensors [12] have been developed for a two-dimensional set-up, as have the applicators themselves. The TEM applicator developed by De Leeuw and Lagendijk [13] and the 4-wave guide applicator developed by van Dijk et al. [14] are also annular phased array (ΑΡΑ) applicators. All ΑΡΑ applicators are similar in the degree of two-dimensional control of power distribution offered [15]. There is a degree of three-dimensional control of power distribution (in the z-direction corresponding to the longitudinal axis of the patient) when using the TEM applicator (refer for example to De Leeuw et al. [16]).

An improved applicator design should first be tested using simulation studies with a suitable hyperthermia planning system, as carried out by Wust et al. [8]. Choosing the ‘correct’ 3D patient model and numerical method for the 3D calculation of the electric field is by no means a simple task, and is the subject of research. We consider an essential test of a planning system to give the qualitatively correct prediction of clinical observations, for example the existence and localisation of hot spots or the estimation of the degree of difficulty of a heat treatment in dependency on tumour localisation.

We have used two program systems for patient-specific model calculation. The Stanford planning system [17] is based on the finite difference time domain (FDTD) method which starts with a discretization of the problem domain by a regular grid consisting of cubes (voxel model). When using this method, difficulties occur if the electrical interfaces do not fit to the cubic grid. In this case sharp discontinuities of the Ε-field and in consequence the SAR distribution are not adequately modeled [8]. In contrast, the planning system developed in Berlin is based on a volume surface integral equation (VSIE) method [18], [19] and a discretization by tetrahedral grids which are produced using an interactively designed contour model [20], [21]. The electric field distributions calculated using the VSIE method are greatly influenced by the geometry of electrical interfaces and are consequently considerably different to the results from the FDTD method (based on the voxel model). If the FDTD method is employed using the same contour model, the results from the two methods become more similar, particularly after correction of the FDTD results by a special postprocessing procedure based on the contours [22]. Our clinical experience with regional hyperthermia is best described using the VSIE method. We therefore believe that the VSIE method is suitable for simulation studies on realistic three-dimensional patient models.

The following simulation study is based on a SIGMA 60 applicator, and examines the potential temperature distributions that could be reached by upgrading the system, in accordance to [23]. The modifications made promise better control in the z-direction: increasing the number of antennas and arranging them three-dimensionally, increasing the number of independently controllable channels, and varying the spatial orientation of the antennas. Optimisation calculations are performed for each stage of upgrading, studying a large number of descriptors derived from the SAR and temperature distributions. The optimised distributions are compared in order to assess the gain from each upgrade. We use rectal carcinomas at different locations as tumour models.

Methods

Two standard tumour models from clinical practice were chosen for the theoretical evaluation of radiofrequency hyperthermia treatment. Patient 1 had a cranially located presacral recurrence of a rectal carcinoma with destruction of the sacrum (following abdominoperineal rectal extirpation). Patient 2 had an advanced non-resectable supraanal rectal carcinoma. Both tumours are shown in Figures 5–7.

The hyperthermia planning system

For both patients CT scans of 1 cm slice thickness were performed—a total of 60 sections. Segmentation of the CT data sets, i.e. specification of different tissue compartiments (muscle, bone, fat, tumour etc.) is carried out interactively via contour input using TOMAS (‘tool for manual segmentation’, developed at the Cancer Research Centre at Heidelberg, FRG, see [24]). A tetrahedral grid is created from these contours as described by Seebass et al. [20].

Calculation of the electric field is performed using the VSIE method [18]. This method was developed to produce exact numerical calculations regarding the field behaviour at electrical interfaces. Fields can be calculated for any geometrical combination of interfaces, including ones in which more than two media meet at a corner or edge [19]. The assumed electrical characteristics (relative dielectric constant ε_r and conductivity σ in S/m) of the tissue are displayed in Table I. The antennas are assumed to be dipolar with a sine shaped current distribution. Deionised water is taken to be the homogenous background medium, which is the only way reasonable calculation times can be achieved (see below). In principal the use of water as a background medium does not affect the general validity of the results. However, in this way derived results of optimisation studies might be too optimistic, at least for the presently used applicator SIGMA-60 which has a reflective boundary between bolus filling (deionised water) and surroundings (air). This interface effects that Ε field control is worse than predicted by simulation studies based on a homogeneous background medium water.

The VSIE method is based on an integral equation with a volume and a surface term. The resulting multidimensional linear system is characterised by dense non-symmetrical matrices. This is solved iteratively with the GMRES solver (general minimum residuum method). On average, 60 iterations are required. Storage capacity for 40 000 tetrahedrons (8000 grid points) is approximately 120 MB and the calculation time using a SUN Sparcstation 10 is 6–8 h.

Table I.  Tissue parameters for optimization studies with Π and Θ. Perfusions are shown for the condition ‘low’, ‘medium’, ‘high’ (from left to right), concerning the tumour perfusion.

Tissue	Conductivity (1/Ωm)	Perfusion wb (ml/100 g/min)	Temperature limit (°C)
Tumour	0.8	5, 8, 10	55
Muscle	0.8	20, 15, 15	44
Intestine	0.8	20, 20, 20	42
Fat	0.04	5, 5, 3	44
Bone	0.02	5, 5, 3	44

Temperature distribution is calculated by numerically solving the bio-heat transfer equation (BHTE). The assumed values for tissue perfusion are on the optimistic side as shown in Table I: perfusion in normal tissue reactively raised in comparison to basal values at 5 ml/100 g/min (fat, bone) or 20 ml/100 g/min (muscle), resp.; whereas the perfusion in the tumours, which have a decreased capacity for thermoregulation, is on the low side at <10 ml/100 g/min. The assumed values represent mean values from analyses of clinical temperature-time curves [7].

For calculation of the temperature distribution the stationary BHTE is solved using the KASKADE program system [25]. This involves a finite element algorithm which is based on the same tetrahedron grid as the VSIE algorithm. The temperature calculation also requires the solution of a linear equation system, but whose matrix is sparsely occupied. This equation system is solved iteratively using a preconditioned, conjugated gradient process. The KASKADE program system also allows adaptive refinement of the grid based on an error estimator [26], [27]. For the present study use of the course grid proved as sufficient. The calculation time on the coarse grid is about 5 s (SUN Sparc 10). As part of the preparation of the temperature optimisation, temperature distributions must be calculated for several different power distributions (n² power distributions for n independent channels). This means that the linear equation system has to be solved with the same matrix for several different right sides. CPU time per right side for the iterative process is around 1.4 s. For n ⩾ 0, it is worth solving the equation system directly. To do this, we perform a Cuthill-McKee renumbering of the nodes in order to keep the matrix fill-in as small as possible [28]. The matrix is decomposed using the Cholesky Method. This brings down the CPU time to <1 s per right side (SUN Sparc 10).

Several methods were implemented or developed for the integrated visualisation of the CT data sets with contours, Ε-field, SAR and temperature distributions (T):

• CT image information in three planes (transverse, frontal and sagittal) together with superimposed iso-SAR(T)- lines or SAR(T)- shaded areas [29], optional superimposition of contours (particularly those of the target volume) (Figures 5–6).

• Vector representation of the Ε-field distribution in three planes together with contours or CT image information (Figure 7).

This kind of graphical representation is used for initial quality assessment and as an aid for visualising physical and clinical correlations (e.g. identifying local E-field maxima as the reason for hot spots).

Quantitative evaluation is provided by the analysis of temperature distribution using a temperature-volume histogram from which the index temperatures T_x are taken. T_x represents the temperature reached or exceeded by x% of the tumour volume (or measurement points).

SAR optimisation

The following power related (Π objective functions (descriptors) were defined as shown in Table II:

• Π₁: ratio between the mean power absorbed in the tumour and the mean power absorbed outside the tumour.

• Π₂: ratio lisbetween the mean power absorbed in the tumour and a specified number (e.g. 10) of local power maxima outside the tumour (that possibly result in hot spots).

• Π₃: by analogy to Π₁, but in the denominator power densities SAR are squared resulting in an increased weight of local SAR maxima.

• Π₄: by analogy to Π₁, but power densities SAR are replaced by SAR/perfusion w_b, considering that the temperature increase at a point is approximately proportional to the quotient SAR/w_b.

• Π₅: by analogy to Π₂, but power densities SAR are replaced by SAR/perfusion w_b. Π-descriptors are maximized using a modified gradient method according to Fletcher and Powell [30].

Table II.  SAR-related and temperature-related objective functions for the optimisation procedures (SAR: specific absorption rate in W/kg, T_lim temperature limit depending on tissue type, see table I).

SAR-related objective functions:

Temperature-related objective functions:

Optimisation using the descriptor Π₁ can also be formulated as a generalised Eigenvalue problem [31]. The absolute maximum is then derived faster by finding the maximum Eigenvalue. Unfortunately, the optimisation variable Π₁ does not provide clinically suitable solutions for SAR distribution (see Section 3), which means this method is of no practical value.

Temperature optimisation

In general, each tissue compartment has a specific temperature limit as shown in Table I (‘switch-off ’ conditions). By definition, they are not used on the surface of the tumour (boundary with healthy tissue). Within these constraints, the following objectives have been set:

1. temperature in the tumour should be ⩾43°C;

2. temperature in healthy tissue should be ⩽42°C.

Areas in which the temperature distribution deviates from these objectives are ‘penalised’, i.e. the squares of the deviations from the desired values are added up. The descriptors Θ₁ and Θ₂ (see Table II) are denned according to these rules. Θ₁ is dependent on the first objective only, whereas Θ₂ is dependent on both objectives. The aim is to search for a minimum value of Θ_1/2.

The optimisation of a descriptor analogue to Θ₂ is described in Nikita et al. [32], in which a damped Newton procedure was used. In every iterative step, the first and second derivatives of Θ according to the parameters (amplitude and phase) have to be calculated. If temperature distributions corresponding to n² SAR distributions have already been calculated (see above), these derivatives can be determined exactly (without numerical differentiation) and very quickly.

This optimisation method does not work if additional temperature limits are set. If so, we are dealing with a constrained optimisation process, which in our experience is particularly susceptible to find a local minimum instead of the global optimum. If we weaken the strictness of these temperature limits, the constrained optimisation can be approximated by an unconstrained optimisation procedure. In this case, a further term is added to Θ₂, defining a temperature T_lim-ε slightly below the true temperature limit and weighting a violation by a factor W ≫ 1. Then, the resulting descriptor (see Table II) is used for optimisation as described [32]. Suitable values for W and ε are 50 and 0.2°C. This kind of optimisation procedure proved as highly efficient to approach the global minimum.

CPU times for temperature optimisation, including n² temperature calculations (see above) are about 8 min for 12 channels, and 25 min for 24 channels (SUN Sparc 10). However, they rise to 12 h for 12 pairs of antennas if variations of inclinations are additionally considered since the derivatives according to the inclinations cannot be calculated analytically.

Design of the simulation study

The aim of this simulation study is to assess both the technical feasibility of regional hyperthermia with the available BSD-2000 system and the possibilities for improvement by upgrading the system in the following ways: number of antennas, number of channels (with phase and amplitude control) and variation of the inclination of the antennas, which is assumed as the most relevant of all the geometrical degrees of freedom. Other geometrical degrees of freedom such as antenna coordinates could not be systematically taken into account because of the calculation times involved, as a new field calculation has to be carried out for every change in a geometrical antenna parameter.

Figure 1 is a schematic representation of the transition from the simplest antenna arrangement (corresponding to the clinically used SIGMA-60) to the most complicated arrangement (three rings with eight antennas per ring arranged in parallel along the patient axis).

Figure 1. Schematic representation of the SIGMA ring applicator (four antenna pairs, left) and its upgrade by increasing the number of antennas in a three-dimensional set-up (24 antennas, three rings in parallel, right). Both antenna types are matched to 90 MHz per constructionem (see text).

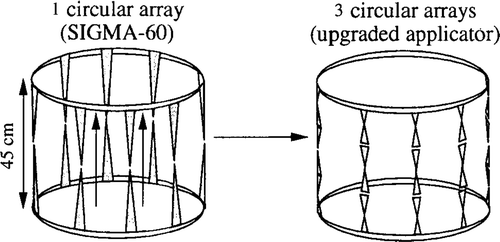
All calculations were performed at the fixed frequency 90 MHz. Lengths of dipole antennas in the SIGMA-60 applicator are 45 cm, while the antennas are placed at the air/water boundary of the applicator. For the triple ring applicator, dipole lengths are shortened to 15 cm by embedding the antennas into the bolus medium, i.e. water. Therefore, antennas of both applicators are matched to 90 MHz, and a sine-shaped current distribution may be assumed on every type of antenna.

The following system upgrades were studied with respect to their potential benefit for regional heating (explaining the abbreviations in Figures 2, 3):

• syn, 1 × 4p: eight antennas circularly arranged are fed synchronously or in pairs by four independent channels, according to the SIGMA-60 applicator;

• 1 × 8: same circular arrangement, but every single antenna controlled in phase and amplitude (eight channels);

• 3 × 4p: 24 antennas arranged in three rings (Figure 1, right), fed in pairs;

• 3 × 4p + incl: an additional rotation of every antenna pair is simulated in the plane generated by the axes of the antenna pair and ring;

• 3 × 8: all 24 antennas are independently controlled in phase and amplitude.

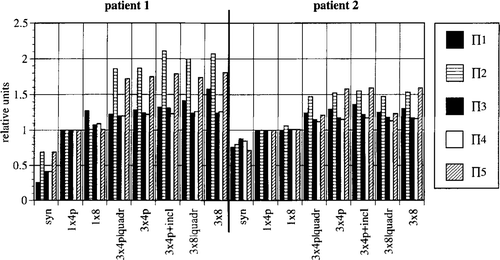
Figure 2. Change in power-related optimising variables Π_i (i = 1, …,5) in relation to levels of system upgrade, for patient models 1 and 2. Relative values for Π_i are shown normalised throughout for the optimized condition of the standard system SIGMA-60 (1 × 4p).

The costs of the applicator are predominantly determined by the number of power amplifiers. Therefore, additional ‘low cost’ variants of the 3 × 4p or 3 × 8 configurations are investigated which are realized with four (instead of 12 or 24) power amplifiers:

• 3 × 4p|_quadr: every three antenna pairs of a quadrant are fed by one of four power levels of choice. However, the phase of every pair is independently controlled by a phase shifter (i.e. 12 phases);

• 3 × 4p|_ampl: three arbitrary antenna pairs are fed by one of four power levels, i.e. the linkage between antenna pair and power is optional. Again 12 free phases;

• 3 × 8|_quadr: six antennas of a quadrant are fed by one of four power levels whereas 24 independent phases are available;

• 3 × 8|_4ampl: six arbitrary antennas are fed by one of four power levels whereas 24 independent phases are available.

Figure 3. Change in index temperature Τ₉₀, tolerated absorbed total power and volumetric stress on the normal tissue (⩾42°C) with system upgrading, after direct optimisation of temperature distribution using the Θ₂ objective function (Table II) for patient models 1 and 2.

Results

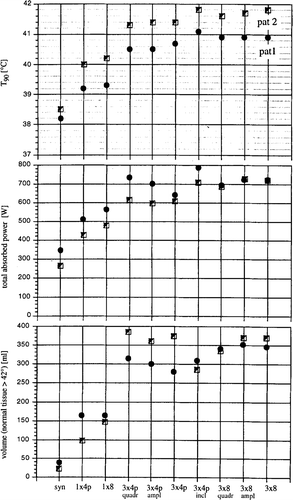
The power related descriptors Π_1–5 (Figure 2) and the parameters T₉₀ (index temperature), Ρ (tolerated total power absorbed in the patient) and V₄₂ (volume of normal tissues with temperatures above 42°C) that were optimised with Θ₂ were determined as a function of the system upgrade (number of antennas, number of channels and inclination of antennas) (Figure 3). Additionally, the dependence of the results (T₉₀) reached by optimisation on the particular choice of perfusion conditions, and the stability against phase inaccuracies, as well as the temperature distributions achieved by maximization of the descriptors Π_1–5 were investigated (Figure 4). Note that the results are related to the absorbed power, and do not depend on the radiation efficiency of the antennas.

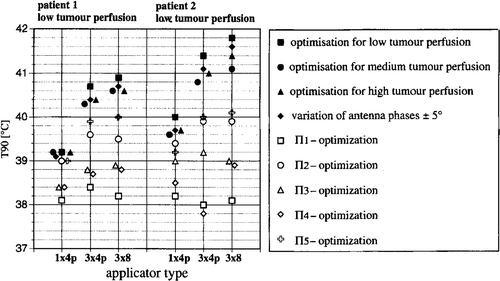
Figure 4. Change in index temperatures T₉₀ with system upgrade for patient models 1 and 2 after: Optimising Θ₂ for three different perfusion models as specified in Table I and using the derived ‘optimised’ power distribution for one of the models (with low tumour perfusion); Varying of antenna phases by ±5°; Maximising the power-related descriptors Π_i (as shown in Table II). The power distributions produced with the latter result in significantly worse temperature distributions.

Optimisation according to the power distributions

The increases in Π_1–5 with system upgrade are illustrated in Figure 2 (normalised throughout for the standard system with four pairs of antennas).

Patient 1 (high presacral rectal carcinoma) benefits more than patient 2 (supraanal rectal carcinoma). The tumour in patient 1 is difficult to heat due to its anatomical position (it is shielded by the pelvic bone) so the possibilities for improvement by upgrading the system in this case are particularly good. The descriptors Π_2/5 show the greatest increases (by 100% for patient 1; by 50% for patient 2). It is obvious that additional degrees of freedom are necessary, particularly for the minimisation of hot spots. Changing from 1 × 4 antenna pairs (one single ring) to 3 × 4 antenna pairs (three rings in parallel) results in a large increase in Π_2/5. In contrast, additional variations in the orientation of the antennas result in only small improvements (increase in Π in the order of 10%).

The optimisation of the SAR distribution using Π does not however necessarily result in a similarly improved temperature distribution (see Figure 4 for the corresponding intratumoural values for T₉₀). Π₁,₃,₄ proved to be completely useless for clinical purposes because of the general tendency for hot spots to occur even with low power levels. Π₁ has been used by several groups of workers as an optimising variable [33–35]. Wust et al. [10] showed that in two dimensions, power distributions obtained by maximisation of Π₁ are suitable provided that total power is low. Although high SAR values are weighted in the formulation of Π₃ and perfusions are taken into account in Π₄, the temperature distributions achieved with these descriptors are no better. Π_2/5 are more suitable as optimising criteria for SAR distributions as they are specifically formulated to reduce hot spots. The perfusion related discriptor Π₅ is the best for this, although it is still clearly inferior to direct optimisation of the temperature distribution. A descriptor similar to Π₂ was used by Richards [36].

Optimisation according to the temperature distributions

Direct optimisation of the temperature distribution using Θ descriptors is superior to all methods that adapt power distribution, as shown by the T₉₀ curve in Figure 3 for Θ₂ (Τ₂₀ and T₅₀, which are not shown, show similar changes). The temperature distributions achieved using Θ₁ are in general no more effective than those achieved using Θ₂. However, the normal tissues are heated to a significantly greater extent. For this reason we will consider only Θ₂ in the following.

In patient 1 (high presacral) there was a significant increase in T₉₀ when 3 × 4 antenna pairs were used instead of 1 × 4 (∼1.5–2°C increase in the index temperatures). A smaller but still significant increase was made possible by further increasing the number of channels to 3 × 8 = 24 (an additional ∼0.3–0.7°C). Comparing the single ring (SIGMA-60, 1 × 4 antenna pairs) to the fully upgraded system (3 × 8 antennas), T₉₀ (corresponding to the minimum temperature) increased from 39.2 to 40.9°C and T₂₀ (corresponding to maximum temperature) increased from 40.5 to 43.5°C (for a tumour perfusion of 5 ml/100 g/min). Total power can be increased from 510 to 720 W without exceeding the temperature limits (Table I). A slight advantage in effectiveness (41.1 versus 40.9°C for T₉₀) is achieved if additional variation of the antenna inclinations are assumed.

In patient 2 (supraanal) there was also a large increase in T₉₀ when switching from 1 × 4 antenna pairs to 3 × 4 antenna pairs (∼l.2–l.8°C increase in the index temperatures). Increasing the number of channels from 3 × 4 antenna pairs to 3 × 8 antennas results in only small increases in effectiveness of ∼0.2–0.4°C.

It seems easier to treat patient 2 with regional hyperthermia than patient 1, as a higher effectiveness (T₉₀ = 40.0 versus 39.2°C) is possible despite lower power (420 versus 510 W), even when using the single ring (corresponding to the BSD-2000).

When the presently available BSD-2000 system is fully upgraded with the maximum number of antennas and channels, the total improvement achieved is: T₉₀ increases from 39.9 to 41.8°C, T₂₀ from 42.9 to 45.3°C and Ρ can be increased from 420 to 720 W (with a tumour perfusion of 5 ml/100 g/min). Consequently the benefit of system upgrading for patient 2 (2.0–2.4°C temperature increase) is comparable to patient 1 (1.7–3.0°C, see above). No effectiveness is added by variation of antenna inclinations (compared with 3 × 8 antennas in fixed geometry).

Total power

Figure 3 also shows how the tolerated total power absorbed is related to system upgrade; the maximum limit of tolerance is defined as a tissue-specific temperature, as shown in Table I. Higher intratumoural temperatures are clearly correlated with higher total power. The increase in total power is made possible by the reduction of hot spots using the optimisation process. Accordingly the greatest possible increase in total power is again achieved by increasing the number of antenna pairs from 1 × 4p to 3 × 4p. For patient 1, using the single ring (1 × 4p, 1 × 8), up to 100 W or more power is needed despite nearly 1°C lower temperatures (the tumour is difficult to heat). Interestingly, the gain of effectiveness (T₉₀) is in the same range for both tumour sites as the system is upgraded, i.e. around 1.7°C for an upgrading from 1 × 4p to 3 × 8 antennas.

Normal tissue

Figure 3 shows in the lower part the thermal stress on the normal tissues (V₄₂, volume of normal tissue >42°C) depending on system upgrade. Higher temperatures and homogenous temperature distributions are unavoidably associated with higher temperatures in the normal tissues due to the increase in total power.

It is notable that, for both patients, the most complicated stage of system upgrade to 3 × 4 antenna pairs with variable inclination leads to an increase in tolerability (e.g. for patient 2 reduction in V₄₂ from 370 to under 285 ml of normal tissue at temperatures greater than or equal to 42°C, Figure 3) with even a small increase in effectiveness (see T₉₀). Thus increased flexibility allows easier spatial concentration of SAR. Increased tolerability can be clinically important in a similar fashion to the increased efficacy.

Stability of solutions with regard to variations in perfusion and phases

Figure 4 shows that solutions optimised using Θ₂ for different perfusion conditions (low, medium, high perfusion according Table I) result in comparable temperature distributions at one particular perfusion condition. To be specific, if a solution optimized for the perfusion condition ‘high’ is applied for the alternate perfusion case ‘low’, it results in a drop in T₉₀ of only 0.3–0.7°C if compared with the solution optimised for the correct perfusion case (here ‘low’). This deterioration is small compared with the changes seen when different optimising strategies (e.g. Π descriptors, see Figure 4 open symbols) are used.

If a phase error of ±5% is assumed for an antenna setting, slight decreases of <0.3°C are seen in T₉₀ for the optimised solution. Based on these model calculations for practical applications, we have concluded that the solutions arrived at with an optimising strategy are adequately stable under parameter variation.

Characterisation of power and temperature distributions

Figure 5 shows the change in SAR distribution, which has been optimised using Θ₂, in tumour model 1 (in sagittal section) for the change from the 1 × 4 antenna pairs configuration (SIGMA-60) to the upgraded system of 3 × 8 controllable antennas. The areas at risk from hot spot formation lie dorsally at the level of L5/S1 and with an even higher risk ventrally in the pre- and suprapubic areas. Optimisation according to Θ₂ for the upgraded system results in a smearing of excessive SAR, i.e. a dissemination of the power over a larger volume.

Figure 5. Power distribution (sagittal section, colourwash representation) after optimisation with Θ₂ for tumour model 1 (high presacral), using the commercially available SIGMA-60 applicator (left). Hot spots at the dorsal sacral bone and at the symphysis. Only little power in the tumour. The power distribution using the upgraded triple-ring applicator (24 antennas according to Figure 1) is shown on the right. Hot spots are considerably reduced. Power in the tumour is clearly increased. Numbers on the left represent percentages of the maximum of the power distribution, corresponding to different colours.

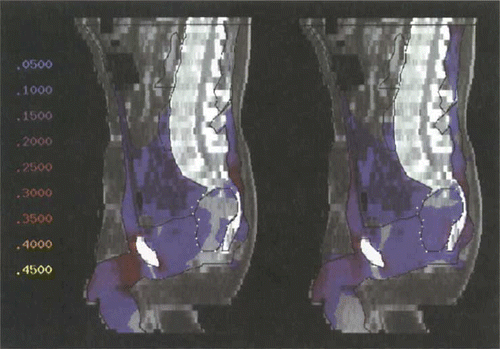
The SAR distribution within the tumour is hardly affected by this. There is no focusing (contrary to popular belief). In fact, an increase in total power is made possible due to the homogenisation of the SAR distribution in the total volume (hot spot reduction).

The temperature distributions (Figure 6) are influenced to a surprising extent by this SAR modification. The change from 1 × 4 antenna pairs to 3 × 8 antennas results in a redistribution of the temperature maximum further into the tumour with simultaneous reduction in the temperature peaks in the normal tissue. The total thermal stress on the lower abdomen does however increase (see discussion).

Figure 6. Temperature distribution (sagittal section, colourwash representation) after optimisation with Θ₂ for tumour model 1 (high presacral), using the commercially available SIGMA-60 applicator (left). High temperatures suprapubically and dorsally. In comparison, temperature distribution using the upgraded triple-ring applicator (24 antennas according to Figure 1) is shown on the right. Temperature in the tumour has significantly increased. However, higher temperatures are distributed throughout a larger area of normal tissue. Numbers on the left represent temperatures [°C], corresponding to different colours.

Figure 7 shows the adaptation of the electric field in tumour model 2 (distally located rectal carcinoma) by means of a vector diagram. The heating of this tumour is fairly good for clinical purposes, even with the SIGMA-60 applicator, but if the optimising process is used the total power can be nearly doubled (400–700 W) to produce an increase in T₉₀ of almost 2°C (Figure 3).

Figure 7. Electric field distribution (sagittal section, vector diagram) after optimisation with Θ₂ for tumour model 2 (distal supraanal), using the commercially available SIGMA-60 applicator, shown on the left. In comparison, electric field distribution (sagittal section, vector diagram) after optimisation with Θ₂ for tumour model 2 (distal supraanal), using the upgraded triple-ring applicator (24 antennas), shown on the right. Significant changes of the electric field vectors in size and direction are seen at the dorsal sacral bone reducing the hot spot. Such an Ε field control is based on appropriate phase selections in longitudinal direction of the triple-ring applicator.

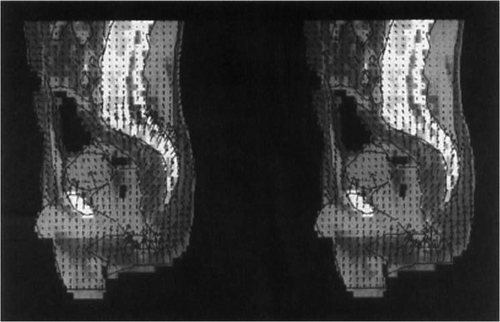
This increase in power is made possible by a smoothing out/reduction of all SAR maxima, in particular in the anterior abdominal wall and in the area of the pelvic floor. Similar to patient 1 in Figure 5, the result of this SAR modification is a ‘concentration’ of the temperature in the tumour and the surrounding tissues (not shown).

Discussion

Despite difficulties in practice, regional RF hyperthermia is already feasible in certain clinical situations. However, efficacy and tolerability must be increased.

This computer simulation study shows that it is possible to achieve a qualitative increase in efficacy by upgrading existing hyperthermia systems. This improvement is due to an increase in the number of antennas which results in particular in the ability to influence the Ε-field distribution in the direction of the patient axis by selecting appropriate phase values. We have extended therapy into the third dimension (z-direction), which has not been possible with any system until now, by considering a three-dimensional arrangement of three antenna rings in parallel instead of one (Figure 1). The estimated improvement in clinical efficacy associated with this system expansion is highly significant, with increases in index temperatures of 1–2°C.

Naturally the possible improvement due to system upgrade depends on tumour site and perfusion conditions. High presacral tumours (usually recurrences of rectal carcinoma, tumour model 1) are known to be difficult-to-heat tumours [5], [6], and these gain particular benefit from the increase in number of antennas and channels.

Distally situated (supraanal) rectal carcinomas, on the other hand, can be heated already quite well using existing technology. However, performance can be greatly improved by refined application techniques.

These results, which could only be achieved after a long development of a hyperthermia planning system (Table III), are revealing and encouraging for technical advancement. The numerical and programming details will be described in a future paper.

Table III.  Modules of hyperthermia treatment planning shown with present expense of time at a SUN Sparc 10 workstation

In the past, some researchers have called radiofrequency hyperthermia using existing techniques unpromising and unpredictable. This is understandable in the light of this study, particularly when one considers the simplicity of the systems which are in clinical use.

Further research is needed to determine whether the calculated distributions obtained using an optimising process can be achieved technically, and put into practice in the clinical situation.

Reflection from the applicator surface (interface between bolus filling and surrounding air) and coupling between antennas have so far not been included in the simulation calculations. Neither of these factors can be ignored when using the original version of the SIGMA applicator. Because these effects compromise the control of SAR distributions, they should be reduced as far as possible for a new designed applicator. The following measures were recently introduced or suggested: ferrite shields around the power supply cables and broadband control couplers to suppress radiation reflecting back into the amplifier (Turner, personal correspondence 1994), introduction of special synthetic resin-based applicator materials for damping and suppressing reflection [8], insertion of imperfect dielectric structures/media to lower the Q-value.

To achieve a more realistic description of radiofrequency hyperthermia we are planning to incorporate the effect of antennas (and their mutual interaction) into the numerical calculations. Improvements can also be achieved through antenna base measurements of phases and amplitudes (e.g. electro-optical, 12), which are integrated into the model.

The way the optimisation problem is solved should not be too dependent upon details of the anatomy or positioning of the patient. Future research will include performing systematic uncertainty analyses, and studying other tumour models by using the planning system and making comparisons with clinical observations.

The limited existing experience shows that the SAR distributions arrived at through the optimising process are not particularly dependent on patient-specific input parameters—neither perfusion nor minor anatomical details. It appears rather that a continuum of phases and amplitudes results in comparable (clinically equivalent) SAR distributions, and this increasingly so with greater numbers of antennas and channels. Thus there is a certain stability inherent in the problem with regard to translation into clinical practice, and we hope therefore to be able to develop standardised settings for the individual tumour locations.

The results of this simulation study give grounds for optimism regarding the potential of RF technology, justifying further technological development and clinical testing of radiofrequency techniques in future research.

Acknowledgements

The authors thank Paul Turner, M.S., very much for stimulating discussions and helpful suggestions. This work is supported by the Berliner Sparkassenstiftung Medizin, Deutsche Krebshilfe e.V. (Grant M7/94/Fe 9) and Deutsche Forschungs gemeinschaft (SFB 273). We would like to dedicate this publication, with our heartfelt thanks, to Professor Dr Robert Fischer on the occasion of his 65th birthday.

Declaration of interest: The authors report no conflicts of interest. The authors alone are responsible for the content and writing of the paper.