Fundamental solutions to the bioheat equation and their application to magnetic fluid hyperthermia

Abstract

Methods of predicting temperature profiles during local hyperthermia treatment are very important to avoid damage to healthy tissue. With this aim, fundamental solutions of Pennes’ bioheat equation are derived in rectangular, cylindrical, and spherical coordinates. The medium is idealised as isotropic with effective thermal properties. Temperature distributions due to space- and time-dependent heat sources are obtained by the solution method presented. Applications of the fundamental solutions are addressed with emphasis on a particular problem of Magnetic Fluid Hyperthermia (MFH) consisting of a thin shell of magnetic nanoparticles in the outer surface of a spherical solid tumour. It is observed from the solution of this particular problem that the temperature profiles are strongly dependent on the distribution of the magnetic nanoparticles within the tissue. An almost uniform temperature profile is obtained inside the tumour with little penetration of therapeutic temperatures to the outer region of healthy tissue. The fundamental solutions obtained can be used to develop boundary element methods to predict temperature profiles with more complicated geometries.

• bioheat equation
• cancer treatment
• ferrofluids
• fundamental solutions
• hyperthermia

Introduction

Local magnetic hyperthermia for cancer treatment using magnetic particles has been considered since 1957. Gilchrist [1] studied this type of treatment by injecting small particles (around 1 µm) of a magnetic iron oxide in the lymph nodes of animals, obtaining differential heating upon application of an oscillating magnetic field. This treatment relies on the fact that maintaining cells at a temperature between 42° and 45°C results in damage to proteins, inducing cell death.

In order to ensure that high temperatures are localised in tumours and not in the surrounding healthy tissue, predictions of the temperature profiles achievable during treatment are needed. The aim of these predictions is to define the optimum values of parameters such as magnetic field intensity, frequency and volume fraction of magnetic particles, among others.

The mathematical model for heat diffusion in biological tissues adopted in this study is the model proposed by Pennes [2] in 1948 and is referred to as the bioheat equation. This equation is, basically, the result of performing an energy balance on a control volume in stationary media assuming it is homogeneous and isotropic. This is an ‘effective medium model’ in which the whole domain is regarded to have effective thermal properties. A significant fraction of the work done dealing with heat transfer in living tissues for magnetic fluid hyperthermia (MFH) applications involves Pennes’ bioheat equation [3–7]. Other mathematical models for obtaining the temperature distribution known as discrete vasculature models (DVMs) were developed after Pennes [8], [9] but the complexity of these models (information about the vascular network is needed) and the applicability of Pennes’ equation in regions with small vessels make this model a good candidate for bioheat studies.

There have been various recent studies whose objective was to understand and characterise heat transport in biological tissues for MFH applications. Andrä et al. [10] solved a one-dimensional (1D) transient problem of a spherical tumour, using the Laplace transform, with a constant heat source embedded in an infinite medium but neglecting blood perfusion in either region. Bagaria and Johnson [7] used the separation of variables technique to obtain a solution for two concentric spherical regions where the smallest had energy dissipation due to a polynomial distribution of nanoparticles in the radial direction. Although useful for characterising heat transfer for different spatial particle distributions, the resulting solution is rather complicated. Additionally it is very difficult in practice to obtain the prescribed polynomial spatial distributions of nanoparticles used in their analysis. Durkee et al. [11] presented solutions to a 1D transient problem consisting of contiguous regions with different thermo-physical properties in spherical and Cartesian coordinates. Pennes’ bioheat equation was used to model heat transfer in each region and the set of equations was coupled through boundary conditions at the interfaces. The evaluation of the Eigen values and the subsequent determination of the integration constants is complex. This solution is useful if steep changes exist in the properties of the domain around the area of analysis but this is rather difficult to obtain in practice. Commonly, values for the thermal properties vary very little for different types of tissues [12]. Perfusion though, does change a lot between patients, and within a single treatment demanding a quantification of its effect [13]. By using the same technique, Durkee and Antich obtained an exact solution in cylindrical coordinates [14]. Finally, Durkee and Antich extended the solutions of their earlier work to incorporate time-dependent heat sources and boundary conditions but with homogeneous heat sources [15].

Previous work using Green's functions as a tool for solving bioheat problems includes the work of Gao et al. [16] who solved the 3D transient bioheat equation using Cartesian coordinates in an unbounded domain and proposed the use of the Fourier transform as a method for solving the convolution integrals in the expression for the temperature in terms of Green's functions. They argued that the remaining integral is known in most cases but the most difficult part lies in taking the inverse of the transformation to go back from the Fourier domain to the spatial domain. Vyas and Rustgi [17] presented a solution in cylindrical coordinates for an unbounded domain exhibiting axial symmetry. The heat source in their analysis is modelled as a laser pulse centred on the z-axis and whose intensity varies as a Gaussian distribution in the radial and axial directions. Deng and Liu [6] developed two Green's functions for solving a bioheat transfer problem where the heat source can be time-dependent as well as space-dependent. They based their study in a finite region of tissue in Cartesian coordinates. These solutions are interesting to analyse heat diffusion in radio frequency (RF) heating of the skin. They also studied the case of point sources combined with skin cooling. Although these fundamental solutions to the bioheat equation exist they have limited applicability to MFH.

The aim of this contribution is to derive fundamental solutions for the linear bioheat differential operator in rectangular, cylindrical, and spherical coordinate systems and show how these can be used in bioheat problems. Using these fundamental solutions a large number of problems may be solved. Particular solutions for finite domains subjected to boundary conditions of any kind may be further developed, illustrating the advantage of Green's function method for solving these types of heat diffusion problems. These fundamental solutions can also be used as weighting functions for developing boundary integral methods to simulate energy dissipation in practical settings.

In practice, a method for solving the temperature profiles for arbitrary distributions of particles is needed in order to be able to control the temperature distribution inside the tumour and the surrounding healthy tissue. One approach could be the development of an algorithm which uses MRI to visualise the distribution of the particles and by means of superposition of fundamental solutions predicts the temperature profile produced by the observed spatial distribution of particles. Then, changes in magnetic field parameters may be carried out in order to make corrections to the heat generation pattern [18]. Also, information regarding perfusion features of the surroundings of the tumour can be assessed with the aid of dynamic contrast-enhanced MRI [19].

Fundamental solutions

The Green's function for a given partial differential equation and corresponding initial and boundary conditions is the response of a system to the action of a unit of instantaneous heat pulse acting at an arbitrary point r′ at an arbitrary time τ. The term ‘instantaneous’ indicates that the source (in this particular case, the heat source) releases all its heat spontaneously at a time τ in a point r′ within the domain. Mathematically, the Green's function is the solution to the partial differential equation defined by the same linear operator as the original problem but with an inhomogeneous term in the differential equation corresponding to the instantaneous point source and with initial and boundary conditions that are homogeneous versions of the original conditions. If the extension of the domain is infinite, the Green's function is called the fundamental solution or free-space Green's function.

Governing equation

The bioheat equation, assuming constant thermal properties and an isotropic medium, is given bywhere X = (x₁, x₂, x₃) represents the position vector; ρ, c, and k are the effective density, specific heat and thermal conductivity of the tissue; ρ_b and c_b are the density and specific heat of blood; ω_b is the blood perfusion rate; T_a is the arterial temperature, which is assumed to be constant due to self-regulation of metabolism; q_met is the volumetric heat generation due to the basal metabolism, regarded as uniform within the tissue; Q_gen is the volumetric heat generation due to the nanoparticles; and T is the tissue temperature.

A more convenient form of Equation 1 is obtained by defining a new variable and introducing the bioheat linear differential operator L. Substitution yields:where is a constant which characterises the blood perfusion rate, (), is the thermal diffusivity of the tissue, and is a generalised heat source.

Fundamental solutions for the bioheat operator

In order to find a fundamental solution for a particular linear differential operator, an equation such asmust be solved, where is a Green's function and δ is the Dirac delta. As mentioned before, if the domain is unbounded the Green's function is usually called the fundamental solution and is denoted here by . Thus, given the fundamental solution along with the initial condition, the temperature profile in an infinite domain is obtained from the Green's function solution equation (GFSE) for any space- and time-dependent heat source and initial condition. The importance of the fundamental solution is that it can be used to obtain the Green's functions (i.e. through the method of images) and that it forms the set of basis functions for numerical methods, such as boundary element methods (BEM) [20].

In the following sub-sections the mathematical formulation of the free-space Green's function problem for the bioheat operator is set for the three coordinate systems, after which the GFSE for one-dimensional problems in infinite domains is presented. For the sake of brevity, the detailed derivation is shown only for Cartesian coordinates and the other two derivations can be found in Appendices A and B.

Cartesian coordinates

Mathematically, the fundamental solution for a 1-D problem in Cartesian coordinates is the solution of the equationIn order to find U, the Fourier transform with respect to the spatial coordinate is used to eliminate the spatial variable and thus obtain an ordinary equation in time. The notation and mathematical form used here for the transform and its inverse areTransforming both sides of Equation 4 one obtainsNote that the right hand side of Equation 7 is zero for either or , so we have two conditions for In order to relate both solutions in Equation 8 and to incorporate the singularity in t = τ produced by the Dirac delta, integration is performed in Equation 7 with respect to t from τ - ε to τ + ε with ε as an arbitrarily small parameter. This yields, in the limit On the other hand, from (4) U = 0 if , then and A = 0 from Equation 8. Thus and replacing in Equation 8Taking the inverse Fourier transform, the so called fundamental or free space solution for the bioheat differential operator, U, is given by:where is the Heaviside unit step function.

Cylindrical coordinates

Following the same procedure shown above it is possible to obtain the fundamental solution for the bioheat differential operator in cylindrical coordinates. The detailed derivation is shown in Appendix A. The result, obtained by using the Hankel transform and then solving the resulting ordinary differential equation, iswhere is the modified Bessel function of the first kind.

Spherical coordinates

In this case, the differential equation to be solved in order to obtain the fundamental solution is:The procedure for obtaining the solution is different from that used for Cartesian and cylindrical coordinates. For the details see Appendix B. After solving Equation 13, the principal solution for the spherical coordinate system is found to beThe integral in Equation 14 has a closed analytical form. The final expression for the fundamental solution is

Green's function solution equation

The Green's function solution equation (GFSE) is a general expression which allows obtaining the temperature distribution in a medium provided the Green's functions or the fundamental solution (case of unbounded domains) plus suitable initial and boundary conditions are given. For the particular case of Equation 1, characterised by the operator L, the GFSE is given bywhere is the fundamental solution evaluated at is the initial condition; is the generalised heat source (sink/source), which may vary in time as well as in space; α is the thermal diffusivity of tissue; and is a weighting function for which the exponent p is:

Application

In this section, the temperature profile due to a spherical shell source is presented as an example of the application of the GFSE. The outer region extends to infinity. Such distribution of the magnetic particles during MFH is possible if specific binders are attached to the surface of the nanoparticles during their synthesis [21], [22]. When injected into the arterial supply of a tumour, the particles are preferentially ingested by the diseased cells located at its surface. This process is favoured by the structure of solid tumours: they have a dense core with decreasing vessel sizes when moving to its nucleus [23].

A brief description of the initial and boundary conditions is presented first. Then the mathematical formulation along with its solution using the fundamental solution Equation 15 is presented.

Initial and boundary conditions

It is considered that initially the whole domain is at the core body temperatureThis is a good approximation since deep tissue is almost constantly kept at 37°C by metabolic regulatory mechanisms.

Considering that solutions for unbounded domains are developed in this work, the boundary conditions are such that the temperature far from the region of interest approaches the core body temperature. Thuswhere s stands for the spatial variable of any of the three coordinate systems considered here.

Mathematical formulation

As a mathematical model, an enclosed spherical region models the diseased tissue and is surrounded by a thin shell of magnetic nanoparticles. The outer region extends to infinity and represents the healthy tissue. The thermo-physical properties are regarded to be constant in both regions.

The temperature distribution is given by the one-dimensional version of Equation 1 in spherical coordinatesThe boundary and initial conditions are given by Equations 21 and 22 respectivelyThe mathematical representation of a shell source of strength (W) releasing its energy at r = r₀ continuously from time t = 0 isThe solution to this problem is obtained by using the fundamental solution Equation 15 and the GFSE Equation 16 with p = 2, and The integral can be integrated analytically for the source given in Equation 23. Replacing the expression for given in Equation 15 and from Equation 23 one obtains:The integral also has an analytic solutionSubstituting the partial results of Equations 25 and 26 into Equation 24, the solution for is expressed as:

Results and discussion

For purposes of plotting the results, the values for the thermo-physical properties of blood and tissue were taken from the literature [12]: , , , , , . Each curve in the graphical solution was obtained by fixing the parameter t, and then the integration over time in Equation 27 was performed numerically using adaptive Simpson quadrature at sufficient points r_i of the physical domain in order to obtain a smooth curve. After storing the temperature for each r_i at a fixed t, the graphical solutions were obtained.

The intensity of the heat sources is regarded as constant because in magnetic fluid hyperthermia applications the heat is generated by magnetic relaxational losses in the nanoparticles under the influence of a pseudo-steady magnetic field, i.e. constant frequency and constant amplitude. Under these conditions, the power dissipated by the nanoparticles presents a weak dependence in temperature as depicted by the model developed by Rosensweig [24] for the power dissipation in ferrofluids exposed to alternating magnetic fields. The mathematical formulation of this model is given by the expressionswhere μ₀ is the permeability of free space, χ₀ the magnetic susceptibility, H₀ the magnetic field intensity, f the cyclic frequency, τ the effective relaxation time, φ the volume fraction magnetic particles, M_d the domain magnetisation of a particle, M_s the saturation magnetisation, V_M the magnetic volume, k_b the Boltzmann constant, and T is the temperature.

Considering a ferrofluid composed of monodisperse, single domain magnetite nanoparticles of 12 nm diameter; a concentration of g of magnetite per gram of tissue, which is a normal dosage reported in preclinical and clinical trials [25]; and values for magnetic field intensity and frequency of 6.5 kAm⁻¹ and 500 kHz respectively (in the clinically acceptable threshold [26], [27]), substitution in Equation 28 along with the values for the magnetic properties of magnetite [24] predicts a power of to be dissipated in the tissue.

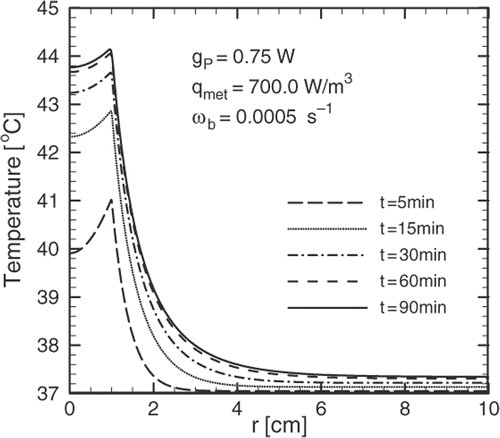
In order to produce the temperature profiles shown in Figure 1 for a shell source of radius , a power dissipation of is needed. From the relationship , where V is the volume of the region where the particles are located, can be deduced that the thickness of the region containing the magnetic nanoparticles must be of the order .

Figure 1. Transient temperature profile for a shell source. Steady state is reached for t ∼ 90 min.

Figure 1 confirms that temperature profiles very close to therapeutic may be obtained if a concentration of approximately of magnetite per gram of tissue is achieved in the surface of the tumour. It can also be seen that there is no significant penetration of the therapeutic temperatures to the outer region. This is due to the small thermal conductivity of the body's tissues. According to Fourier's law, large temperature gradients are needed in combination with the small thermal conductivity of tissues to remove the heat produced by the source. Values for the thermal conductivity of some tissues are listed in Table I [12]. The information in this table validates what was argued in the introduction about the small variations in the thermal conductivities of different tissues. Further, a reference value of k = 0.5 W/m°C was used in this work.

Table I.  Thermal conductivity of some tissues [12].

Tissue	Thermal conductivity (W/m K)
Tumour periphery	0.511
Tumour core	0.561
Colon cancer	0.545
Bone	0.41–0.63
Blood
Pure water	0.627

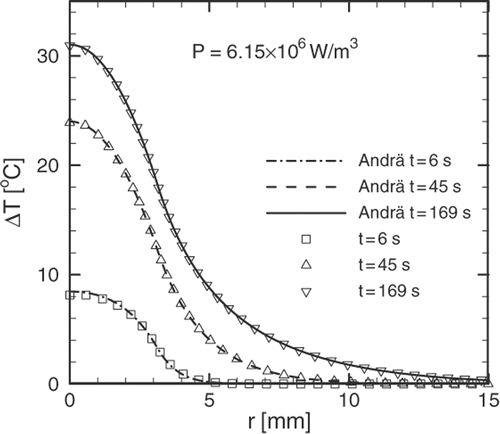
If the transient temperature profiles shown in Figure 1 are compared to those obtained by Andrä et al. [10] for a uniform distribution of the nanoparticles within the tumour, it becomes evident that the superficial distribution presented in this work produces a temperature profile that is closer to the ideal. A relatively uniform distribution can be obtained by direct injection of the magnetic fluid at a low rate [28]. In order to achieve a superficial distribution the ferrofluid must be delivered by arterial embolization with the particles having specific binders at their surface [21].

The solution obtained by Andrä et al. can be obtained from Equation 16 by making ; and using the fundamental solution Equation 15. is the Heaviside unit step function. Figure 2 shows a comparison between the solution presented by Andrä et al. and the solution to the same problem by using the fundamental solution Equation 15 and the GFSE Equation 16. For the purposes of making such a comparison a uniform heat deposition of intensity is confined into a spherical region of radius . This region models a spherical tumour and it is embedded in an unbounded region which models the healthy tissue. The whole domain is regarded as homogeneous having the following thermo-physical properties: .

Figure 2. Agreement between Andrä et al. solution and the solution for the same problem obtained using the fundamental solution (15) and the GSFE (16). A uniform heat generation of intensity is confined in a spherical region of 3.15 mm and a unique value for the thermo-physical properties is used. .

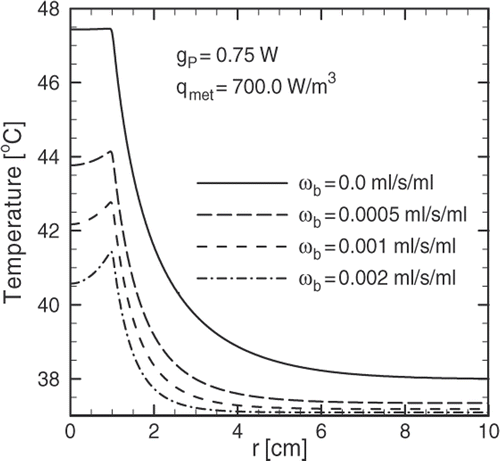
The effect of blood perfusion in the temperature distribution is shown in Figure 3, where the steady state temperature profiles for different values of the blood perfusion coefficient are plotted. In highly vascularised tissues the blood perfusion may be as large as 0.002 mL/s/mL [6] producing temperatures under the therapeutic threshold in the diseased region, potentially affecting the treatment. Instead of a flat profile inside the tumour (ω_b = 0), a decrease in temperature is produced in that region. Also, one must consider that heating causes the thermo-regulating mechanism of the body to increase blood perfusion to keep the temperature at the core body level.

Figure 3. Influence of blood perfusion in the steady-state temperature profile.

The preceding arguments suggest that one must perform a quantification of the blood perfusion coefficient in order to be able to set the values of the magnetic field parameters along with the concentration of magnetic fluid needed to produce therapeutic temperatures for the treatment to succeed. Values for the blood perfusion coefficient for different types of tissues and organs can be found in Diller et al. [12].

The solution to this particular problem showed that heat removal produced by blood perfusion may lead to a temperature profile below the therapeutic threshold. Much of the work that has been done regarding temperature profiles obtained in MFH neglects this effect, potentially leading to incorrect conclusions. A temperature profile close to the therapeutic target can be achieved by concentrating magnetic particles on the tumour surface. This can be obtained by attaching specific binders to the surface of the particles during the synthesis of the ferrofluid. Therapeutic values for the temperature are obtained 20 ∼ 30 minutes after beginning magnetic field application.

The assumption of an infinite domain is valid for deep tissue tumours which are surrounded by healthy tissue. In the case of a relatively superficial tumour a boundary condition modelling the skin-environment interface is needed. In order to solve such a problem, the fundamental solution must be substituted by a Green's function in the GFSE and a term representing the skin boundary must also be included [29]. The method of images provides a way for obtaining Green's functions provided the fundamental solutions are given [30].

Non-symmetrical problems arising due to non-symmetrical tumour shapes or nanoparticle distributions can be solved by means of the boundary element method (BEM) which is a numerical method that uses fundamental solutions as a set of basis functions in its formulation. BEM is based on a discretisation of the surface of the physical domain and then the governing equation is integrated over each element with respect to the basis functions forming the weak formulation of the problem. This process gives rise to a set of linear equations whose solution is the value of the temperature of the nodes of the elements. Then the temperature in any point of the domain is obtained from the nodal temperatures [20]. A way of temperature measuring during hyperthermia treatment could be the development of an algorithm integrating of MR imaging with a BEM code: the particle distribution and the shape of the tumour can be assessed by means of MRI. With the shape of the domain, a boundary element grid can be generated. After inputting the magnetic field parameters along with the magnetic properties of the particles and the thermal properties of the tissue, the solver can be initialised. The output of this computer program may be, for example, a contour plot of temperature.

Although analytical solutions fail when dealing with complex geometries or nonlinearities, they provide the tools for numerical code testing and also for performing a valuable sensitivity analysis of the parameters involved in a problem.

Conclusions

Fundamental free-space Green's functions were developed for the bioheat differential operator in the three principal orthogonal coordinate systems. These are the solution of the differential equation for an unbounded domain such that no particular boundary conditions are imposed on the solution. Their utility for solving bioheat transfer problems was also illustrated. A problem of MFH involving a shell source in the outer region of a solid tumour was formulated and solved by using the fundamental solution in spherical coordinates, demonstrating the application of the solution method presented in this work. A shell heat source is a realistic model distribution that provides an approximately constant therapeutic temperature inside the tumour.

Declaration of interest: This work was supported by the US National Science Foundation (NIRT grant CBET-0609117). The authors report no conflicts of interest. The authors alone are responsible for the content and writing of the paper.

Appendix A: Derivation of the free space Green's function for cylindrical coordinates

Starting fromthe Hankel transform is used, which for an arbitrary function f_(x) is defined as:Here is the Bessel function of the first kind, order zero and argument (λ x). Taking the Hankel transform of Equation A1 yieldsNote that the right hand side of Equation A3 is zero for and , then the solution for those intervals is:Integrating Equation A3 from τ - 0 to τ + 0Recalling that U, and hence , is zero for , so B = 0. Then

AndFinally, taking the inverse Hankel transformThe integral can be integrated analytically:The final expression for U is given bywhere the 2π of the denominator was dropped to be able to present a unique general solution regardless the coordinate system.

Appendix B: Derivation of the free space Green's function for spherical coordinates

Starting fromand performing the transformation , the set of Equations B1–B2 is reduced toTo determine the Green's function associated with Equation B3, the procedure described in Özisik [29] is followed, for which is necessary to consider the homogeneous associated form of the problem, given by:The solution to Equations B5–B6 is readily obtainable from textbooks, e.g. Ozisik [29] or Carslaw and Jaeger [31], it is:It can be demonstrated [32] that the term inside the square brackets is the Green's function at τ = 0 for Equation B3, i.e. , and by replacing t by (t - τ) in Equation B7 then is obtained:The integral can be solved analytically:ThenThe solution of Equations B3–B4 is expressible in terms of the Green's function Equation B10 as:The last step before obtaining the Green's function being sought is to invert the transformation used before Equation B3.Finally, the free space Green's function for Equation B1 is given by the expression inside the curly brackets in Equation B12.

This is the Green's function of the bioheat equation for radial heat flow in an infinite domain in spherical coordinates.