The effect of magnetic nanoparticle dispersion on temperature distribution in a spherical tissue in magnetic fluid hyperthermia using the lattice Boltzmann method

Abstract

In clinical applications of magnetic fluid hyperthermia (MFH) for cancer treatment it is very important to ensure maximum damage to the tumour while protecting the normal tissue. The resultant heating pattern by magnetic nanoparticles (MNPs) in the tumour is closely related to the dispersion of MNPs. In this study the effect of MNPs dispersion on temperature distribution in a tumour and surrounding healthy tissue, during MFH, has been investigated. Accordingly, the Pennes bio-heat equation (BHE) in a spherical tissue with Neumann curved boundary condition has been resolved. The effects of blood perfusion, metabolism heat generation as well as MNPs heat dissipation in an alternating magnetic field as source term, have been considered. To solve the Pennes BHE, the three dimensional lattice Boltzmann method (LBM) has been used. To show the accuracy of the model, simulations have been compared with analytical, experimental and numerical results, reported in the literature. Then, temperature distribution within tissue has been investigated in two cases, homogeneous distribution and Gaussian distribution of specific absorption rate (SAR). Results showed that for the studied cases, unlike homogeneous distribution, Gaussian distribution of SAR is able to raise the temperature of tumour cells above the treatment temperature.

• lattice Boltzmann method
• bio–heat equation
• magnetic fluid hyperthermia
• magnetic nanoparticle dispersion
• SAR

Introduction

Hyperthermia is one of many techniques used in oncology. It uses physical methods to heat certain organs or tissues, delivering an adequate temperature in an appropriate period of time (thermal dose), to the entire tumour volume for achieving optimal therapeutic results. Thermal dose has been identified as one of the most important factors to influence the efficacy of hyperthermia [1]. Although there are definite prescriptions for temperature (generally43°C) and time (usually 60 min), variations in the temperature and the time of delivery are frequent throughout the treatment sessions [1–4].

Hyperthermia is usually used with other forms of cancer therapy, such as radiation therapy and chemotherapy, because hyperthermia will make some cancer cells more sensitive to radiation or harm other cancer cells that radiation cannot damage. The effectiveness of hyperthermia treatment is related to the temperature achieved during the treatment. An ideal hyperthermia treatment should selectively destroy the tumour cells without damaging the surrounding healthy tissue. Hyperthermia can be performed by focusing laser, microwave, ultrasound or magnetic energy to the infected regions. In general, cancer cells possess a higher chance to die when the temperature is above 42.5°C and the rate of death drastically increases with increasing temperature [5–9].

In the past ten years, MFH has drawn greater attention due to the potential advantages for cancer hyperthermia therapy. In MFH, a nanofluid containing the MNPs is injected directly into the tumour. An alternating magnetic field is then applied to the target region, and then MNPs generate heat according to Néel relaxation and Brownian rotation losses as localised heat sources [3], [4], [10]. The heat generated increases the temperature of the tumour. The cancerous cells are then destroyed by raising their temperature to about 42.5°C whereas healthy cells will be safe at this temperature [5], [9].

The temperature that can be achieved in the tissue strongly depends on the properties of the magnetic material used, the frequency and the strength of the applied magnetic field, the blood perfusion in the tissue and the duration of application of the magnetic field. Also the nanofluid injection volume as well as infusion flow rate of the nanofluid are important factors in the concentration of MNPs and SAR within the tissue. Therefore, carefully chosen parameters and the means to monitor the real-time temperature are required [11–14].

In order to kill cancer cells without injury to normal tissues, the ability to predict the temperature distribution inside as well as outside the target region as a function of the exposure time, possesses a high quality of importance. This helps to provide a level of therapeutic temperature and to avoid overheating and dammaging the surrounding healthy tissue [8], [11], [15].

Maenosono and Saita [7] investigated the feasibility of using face-centred cubic iron-platinum (FCC FePt) MNPs for magnetic hyperthermia, as FCC FePt MNPs present a high Curie temperature, high saturation magnetisation, and high chemical stability. To show the heating capability of these MNPs, Maenosono and Saita [7] carried out a theoretical assessment of FCC FePt MNPs as heating elements for hyperthermia by combining the heat generation model and the BHE. Lin and Liu [8] developed a hybrid numerical scheme for solving the transient BHE in spherical co-ordinates. They estimated the temperature rises in biological tissues for the heating effect of FCC FePt MNPs and claimed that the results of Maenosono and Saita [7] are incorrect. Andrä et al. [9] studied MFH and modelled small breast carcinomas surrounded by extended healthy tissue as a solid sphere with constant heat generation. Bagaria and Johnson [11] considered the tissue model as two finite concentric spherical regions with the blood perfusion effect. Tsuda et al. [15] developed an inverse method to optimise the heating conditions during a hyperthermia treatment. Zablotskii et al. [16] studied the heating effect of tuneable arrays of nanoparticles in cancer therapy.

To deliver MNPs to a tumour, two techniques are currently used. The first is to deliver particles to the tumour vasculature through its supplying artery, and the second approach is to directly inject magnetic particles into the extracellular space in tumours [12].

Recently, experiments on magnetic particle diffusion in tissue were performed to study their migration in gel in a steady magnetic field. Salloum et al. [12], evaluated magnetic nanofluid transport and heat distribution in an agarose gel. They used this type of gel because it is claimed to have a porous structure similar to human tissue.

The Pennes BHE model has been widely used among different bio-heat models [17]. This model shows the effect of blood perfusion as a temperature-dependent heat sink term. It is assumed that the blood perfusion effect is homogeneous and isotropic, and that thermal equilibration occurs in the microcirculatory capillary bed. On complication of tissues and their complex geometry, exact solutions aren’t available for many cases. For many practical applications, numerical models such as the finite element method [18–21], finite difference method [22], [23] and Monte Carlo method [24], [25], are widely used nowadays.

To model this problem, LBM may be employed, since this numerical method has been demonstrated to be successful in simulation of fluid flow and heat transfer problems as well as other types of complex physical systems [26–36].

Zhang [37] extended the LBM to solve the Pennes BHE. To our knowledge, it was the first attempt to use LBM to solve bio-heat problems. Huang et al. [38] introduced a thermal curved boundary condition for the doubled-population thermal lattice Boltzmann equation model for uniform regular lattices.

In this work the effect of MNP dispersion on temperature elevation inside tumour and its surrounding healthy tissue has been investigated. Therefore, the Pennes BHE in a spherical tissue with Neumann curved boundary condition has been solved. Moreover, power dissipation of FCC FePt MNPs in an alternating magnetic field as spatial source term in the Pennes BHE has been considered. To solve the Pennes BHE, three dimensional LBM has been used. The estimated results were compared with analytical, experimental and numerical results reported in the literature [8], [12], [39]. To our knowledge, it is the first work using LBM to solve spherical bio-heat problems.

Bio-heat equation

In a generalised form, the Pennes BHE reads:where ρ, c_p and k are the density, the specific heat and the thermal conductivity of the tissue respectively, T is the temperature, t is the time, W_b, p_b, c_ρb and T_b are the perfusion, the density, the specific heat and the temperature of the blood, Q_m and Q_s are the metabolic heat generation of the tissue and the distributed volumetric heat source due to spatial heating.

Equation 1 can be written in a simple form as:where

Thermal lattice Boltzmann method

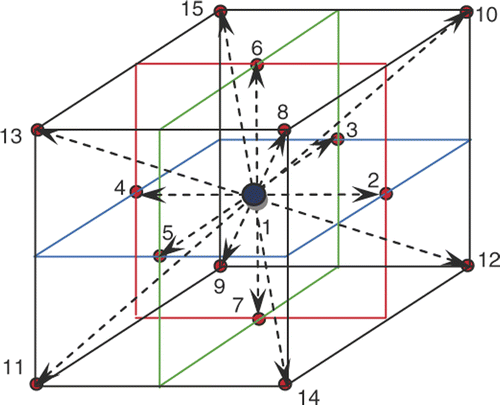
The internal energy evolution equation of the three-dimensional fifteen-speed (D3Q15) LBM is as below [26]:where the distribution function g_i is a set of populations representing the probability of finding a particle at position r at time t moving along the direction identified by the propagation velocity e_i, the subscript i = 1, 2, … , 15 the direction of the thermal population (see Figure 1), Δt is the time step, τ_g is the dimensionless relaxation time, and is the equilibrium distribution of the evolution population g_i,where w_i is the weight factor and equal to 0 for i = 1, 1/9 for i = 2 to 7 and 1/24 for i = 8 to 15 and the propagation velocity is defined as:where C = Δx/Δt is the lattice velocity, and Δx = Δy = Δz are the discrete lattice sizes.

Figure 1. Schematic plot of the D3Q15 lattice.

The dimensionless relaxation time is defined as:where a = k/ρc_p is the thermal diffusivity.

The macroscopic physical quantities can be obtained from the distribution function. For the temperature and heat flux, they are [40], [41]:where W_db is the dimensionless blood perfusion defined as:

Curved boundary condition

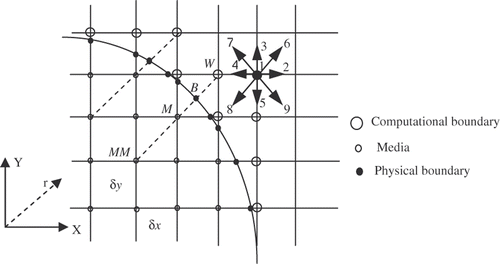
In the curved boundary condition (see Figure 2), to evaluate internal energy density distribution functions, the post-collision distribution function can be obtained as Equation 11 [38]:where is the post-collision distribution function, and are the equilibrium and non-equilibrium part of and  = Δt/( + 0.5Δt).

Figure 2. Curved boundary and lattice nodes (open large circle is computational boundary node, open small circle is media node, filled circle is the physical boundary node in the link of media node and computational boundary).

can be obtained from Equation 5. To determine the , extrapolation method is used. is evaluated as:where Δ is the fraction of the intersected link in the media. According to Figure 2, for calculating the unknown internal energy density distribution functions such as , Δ can be obtained as:

In the Neumann boundary condition, the temperature at the computational boundary nodes (see Figure 2) can be calculated as below:

From Equations 5 and 12 equilibrium and non-equilibrium parts of are obtained to fulfil the collision step [38].

Governing equations

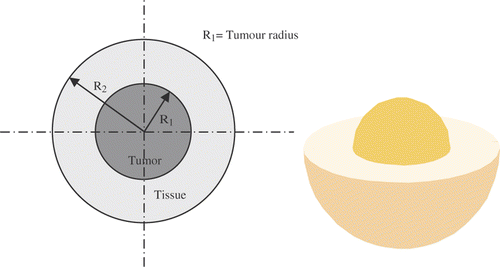
Two concentric spherical regions were chosen as the domain of the analysis with the Neuman boundary conditions (Figure 3). The inner sphere represents the diseased tissue. MNPs are present in the tumour with R₁ radius, that act as sources of heat generation when an alternating magnetic field is applied.

Figure 3. Schematic plot of tissue and tumour. Left, section; right, perspective.

The outer sphere represents the healthy tissue. According to Pennes BHE, Equations 15 and 16 define the transient heat transport in the diseased and healthy tissues, respectively [8]:

In the above equations R₁ and R₂ are tumour radius and healthy tissue radius and subscripts 1, 2, and b are tumour, healthy tissue and blood respectively.

Specific absorption rate

Salloum et al. in their experimental study [12], investigated the magnetic nanofluid transport inside the agarose gel with porosities similar to human tissue. They characterised the SAR distribution in the gel induced by the MNP in an alternative electromagnetic field. Based on their experimental results, they proposed Gaussian distribution for the SAR as:where r is the radial distance from the injection site, r₀ is a parameter (in mm) which determines how far the diffusion occurs, and B determines the maximum strength of the SAR value (W/m³) at the injection site that is power dissipation of MNPs in an alternating magnetic field. The parameter r₀ encompasses the effects of the injection rate and the gel concentration, two important factors that substantially influence the spatial distribution of the nanoparticles. According to Equation 17, higher SAR, measured near the injection site, implies more nanoparticles deposited in the vicinity of the injection site [12].

Power dissipation of MNPs in an alternating magnetic field is expressed as Equation 18 [42], [43]:where μ₀(4π · 10⁻⁷T · m/A) is the permeability of free space, x₀ is the equilibrium susceptibility, H₀ and f are the amplitude and frequency of the alternating magnetic field and τ is the effective relaxation time, given by:where τ_N and τ_B are the Néel relaxation and the Brownian relaxation time, respectively. τ_N and τ_B are written as:where the shorter time constant tends to dominate in determining the effective relaxation time for any given size of particle. τ₀ is the average relaxation time in response to a thermal fluctuation, η is the viscosity of medium, V_H is the hydrodynamic volume of MNPs, k is the Boltzmann constant, 1.38 × 10⁻²³J/K, and T is the temperature. Here, Г = KV_M/kT where K is the magnetocrystalline anisotropy constant and V_M is the volume of MNPs. The MNPs volume V_M and the hydrodynamic volume including the ligand layer V_H are written as:where D is the diameter of MNP and δ is the ligand layer thickness.

The equilibrium susceptibility x₀ is assumed to be the chord susceptibility corresponding to the Langevin equation (), and expressed as:where , , , and φ is the volume fraction of MNPs. Here, M_d and M_s are the domain and saturation magnetisation, respectively. The initial susceptibility is given by:

Generally, the practical range of frequency and amplitudes are often described as 50–1200 kHz and 0–15 kA/m and the typical magnetite dosage is ∼10 mg magnetite MNPs per gram of tumour as reported in clinical studies [4], [44], [45].

In Table 1 the properties of the tissue, the blood, the FCC FePt MNPs and the magnetic field have been shown.

Table 1.  Properties of the tissue, the blood, the FCC FePt MNPs and the magnetic field.

Blood and tissue						FCC FePt MNPs and magnetic field
Property	Unit	Quantity	Property	Unit	Quantity	Property	Unit	Quantity
Qm1	W/m^3	540	ρ1	kg/m^3	1060	ρMNP	kg/m^3	15200
Qm2	W/m^3	540	ρ2	kg/m^3	1060	cpMNP	J/(kg K)	327
Wb1	s^−1	0.0064	cp1	J/(kg K)	3600	Md	kA/m	446
Wb2	s^−1	0.0064	cp2	J/(kg K)	3600	K	kJ/m^3	9
ρb	kg/m^3	1000	Tb	°C	37	δ	nm	1
cpb	J/(kg K)	4180	T0	°C	37	D	nm	9
k1	W/(m K)	0.502	R1	cm	0.5	H0	mT	50
k2	W/(m K)	0.502	R2	cm	1.5	f	kHz	300

Results and discussion

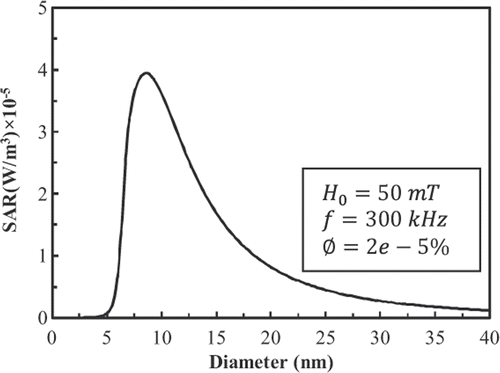
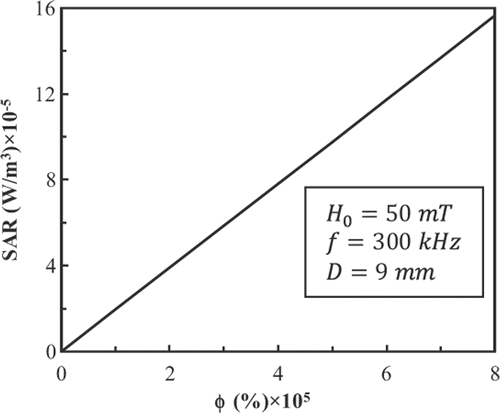
For the LBM simulation, we use 45 × 45 × 45 lattices, therefore R₂ = 19.5 lattice units. Figure 4 shows the power dissipation of FCC FePt MNPs in a magnetic field with fixed amplitude and frequency at 50 mT and 300 kHz and a volume fraction φ = 2 × 10⁻⁵ as a function of particle diameter. Also, Figure 5 shows the power dissipation of 9-nm FCC FePt MNPs in a magnetic field with fixed amplitude and frequency at 50 mT and 300 kHz as a function of volume fraction. There is a linear relationship between power dissipation and volume fraction.

Figure 4. Effect of particle diameter on power dissipation of FCC FePt MNPs.

Figure 5. Effect of volume fraction on power dissipation of 9-nm FCC FePt MNPs.

According to the experimental study of Salloum et al. [39], Pennes BHE in spherical tissue without metabolism with source term equal to SAR can be rearranged as follows:

Note that the temperature field is one-dimensional and only depends on the radial distance from the injection site. Equation 26 can be solved analytically. The following equation gives the steady state temperature distribution in infinite spherical tissue [39]:

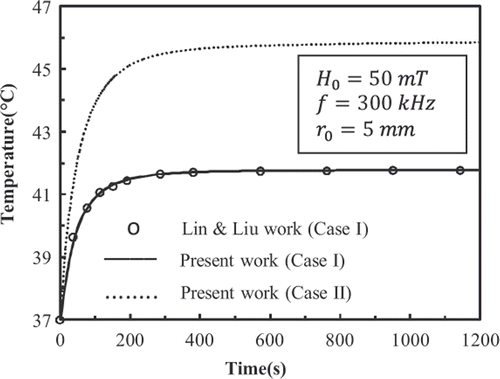
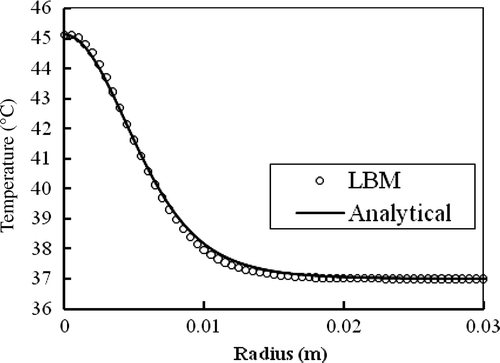
Figure 6 compares numerical and analytical solutions for where B = 800 kW/m³ and r₀ = 5 mm. Agreement is excellent.

Figure 6. Steady state temperature distribution in the infinite spherical tissue for where B = 800 k W/m³ and r₀ = 5 mm.

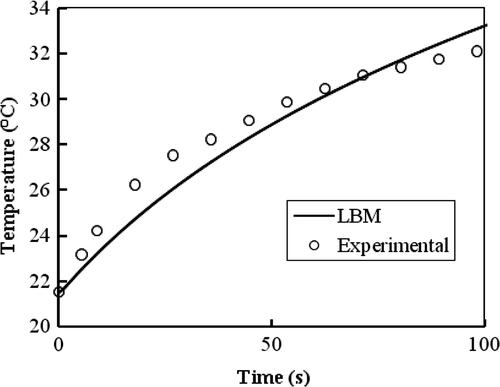
As mentioned, Salloum et al. [12] investigated the diffusion of a nanofluid in the agarose gel possessing porosities similar to human tissue. They examined different gel concentrations as well as different infusion flow rates to identify an idealised injection strategy for achieving a spherical shape of the nanofluid dispersion. They measured the temperature elevations of the injection site in the induced gel by the injected nanoparticles for a gel concentration of 0.2% and an infusion flow rate of 4 µl/min when exposed to an alternating magnetic field as a function of time during 100 s. Figure 7 compares LBM simulation of Pennes BHE in the absence of blood perfusion and metabolism heat generation against the mentioned experimental results.

Figure 7. Temperature elevation in the injection site in agarose gel for a gel concentration of 0.2% and an infusion flow rate 4 µl/min for SAR(r) = Be^−r2/r20 where B = 887.8 k W/m³ and r₀ = 5.62 mm.

Using a numerical scheme, Lin and Liu [8] investigated temperature distribution in the spherical tissue deposited with 9-nm FCC FePt MNPs with volume fraction Ø = 2 × 10⁻⁵, in a magnetic field with fixed amplitude and frequency at 50 mT and 300 kHz. As shown in Figure 4, power dissipation of 9-nm FCC FePt MNPs under mentioned conditions is 3.97 × 10⁵ W/m³. They found that 9-nm FCC FePt MNPs are not able to make the temperature of tumour higher than 42.5°C in the above mentioned conditions.

Salloum et al. [12], in their experimental study, showed that MNP distribution inside tissue is not homogeneous. They proposed a distribution function shown in Equation 17. Accordingly, in this study, temperature distribution within tissue has been investigated in two cases as follows (equal amounts of 9-nm FCC FePt MNPs are used in both cases):

Case I: Homogeneous distribution of SAR

Case II: Gaussian distribution of SAR

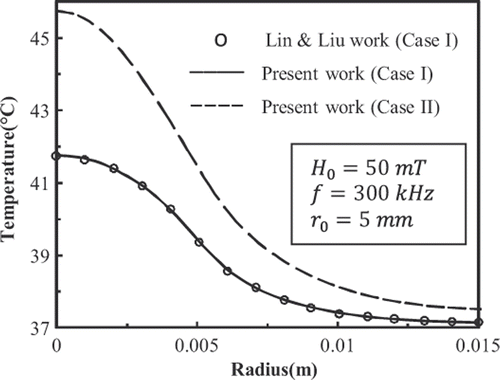
Figure 8 shows the history of temperature at the centre of the tumour deposited with 9-nm FCC FePt MNPs. Figure 9 shows the temperature distributions in the tissue at t = 600 s. In accordance with the results shown in Figure 8, the temperature distribution has become steady at t = 600 s. Figure 10 plots the temperature distributions in the tissue at t = 50 s and t = 100 s.

Figure 8. History of temperature at the centre of the tumour deposited with 9-nm FCC FePt MNPs.

Figure 9. Temperature distributions in the tissue deposited with 9-nm FCC FePt MNPs at t = 600 s.

Figure 10. Temperature distributions in the tissue deposited with 9-nm FCC FePt MNPs at t = 50 s and t = 100 s.

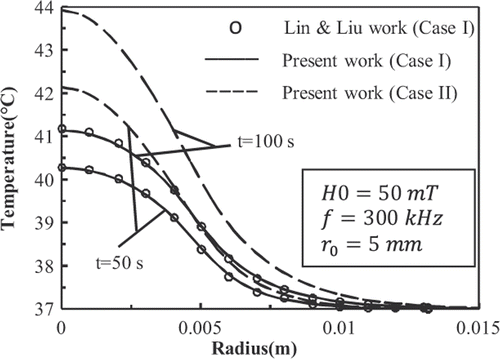
Figures 8–10 show that for case I, the results of present work match well with those given by Lin and Liu [8]. Also it is observed that the Gaussian distribution of SAR in mentioned conditions is able to raise the temperature of the tumour higher than 42.5°C.

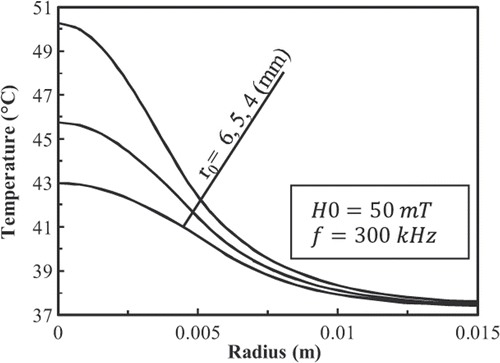
Figure 11 shows the temperature distributions inside the tissue deposited with 9-nm FCC FePt MNPs at t = 600 s as a function of r₀. Results show that reducing r₀ increases the temperature of the tissue.

Figure 11. Temperature distributions in the tissue deposited with 9-nm FCC FePt MNPs at t = 600 s in case II as a function of r₀.

Conclusion

We have extended an LBM for solving the Pennes BHE with thermal curved boundary conditions to predict the temperature distribution inside the spherical tissue in MFH treatment. To show the accuracy of the present work, Lin and Liu's work [8] has been repeated. Results showed that for 2 × 10⁻⁵ volume fraction of 9-nm FCC FePt MNPs, homogenous distribution of SAR cannot raise the temperature of tumours cells above 42.5°C. Moreover, an experimental study [12] investigated the magnetic nanofluid transport in the agarose gel with porosities similar to human tissue. Finally, it proposed the Gaussian distribution for the SAR. Therefore, temperature distribution within the tissue for 2 × 10⁻⁵ volume fraction of 9-nm FCC FePt MNPs for Gaussian distribution of SAR was studied. Results showed that the Gaussian distribution of SAR is able to raise the temperature of tumourous cells above 42.5°C. The results show that the LBM can give precise prediction of the temperature distribution, and it is efficient to deal with the space and time dependent heat source. And, the algorithm is suitable to real-space bioheat problems with curved boundary conditions for practical applications.

Declaration of interest: The authors report no conflicts of interest. The authors alone are responsible for the content and writing of the paper.