3D versus 2D steering in patient anatomies: A comparison using hyperthermia treatment planning

Abstract

Purpose: In this study hyperthermia treatment planning is used to investigate whether the target temperature during hyperthermia treatment can be increased using the 3D AMC-8 instead of the 2D AMC-4 system (AMC: Academic Medical Center).

Methods and materials: The heating ability of the AMC-4 and AMC-8 system was analysed for five patients with cervix uteri carcinoma. Dielectric and thermal models were generated, based on a hyperthermia planning computerised tomography (CT), at a resolution of 2.5 × 2.5 × 5.0 mm³. Calculation of the electric fields with the finite-difference time-domain method was followed by SAR- and temperature-based optimisation. The ability to correct for axial shifts of the patient by phase/amplitude steering was investigated for both systems. Finally, it was investigated whether adjusting the ring-to-ring distance of the AMC-8 system can be used for further optimisation.

Results: An average increase in T₉₀ of ∼0.5°C (0.2°–0.8°C) was found for the AMC-8 system compared to the AMC-4 system. The gain in T₅₀ and T₁₀ was also 0.5°C on average. The additional power required to achieve this gain was 36% to 71% of the power required for the AMC-4 system. The AMC-8 system has the capability of correcting changes in axial position (−8 cm, +8 cm), contrary to the AMC-4 system. For both systems the axial position should be known within 1–2 cm.

Conclusions: Hyperthermia treatment with the AMC-8 system can lead to a clinically relevant increase of the target temperature compared to treatment with the AMC-4 system. The AMC-8 system provides large freedom in the axial positioning of the patient.

• Hyperthermia treatment planning
• physics

Introduction

Hyperthermia has proven its added value when combined with radiotherapy and/or chemotherapy in various randomised phase III trials for different tumour sites [1–3].

These good clinical results were achieved in spite of the fact that the temperature aimed for, 43°C during one hour of treatment, was seldom achieved [4]. The thermal dose administered to the target is generally lower because the potential local overheating of normal tissue prevents applying sufficient power. Increasing the thermal dose is expected to lead to improved clinical results, given that the fraction of tumour cells surviving combined radiotherapy and hyperthermia was found to decrease significantly with increasing target temperature and treatment duration [5].

In most institutes, deep-seated tumours such as cervix uteri carcinoma are heated with loco-regional phased-array systems operating at frequencies in the range of 70–150 MHz [6], [7]. The distribution of the absorbed power can be steered by varying the amplitude and the phase of the electric fields imposed by the individual antennas. In this way the thermal dose delivered to the tumour can be maximised within the limits of patient tolerance.

An important strategy to improve thermal dose delivery during hyperthermia treatment is the use and design of systems with a higher level of control on the power distribution in the patient. The level of control of a loco-regional hyperthermia device is determined by a number of system parameters. Frequency determines the wavelength and thus the scale of the interference pattern. With increasing frequency, electromagnetic waves penetrate with less depth into the patient; at the same time, constructive interference between multiple sources takes place on a smaller spatial scale resulting in a smaller focus as a result of the decreased wavelength. In addition, if the frequency becomes too large, i.e. if the wavelength is much smaller than the typical dimension of the patient, it may no longer be possible to create a single focus.

The number of antennas and their geometric configuration is another important design parameter. Different previous studies [8–11] investigated the effect of antenna number, configuration and applied frequency for different tumour sites on the achieved target temperature or power absorption. In these studies treatment quality was found to improve with an increasing number of antennas organised in multiple rings. The advantage of having a configuration with multiple rings of antennas is that the power or temperature distribution can be steered in 3D whereas a single ring system only allows for steering within a plane.

At our department, loco-regional hyperthermia treatments were carried out using a single ring, four waveguide system operating at 70 MHz: the 2D AMC-4 system [12]. Recently, a new version of the system operating at the same frequency of 70 MHz with an extra ring of four waveguides was introduced in the clinic: the AMC-8 system (Figure 1) [6].

Figure 1. The AMC-8 phased-array 70 MHz waveguide system. The system consists of two rings of four waveguides. Every waveguide has a separate water bolus that provides superficial cooling of the patient and coupling of the incident electromagnetic field into the patient. The two bottom waveguides share the same water bolus. The distance between the two rings is adjustable.

Simulations and measurements in phantoms showed that the full-width half-maximum of the heating pattern was found to be prolonged with at least 50% in the axial direction, depending on the aperture size and the ring-to-ring distance [13]. At equal superficial power deposition, the power in a target located at the centre of the phantom was found to increase when moving from four to eight waveguides with up to 30% [6].

All these pre-implementation studies involved homogeneous phantoms; in this study hyperthermia treatment planning will be used to address the question of whether the target temperature during loco-regional hyperthermia treatment can be increased using the AMC-8 instead of the AMC-4 system. To this end, for both systems, the heating efficacy under standard positioning is investigated as well as its sensitivity with respect to changes in patient position. Furthermore, the ability of both systems to correct for those changes in position by adjustment of phases and amplitudes is investigated. Finally, it is investigated whether the variable ring-to-ring distance provides a useful additional degree of freedom to optimise heating with the AMC-8 system.

Materials and methods

Definition of the patient model

For a group of five patients with a cervix uteri carcinoma, a data-set was acquired with computerised tomography (0.9 × 0.9 × 5.0 mm³) and was automatically segmented into inner-air, fat, bone and muscle tissue, based on the Hounsfield units [14]. The axial extent of the scans was approximately 60 cm. This is not sufficient for simulation of heating with the AMC-8 system and for this reason the scans were extended by copying the top and bottom slices. Appropriate dielectric and thermal parameters were assigned as reported in Table I [15], [16]. A radiation oncologist delineated the gross target volume (GTV) as the target volume for optimisation. Table II gives an overview of a number of patient characteristics.

Table I.  Tissue properties in the electromagnetic and thermal simulations.

Tissue type	σ (S/m)	εr (−)	ρ(kg/m^3)	c (J/(kg K))	k (W/(m K))	Wb (kg/(m^3s))
Inner-air	0.0	1.0	1.29	10000^†	0.024	0
Bone	0.05	10	1595	1420	0.65	0.12
Fat-like	0.06	10	888	2387	0.217	1.1
Muscle-like	0.75	75	1050	3639	0.56	3.6
Tumour	0.74	65	1050	3639	0.56	1.8

Data are taken from Gabriel et al. [15] and the ESHO Taskgroup Committee [16]. σ is the electric conductivity, ε_r the relative electric permittivity, ρ the density of the tissue, c the heat-capacity, k the thermal conductivity and W_b the volumetric tissue perfusion rate.

^†The heat capacity of air is increased by a factor of 10 to allow a larger time step during simulation. The effect on the temperature distribution is negligible.

Table II.  Overview of patient characteristics for the selected patients.

Patient	GTV (cc)	Vfat (cc)	Vmuscle (cc)	DLR (cm)	DAP (cm)
1	139.3	9797	18135	37	24
2	88.9	15417	11048	40	25
3	26.9	17012	12087	38	29
4	52.5	24682	10309	48	26
5	75.1	24042	14245	44	29

V_fat and V_muscle are the volume of fat- and muscle-like tissues respectively. D_LR and D_AP are the largest distance measured for each patient in the left-right and the anterior-posterior direction, respectively.

To reduce the computational costs, the data-set was re-sampled on a 2.5 × 2.5 × 5.0 mm³ grid. The technique used for re-sampling is referred to as the winner-takes-all technique: a low-resolution voxel is assigned the properties of the tissue type that takes up to largest fraction of its volume.

Definition of the phased-array wave guide system and patient positioning

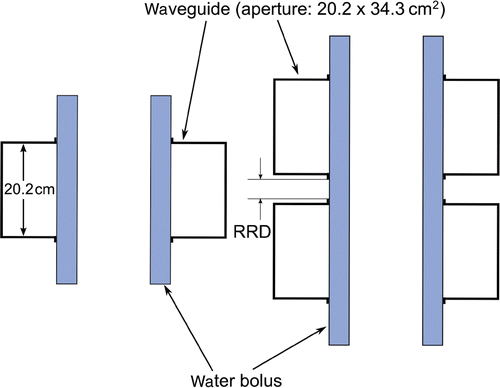
The AMC-4 and AMC-8 system consist of four and eight 70 MHz waveguides (aperture size 20.2 × 34.3 cm²) organised in one and two rings, respectively (Figure 1). Each waveguide can be translated independently in the direction normal to its aperture. In the clinic, the position of the waveguides is chosen such that a gap of 5 cm exists between the waveguides and the patient. Water boluses are placed between these gaps to ensure adequate coupling of the incident electromagnetic field. Furthermore, these water boluses, circulated with distilled water kept at approximately 12°C, provide superficial cooling that is essential to prevent overheating. For the AMC-8 system the distance between the two rings can be varied. Unless mentioned otherwise, this distance was set to 1.5 cm (Figure 2).

Figure 2. Coronal cross-section of the waveguide configuration of the AMC-4 (left) and AMC-8 (right) phased-array system and the water boluses. Waveguide aperture size equals 20.2 × 34.3 cm². The distance between the two rings of the AMC-8 system (ring-to-ring distance (RRD)) can be varied and by default in this study is 1.5 cm.

By default, the patient model was positioned in the AMC-4 model such that the centre of gravity (COG) of the target volume coincides with centre of the applicator ring. For the AMC-8 system, the COG of the target volume coincided with the centre of the two rings. This means that the axial position of the COG is in between the two rings.

Calculation of the electric field distribution

The electric field distribution in the patient was determined by superposition of the fields imposed by the different antennas. Therefore, in the simulations, all waveguides were excited separately with unit amplitude and phase zero to calculate the individual fields.

To compute the electric field distribution, the finite difference time domain (FDTD) method was used [17]. The computational domain was truncated using a perfectly matched layer [18]. By discrete Fourier transformation the complex electric field was stored after 35 000 steps in time (Δt = 0.95 Δt_Courant). To accelerate the FDTD algorithm, a graphical processing unit (GPU) implementation was used [19]. The computation time for a single field was 30–45 minutes for a simulation volume of typically 15 million cells.

Optimisation

To evaluate the performance of the two systems for a series of five patients, two optimisation procedures were followed: SAR- and temperature-based optimisation.

SAR-based optimisation

An optimisation procedure based on the specific absorption rate (SAR) was used to investigate the ability to focus the power absorption on the target region for varying axial positions of the patient for the AMC-8 and AMC-4 system. The patient was shifted in the caudal–cranial direction from −8 cm to +8 cm with 2-cm steps. For each position, the ratio of SAR delivered to the target and delivered to the patient in total was optimised [20]. The optimisation procedure was constrained by requiring that the power delivered by a single antenna is within 10% and 40% and 5% and 25% of the total power for the AMC-4 and the AMC-8 system, respectively.

A drawback of this SAR-based optimisation procedure is that phase and amplitude settings that give optimal coverage of the target region may lead to unacceptably high SAR levels elsewhere. This problem could potentially be solved if there was a rational basis to constrain SAR to specific levels. However, in an (off-line) optimisation procedure, such constraints are hard to define since the corresponding temperature levels are largely dependent on variables such as tissue perfusion and other forms of cooling, e.g. water bolus cooling. Although SAR-based methods can be tailored to suppress overheating with certain efficiency [21], temperature-based optimisation suppresses overheating naturally by setting the maximum tolerable normal tissue temperature as a constraint [22].

Temperature-based optimisation

To investigate the ability of the two systems to heat the target while respecting normal tissue constraints, temperature-based optimisation was performed for varying axial patient positions. As for the SAR-based optimisation, the patient was shifted in a caudal-cranial direction from −8 to +8 cm in 2-cm steps. This shows which patient position leads to optimal heating and, by shifting the patient without changing the phase/amplitude settings, how sensitive the thermal dose is for positioning errors. Das et al. showed, by using Pennes’ bio-heat equation [23], how phase and amplitude can be related to the local temperature T(x, y, z) using the previously calculated electric fields [24]. This method was used in this study. The relevant steady-state temperature fields [24] were calculated using a GPU accelerated finite-difference method. The relevant parameters for the temperature calculations are presented in Table I. We defined the following object function for optimisation [25]:where V_target is the target volume and is a complex valued vector holding the amplitudes and phases of the different sources. This function is minimised under the constraint that the temperature in normal tissue does not exceed a constraint temperature here chosen to be 45°C [26]. The value of T_threshold was set to 43°C. Additional constraints were specified for the contribution to the total power of a single antenna. For the AMC-4 system this contribution should be within 10% and 40%, for the AMC-8 system within 5% and 25%. Solutions to this non-linear constrained optimisation problem were computed using the CFSQP package (eps = 1e-5, epseqn = 1e-5, miter = 35/50 (AMC-4/AMC-8)) [27]. Since the optimisation process might halt on a local minimum, 20 runs with random starting points in phase/amplitude space were performed for the AMC-4 system and 10 runs for the AMC-8 system (to limit the computation time).

In order to determine the potential gain in tumour temperature when treating with the eight-antenna system instead of treating with four antennas, T₉₀, (for 90% of the tumour volume T ≥ T₉₀), T₅₀ and T₁₀ of the target volume were compared. Furthermore the total power absorbed in the patient was calculated. Cumulative temperature–volume histograms (TVH) were made to analyse the differences in the overall temperature distribution.

Variation of the ring-to-ring distance.

Since the distance between the two rings of the AMC-8 system can be varied, it was investigated whether this is a relevant degree of freedom in the optimisation procedure. Hence, temperature-based optimisation was performed setting the ring-to-ring distance to 1.5, 3.5, 5.5 and 7.5 cm. In addition, the sensitivity of the thermal dose to the ring-to-ring distance was investigated. This was done by applying the settings resulting from optimisation at 1.5 cm ring-to-ring distance and evaluating the thermal dose at larger distances.

Results

SAR-based optimisation

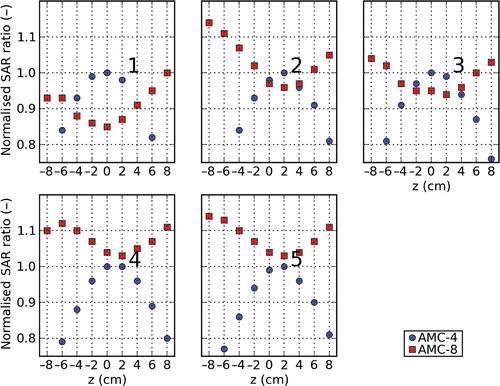
Figure 3 shows the relative SAR ratio (SAR in the target divided by SAR in the total volume) as a function of axial position for both systems for all five patients after optimisation of this ratio. As a scaling factor, the SAR ratio under optimal positioning for the AMC-4 system is used. This figure shows that for the AMC-8 system the SAR ratio increases moving the patient to off-centre positions, whereas for the AMC-4 system the SAR ratio decreases.

Figure 3. The normalised ratio of target- and normal tissue SAR for the AMC-4 and the AMC-8 system for different axial positions after optimisation for patients 1 to 5. The SAR ratios are normalised by the SAR ratio found for the AMC-4 system under optimal positioning. Antennas were not allowed to contribute more to the total delivered power than 40%, or less than 10% for the AMC-4 system, and no more than 25% or less than 5% for the AMC-8 system.

Temperature-based optimisation

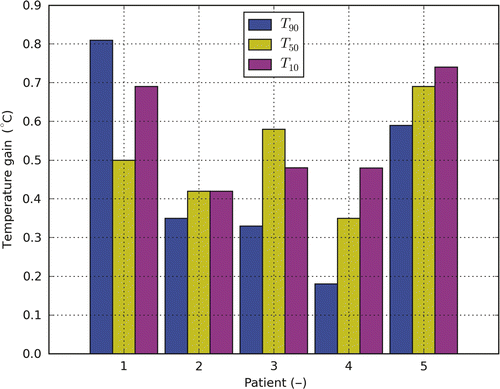
Figure 4 shows the increase in target T₁₀, T₅₀ and T₉₀ for the AMC-8 compared to the AMC-4 system after temperature-based optimisation applying standard positioning. T₉₀ shows an average increase of ∼0.5°C (range 0.2°–0.8°C). T₅₀ and T₁₀ show a similar increase.

Figure 4. The temperature gain for T₁₀, T₅₀ and T₉₀ when moving from the AMC-4 to the AMC-8 system for patients 1 to 5. The applied settings resulted from temperature-based optimisation. For the AMC-8 system a 1.5-cm ring-to-ring distance was applied.

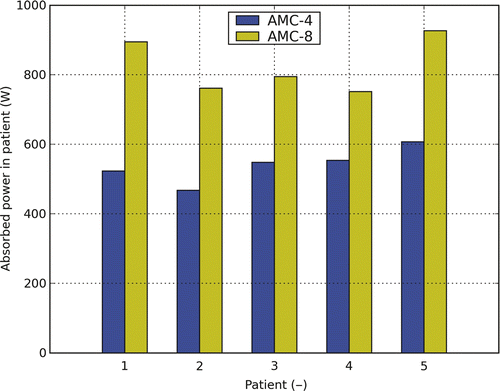
Figure 5 shows the additional power needed to achieve the higher target temperatures for the AMC-8 system. The increase in total power is found to be between 36% and 71% of the power that was required for heating with the AMC-4 system.

Figure 5. Total absorbed power for the AMC-4 and the AMC-8 system for patients 1 to 5. The applied settings result from temperature-based optimisation. For the AMC-8 system a 1.5-cm ring-to-ring distance was applied.

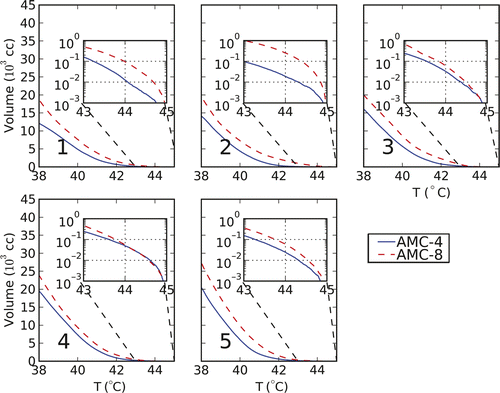
As illustrated in Figure 6, a gain in target temperature is associated with an increase of the volume with a temperature close to the constraint level. As an example, for patient 1 the volume with a temperature of 44°C is ten times larger when treating with the AMC-8 compared to the volume when treating with the AMC-4 system.

Figure 6. Cumulative temperature−volume histograms of the temperature distribution resulting from temperature-based optimisation for the five patients. The inserts zoom in to the 43−45°C range of the histogram. Indicated in the lower left corner of each plot is the patient number.

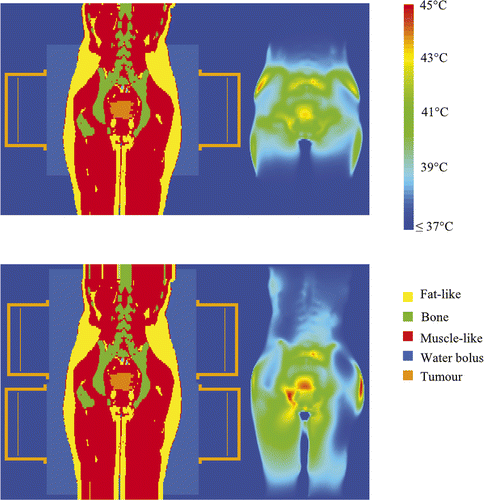
An example of the temperature distribution after temperature-based optimisation for the AMC-4 and the AMC-8 system for one of the five patients (patient 1) is shown in Figure 7. It can be seen that the temperature distribution extends over a larger length in the axial direction (here particularly clear for the legs). Higher tumour temperatures are achieved, however, for the same maximum normal tissue temperature.

Figure 7. An example of the resulting temperature distribution (right) after temperature-based optimisation with the corresponding coronal slices (left) for the AMC-4 system (top) and the AMC-8 system (bottom).

Patient positioning

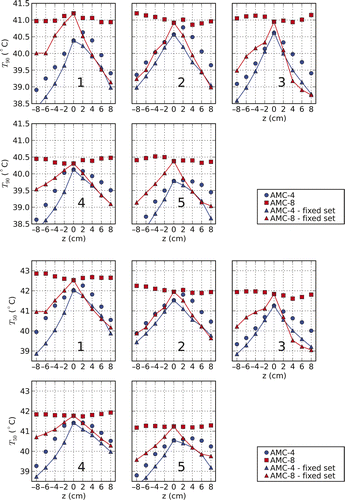
Figure 8 compares the T₉₀ and T₅₀ found using settings from temperature-based optimisation for varying axial patient positions. For every shift T₉₀ and T₅₀ are evaluated using settings that result from I) optimisation with the patient model at the correct/actual position (unconnected markers in Figure 8) and II) optimisation without a shift of the patient (connected markers). It shows the ability of the two systems to correct for axial shifts of the patient. For the AMC-8 system, both the T₉₀ and T₅₀ are found to be relatively stable for all patients over a range of −8 cm to +8 cm. Without correction for axial patient shifts, the thermal dose is found to be equally sensitive for both systems (power was scaled to the highest tolerable level, i.e. such that the maximum temperature equals the constraint temperature). The ability of the AMC-4 system to correct for patient position variations is clearly very limited.

Figure 8. T₉₀ and T₅₀ for different axial shifts (z-axis) of patients 1 to 5. For every shift the T₉₀ and T₅₀ were evaluated for two sets of amplitudes and phases. The first is the result of optimisation with the patient modelled at the correct/actual position (unconnected markers). The second results from optimisation without shifting the patient (connected markers). The figure shows that the AMC-8 system has the capability of correcting for changes in the axial position of the patient, contrary to the AMC-4 system.

Ring-to-ring distance

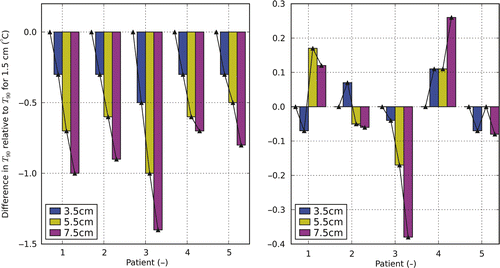
Figure 9 shows the T₉₀ heating with the AMC-8 system using different distances between the two rings relative to the results found using a default 1.5 cm ring-to-ring distance. The left figure shows the effect of increasing the distance without adjustment of phase/amplitude settings (total power is set to the highest tolerable level). Minor deviations (<2 cm) in the ring-to-ring distance led to a decrease of the T₉₀ below 0.3°C (with exception of patient 3). The figure on the right shows the difference in T₉₀ after optimising for 3.5, 5.5 and 7.5 cm distance compared to the T₉₀ found using the ‘standard’ distance of 1.5 cm. The optimal ring-to-ring distance is 5.5 cm for patient 1, 3.5 cm for patient 2, 1.5 cm for patient 3, 7.5 cm for patient 4 and 1.5 cm for patient 5, but in general adjusting the ring-to-ring distance does not lead to a profound improvement in thermal dose delivery.

Figure 9. Differences in T₉₀ after temperature optimisation for the AMC-8 system using varying ring-to-ring distances. Results are relative to the results for a ring-to-ring distance of 1.5 cm. The figure on the left shows the change in T₉₀ applying optimised settings for a 1.5 cm ring-to-ring distance at larger distances without adjustment of settings. The figure on the right shows the T₉₀ optimising for the actual distances relative to the optimal T₉₀ for a ring-to-ring distance of 1.5 cm.

Discussion

This study applied hyperthermia treatment planning to investigate whether the use of the eight antenna, double ring, 3D AMC-8 system is expected to result in higher target temperatures relative to treatment with the single ring, 2D AMC-4 system. A similar comparison is relevant for the 2D BSD Sigma 60 and the 3D BSD Sigma Eye applicator.

Figure 3 showed that the position of the patient in either the AMC-4 or the AMC-8 system plays an important role in the fraction of the total power that can be delivered to the target. This analysis did not take hot-spots into account. Consequently, no statements can be made about the tolerable power level which is to be determined by the maximum temperature in the patient. For the AMC-4 system, moving the patient away from the mid-plane reduces the fraction of power that can be delivered to the target. For the AMC-8 system, moving the patient away from the transversal mid-plane in between the two rings is beneficial for the power delivered to the target. However, superficial levels of power absorption will increase leading to a lower tolerable power level in clinical practice. Different behaviour is expected to occur when comparing the BSD Sigma 60 (2D, 1 ring) and the BSD Sigma Eye applicator (3D, 3 rings). Under standard positioning, in a three ring set-up the target is in the centre of the middle ring, while for the two ring AMC-8 system the target is in between the rings.

Temperature-based optimisation can be constrained more straightforwardly by setting a maximum normal tissue temperature and is therefore preferred over SAR-based optimisation. However, a disadvantage of temperature-based optimisation is the uncertainty in the perfusion distribution under hyperthermic conditions. With the present-day lack of perfusion data, accurate clinical patient-specific temperature-based optimisation is not feasible. The gain found in this study is therefore expected to be dependent on thermal modelling parameters. Our estimates are assumed to represent the correct average but will deviate for the individual patients. However, temperature-based optimisation is clinically the most relevant method to evaluate the heating of the same patient with different apparatus by means of simulation.

Temperature-based optimisation of the target temperature showed an average increase of the target T₉₀ with 0.5°C with large inter-patient variability (0.2°–0.8°C) for the AMC-8 system compared to the AMC-4 system. T₅₀ and T₁₀ increased typically with 0.5°C as well (Figure 4). This increase is clinically relevant since the cumulative minutes at 43°C, a parameter commonly used to describe thermal dose, approximately doubles with every 0.5°C increase in temperature (for temperatures below 42.5°C) [28].

As shown in Figure 8, for the AMC-8 system the tumour temperature expressed as T₉₀ and T₅₀ is relatively insensitive to changes in the axial position of the patient when the optimisation takes the actual position into account. These results are comparable to those of Gellermann et al. for the 3D BSD Sigma Eye applicator [29]. Altering the axial position of the patient might prove to be a strategy to relieve complaints reported in earlier treatment sessions. The absorption at a specific hot-spot can be diminished while the tumour temperature is maintained at the desired level. The impact on the temperature distribution of shifting the patient in the axial direction differs from changing phases and amplitudes. By shifting the patient the electric field distribution of the individual fields is changed while those under phase/amplitude steering obviously remain unchanged. In addition, shifting the patient in the axial direction can be a way to treat patients that under standard positioning have insufficient length to be treated with two rings. The results of Figure 3 and Figure 8 show that positioning accuracy in the axial direction should be within 1–2 cm for both the AMC-4 and AMC-8 system. If this accuracy is achieved, differences in target temperature remain within 0.25°–0.5°C. These are substantial differences compared to the increase in target temperature heating with the AMC-8 instead of the AMC-4 system. Canters et al. [30] found that for the 2D BSD-2000 Sigma 60 system, shifting the patient in the positive z-direction (equivalent to the shifting of the applicator in the negative z-direction) and applying optimised settings for standard positioning reduced the hot-spot–target quotient (HTQ) for which they presented a strong correlation with the target T₅₀. Similar behaviour is not observed in our study since, by optimising directly for temperature, changing the position while not adjusting the settings is expected to make tumour heating less effective. However, it is observed for the AMC-4 system that if the temperature distribution is optimised for varying axial positions, for patients 1, 2, 4 and 5 (Figure 8) a shift in caudal direction of 2 cm (4 cm is optimal for patient 5) causes an increase in T₅₀. This shift corresponds to an applicator shift of 2 cm as discussed in [30].

Figure 9 addresses the question whether the variable ring-to-ring distance (RRD) provides a useful extra degree of freedom in the optimisation of the thermal dose. As the figure illustrates small, patient-specific, differences are found when changing this distance. For patients 1 and 4 relevant improvements were found, while for patients 2, 3 and 5 the standard RRD was either the best choice or improvements were very small (<0.1°C). Given the computational costs associated with including this parameter in the optimisation procedure (those increase with a factor of 4), a standard ring-to-ring distance of 1.5 cm was considered to be acceptable. Moreover, the uncertainties currently present in HTP render it questionable whether relatively small improvements can be predicted accurately for individual patients.

The variable ring-to-ring distance is a unique feature of the AMC-8 system. However, when designing multi-ring systems a choice has to be made for the axial spacing of the antennas as well. Extrapolating our results, in general the impact on heating efficacy will be minor and other requirements such as limiting applicator coupling might have priority.

In our study the patient model is based on the automated segmentation of a CT scan resulting in only a limited number of tissue types. The accuracy of the segmentation in terms of dielectric and thermally alike tissues/tissue types is, however, expected to influence the predicted temperature distribution. However, hot-spots are dominantly located at interfaces of bone, fat, and muscle tissue i.e. high dielectric contrast, in the superficial fat layers (sufficiently deep for cooling to be ineffective), and in the proximity of bony structures due to resonance effects. These hot-spots are expected to dominate the optimisation result. The purpose of our study was to compare two different systems based on patient models that are representative for the population and hence the level of detail used in our study is considered appropriate.

The volume of the patient that is heated with both the AMC-4 as well the AMC-8 system is relatively large compared to the target volume, since these systems are loco-regional hyperthermia devices. The consequences for thermal modelling when large volumes are heated are presently unclear. All thermal modelling done was based on Pennes’ bio-heat equation that is particularly suited for the modelling of small-scale heating problems where arterial pre-heating is expected to be absent. Whether heating of such large volumes can still modelled accurately is unclear. Van den Berg et al. [31] studied the modelling of vascular heat transfer for prostate hyperthermia. They concluded that pre-heating in the arteries feeding the prostate vasculature can be neglected whereas accurate thermal modelling requires including the prostate vasculature. Based on the equilibration length, increasing the heated volume by heating with eight versus four antennas is not expected to cause important differences.

Another effect, not covered in the simulations is the increase in systemic temperature [32]. As shown, a major increase of power is required, and moreover feasible, when heating with eight antennas. As shown in Figure 5, the total power absorbed in the patient to realise the optimised temperature distribution for the AMC-8 system was in the range of 752–927 W as compared to 468–607 W for the AMC-4 system. This is also reflected in Figures 6 and 7, showing that the heated volume is significantly larger for the AMC-8 system. This may result in an extra increase of the systemic temperature that has an important impact on the heat transfer via the vasculature and for example lead to an additional increase in T₉₀. To relate the increase of power to an increase in systemic temperature, further clinical data has to be acquired.

Conclusions

Loco-regional hyperthermia treatment with the 3D AMC-8 system can lead to a clinically relevant increase of the target temperature compared to treatment with the 2D AMC-4 system. The T₉₀ and T₅₀ of the target increased with 0.5°C but with large patient variability. The additional power required to realise this increase ranged from 36% to 71% of the power required for the AMC-4 system. Ring-to-ring distance is of minor importance, but should be known for proper optimisation within 2 cm. For the AMC-8 system, the achievable thermal dose is stable over a range of −8 cm to +8 cm shifting the patient in the caudal–cranial direction. Axial position should be known within 1–2 cm both for the AMC-4 and the AMC-8 system.

Declaration of interest: The work described in this article was financially supported by the Dutch Cancer Society (grant UVA – 2004 – 3834). The authors alone are responsible for the content and writing of the paper.