The electrical conductivity of in vivo human uterine fibroids

Abstract

The purpose of this study was to determine the value of electrical conductivity that can be used for numerical modelling in vivo radiofrequency ablation (RFA) treatments of human uterine fibroids. No experimental electrical conductivity data have previously been reported for human uterine fibroids. In this study electrical data (voltage) from selected in vivo clinical procedures on human uterine fibroids were used to numerically model the treatments. Measured versus calculated power dissipation profiles were compared to determine uterine fibroid electrical conductivity. Numerical simulations were conducted utilising a wide range of values for tissue thermal conductivity, heat capacity and blood perfusion coefficient. The simulations demonstrated that power dissipation was insensitive to the exact values of these parameters for the simulated geometry, treatment duration, and power level. Consequently, it was possible to determine tissue electrical conductivity without precise knowledge of the values for these parameters. Results of this study showed that an electrical conductivity for uterine fibroids of 0.305 S/m at 37°C and a temperature coefficient of 0.2%/°C can be used for modelling Radio Frequency Ablation of human uterine fibroids at a frequency of 460 kHz for temperatures from 37°C to 100°C.

• Thermal ablation
• electrical conductivity
• thermal modelling
• uterine fibroids

Introduction

Radiofrequency ablation is an established technique for the safe and effective local destruction of soft tissue tumours. Technological improvements have made larger and more uniform ablation zones possible, resulting in a broad expansion of RF applications, including cardiac arrhythmias [1], neurological abnormalities [2], [3], and metastatic and/or primary cancer of the liver [4], kidney [5], [6], prostate [7], lung [8], skin [9], and breast [10].

Abdominal myomectomy and hysterectomy are the traditional treatment of symptomatic uterine fibroids. However, over the past decade an increasing demand for safe and effective uterine-sparing treatment options for managing symptomatic uterine fibroids has led to several less invasive procedures. These include laparoscopic and hysteroscopic resection [11], uterine artery embolisation [12], magnetic resonance guided focused ultrasound surgery [13], and medical therapies [14–17]. Most recently, RFA has been used to treat symptomatic uterine fibroids [18–23].

Finite element analysis (FEA) is commonly used to analyse RFA applicator performance to determine tissue temperatures and ablation zone extent. FEA requires specification of all material thermal properties, tissue density, tissue blood perfusion characteristics, and tissue electrical conductivity. Although there are published data for the electrical conductivity of many human tissue types [24–26], the authors were unable to find data for the electrical conductivity of uterine fibroids.

A research study is currently being conducted in the USA and two other countries to demonstrate the safety and effectiveness of radiofrequency ablation for the treatment of patients with symptomatic uterine fibroids [27]. Log entries and digitally recorded electrical data from the procedures were reviewed to isolate those that were suitable for numerical simulation. Most of the treatments had some gas formation along the electrodes of the ablation applicator which precluded them from numerical simulation with finite element techniques. However, three procedures were found to have produced no gas formation and the authors were able to use experimental data from them to determine the electrical conductivity of uterine fibroids. The method and findings are presented in this paper.

Methods

Experimental apparatus

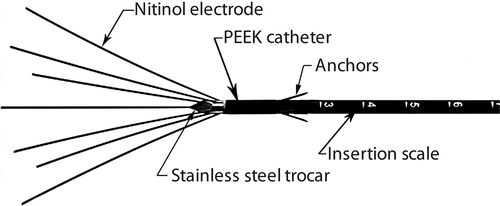
All ablations were conducted with the Halt 2000™ System [27]. This system consists of a radiofrequency generator and accessories (Figures 1 and 2). It is designed to deliver monopolar radiofrequency (RF) energy to tissue through a hand-held disposable electrosurgical RF applicator. The applicator is attached to the control unit and is inserted into a target tissue.

Figure 1. RF Ablation System.

Figure 2. Applicator Detail.

The control unit provides sinusoidally varying voltage at 460 kHz to drive a current through the tissue to be ablated. The current causes resistive heating and the heat then disperses by conduction. During ablations current flows through the applicator, through the body of the patient, through the dispersive electrode pads and returns to the generator. The electrically active portions of the applicator consist of a stainless steel trocar and the deployable electrode array illustrated in Figure 2. The electrodes may or may not be deployed, depending on the size of the fibroid to be treated. Each electrode contains an internal thermocouple embedded 5 mm from the distal end.

The control unit simultaneously samples applied voltage, current and temperatures from the thermocouples that are embedded in the electrodes, and other system parameters. The individual measurements are processed to provide current, voltage, power and temperatures at 50 kHz for internal control purposes and are recorded on an internal hard drive at 1-s intervals. These data were retained as part of the ablation record and were used as the experimentally measured power and voltage data for subsequent analyses.

Heat generated by passing a low frequency RF current through tissue increases proportionally to the square of current intensity. As a result, tissue heating decreases rapidly with increasing distance from the applicator surface. The zone of ablation therefore remains circumscribed to an area close to the applicator which accounts for the controllable ablation zone size that is characteristic of RF ablation.

The ablation system has two modes of operation. The most common operational mode is to set an average electrode target temperature, as measured by the embedded thermocouples. The internal control system continuously adjusts the applied voltage to achieve the specified average target temperature. This mode is only used with the electrodes extended and the target temperature typically ranges from 95°C–100°C. This produces an ablation zone surrounding the electrodes and trocar. The size of the ablation zone depends on the tissue temperature and duration of exposure [28].

For the second mode of operation the electrodes are not deployed. This mode is employed when the fibroid is too small to extend the electrodes and contain all the active heating surfaces within the fibroid being treated. Since the electrodes are not extended, the embedded thermocouples cannot be used to control applied voltage. For this mode, the total power is set at a target value and the system controls the applied voltage to maintain the target power. There are no near tissue applicator temperature measurements made during this mode of operation.

Human in vivo ablation treatments

The in vivo ablation treatments were part of a study to demonstrate the safety and effectiveness of radiofrequency ablation (RFA) for the treatment of patients with symptomatic uterine fibroids [29]. Most of the ablations were conducted with the electrodes deployed and at electrode temperatures that resulted in some gas formation adjacent to the electrodes. As pointed out by Chang [30], gas generation is commonly seen in the clinical use of radiofrequency ablation. However, this study is limited to single phase ablation in order to facilitate numerical simulation, so data from all ablations that resulted in gas formation were excluded from consideration.

Several in vivo ablations were performed where the subject was to obtain a hysterectomy. These tests were referred to as peri-hysterectomy tests. All tissue excised at the time of this subsequent surgery underwent a pathology assessment. The electrical data from these peri-hysterectomy studies were not suitable for electrical conductivity evaluation because the electrode temperatures resulted in gas formation. However, the pathology reports yielded information on ablation zone shape and location and further confirmed that the entire active portion of the applicator was within the fibroid being treated when indicated by ultrasound visualisation.

As part of the research study protocol, the entire active portion of the applicator, including any extended electrodes, has to be completely within the fibroid being treated. In order to comply with this protocol requirement three of the ablations were conducted with the electrodes completely retracted. These ablations were done at a power of 15 W and there was no indication of gas generation from the ultrasound visualisations. Subsequent numerical modelling of these ablations also indicated that no boiling took place. The applicator voltage and power data from these three ablations were subsequently used with the numerical model to simulate the procedures.

Numerical analyses

Tissue temperatures were calculated using a commercially available finite element code (COMSOL Version 3.5a, Comsol, Burlington, MA).

Governing relationships

The RF ablation device operates at a frequency of 460 kHz. At this relatively low frequency, and with no internal sources of electric current, the electric field is described by Laplace's equation:where ∇ is the vector gradient operator, V is the electric potential (Volts), and σ (T) is the electrical conductivity (Siemens/meter).

Temperature is calculated using the modified Penne's bioheat equation [31]:in which ρ is the tissue density (kg/m³), C is the heat capacity of the tissue (J/kg-K), Tis the local tissue temperature (°C), k is the thermal conductivity of the tissue (W/K-m), σ and V are the tissue electrical conductivity and electric potential defined above. Q_m is the metabolic heat source term (W/m³) which is assumed insignificant for the present case, ρ_b is blood density (kg/m³), C_b is the heat capacity of blood (J/kg-K), ω is the blood perfusion coefficient (1/sec), and T_amb is the ambient body temperature as carried by the blood through the body (°C). The term is referred to as the blood perfusion term.

Material properties

The following values (Tables I–III) were used for material properties:

Table I.  Human uterus.

Parameter	Symbol	Value	Units	Reference
Electrical conductivity	σ	To be determined	S/m	–
Density	ρ	1052	kg/m^3	[32], p. 139]
Thermal conductivity	k@37°C	0.512^a	W/K-m	–
Heat capacity	C	3600^b	J/kg-K	–
Blood density	ρb	1055	kg/m^3	[32], p. 138]
Blood heat capacity	Cb	3840	J/kg-K	[32], p. 28]
Blood temperature	Tb	37	°C	–
Perfusion coefficient	ω	0.0064	1/sec	^c

^aThis value is within the range reported in [32], pp. 14–15 for human muscle and human liver.

^bTaken to be the same as human liver reported in [32], p 28. This value is also approximately the same as that reported [32], p 28 for human muscle. As discussed later, the exact value for tissue heat capacity has a negligible effect on the calculated power.

^cA wide range of blood perfusion rates are reported for tissue. As discussed later, the value for perfusion has a negligible effect on the calculated power for the conditions of this study.

Table II.  Catheter (PEEK – Victrex 381 G).

Parameter	Value	Reference
ρ	1300	33
k	0.25	33
C	2160	33

Table III.  Trocar (304 Stainless Steel).

Parameter	Value	Reference
ρ	8000	33
k	16.2	33
C	500	33

The effect of temperature on tissue thermal conductivity is accounted for by the relationship shown in Equation 3. This relationship utilises the previously cited tissue thermal conductivity at 37°C and a linear temperature coefficient which is the average of those shown by Duck [32], p. 18], for human cardiac muscle (0.0024), human liver (0.0025), and human spleen (0.0026).The final parameter required to numerically model the clinical procedures is the tissue electrical conductivity.

Initial examination of the clinical data suggested that the tissue electrical conductivity increases slightly with increasing temperature. Also, a linear change in conductivity with temperature for some animal tissue has been reported by Duck [32], p. 173].

Based on these observations, Equation 4 was utilised to model electrical conductivity:where α is the temperature coefficient.

Clinical power simulations

As previously mentioned, three clinical procedures were done with the electrodes completely retracted. These three clinical procedures were numerically simulated. The numerical designations for these procedures are 503, 504, and 505.

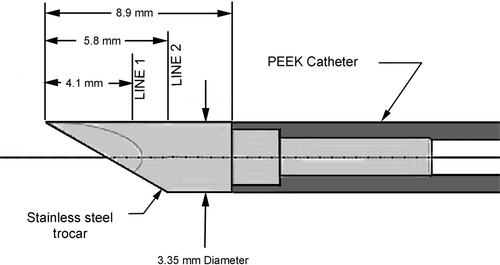
Figure 3 is a view of the RF applicator with the electrodes completely retracted. This figure also depicts the two lines, Line 1 and Line 2, where computed tissue temperature profiles are subsequently presented. All treatments and simulations were performed with the configuration of Figure 3.

Figure 3. Side view of trocar showing line locations for tissue temperature profiles.

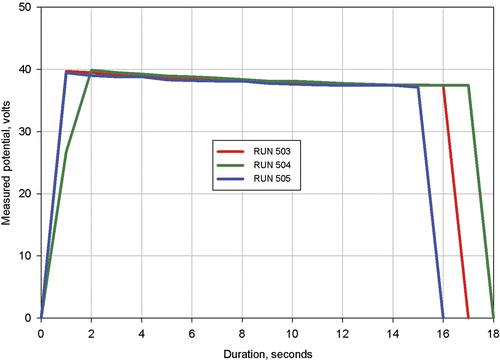
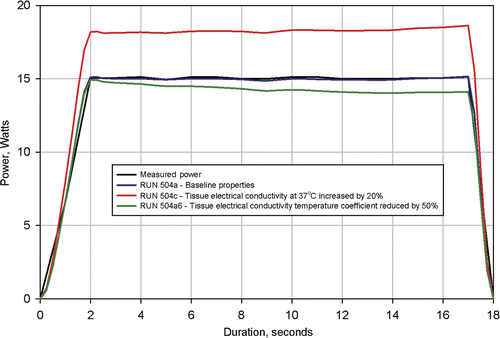
The measured applied voltages for procedures 503, 504, and 505 are shown in Figure 4. This figure shows that after two seconds, the applied voltage profiles were nearly identical for the three procedures. It is difficult to exactly compare applied voltages at the same durations because the voltage values were recorded only every second, so there was insufficient resolution in recording time to define the start of heating or the exact voltage profile during the initial 1 or 2 s of heating. However, it is clearly seen that the applicator voltage profiles required to maintain a constant power of 15 W decayed at approximately the same rate for each procedure. Since the near electrode tissue temperature increases during treatment, this decay indicates that the tissue electrical conductivity increases with increasing temperature. Subsequent simulations of the procedures confirmed this expected result.

Figure 4. Measured applied voltage for Procedures 503, 504, and 505.

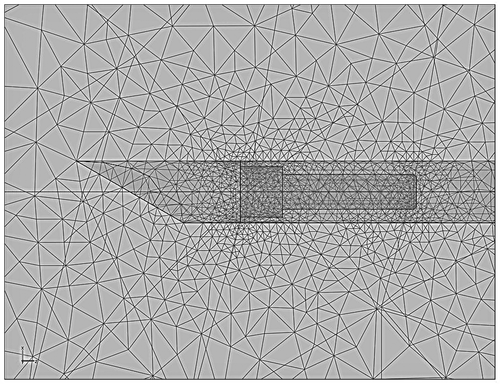
The trocar and tissue were meshed with approximately 10,000 elements. As an experiment, the numerical model was also meshed with approximately 100,000 elements to see if the finer mesh would result in any substitute effect on calculated power or temperature values. The effect on calculated values was found to be negligible. The mesh is shown in Figure 5 viewing through the plane of symmetry for the 100,000 element simulation.

Figure 5. Side view of trocarshowing mesh for a simulation utilizing approximately 100,000 elements.

During this study procedures 503, 504, and 505 were numerically simulated to determine the values for electrical conductivity at 37°C, σ_@37°C, and linear temperature coefficient, α, that would result in the simulated power dissipation profile matching the experimentally measured profiles. For all simulations the values of σ_@37°C and α were specified by the use of Equation 4.

Results

Figures 6–8 show the measured power dissipations and the power dissipations computed from numerical simulations of procedures 503, 504, and 505. In each numerical simulation values for tissue conductivity at 37°C and linear temperature coefficient were utilised that resulted in agreement between measured and calculated power dissipations. Several simulations had to be made for each procedure to determine the required tissue conductivity at 37°C and the required linear temperature coefficient.

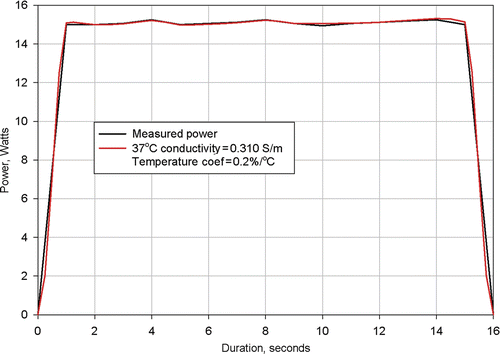
Figure 6. Results from simulation of Clinical Ablation 503 showing measured power dissipation and computed power dissipation with a 37°C tissue electrical conductivity of 0.305 S/m and a tissue electrical conductivity temperature coefficient of 0.2%/°C. Electrodes completely retracted.

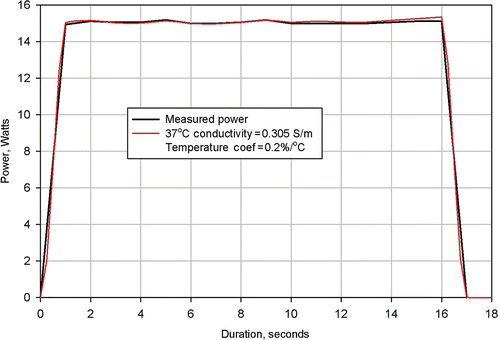
Figure 7. Results from simulation of Clinical Ablation 504 showing measured power dissipation and computed power dissipation with a 37°C tissue electrical conductivity of 0.300 S/m and a tissue electrical conductivity temperature coefficient of 0.2%/°C. Electrodes completely retracted.

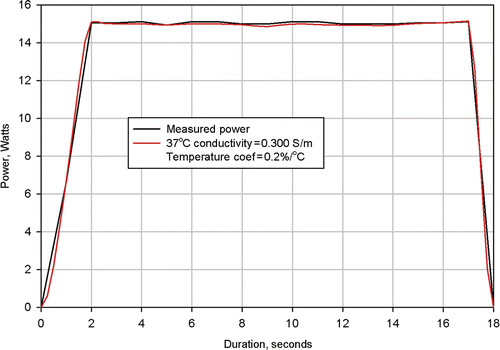
Figure 8. Results from simulation of Clinical Ablation 505 showing measured power dissipation and computed power dissipation with a 37°C tissue electrical conductivity of 0.310 S/m and a tissue electrical conductivity temperature coefficient of 0.2%/°C. Electrodes completely retracted.

The task was simplified because, at start of heating, the tissue temperature was nearly 37°C throughout and the value used for linear temperature coefficient had minimal effect on computed initial power dissipation. Consequently, it required only a few simulations with an assumed value of α to converge on a value for σ_@37°C that resulted in an early time power dissipation of 15 W.

Once this initial value was obtained, simulations were made using it to determine the value of α that would result in the power dissipation remaining constant. The process for determining σ_@37°C was then repeated using the refined value for α. The process had to be repeated only once to arrive at the final values for σ_@37°C and α.

Figure 6 shows the measured power dissipation from Procedure 503 and the power distribution calculated from a numerical simulation of the same procedure. As can be seen, agreement between the two curves is excellent. This agreement was achieved using a value of 0.305 S/m for the 37°C value of tissue conductivity and a value of 0.2%/°C for the tissue temperature coefficient.

Figure 7 shows the measured power dissipation from Procedure 504 and the power distribution calculated from a numerical simulation of the same procedure. Again, agreement between the two curves is excellent. However, for this procedure, it was necessary to utilise a value of 0.3 S/m for the 37°C tissue conductivity and a value of 0.2%/°C for the tissue temperature coefficient.

Figure 8 shows the measured and computed power dissipations for procedure 505. In this numerical simulation it was necessary to utilise a value of 0.31 S/m for the 37°C tissue conductivity and a value of 0.2%/°C for the tissue temperature coefficient.

In Figures 6–8, values of 0.305 S/m, 0.3 S/m, and 0.31 S/m respectively for the 37°C value of conductivity resulted in the simulated power profiles matching the measured power profiles. In all cases the utilised temperature coefficient was 0.2%/°C.

The average electrical conductivity value of 0.305 S/m has a standard deviation of 0.005 S/m.

The temperature coefficient, α, had a positive value, which was expected from the previous examination of the applied voltages shown in Figure 4.

The numerical simulations shown in Figures 6–8 were done utilising the material thermal properties previously listed. Since the thermal properties of uterine fibroids are not known and were estimated based on a different human tissue, it was necessary to evaluate the effect that this uncertainty had on calculated power.

This evaluation was performed by performing simulations of each procedure with different values for tissue thermal conductivity, tissue specific heat capacity, tissue perfusion coefficient, and trocar conductivity. The results were the same for each set of simulations and the results shown in Figure 9 from procedure 504 are representative of those from procedures 503 and 505.

Figure 9. Results from simulation of Clinical Ablation 504 showing measured power dissipation and computed power dissipation with a 37°C tissue electrical conductivity of 0.300 S/m and a tissue electrical conductivity temperature coefficient of 0.2%/°C (baseline conditions). Electrodes completely retracted. Four additional simulations shown with tissue thermal conductivity increased by 20%, tissue heat capacity increased by 20%, trocar thermal capacity increased by 5%, and perfusion coefficient changed from 0 to 6.4e-3 1/s.

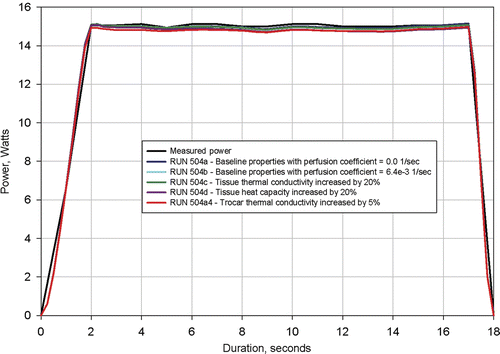
Figure 9 shows that a plus and minus 20% change in tissue thermal conductivity and specific heat has negligible effect on calculated power. The figure also shows that a large change in perfusion coefficient and a 5% change in trocar thermal conductivity have a negligible effect on calculated power.

The result that exact values for utilised tissue thermal properties have a negligible effect on the computed power dissipation is a crucial finding of this study because it permits the extraction of electrical conductivity when the thermal properties are not precisely known.

Figure 10 was produced to demonstrate the sensitivity of computed power dissipation to the utilised value of electrical conductivity. In this figure the power dissipation profiles for the three procedures were computed with the 37°C conductivity increased by 20% and with the temperature coefficient reduced by 50%. Again, the results were the same for each set of simulations and the results shown in Figure 10 from procedure 504 are representative of those from procedures 503 and 505. Results of these calculations, shown in Figure 10, demonstrate that calculated power dissipation is sufficiently sensitive to utilised tissue electrical conductivity to permit the determination method employed here.

Figure 10. Results from simulation of Clinical Ablation 504 showing measured power dissipation and computed power dissipation with a 37°C tissue electrical conductivity of 0.300 S/m and a tissue electrical conductivity temperature coefficient of 0.2%/°C (baseline conditions). Electrodes completely retracted. Two additional simulations shown with tissue electrical conductivity at 37°C increased by 20% and tissue electrical conductivity temperature coefficient reduced by 50%.

Finally, in order to determine the tissue temperature range for which the electrical conductivity was determined, tissue temperatures were extracted from the simulation results. Temperature profiles were plotted on Figures 11 and 12 for three times: 8 s, 12 s, and 16 s along two radial lines from the trocar, Line 1 and Line 2. The locations of these lines are shown on Figure 3.

Figure 11. Computed tissue temperatures outward on a radius from the trocar surface at a distance of 4.1 mm from the trocar tip. The temperature profiles are shown at durations of 8 seconds, 12 seconds, and 16 seconds. Profiles are shown with the nominal value for tissue thermal conductivity and the nominal value increased by 20%.

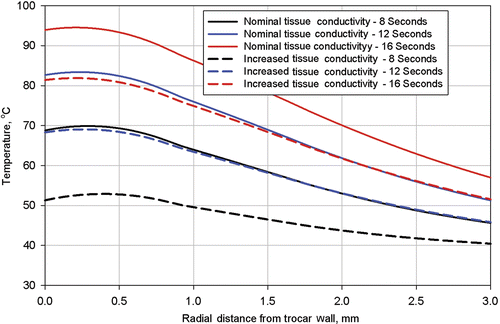
Figure 12. Computed tissue temperatures outward on a radius from the trocar surface at a distance of 5.8 mm from the trocar tip. The temperature profiles are shown at durations of 8 seconds, 12 seconds, and 16 seconds. Profiles are shown with the nominal value for tissue thermal conductivity and the nominal value increased by 20%.

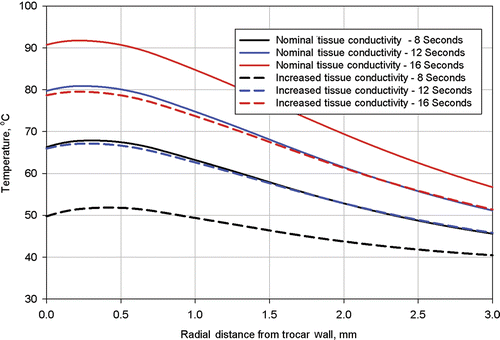
Each figure has plots for two different values of tissue thermal conductivity, the nominal value used for the simulation of procedure 504 and the nominal value increased by 20%. Results of these calculations are shown in Figure 11 for Line 1 and Figure 12 for Line 2.

Discussion

Results of the simulations shown in Figures 6–8 yielded an average electrical conductivity for uterine fibroids of 0.305 S/m at 37°C and a temperature coefficient of 0.2 %/°C with a standard deviation of 0.005 S/m for the conductivity at 37°C. It is the authors’ opinion that this amount of variation is characteristic of that seen in tissue electrical conductivity measurements.

The temperature coefficient of 0.2%/°C results in a maximum computed conductivity change of 12.5% for a 60°C increase in tissue temperature. As a result of this low value for the temperature coefficient, it was not possible to detect any non-linearity in the effect of temperature on conductivity. Consequently, the linear relationship of Equation 4 used to describe the effect of temperature on electrical conductivity was appropriate for this study.

The simulations shown in Figure 9 demonstrated that the values determined for tissue electrical conductivity were insensitive to the exact values of tissue thermal conductivity, heat capacity, and blood perfusion coefficient for the simulated RF applicator geometry, treatment duration, and power level. As previously mentioned, this was a crucial finding because it demonstrated that tissue electrical conductivity could be determined without precise knowledge of the values of these parameters.

Tissue thermal properties will have a significant effect on the temperature distribution in the tissue and size of the ablation zone [30]. However, the present study was directed specifically to extracting electrical conductivity. Ablation zone size could not be obtained because the electrical data were obtained from in vivo clinical treatments from which the fibroids were not harvested for examination.

The simulations shown in Figure 10 with changes in electrical conductivity and temperature coefficient provide an indication of the sensitivity of the utilised method for determining electrical conductivity. Based on Figure 10 the authors believe that the values reported for conductivity are adequate for numerical simulations.

The near applicator temperatures shown in Figure 11 are slightly higher than those shown in Figure 12 because Line 1 is closer to the trocar tip, where temperatures are higher. In all cases, the near applicator temperatures with higher tissue thermal conductivity are lower than with the nominal thermal conductivity because energy is better conducted away from the zone of highest volumetric heat generation. Also, temperatures at the applicator (trocar) surface are slightly lower than those approximately 0.25 mm from the applicator surface because of the heat transfer to the relatively cool stainless steel trocar. This calculated temperature dip at the applicator surface would not necessarily occur at different (higher) power levels and to smaller applicators with less thermal conduction capability and less thermal heat capacity (i.e., the nitinol electrodes).

The method for conductivity determination used in this study requires that the treatment procedure records include all ablation system parameters, particularly the current, voltage and power readings. Secondly, it is the authors’ opinion that the RF applicator configuration must be simple enough so that it can be very accurately simulated. For example, long extended electrodes are often subject to deflection in a non-predictable manner which would preclude sufficiently accurate modelling of the RF applicator for determination of tissue conductivity. Also, because of limitations in accepted numerical simulation methods for tissue, tissue temperatures must be low enough to preclude gas formation during treatment. These conditions were met for the three procedures that were analysed.

Conclusions

Power dissipation profiles measured during three in vivo clinical ablations of uterine fibroids were compared with the power profiles computed from numerically modelling the same procedures. These comparisons showed that an electrical conductivity for uterine fibroids of 0.305 S/m at 37°C and a temperature coefficient of 0.2 %/°C can be used for modelling radio frequency ablation of human uterine fibroids for temperatures from 37°C to 100°C.

The comparisons also showed that the use of a linear temperature dependency adequately simulates the effect of temperature on the electrical conductivity of uterine fibroids for the temperature range simulated.

Declaration of interest: The authors report no conflicts of interest. The authors alone are responsible for the content and writing of the paper.