Improved power steering with double and triple ring waveguide systems: The impact of the operating frequency

Abstract

Introduction: Regional hyperthermia systems with 3D power steering have been introduced to improve tumour temperatures. The 3D 70-MHz AMC-8 system has two rings of four waveguides. The aim of this study is to evaluate whether T₉₀ will improve by using a higher operating frequency and whether further improvement is possible by adding a third ring.

Methods: Optimised specific absorption rate (SAR) distributions were evaluated for a centrally located target in tissue-equivalent phantoms, and temperature optimisation was performed for five cervical carcinoma patients with constraints to normal tissue temperatures. The resulting T₉₀ and the thermal iso-effect dose (i.e. the number of equivalent min at 43°C) were evaluated and compared to the 2D 70-MHz AMC-4 system with a single ring of four waveguides. FDTD simulations were performed at 2.5 × 2.5 × 5 mm³ resolution. The applied frequencies were 70, 100, 120, 130, 140 and 150 MHz.

Results: Optimised SAR distributions in phantoms showed an optimal SAR distribution at 140 MHz. For the patient simulations, an optimal increase in T₉₀ was observed at 130 MHz. For a two-ring system at 70 MHz the gain in T₉₀ was about 0.5°C compared to the AMC-4 system, averaged over the five patients. At 130 MHz the average gain in T₉₀ was ∼1.5°C and ∼2°C for a two and three-ring system, respectively. This implies an improvement of the thermal iso-effect dose with a factor ∼12 and ∼30, respectively.

Conclusion: Simulations showed that a 130-MHz two-ring waveguide system yields significantly higher tumour temperatures compared to 70-MHz single-ring and double-ring waveguide systems. Temperatures were further improved with a 130-MHz triple-ring system.

• Hyperthermia
• RF heating, waveguides
• hyperthermia treatment planning
• thermal dose

Introduction

In clinical hyperthermia a tumour temperature of 43°C for 1 h is pursued [1], but this goal temperature is rarely achieved. Adding hyperthermia to radiotherapy or chemotherapy improves clinical outcome [2–5], but in view of the dose effect relation observed both in vitro and in vivo [6–9], results can be further improved when higher tumour temperatures could be realised without overheating normal tissue.

Locoregional hyperthermia of deep-seated tumours is generally performed with phased array systems operating at 70–140 MHz. Systems with 2D power steering have been widely used for many years [10], [11]. The commercially available BSD Sigma-60 applicator (BSD Medical Corporation, Salt Lake City) operates at a variable frequency between 60 and 120 MHz and consists of 8 paired dipoles in a single ring [11]. The Academic Medical Center (AMC) in Amsterdam has many years of experience in locoregional hyperthermia treatments with the 70-MHz AMC-4 system, which consists of a single ring with four waveguides [10]. Aiming for a tumour temperature of 43°C, normal tissue hot spots are difficult to avoid with these limiting 2D steering possibilities. Therefore, applicator systems with antennas arranged in multiple rings have been introduced in the clinic to provide 3D power steering [12–15]. An upgrade of the 2D BSD Sigma-60 is the 3D Sigma-Eye [12], which consists of three rings of eight paired dipole antennas and operates at a fixed frequency of 100 MHz. At the AMC, the 3D 70-MHz AMC-8 system has been developed and built [13], consisting of two rings of four waveguides, identical to those of the 2D AMC-4 system. The distance between the two rings can be adjusted and it is also possible to use the AMC-8 system as a single-ring system when the occasion arises. The increased number of degrees of freedom of these 3D systems makes it possible to realise higher tumour temperatures, since it provides better spatial power steering, thereby reducing the incidence of normal tissue hot spots.

The improvement in heating capabilities of new system designs needs to be investigated. Hyperthermia treatment planning is a very useful instrument to obtain insight into the heating capabilities of different systems and antenna configurations [14–18]. The antennas and water boluses of the AMC-8 system cover a large part of the patient's body as the waveguides are identical to those of the AMC-4 system. During the first clinical experience with the AMC-8 system this was found to be less ideal for short patients. A simulation study investigated the impact of smaller waveguide apertures on the heating capability of the AMC-8 system [17]. It was observed that the tumour temperatures that could be realised with aperture sizes in the range of 20.5 × 34.25 cm² to 8.5 × 34.25 cm² were comparable. This suggests that a 70-MHz double-ring system with aperture sizes of 8.5 × 34.25 cm² is a proper system design for clinical hyperthermia which can also be used to treat short patients.

Simulation studies by Kroeze et al. and Seebass et al. [14], [15] demonstrated a favourable effect of higher operating frequencies for systems with multiple antenna rings. Kroeze et al. proposed a 150-MHz regional hyperthermia cavity slot (RHOCS) applicator, consisting of three rings of six antennas. This allowed a SAR increase in the tumour of 1.7 relative to the 70-MHz coaxial TEM applicator [15]. Seebass et al. varied the number of rings (one, two or three rings), the number of dipoles per ring and the frequency (100, 150 or 200 MHz) and found an optimal configuration for a three-ring 150-MHz applicator with either eight dipoles or six paired dipoles per ring. An advantage of a higher frequency is that the smaller wavelength of the electromagnetic waves allows steering on a smaller scale. This should help to reduce hot spots in normal tissue. Van der Wal et al. [19] showed, for example, that hot spots in the lower back or on the sides can be reduced by increasing the frequency of the BSD Sigma-60 applicator. On the other hand, the penetration depth decreases with increasing frequency, which can be a disadvantage for the power administered to the deep-seated tumour. The type of antennas, their number and geometrical arrangement will have an impact on the locations where normal tissue hot spots occur [16], [20] and the temperature level that can be achieved in the tumour is dependent on the temperature at the hot spot locations. Therefore, whether a higher operating frequency is favourable also depends on the type of antennas and the antenna arrangement as well as the number of rings, and results and conclusions from the aforementioned studies with dipole or cavity slot antennas cannot be extrapolated directly to heating systems with rectangular waveguides.

The goal of this study is to determine the optimal frequency and number of rings for a locoregional hyperthermia phased array waveguide system. For practical reasons, the number of rings is not increased above three. With a larger number of rings the aperture width of the waveguides should become very small, which will probably result in inefficient antennas. Apart from the operating frequency and the number of rings, Seebass et al. also studied the impact of the number of antennas per ring, but in the present study the number of antennas per ring is fixed to four (top, bottom, left and right), as this is the most practical arrangement for rectangular waveguides because of the non-oblique angles. Based on our experience in clinical hyperthermia using waveguide systems we expect that the dimensions and rigidness of the waveguides will make it very difficult to guarantee effective coupling of the electromagnetic waves to tissue over the complete aperture and to avoid air gaps between the water boluses for different arrangements. Treatment planning was applied to investigate the impact of the operating frequency of an eight-waveguide system (organised in two rings of four antennas; similar to the 70-MHz AMC-8 system) on the tumour temperatures that can be achieved. The potential additional gain of adding a third ring of waveguides was also investigated. Results were compared to the single-ring AMC-4 system.

Methods

Hyperthermia treatment planning was applied to investigate the impact of the operating frequency on target heating for a two-ring eight-waveguide locoregional system, with similar antenna arrangement as the operational two-ring 70-MHz AMC-8 system. The heating effectiveness at higher frequencies was compared to the operational single-ring 70-MHz AMC-4 system. The possible additional advantage of a third ring with four waveguides was examined as well.

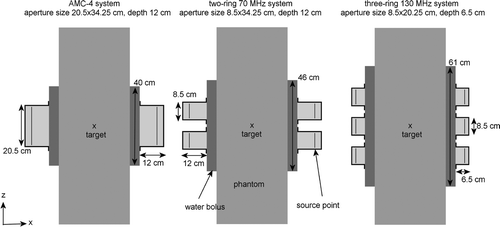
The aperture size of the operational 70-MHz AMC-4 and AMC-8 systems is 20.2 × 34.3 cm². The short side of the aperture is positioned parallel to the longitudinal axis of the patient, as illustrated in Figure 1 for a phantom set-up. To ensure that the two-ring system design resulting from this study is also suitable to treat short patients, all virtual 3D systems examined in this study had an aperture width of 8.5 cm instead of 20.2 cm. This is justified by results of our previous simulation study, which showed that the tumour temperatures that could be realised at 70 MHz with aperture sizes in the range of 20.5 × 34.25 cm² to 8.5 × 34.25 cm² were comparable [17]. The waveguides are filled with distilled water. Simulations were performed for frequencies of 70, 100, 120, 130, 140 and 150 MHz, where the current operating frequency of 70 MHz served as a reference. The length of the largest side of the aperture determines the cut-off frequency of the TE₁₀ mode and is therefore adapted to the desired frequency.

Figure 1. Model cross-sections of an elliptical phantom in the single-ring 70-MHz AMC-4 system and two and three-ring waveguide systems at 70 and 130 MHz, respectively.

For a waveguide aperture size a × b m², the cut-off frequency f_nm is calculated by Equation 1 [21]:where c is the speed of light in vacuum and ε_r is the dielectric constant of the medium inside the waveguides (ε_r of water is 80). With n = 1 and m = 0, it follows from Equation 1 that the cut-off frequency f₁₀ for the TE₁₀ mode is

To avoid the incidence of higher order modes, which are difficult to control, the aperture size of the waveguides was adapted such that only the TE₁₀ mode is excited at the selected frequency. The depth of the modelled waveguides was a quarter of the wavelength (λ) in water (see Figure 1). Table I shows the modelled aperture sizes and depths for each frequency and configuration. The waveguide's choke was modelled at a distance λ/16 of the back wall.

Table I.  Modelled waveguide aperture sizes and depths for different operating frequencies.

	70 MHz	100 MHz	120 MHz	130 MHz	140 MHz	150 MHz
Single ring 8.5 × 34.25 cm^2	*
Two rings 8.5 × 34.25 cm^2	*
8.5 × 30.25 cm^2	*	*
8.5 × 25.25 cm^2	*	*	*
8.5 × 20.25 cm^2		*	*	*	*	*
Three rings 8.5 × 20.25 cm^2		*	*	*	*	*
Waveguide depth (cm)	12	8.5	7	6.5	6	5.5

*Specific combination of frequency and waveguide configuration was modelled.

E-field simulations were performed using the finite-difference time-domain (FDTD) method to solve Maxwell's equations. A perfectly matched layer [22] was applied as absorbing boundary condition to truncate the computational domain. The resolution of the numerical simulations was x × y × z = 2.5 × 2.5 × 5 mm³, where z corresponds to the patient's longitudinal axis. For the single-ring AMC-4 system and the two-ring systems the water bolus covered a length of 40 and 46 cm in axial direction, respectively. For the three-ring systems the modelled bolus length was 61 cm (see Figure 1). The water bolus thickness was 5 cm, which corresponds to the clinical bolus thickness. The distance between the rings was set to 1.5 cm. The target is always positioned centrally, i.e. in between the two rings of a two-ring system; at the transversal mid-plane of the waveguides of the AMC-4 system or at the transversal mid-plane of the central ring of a three-ring system, as illustrated in Figure 1.

Phantom simulations

E-field distributions were simulated for an elliptical muscle-equivalent phantom with and without a 1-cm thick surrounding fat layer. Dimensions of the modelled phantoms were 36 × 24 × 100 cm³. The muscle-equivalent material of the phantom was modelled as a saline solution (3 g l⁻¹ NaCl, σ = 0.55 S m⁻¹ and ε_r = 75 @ 70 MHz) [23]. The dielectric properties of the fat layer at 70 MHz were modelled as σ = 0.06 S m⁻¹ and ε_r = 10. Dielectric properties of the saline solution do not change significantly in the range from 70–150 MHz [24] and were kept constant. For the fat layer the electrical conductivity was σ = 0.06 S m⁻¹ in this frequency range and the dielectric constant ε_r was 9 for frequencies of 100 MHz and higher [25].

The centre of the phantom was defined as target location. Optimisation of the phase/amplitude settings was performed for each frequency and configuration to compare the heating capability. The function:was optimised, where V₁ is the first volume percentile of the cylindrical phantom shell enclosing the fat layer (if present) and a 1-cm thick muscle layer, excluding both ends of the phantom. During optimisation the SAR was computed for the voxels in this shell over the axial length covered by the water boluses, and the average SAR was determined over the above mentioned maximum first percentile [17]. SAR optimisation was performed using a standard steepest descent method [26] and ten runs were performed with random feed vectors. In order to avoid clinically irrelevant settings (e.g. a single antenna delivering almost all power or an antenna contributing practically no power), constraints were set to the output power of each waveguide. An antenna of the AMC-4 system should deliver at least 10% and at most 40% of the total applied power; for a two-ring system this was at least 5% and at most 25%. For a three-ring system the minimum and maximum output power of each waveguide was constrained to 3% and 15% of the total power, respectively.

The SAR distributions were judged by their S_ratio, which is defined as the ratio between the maximum SAR in the phantom and the SAR in the target [13]:The lower the S_ratio, the less severe the SAR hot spots, which implies a better ability to heat the tumour with minimal side effects. The solution with the lowest S_ratio was selected to be the optimum.

Patient simulations

Simulations were performed for five cervical cancer patients to determine the clinical potential of two- and three-ring waveguide systems to heat a deep-seated target at different operating frequencies. These patients were treated with regional hyperthermia at the AMC. The same patient set as in the simulation study by Kok et al. [17] was used in the present study, to facilitate comparison with previous results. A CT scan of 60 cm (5 mm slice thickness) was made in treatment position, on a water bolus and mattresses identical to those applied during treatment. A radiation oncologist manually outlined the tumour and the rest of the CT data set was segmented automatically into muscle, fat, bone, air and lung tissue based on the CT Hounsfield units [27]. The segmented data set was downscaled to 2.5 × 2.5 × 5 mm³, using the ‘winner takes all’ method [28]. To avoid unwanted edge effects, the patient anatomy was extended to 1 m by repeatedly duplicating the last slice at the cranial and caudal sides.

Temperature-based optimisation was performed to simulate optimal tumour heating, while preventing overheating of normal tissue. The efficient optimisation method developed by Das et al. [29] was applied, which is based on the steady-state solution of Pennes’ bio heat equation [30]. Hard constraints of 45°C were applied to normal tissue temperatures. A threshold objective function was minimised to aim for a tumour temperature of 43°C:This function was optimised using C routines for Feasible Sequential Quadratic Programming (CFSQP) version 2.5 d [31]. Power constraints were set to each waveguide. An antenna of the AMC-4 system should deliver at least 10% and at most 40% of the total applied power; for a two-ring system this was at least 5% and at most 25%. For a three-ring system the minimum and maximum output power of each waveguide was constrained to 3% and 15% of the total power, respectively. At our department the temperature of the cooling water bolus is approximately 12°C during clinical hyperthermia [32]. Therefore, the temperature of the water bolus was kept constant at 12°C in the numerical simulations. Ten independent runs with a random initial phase/amplitude setting were performed to avoid a solution representing a local optimum and the solution with the lowest value for Equation 5 was selected as the optimal solution. Tissue properties at different frequencies were obtained from literature [25], [33]; Tables II and III list the dielectric and thermal properties applied in the simulations.

Table II.  Values of the dielectric properties for different tissue types at the frequencies applied in the simulations; conductivity (σ [S m⁻¹]), relative permittivity (ε_r [-]).

	70 MHz	100 MHz	120 MHz	130 MHz	140 MHz	150 MHz
Air σ (S m^−1)	0	0	0	0	0	0
εr (-)	1	1	1	1	1	1
Bone σ (S m^−1)	0.05	0.05	0.06	0.06	0.06	0.06
εr (-)	10	9	9	9	9	9
Fatty tissue σ (S m^−1)	0.06	0.06	0.06	0.06	0.06	0.06
εr (-)	10	9	9	9	9	9
Lung σ (S m^−1)	0.2	0.21	0.21	0.22	0.22	0.22
εr (-)	20	18	17	16	16	16
Muscle σ (S m^−1)	0.75	0.77	0.78	0.78	0.78	0.79
εr (-)	75	70	68	67	66	66
Phantom σ (S m^−1)	0.55	0.55	0.55	0.55	0.55	0.55
εr (-)	75	75	75	75	75	75
Tumour σ (S m^−1)	0.74	0.78	0.80	0.81	0.82	0.83
εr (-)	65	58	55	54	53	52

Table III.  Values of the thermal properties for different tissue types used in the simulations; density (ρ [kg m⁻³]), specific heat capacity (c [J kg⁻¹°C⁻¹]), thermal conductivity (k [W m⁻¹°C⁻¹]) and perfusion (W_b [kg m⁻³s⁻¹]).

	(ρ [kgm^−3])	(c [J kg^−1°C^−1])	(k [Wm^−1°C ^−1])	(Wb [kgm^−3s^−1])
Air	1.29	10000*	0.024	0.0
Bone	1595	1420	0.65	0.12
Fatty tissue	888	2387	0.22	1.1
Lung	750	3000	0.25	3.6
Muscle	1050	3639	0.56	3.6
Tumour	1050	3639	0.56	1.8

*The value of c used for air was ten times too high in order to allow larger time steps in thermal computations. This has a negligible effect on the steady-state temperature distribution.

For the resulting optimised temperature distribution, tumour temperatures were expressed as T₁₀, T₅₀ and T₉₀, i.e. the temperatures at least achieved in 10%, 50% and 90% of the tumour volume, respectively. The amount of power needed to realise the optimal tumour temperature was also determined.

Thermal iso-effect dose

For a hyperthermia treatment, the thermal iso-effect dose is usually expressed as the number of equivalent min at 43°C. The number of equivalent min at 43°C (Δt_eq) is calculated by Equation 6 [34]:

For the current temperature T in Equation 6 the simulated optimal T₉₀ was applied, which is a measure for the minimum temperature and usually most significant for clinical outcome. A standard treatment time Δt of 60 min was assumed. The thermal iso-effect dose was used as a measure to quantify the effectiveness of the different frequencies and different ring configurations.

Results

Phantom simulations

The effectiveness of the different frequencies and ring configurations was compared by determining the S_ratio of the optimised SAR distribution and comparing optimised SAR patterns. Resulting S_ratio values for both the homogeneous and the fat-muscle phantom are listed in Table IV.

Table IV.  Values of the S_ratio (i.e. the ratio between the maximum SAR in the phantom and the SAR in the central target) for both the homogeneous and the fat-muscle phantom after SAR optimisation. Constraints were set to the output power of each waveguide: an antenna of the single-ring AMC-4 system should deliver at least 10% and at most 40% of the total applied power; for a two-ring system this was at least 5% and at most 25%. For a three-ring system the minimum and maximum output power of each waveguide was constrained to 3% and 15% of the total power, respectively.

	70 MHz	100 MHz	120 MHz	130 MHz	140 MHz	150 MHz
Homogeneous muscle
Single ring 8.5 × 34.25 cm^2	1.62
Two rings 8.5 × 34.25 cm^2	1.4
8.5 × 30.25 cm^2	1.5	1.53
8.5 × 25.25 cm^2	1.78	1.64	1.49
8.5 × 20.25 cm^2		1.98	1.78	1.54	1.45	1.81
Three rings 8.5 × 20.25 cm^2		1.58	1.5	1.33	1.19	1.65
Fat-muscle
Single ring 8.5 × 34.25 cm^2	1.63
Two rings 8.5 × 34.25 cm^2	1.47
8.5 × 30.25 cm^2	1.62	1.72
8.5 × 25.25 cm^2	1.75	1.22	1.5
8.5 × 20.25 cm^2		1.26	1.8	1.55	1.37	1.59
Three rings 8.5 × 20.25 cm^2		1.1	1.03	1.02	1.04	1.36

The lowest S_ratio values for the three-ring systems are written in bold type.

The values in Table IV show that for the homogeneous phantom 70 MHz provides the lowest S_ratio in the case of a two-ring system. For a three-ring system the homogeneous phantom shows a decreasing S_ratio with increasing frequency up to 140 MHz, where the S_ratio is 1.19. At 140 MHz the S_ratio for a two-ring system only 3.5% higher than the S_ratio at 70 MHz. This makes 140 MHz a favourable frequency for both a two-ring and a three-ring system when heating a homogenous phantom. The relative improvement in S_ratio at 140 MHz is 10% and 27% compared to the single-ring 70-MHz AMC-4 system for two and three rings, respectively. For a fixed frequency, e.g. 70, 100 or 120 MHz, the S_ratio increases with decreasing aperture size, which can be explained by the fact that power is coupled into the phantom over a smaller surface, thereby increasing the risk of hot spots.

The fat-muscle phantom also shows the pattern of an increasing S_ratio with decreasing aperture size for a fixed frequency, with exception of 100 MHz. At 100 MHz a smaller aperture has a favourable effect on the S_ratio, which implies a favourable distance between the antennas and the hot spots to minimise the hot spot SAR by interference. Since this favourable result is obtained with a relatively simple fat-muscle phantom, it is not very likely that this ‘ideal’ configuration will also stand out for more realistic and very heterogeneous patient anatomies. Apart from this exceptional case 140 MHz yields the optimal S_ratio for a fat-muscle phantom heated with a two-ring system. However, the relative difference in S_ratio compared to a two-ring 70-MHz system is only 7%. For a three-ring system the S_ratio at 120, 130 and 140 MHz is very close to 1. At 140 MHz, the relative improvement in S_ratio is 16% and 36% compared to the single-ring 70-MHz AMC-4 system for two and three rings, respectively. Results from Table IV indicate a favourable heating pattern at 140 MHz, for both a homogenous and a fat-muscle phantom with both two-ring and three-ring waveguide systems. As indicated by the S_ratio, a three-ring system allows a more homogenous SAR distribution, which can be explained by the fact that the power emitted by the waveguides is distributed over a larger volume. This suggests a lower incidence of treatment-limiting hot spots in clinical applications.

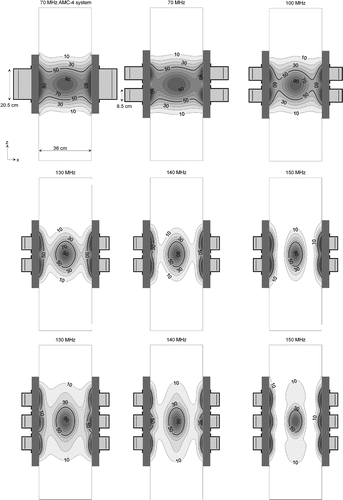
Figure 2 shows coronal cross-sections of the optimised SAR distributions for the homogeneous phantom for different operating frequencies and configurations. For frequencies and configurations for which multiple aperture sizes were simulated, results for the largest aperture size are shown. SAR distributions were normalised such that the central voxel (=target) corresponds to 100%. With increasing frequency the central focus becomes smaller and non-superficial normal tissue heating decreases. Thus, in addition to the improved S_ratio, the heating patterns at higher frequencies as shown in Figure 2 are favourable since the overall power absorption in normal tissue is significantly lower compared to 70 MHz. This is likely to provide the possibility of increasing the target temperature in the clinic without overheating normal tissue, but on the other hand a small SAR focus can be disadvantageous for larger target volumes. Simulations for real patient anatomies should provide more insight into the clinical heating capability.

Figure 2. Optimised SAR distributions in the homogeneous muscle-equivalent phantom for the 2D single-ring 70 MHz AMC-4 system and 3D double-ring and triple-ring systems at different operating frequencies. Slices were taken in the central xz-plane. For frequencies and configurations for which multiple aperture sizes were simulated, results for the largest aperture size are shown.

Patient simulations

Phantom simulations suggest a more favourable with heating at higher frequencies and multiple rings. To what extent this is also true in more clinically relevant situations will be shown by patient simulations. Temperature-based optimisation was performed for five cervical cancer patients. The resulting indexed temperatures T₁₀, T₅₀ and T₉₀ were compared for the different operating frequencies and configurations, as well as the total absorbed power needed to realise those temperatures.

For the 70, 100 and 120-MHz two-ring systems, the impact of the aperture size on the achieved tumour temperatures was determined. Results are shown in Tables V–VII for 70, 100 and 120 MHz, respectively. The reported indexed temperatures were fairly different for these five patients, indicating a varied patient group. For each patient the achieved temperatures were generally similar for a fixed frequency, but for some cases small deviations were observed. For example patient 5 showed a slightly lower T₉₀ at 70 MHz for an aperture size of 8.5 × 30.25 cm² and at 120 MHz for an aperture size of 8.5 × 20.25 cm². The average improvement in indexed temperatures with respect to the AMC-4 system (as shown in the last columns of Tables V–VII) did not change much when varying the aperture size. This demonstrates that the aperture size has a minor impact on the achieved tumour temperatures.

Table V.  Optimised indexed tumour temperatures for five cervical cancer patients and the total absorbed power at 70 MHz for aperture sizes 8.5 × 34.25 cm², 8.5 × 30.25 cm² and 8.5 × 25.25 cm². The last column lists the amount of power and the gain in temperature with respect to the single-ring 70-MHz AMC-4 system averaged over the five patients.

70 MHz	Patient 1	Patient 2	Patient 3	Patient 4	Patient 5	Average gain (°C) w.r.t. AMC-4/average power (W)
34.25 cm T90 (°C)	40.3	40.3	40.9	41.0	41.0	0.4
T50 (°C)	41.1	41.8	41.6	42.0	43.0	0.6
T10 (°C)	41.9	42.8	42.4	43.8	44.2	0.7
Power (W)	803	681	635	662	674	691
30.25 cm T90 (°C)	40.2	40.3	40.8	41.0	40.6	0.3
T50 (°C)	41.0	41.8	41.6	42.0	42.5	0.5
T10 (°C)	41.9	42.9	42.3	43.7	43.8	0.6
Power (W)	808	694	620	647	669	688
25.25 cm T90 (°C)	40.2	40.3	40.7	40.9	40.8	0.3
T50 (°C)	41.0	41.7	41.5	41.9	42.6	0.4
T10 (°C)	41.8	42.7	42.2	43.8	44.1	0.6
Power (W)	759	657	588	617	675	659

Table VI.  Optimised indexed tumour temperatures for five cervical cancer patients and the total absorbed power at 100 MHz for aperture sizes 8.5 × 30.25 cm², 8.5 × 25.25 cm² and 8.5 × 20.25 cm². The last column lists the amount of power and the gain in temperature with respect to the single-ring 70-MHz AMC-4 system averaged over the five patients.

100 MHz	Patient 1	Patient 2	Patient 3	Patient 4	Patient 5	Average gain (°C) with respect to AMC-4/average power (W)
30.25 cm T90 (°C)	40.6	40.7	41.7	41.5	41.1	0.8
T50 (°C)	41.6	42.4	42.4	42.7	43.1	1.1
T10 (°C)	42.6	43.6	43.1	44.5	44.6	1.3
Power (W)	746	702	609	616	642	663
25.25 cm T90 (°C)	40.8	40.6	41.7	41.3	41.2	0.8
T50 (°C)	41.9	42.4	42.5	42.5	43.4	1.2
T10 (°C)	42.9	43.7	43.3	44.0	45.0	1.4
Power (W)	770	665	594	610	715	671
20.25 cm T90 (°C)	40.8	40.6	41.7	41.2	41.2	0.8
T50 (°C)	41.9	42.4	42.4	42.4	43.4	1.2
T10 (°C)	42.9	43.6	43.2	44.1	45.1	1.4
Power (W)	793	683	581	615	692	673

Table VII.  Optimised indexed tumour temperatures for five cervical cancer patients and the total absorbed power at 120 MHz for aperture sizes 8.5 × 25.25 cm² and 8.5 × 20.25 cm². The last column lists the amount of power and the gain in temperature with respect to the single-ring 70-MHz AMC-4 system averaged over the five patients.

120 MHz	Patient 1	Patient 2	Patient 3	Patient 4	Patient 5	Average gain (°C) with respect to AMC-4/average power (W)
25.25 cm T90 (°C)	41.0	41.1	42.0	41.8	41.8	1.2
T50 (°C)	42.2	42.6	42.8	43.1	43.5	1.5
T10 (°C)	43.3	43.8	43.6	44.6	44.8	1.7
Power (W)	832	707	611	585	814	710
20.25 cm T90 (°C)	41.0	41.1	42.1	41.8	41.2	1.1
T50 (°C)	42.0	42.7	43.0	43.1	43.1	1.5
T10 (°C)	43.0	43.9	43.7	44.6	44.2	1.5
Power (W)	840	679	624	637	740	704

An overview of the results per patient for the complete frequency range of the two-ring waveguide systems (70–150 MHz) is shown in Table VIII. Optimised temperatures and total absorbed power are listed for these systems as well as for the single-ring AMC-4 system. If multiple aperture sizes were simulated, results for the largest aperture size are shown (70 MHz: 8.5 × 34.25 cm², 100 MHz: 8.5 × 30.25 cm², 120 MHz: 8.5 × 25.25 cm²). The average gain in indexed temperatures compared to the single-ring AMC-4 system over these five patients and the average amount of power are plotted in Figure 3.

Figure 3. Gain in optimised indexed temperatures T₁₀, T₅₀ and T₉₀ (left) with respect to the single-ring 70-MHz AMC-4 system and the corresponding total amount of absorbed power (right) for two-ring waveguide systems at different operating frequencies. Results are averaged over the five patients.

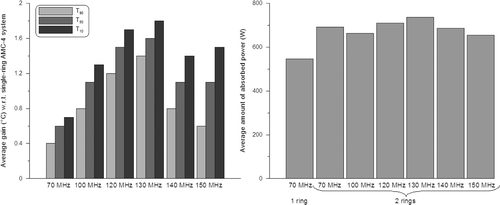
Table VIII.  Optimised indexed tumour temperatures for five cervical cancer patients and the total absorbed power using the single-ring AMC-4 system and two-ring waveguide systems at different frequencies. At frequencies for which multiple aperture sizes were simulated, results for the largest aperture size are shown (70 MHz: 8.5 × 34.25 cm², 100 MHz: 8.5 × 30.25 cm², 120 MHz: 8.5 × 25.25 cm²). The highest T₉₀ for each patient is written in bold type.

	Patient 1	Patient 2	Patient 3	Patient 4	Patient 5
AMC-4 T90 (°C)	39.8	40.1	40.7	40.6	40.3
70 MHz T50 (°C)	40.5	41.3	41.3	41.6	41.9
T10 (°C)	41.3	42.3	42.0	43.3	42.9
Power (W)	606	552	549	527	494
Two-ring systems
70 MHz T90 (°C)	40.3	40.3	40.9	41.0	41.0
T50 (°C)	41.1	41.8	41.6	42.0	43.0
T10 (°C)	41.9	42.8	42.4	43.8	44.2
Power (W)	803	681	635	662	674
100 MHz T90 (°C)	40.6	40.7	41.7	41.5	41.1
T50 (°C)	41.6	42.4	42.4	42.7	43.1
T10 (°C)	42.6	43.6	43.1	44.5	44.6
Power (W)	746	702	609	616	642
120 MHz T90 (°C)	41.0	41.1	42.0	41.8	41.8
T50 (°C)	42.2	42.6	42.8	43.1	43.5
T10 (°C)	43.3	43.8	43.6	44.6	44.8
Power (W)	832	707	611	585	814
130 MHz T90 (°C)	40.9	41.2	42.3	41.9	42.2
T50 (°C)	41.9	42.7	43.2	43.3	43.7
T10 (°C)	42.9	43.9	44.0	44.9	44.9
Power (W)	932	747	620	628	755
140 MHz T90 (°C)	39.4	40.6	42.1	41.8	41.7
T50 (°C)	40.0	42.0	43.1	43.3	43.9
T10 (°C)	40.9	43.2	44.1	45.1	45.5
Power (W)	750	688	650	637	705
150 MHz T90 (°C)	40.5	40.6	40.3	41.7	41.5
T50 (°C)	41.2	42.2	41.3	43.1	44.1
T10 (°C)	42.4	43.7	42.3	44.9	45.8
Power (W)	778	637	565	641	655

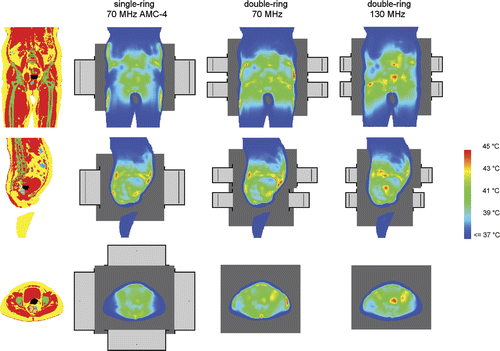
The results from Table VIII and Figure 3 show that an operating frequency of 130 MHz yields the highest tumour temperatures for a two-ring configuration. The tumour temperatures gradually increase with increasing frequency up to 130 MHz and at 140 MHz the temperatures decrease. The T₉₀ at 130 MHz was on average 1.4°C higher in comparison to the single-ring AMC-4 system, where the 70-MHz system resulted in a 0.4°C increase in T₉₀. The amount of power needed to realise optimal tumour temperatures was comparable for all two-ring systems. Averaged over the five patients, the amount of absorbed power was only ∼7% higher for 130 MHz compared to 70 MHz. Figure 4 shows an example of a temperature distribution optimised for the AMC-4 system and eight-waveguide systems at 70 and 130 MHz. These temperature distributions for patient 3 clearly show the improved target heating at 130 MHz.

Figure 4. Coronal (top), sagittal (centre) and transversal (bottom) slices of the anatomy of patient 3 (left column). Red corresponds to muscle tissue, fat tissue is yellow, bone is green and inner air is blue. The tumour is represented by the black spot in the centre. The other three columns show the temperature distributions optimised for the 70-MHz AMC-4 system and double-ring systems at 70 and 130 MHz. Left and right of the patient correspond with right and left in these pictures, respectively. The orthogonal slices run through the centre of gravity of the tumour.

Table IX shows the optimised tumour temperatures and the corresponding amount of total absorbed power for three-ring waveguide systems at different frequencies (100–150 MHz). For reference, the results for the 130-MHz two-ring system (optimum of the two-ring systems) are listed again as well as the results for the single-ring AMC-4 system. The achieved T₉₀ for each patient is plotted in Figure 5. The average gain in indexed temperatures compared to the single-ring AMC-4 system over these five patients and the average amount of absorbed power are plotted in Figure 6.

Figure 5. Optimised T₉₀ for each patient simulated with three-ring systems at different operating frequencies. For comparison the optimised T₉₀ with the 70-MHz AMC-4 system and with a two-ring system at 130 MHz (optimum of the two-ring systems) are plotted as well.

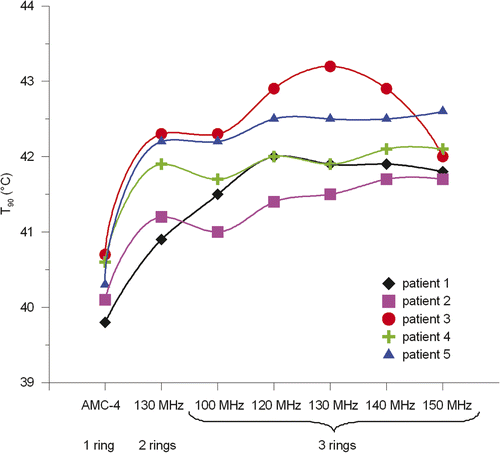
Figure 6. Gain in optimised indexed temperatures T₁₀, T₅₀ and T₉₀ (left) with respect to the single-ring 70-MHz AMC-4 system and the corresponding total amount of absorbed power (right) for three-ring waveguide systems at different operating frequencies. Results are averaged over the five patients. For comparison, the results for the optimal double-ring system at 130 MHz are plotted as well.

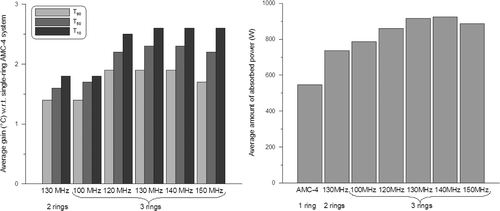
Table IX.  Optimised indexed tumour temperatures for five cervical cancer patients and the total absorbed power using three-ring waveguide systems at different frequencies. For reference the optimised results for the single-ring AMC-4 system are repeated here as well as for the optimal frequency for a two-ring system (130 MHz).

	Patient 1	Patient 2	Patient 3	Patient 4	Patient 5
AMC-4 T90 (°C)	39.8	40.1	40.7	40.6	40.3
70 MHz T50 (°C)	40.5	41.3	41.3	41.6	41.9
T10 (°C)	41.3	42.3	42.0	43.3	42.9
Power (W)	606	552	549	527	494
Two-ring system
130 MHz T90 (°C)	40.9	41.2	42.3	41.9	42.2
T50 (°C)	41.9	42.7	43.2	43.3	43.7
T10 (°C)	42.9	43.9	44.0	44.9	44.9
Power (W)	932	747	620	628	755
Three-ring systems
100 MHz T90 (°C)	41.5	41.0	42.3	41.7	42.2
T50 (°C)	42.6	42.6	43.3	42.9	43.9
T10 (°C)	43.7	43.8	44.2	43.8	45.3
Power (W)	871	762	742	719	842
120 MHz T90 (°C)	42.0	41.4	42.9	42.0	42.5
T50 (°C)	43.2	43.2	43.9	43.3	44.1
T10 (°C)	44.5	44.5	44.9	44.8	45.5
Power (W)	1059	885	735	779	838
130 MHz T90 (°C)	41.9	41.5	43.2	41.9	42.5
T50 (°C)	43.1	43.4	44.3	43.4	44.1
T10 (°C)	44.3	44.9	45.3	45.0	45.5
Power (W)	1147	914	784	749	984
140 MHz T90 (°C)	41.9	41.7	42.9	42.1	42.5
T50 (°C)	42.8	43.5	43.9	43.6	44.3
T10 (°C)	44.1	45.0	44.9	45.3	45.7
Power (W)	1178	905	729	787	1021
150 MHz T90 (°C)	41.8	41.7	42.0	42.1	42.6
T50 (°C)	43.1	43.7	43.0	43.7	44.3
T10 (°C)	44.6	45.2	44.0	45.4	45.8
Power (W)	1109	866	857	724	886

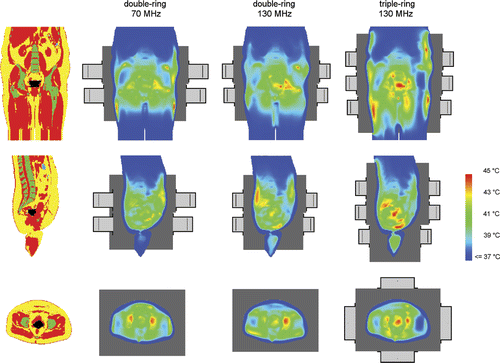
Table IX and Figures 5 and 6 suggest that the optimal frequency for a three-ring waveguide system is also around 130 MHz, but the optimum is not as clearly pronounced as for a two-ring system. A three-ring system realises a further increase in tumour temperatures (on average 0.5°C in T₉₀), but not for all patients. For example, for patients 1 and 3 the T₉₀ is about 1°C higher with three rings compared to two rings at 130 MHz, while for the other three patients T₉₀ was comparable or only 0.2–0.3°C higher with an additional ring at 130 MHz. For patient 4 all indexed tumour temperatures were comparable, while for patients 2 and 5 the additional ring showed a favourable effect (increase ≥ ∼0.5°C) on T₅₀ and T₁₀. Tables VIII and IX show that the largest improvement is achieved by increasing the frequency. The average total amount of absorbed power needed to realise optimal tumour temperatures increases with ∼25% for a three-ring system at 130 MHz, compared to a two-ring 130-MHz system. This can be explained by the fact that the distance from the waveguides to the target is larger for the outer two rings in comparison to a two-ring system. Figure 7 shows an example of an optimised temperature distribution for a two-ring system operating at 70 MHz and 130 MHz and a 130-MHz three-ring system. For this patient (patient 1) a third ring of waveguides clearly improves tumour coverage.

Figure 7. Coronal (top), sagittal (centre) and transversal (bottom) slices of the anatomy of patient 1 (left column). Red corresponds to muscle tissue, fat tissue is yellow, bone is green and inner air is blue. The tumour is represented by the black spot in the centre. The other three columns show the temperature distributions optimised for double-ring systems at 70 and 130 MHz and a three-ring system at 130 MHz. Left and right of the patient correspond with right and left in these pictures, respectively. The orthogonal slices run through the centre of gravity of the tumour.

Thermal iso-effect dose

The thermal iso-effect dose, i.e. the number of equivalent min at 43°C, was determined for the optimal T₉₀ for each patient at different frequencies and system configurations, which provides a better quantification of the achieved improvement. A standard treatment time of 60 min was assumed. Figure 8 shows the number of equivalent min at 43°C per waveguide system for each patient. The dotted grey line represents the number of equivalent min at 43°C when T in Equation 6 is the T₉₀ averaged over the five patients.

Figure 8. The number of equivalent min at 43°C for the T₉₀ of each patient according to Equation 6 plotted against the operating frequency. The left picture shows the improvement with a two-ring system at higher frequencies and the right picture with a three-ring system. The grey dotted line represents the result for the T₉₀ averaged over all five patients. A log-scale was used on the vertical axis. This graph emphasises the significant improvement in thermal dose delivery that can be achieved by increasing the operating frequency from 70 to 130 MHz.

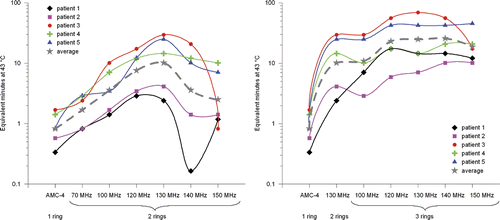
Figure 8 shows a significant gain in number of equivalent min at 43°C when increasing the operating frequency from 70 MHz to 130 MHz. On average (dotted line), a factor ∼2 improvement is achieved for a two-ring 70-MHz system compared to the single-ring AMC-4 system. For a two-ring and three-ring system operating at 130 MHz, this improvement is a factor ∼12 and ∼30, respectively.

Discussion

Previous research has shown that the 3D steering of a double-ring 70-MHz waveguide system leads to improved tumour temperatures in comparison to a single-ring 2D 70-MHz waveguide system [13], [35]. Numerical simulations also showed that it is possible to achieve a comparable improvement with smaller waveguide apertures of 8.5 × 34.25 cm² instead of 20.5 × 34.25 cm² [17]. The present simulation study investigated whether an additional gain in tumour temperature would be possible with the same waveguide configuration operating at a higher frequency. The aperture width of the waveguide of the two-ring systems modelled in this study was 8.5 cm, which was chosen such that the system is generally applicable as a two-ring system, also for short patients. For optimal treatment quality it could be useful to have a system that can be applied either as a two-ring or a three-ring system, dependent on the patient's length and tumour site. In view of this, the possible additional gain of adding a third ring of four waveguides, resulting in a 12-waveguide system, was investigated.

Seebass et al. conducted a similar study for a system with dipole antennas, in which apart from the number of rings and the operating frequency the number of antennas per ring were also varied. This resulted in a proposed system with three rings of dipoles operating at a frequency around 150 MHz and either eight dipoles or six paired dipoles per ring [14]. In the study described in the current paper, the highest tumour temperatures with a two-ring system were observed at 130 MHz. At this frequency the gain in T₉₀ was on average ∼1.5°C compared to the single-ring 70-MHz AMC-4 system, in comparison to ∼0.5°C for a two-ring 70-MHz system. For a three-ring system the optimal frequency was also 130 MHz, which yielded an average improvement in T₉₀ of ∼2°C compared to the AMC-4 system, but the results were very patient-dependent. For some patients a strong improvement was seen in comparison to a two-ring 130-MHz system, while for other patients the additional gain of the third ring was negligible. In the study by Seebass et al. the improvement by adding a third ring was also larger for some patients compared to others, but the gain with respect to two rings was relevant for all patients. The only exception was a patient with a peripherally located soft tissue sarcoma, where no significant hot spots occurred far away from the tumour due to its location in the upper thigh.

Dielectric and thermal properties applied in the simulations were obtained from literature and these values show a large spread [25], [33]. The uncertainties in tissue properties are too large for clinically reliable quantitative treatment planning for individual patients [36]. However, clinical verification studies showed a good correlation between simulation and clinical data [32], [37]. This makes treatment planning a valuable tool for qualitative predictions of SAR and temperature distributions, as applied in the present study. To compare different applicator designs, it is not necessary to predict the precise SAR and temperature distributions in the patient. Therefore, the impact of using a double-ring or triple-ring system or a different operating frequency can be studied adequately using average tissue properties from literature.

Understanding of the basic physics behind these locoregional waveguide systems can be improved using an analytical model. A cylindrical wave coupled into a homogeneous cylindrical phantom and the wave's behaviour with respect to the phantom dimensions, dielectric properties and operating frequency can be described by Bessel functions. A full mathematical analysis is beyond the scope of this paper, but for future research it would be interesting to compare results of a (simplified) analytical model with numerical simulations.

The improvement in tumour temperatures found in this study is comparable to the improvement observed in other simulation studies described in the literature when comparing 2D and 3D steering. For example, Wust et al. showed a 1–2°C improvement of the indexed tumour temperatures when upgrading the single-ring Sigma-60 to a triple ring system, both operating at 90 MHz [38]. Kroeze et al. found a similar improvement when comparing their proposed 3D regional hyperthermia open water bolus cavity slot (RHOCS) system at 150 MHz [15] consisting of 18 antennas organised in three rings of 6 antennas, with the 70-MHz coaxial TEM. However, the 8-waveguide system at 130 MHz proposed in this study has fewer antennas and thus fewer degrees of freedom compared to any of these systems. Evidently the number of possible system settings, and thus the difficulty to find the optimal setting increases significantly with the number of degrees of freedom. Taking into account the fact that hyperthermia treatment planning is presently not accurate enough for application in the clinic to individual patients, a 3D waveguide system with fewer degrees of freedom compared to the other 3D hyperthermia systems described in the literature is therefore expected to be more robust and easier to handle in clinical practice. Moreover, the possibility to use either two or three rings of waveguides provides additional flexibility.

The complexity of hyperthermia systems increases with the number of antennas and the number of rings. This implies that accurate treatment planning becomes increasingly important to fully exploit the benefits of these heating systems in the clinic. The impact of uncertainties in phase/amplitude settings are dependent on the number of antennas and frequency [14]. Small inaccuracies in generator output and variation in assumed tissue properties results in a deviation in prescribed optimal antenna settings. Seebass et al. found the sensitivity with respect to amplitudes and phases decrease with the frequency and increase with the number of antennas [14], dominated by amplitude errors. However, the applicator design studied by Seebass et al. [14], i.e. an elliptical applicator with eight or twelve dipole antennas (either paired or not), is very different from the rectangular waveguide system proposed in the present study and thus results described by Seebass et al. cannot be directly extrapolated to these waveguide systems. Therefore, additional sensitivity studies for waveguide systems are the subject of current research and results will be communicated in a future paper.

Conclusion

Simulations showed that a two-ring, 3D-steered, waveguide system yields significantly higher tumour temperatures at 130 MHz compared to both a two-ring and single-ring waveguide system at 70 MHz. For two-ring systems operating at 70 and 130 MHz the average gain in T₉₀ was about 0.5°C and 1.5°C, respectively, compared to the single-ring AMC-4 system with 2D steering. This implies an improvement in the thermal iso-effect dose (i.e. the number of equivalent min at 43°C) with a factor ∼2 and ∼12, respectively.

Tumour temperatures were further improved with a triple-ring waveguide system operating at 130 MHz. Simulations showed an average gain in T₉₀ of about 2°C compared to the single-ring AMC-4 system. This corresponds on average to a factor ∼30 increase in iso-effect dose, but the additional improvement compared to the 130 MHz double-ring system is very patient-dependent.

Declaration of interest: This study was supported by the Dutch Cancer Society (grant 2006-3484). The authors alone are responsible for the content and writing of the paper.