Mathematical models of laser-induced tissue thermal damage

Abstract

Laser sources are under increasing study for in vivo tumour ablation. Photo-thermal ablation in tissues varies tremendously in governing physical phenomena, depending on wavelength, owing to wide variation in the optical properties of tissues, specifically the dominant chromophore and degree and type of scattering. Once converted into local tissue heating, however, the governing thermodynamic principles remain the same. Observed irreversible thermal alterations range from substantial structural disruption due to steam evolution in high temperature short-term activations to low temperature rise, longer-term initiation of the complex protein cascades that result in apoptosis and/or necroptosis. The usual mathematical model in hyperthermia studies, the thermal isoeffect dose, arising from the relative reaction rate formulation, is not an effective description of the higher temperature effects because multiple processes occur in parallel. The Arrhenius formulation based on the theory of absolute reaction rates is much more useful and descriptive in laser heating since the multiple thermodynamically independent processes may be studied separately.

• laser
• modelling
• thermal ablation
• thermal dose
• kinetic models

Introduction

Laser heating of tissues for tumour ablation has developed into a viable clinical treatment option with the advent of image-guided therapies. The US Food and Drug Administration indexes approximately 11 000 articles related to clinical ablation devices [1]. In this context ‘ablation’ – from the Latin ‘ablatus’, past participle of ‘auffere’ to carry away [2] – is different from the usual engineering definition, ‘to create a mass defect’. Clinically, ablation means ‘to remove from the inventory of live tissue’, which may or may not include creating a mass defect. There are many thermodynamic processes at work in parallel during laser heating, each with different rates of development and temperature ranges over which they are likely to be observed. Consequently, describing them all with a single characterising parameter, such as the thermal isoeffect dose in terms of the cumulative equivalent minutes at 43°C, as is typical in hyperthermia studies, is not an effective approach at higher temperatures. It is much more informative and illuminating to apply an Arrhenius formulation based on absolute reaction rates to follow the development of the multiple thermodynamically independent damage processes in parallel individually. A review of those processes and their description in these terms is the subject of this paper, organised from higher to lower temperature processes.

The fundamental relationship in tissue heating in the absence of phase change is the bio-heat equation:where ρ = density (kg m⁻³), h = specific enthalpy (J kg⁻¹) – Gibb's defined quantity meaning the total heat or heat content [3] – c = specific heat (J kg⁻¹ K⁻¹), T = temperature (K), Q_gen = the laser heating term (W m⁻³), k = thermal conductivity (W m⁻¹ K⁻¹), w = tissue perfusion (kg_b kg⁻¹ s⁻¹) the ‘b’ subscript refers to blood properties (unsubscripted properties are those of tissue), and Q_met = metabolic heat (W m⁻³). The left hand side of the equation represents the transient local tissue-specific enthalpy, which is expressed in terms of the internal thermal energy, u = cT (J kg⁻¹), in the bioheat equation. The source term in the bioheat equation, Q_gen = μ_aΦ, where μ_a is the absorption coefficient (m⁻¹) and Φ is the local laser beam fluence rate (W m⁻²) – μ_a refers specifically to optical absorption losses, and does not include extinction or attenuation due to scattering. For typical laser heating applications the applied volumetric power density, Q_gen, is usually so high that both metabolic and perfusion heat are negligible. In fact, it will often be necessary to add terms to account for water vaporisation – water is the most thermodynamically active tissue constituent.

As has been described elsewhere in this issue, the particular laser wavelength strongly influences the spatial distribution of the volumetric power deposition term in Equation 1, Q_gen. Long wavelength CO₂ lasers, at λ = 10.6 µm, are primarily absorbed by tissue water, as are Ho:YAG, at 2.10 µm, and Tm:YAG, at 2.01 and 1.94 µm, and wavelengths in between. Scattering is negligible at those wavelengths; consequently, calculation of the thermal fields is relatively simple and a Beer's law formulation is sufficient. Of course, with water as the primary chromophore, inclusion of vaporisation effects is of critical importance, and is treated in this paper.

In contrast, at laser wavelengths less than about 1.1 µm other tissue constituents are the primary chromophores and absorption by water is negligible in comparison. Nd:YAG at 1064 nm is very highly scattered, with a significant forward-scattering component, and consequently penetrates much deeper into tissues. Between about 700 and 1100 nm there are very few one-photon absorber chromophores [4] and scattering is a dominant effect [5]. Near-infrared diode lasers around 800 nm have found many applications in multi-photon and fluorescence imaging because of their more effective penetration [4]. More recently, appropriately sized and shaped gold nanoparticles or nanoshells have been used to target specific sites with diode laser illumination at this wavelength. The physics of this application rely on an extremely interesting quantum physical process known as plasmon resonance [6–11].

KTP (frequency-doubled Nd:YAG) at 532 nm, and Argon lasers at 514 nm are similar highly scattered wavelengths absorbed by tissue chromophores other than water; melanin and haemoglobin are two prominent examples. Often a dye – such as indocyanine green (ICG) [12] or fluorescein [13] – is used to enhance the absorption, or to target specific sites. Predicting the spatial distribution of the ‘fluence rate’ (W m⁻²) is complicated, and usually requires stochastic computation methods, such as a Monte Carlo approach, to obtain Q_gen [14]. Further, internal surface reflections and back-scattering at a tissue–air interface can result in the accumulation of sub-surface fluence rates three times (or more) the incident laser beam fluence rate just below the surface [14]. The subsurface effects are amplified when highly compartmentalised tissues, such as large arteries, are illuminated [15].

Ultraviolet excimer (excited dimer) lasers at wavelengths between 193 and 300 nm – ArF, XeCl and the like – have extremely high absorption coefficients and their penetration depths are on the order of 1 µm owing to absorption by amino acids. Similar penetration depths obtain at 1.94 µm owing to water absorption, while CO₂ lasers penetrate up to about 20 µm in water [16]. Between 600 nm and 1.1 µm the penetration depths are as much as several mm (up to almost 1 cm at 1064 nm) [14]. The relative optical properties strongly influence the irreversible thermal alterations realised.

High temperature effects: Water vaporisation

At the extremely short wavelengths characteristic of excimer lasers the tissue water is vaporised so rapidly that there is no time for heat transfer to create radiating thermal damage. These lasers are often described as ‘cold lasers’ since their photon energies break chemical bonds, but it should be borne in mind that the primary physics of the laser result in a debris plume driven by high pressure explosive vaporisation of water. Other laser types also vaporise significant amounts of water at high fluence rates, especially lasers for which the primary chromophore is water.

When water vaporisation is included it makes a significant contribution to the energy balance of Equation 1 due to the phase change enthalpy, Δh_fg (J kg⁻¹):where P_sat = the saturation pressure (Pa = N m⁻²), and v_fg = the specific volume (m³kg⁻¹) change during vaporisation (i.e. the ‘f’ subscript refers to the saturated liquid and ‘g’ to the saturated gas phase) and Δs_fg = the phase change entropy (J kg⁻¹ K⁻¹). Constant pressure equilibrium boiling has been assumed in this formulation, ΔP = 0. The constant pressure assumption is valid as long as evolved vapour can migrate readily through tissue structures – if this is not so, detailed structural characteristics, mechanical properties of tissues and mass diffusion coefficients are required. Equilibrium boiling means that the vaporisation process is not rate-limited, that water vapour can evolve as rapidly as necessary to maintain thermodynamic equilibrium, and ΔT ∼ 0 at the saturation temperature, T_sat. It is equivalent to assuming that the tissues contain a large number of potential nucleating sites for vapour formation, heterogeneous nucleation. Consequently, the phase change enthalpy, Δh_fg, does not include some form of energy of dissociation of liquid phase molecules, Δg (J kg⁻¹), which would determine the rate of vapour formation. This assumption is not restrictive for the usual laser ablation case, in which the heating rates are moderate. However, in very short pulse high fluence laser spots (order of ns to μs), some considerable superheating of liquid phase water is likely to exist, the boiling process may well be rate-limited, and substantial spikes in the local pressures result, which form the driving force for a debris plume. In those instances an additional rate equation for nucleation of vapour bubbles may be necessary, such as fundamentally described by Skripov [17], or more clearly by Gerum et al. [18].

The phase change effects for the slower boiling processes of this model appear in the tissue enthalpy on the left hand side of Equation 1:where the pressure–volume terms in the brackets refer to the remaining tissue water, and ∂m/∂t is the specific mass of tissue water vaporised (kg m⁻³s⁻¹). The pressure and density terms on the left hand side are written in terms of temperature-dependent correlations derived from steam table data [3], as described by Pearce and Thomsen [19], which are also described in a recent review article [20]. As a practical matter, for saturated liquid water Δρ/ΔT is small – ρ varies from 997.4 at 23°C to 958 at 100°C.

A separate energy balance is required for the evolved gas phase, involving compressibility effects and tissue yield strengths. Consequently, the mass diffusion rate of the evolved steam through the tissue strongly influences the net result, especially in highly stratified tissues.

As the tissue temperature reaches boiling point steam evolves at a very rapid rate – so rapid that a workable model for vaporisation is to consider it to be equilibrium boiling at the saturation temperature and to consume all of the laser heat in excess of that required to supply thermal conduction heat transfer. The build-up of pressures in tissue compartments can result in explosive rupture [15]. Vaporisation effects are often observed as ‘vacuoles’ in a tissue section; steam vacuoles are sometimes misclassified as adipose tissues since they have the same appearance in histologic section. Of course, a pressure build-up will increase the saturation pressure and consequently the equilibrium boiling temperature, complicating the calculation immeasurably.

Arrhenius formulations for thermal damage processes

The Arrhenius model is based on the kinetic model of relative reaction rates that the Swedish scientist Svante Arrhenius first formulated and described in 1889 [21], which was extended to the theory of absolute reaction rates in later studies. That original work – the founding pillar of physical chemistry –was published in German, and is well described by Johnson et al. in their first chapter [22]. Briefly, Arrhenius measured the rate of hydrolysis of sucrose in the presence of various acids in his original experiments. The observations indicated that the temperature dependence of the reaction rate was too great to be described by either the temperature effect on the kinetic energy of the molecules or on the dissociation of the acids. The measured reaction velocities, k (s⁻¹), at temperatures T₁ and T₂ (K) were related by:where q in Arrhenius's original work was an experimentally determined constant, determined later to be (effectively) twice the reaction activation energy (J mole⁻¹) divided by the gas constant, R (J mole⁻¹ K⁻¹). Equation 4 constitutes the theory of relative reaction rates, and has been applied in a slightly modified form in numerous hyperthermia studies to derive the temperature-history comparative parameter, CEM₄₃, an exposure time at the reference temperature (43°C) equivalent to that at the treatment temperature, T_i:where t_i (minutes) is the time at temperature T_i (°C). Since CEM (minutes) describes relative exposure times rather than reaction rates, R_CEM is defined as the ratio of equivalent exposure time for a 1°C increase above the reference temperature, T. It is, consequently, the reciprocal of the term in brackets in Equation 4, as shown in Equation 5, and is usually taken to be approximately 0.5 from the original work of Sapareto et al., based on their experiments with Chinese hamster ovary cells [23].

Arrhenius's original 1889 experimental work was later amplified to absolute reaction rates so that the ‘yield’ of a process could be calculated. In a uni-molecular formulation the reaction velocity, k (s⁻¹), is related to the remaining un-transformed molecular concentration, C, by a Bernoulli differential equation:for which the solution at time τ is:

In a reaction the velocity, k, is determined by the Gibbs free energy of activation, ΔG*. The activation enthalpy includes both the Gibbs free energy of activation and the activation entropy, ΔH* = ΔG* + TΔS*, so:where N = Avogadro's number (6.023 × 10²³ molecules mole⁻¹) and h_P= Planck's constant (6.63 × 10⁻³⁴ J s). In this formulation ΔH* = E_a− RT ∼ E_a, the activation energy barrier for a first order reaction (i.e. 1 ≪ ΔS*/R). In terms of a useful damage prediction, then, the remaining undamaged tissue constituent C(τ) is found from:and this formulation shows the relation to the classical damage parameter, Ω, as originally used by Henriques and Moritz, and many others since their pioneering thermal damage experiments [24–27]. From Equation 9(a) the probability of observing a particular thermal damage marker (or relative damage level) is then:

The multiple thermal damage processes each have an associated experimentally determined A and E_a pair, and separate process damage predictions can be accumulated as they develop in parallel, whether or not the processes are thermodynamically independent in a rigorous sense. A quantitatively measurable process is necessary; but, when available, enables direct comparison between model calculations and experimental analyses, such as histologic section or vital stain assay.

It is also sometimes instructive to look at the ‘critical temperature’ for a process, the temperature at which dΩ/dt = 1:

Functionally, the activation energy serves to indicate the relative ‘speed’ of the process – values lie between about 1 and 9 × 10⁵ (J mole⁻¹) – and ln{A} determines the temperature at which the process initiates.

Interestingly, according to Eyring et al. [28] the activation entropy varies over only a very narrow range of values. In April of 2003 Wright [29] used Eyring's observation, coupled with Miles and Ghelashvili's ‘polymer in a box’ construct [30] to explain an observed linear relationship between E_a and ln{A}, and obtained from a number of published data:where the units are those used to this point. Very slightly later in 2003 (and in a follow-up article in 2009) He and Bischof [31], [32] were able to fit a much wider range of experimental reports and processes with virtually the same result:

Either result may be used to evaluate the believability of experimentally determined coefficients, or to provide a necessary starting point for publications that only include the activation energy, E_a, as was done for several of the entries in Table I.

Table I.  Collected kinetic coefficients for representative thermal damage processes.

	Process parameters
Process	A (s^−1)	Ea (J mole^−1)	RCEM	Tcrit (°C)	Notes
Collagen changes
Maitland [35]	1.77 × 10^56	3.676 × 10^5		68.2	Rat tail birefringence
Pearce [34]	1.61 × 10^45	3.06 × 10^5		80.4	Rat skin birefringence
Aksan [77]	1.136 × 10^86	5.623 × 10^5		68.1	Rabbit patellar tendon
Miles [78]	6.658 × 10^79	5.21 × 10^5		67.8	Rat tail tendon, DSC
Chen [55–57]	1.46 × 10^66	4.428 × 10^5		76.4	Shrinkage, bovine chordae tendineae
Muscle
Jacques [79]	2.94 × 10^39	2.596 × 10^5	0.732	70.4	Myocardium whitening
Pearce (unpublished)	*4.341 × 10^51	3.365 × 10^5	0.678	67.2	Birefringence loss
Brown [65]	1.98 × 10^106	6.67 × 10^5	0.449	54.6	Microvessels in muscle
Erythrocytes
Lepock [59]	7.6 × 10^66	4.55 × 10^5		82.2	Haemoglobin denaturation
	*1.70 × 10^46	3.04 × 10^5	0.694	70.3	Haemolysis
Przybylska [62]	*1.08 × 10^44	2.908 × 10^5	0.707	71.8	Haemolysis, normal RBCs
	*3.7 × 10^43	2.88 × 10^5	0.708	72.1	Haemolysis, Down's Syndrome
Apoptosis/necrosis
Bhowmick [73]	7.78 × 10^22	1.61 × 10^5	0.824	94.2	H. prostate
McMillan [74]	2.29 × 10^29	1.895 × 10^5	0.797	64.0	Freshly excised tonsil
Cell death
Sapareto [80]	2.84 × 10^99	6.18 × 10^5	0.5	51.4	CHO cells, T > 43°C
Bhowmick [81]	1.66 × 10^91	5.68 × 10^5	0.508	52.1	AT-1 cells < 50°C
	173.5	1.97 × 10^4		186	AT-1 cells > 50°C
Borrelli [82]	2.984 × 10^80	5.064 × 10^5	0.547	55.5	BhK cells
He [83]	4.362 × 10^43	2.875 × 10^5	0.710	71.0	SN12 cells, suspended
	3.153 × 10^47	3.149 × 10^5	0.685	73.1	SN12 cells, attached

*Value for A is estimated from Equation 11(a).

Examples of quantitative thermal damage processes

A reasonable number of thermal damage processes have been studied to date to determine the required kinetic coefficients. The coefficients for the processes described in this paper are collected in Table I.

Collagen denaturation

Collagen is a ubiquitous structural protein that is birefringent in its native state – birefringence is the ability to rotate the polarisation of light – and collagen loses its regular rope-like structure, the origin of its birefringence, as bonds between the collagen macromolecules break due to thermal denaturation [33]. Denatured, or hyalinised (glassified), collagen is readily identified under transmission polarising microscopy (TPM) as a dark field, and makes a convenient quantitative marker of the boundary of this type of thermal damage. Rate coefficients for this thermal damage process have been measured and reported [34–36].

Jellification of collagen at higher temperatures is fundamental to tissue fusion processes, and has been applied in multiple clinical applications [12], [37–45]. Collagen also shrinks in length during denaturation at lower temperatures, approximately iso-volumically – a process used in many viable clinical applications [46–54]/ Chen et al. have presented a practical kinetic model for the collagen shrinkage process in bovine chordae tendineae that includes the effect of applied mechanical stress [55–57]. The curve fit functions utilise a non-dimensional time axis, t/τ₂, where the fit parameters are expressed in the form of the logarithm of the time ratio:The shrinkage is obtained by interpolation between two slow region curves (through a fast region):where a₀ = 1.80 ± 2.25; a₁ = 0.983 ± 0.937; b₀ = 42.4 ± 2.94; and b₁ = 3.17 ± 0.47 (all parameters in %). The best fit interpolation function, f(ν), is given by:where a = 2.48 ± 0.438, and ν_m = ln{τ₁/τ₂} = −0.77 ± 0.26. Finally, at any temperature τ₂ is given by:where α = −152.35; β = 0.0109 (kPa⁻¹); P = applied stress (kPa); and M = 53 256 (K).

The functional form of τ₂ contains the kinetic nature of the process, but is in the form of an exposure time rather than a rate of formation, as was used in Equation 9(a), and so the coefficient, M = E_a/R, is positive, and α = −ln{A}. To use the model, the shrinkage is referred to an equivalent τ₂. That is, at each point in space and time an equivalent value for the increment in t/τ₂ is calculated and accumulated until the total shrinkage is calculated at the end of heating. The total collagen shrinkage is limited to a maximum of about 60% – additional heating results in jellification of the collagen, which is the actual goal in tissue fusion applications [40–43], [58]. So, the collagen shrinkage model may be used for both types of application.

Birefringence loss in muscle

Skeletal, smooth and cardiac muscle also have strong birefringent properties that disappear when thermally denatured. The birefringence in muscle arises from the hexagonal regularity of the actin-myosin array [33], as sketched in Figure 1. Several estimates for Arrhenius coefficients for this process are given in Table I.

Figure 1. Figurative sketch of actin-myosin geometry that forms the regular structure responsible for the birefringent properties of the sarcomere. (A) Functional sarcomere unit cell (between z-bands). (B) Cross-section in the a-band.

Haemolysis of red blood cells

Haemolytic processes in red blood cells release haemoglobin into the blood stream for relatively low temperature increases in long-term exposures, such as sustained, very high fevers. Thermally induced haemolysis has been studied by a few investigators [59–63]. Przybylska et al. looked at haemolysis in normal and Down's syndrome patients [62] – there is virtually no significant difference between the two populations. In that work, only the activation energy was calculated; the value for A in Table I was estimated from Wright's line, Equation 11a, although the He–Bischof line, Equation 11(b), could just as well have been used. Haemolysis and denaturation of haemoglobin were studied by Lepock et al. [59].

Skin burns

The original Arrhenius thermal damage process was the production of skin burns by conduction heat transfer from an isothermal surface application. The classical work by Henriques and Moritz previously mentioned has been used by many investigators since its appearance. Relatively recently, Diller and Klutke [64] showed that the often-quoted coefficients in the original study do not fit the reported data very well. They suggest a different set of coefficients (as listed in Table I), which provide a better fit to the original data. These more accurate coefficients are much preferred over the classical values, and have been used in the example numerical model calculation in this paper. The collapse of microvasculature, a primary component of thermal burns in skin, was studied by Brown et al. in normal and several types of tumour tissues in 1992 [65].

Apoptosis and necrosis

Apoptosis, or programmed cell death, is widely thought to be one of the primary mechanisms in tumour response to hyperthermia [66], [67]. Other aspects of cell death result in autophagy and necrotic processes, some of which are also ‘programmed’ by a relatively newly identified pathway dubbed necroptosis [68], [69]. There are many extrinsic and intrinsic triggers for apoptosis and necrosis. Apparently, apoptosis and necroptosis are similar early on, in that they are both initiated by the tumour necrosis factor (TNF) cascade – receptor interactive proteins (RIP1, RIP3) with caspase result in apoptosis, while caspase-independent mechanisms result in necroptosis [68], [70]. Beyond supplying ATP, mitochondria also play a key role in cell death; they are intimately involved in the apoptosis protein cascade since they contain and release cytochrome c and apoptosis inducing factor [71]. Changes in mitochondrial permeability are observed in both apoptosis and necroptosis [72]. The multiple mechanisms, and pathways of these mechanisms, are presently under intense study because of their wide-ranging implications, and are substantially more complex than can be treated in this paper. To date, one study has provided kinetic coefficients for combined apoptosis and necrosis, as indicated by 2-3-5-triphenyltetrazolium chloride (TTC) vital stain studies in excised human prostate [73]. These results are particularly interesting since the low activation energy, E_a= 1.61 × 10⁵ (J mole⁻¹), and high critical temperature (94.2°C) indicate a relatively slow process not likely to be observed in relatively rapid heating, such as characterises laser sources. A recent study by McMillan [74] used nitro blue tetrazolium (NBT) in tonsil tissue. Several representative cell death processes are included in Table I. The example numerical model that concludes this paper illuminates these characteristics.

Measurement methods: Vital stain assays

Perhaps the most promising and ultimately most useful assays of thermal damage are the vital stains since they are applied directly to the tissue surface without sectioning or fixation – although gross sectioning is often required since their penetration depth is quite shallow. There are many vital stains – from acridine orange to the tetrazoliums – all with particular characteristics that prove useful in differing applications. Among them, the tetrazolium stains are interesting because they indicate viable cells for both cryosurgery [75] and heating [72], [73], [76]. NBT stains metabolically active tissues a brown-blue colour. It has the disadvantage that it must be cultured at 37°C, which sometimes indicates active cells that actually are not [72]. NBT stains were recently used to evaluate tonsil viability after laser irradiation in excised tissues [74]. In that work colour image analysis was used to precisely quantify the degree of damage, a promising approach that should give superior estimates of kinetic coefficients. TTC stains active tissues differing shades of red; and curing at room temperature reduces the frequency of false positives [72].

Laser multiple thermal damage process example calculation

An example numerical model illustrates the relative transient development of several of the damage processes listed in Table I. A Ho:YAG laser (λ = 2.09 µm) activation of 60 s followed by 40 s of cooling was implemented in a 101 × 51 node axisymmetric finite difference method (i.e. finite control volume) grid. The model space included equilibrium boiling at 1 atmosphere pressure – it also includes temperature- and water-dependent optical and thermal properties. The Ho:YAG wavelength is dominantly absorbed in water with an absorption coefficient of μ_a = 28 (cm⁻¹) in water [16]; and in the numerical model it was assumed that 80% of the total absorption was in tissue water (water = 55% concentration by mass) and 20% in residual (i.e. dry) tissue constituent proteins – as a result the effective tissue absorption coefficient was 19 (cm⁻¹). The generation term, Q_gen, for the energy balance was determined from:where w = the volume fraction of tissue water, Φ(0,0) is the beam centre surface fluence rate coupled to the tissue (W cm⁻²), and σ is the e⁻¹ beam radius (m).

The 10 mm diameter Gaussian profile beam (2σ diameter) had a total power of 1.1 W, resulting in a centre surface fluence rate of 2.8 (W cm⁻²) – i.e. a maximum adiabatic heating rate of 13.4 (°C s⁻¹). The tissue was 5 mm thick with convection and thermal radiation boundary conditions on both surfaces. The numerical model transient temperature results at the 1σ radius (2.5 mm) are summarised in Figure 2. Thermal damage predictions are summarised in Table II; the entries in the table are in sequence of maximum radius, with most sensitive at the top and least sensitive at the bottom. Additionally, the predicted levels of damage for the two transient record locations in Figure 2 are also included. The monotonic nature of the damage measures is clearly identifiable in the table. In this relatively short-term activation the apoptosis/necrosis damage process would not be observable since it lies within zones of much more severe anatomical and physiologic disruption. Most of the other cell death processes would be observable at the edge of the lesion as they lie outside of the predicted zone of micro-vascular disruption.

Figure 2. Transient temperatures at the 1σ radius (2.5 mm); at the surface (solid line) and at 2.5 mm depth (lower temperature dashed line).

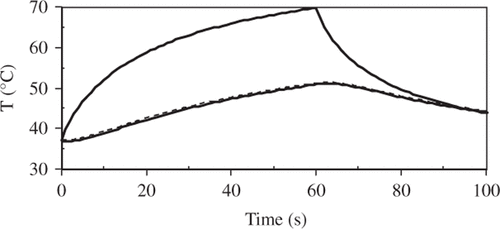
Table II.  Summary of damage model predictions for the Ho:YAG numerical model example.

	Radius (mm)			Depth (mm)		Damage for T(t) from Figure 2
Process	10%	90%	Δr (mm)	10%	90%	Surface	2.5 mm
CHO cells	5.2	4.4	0.8	Full	4.2	100%	100%
Murine embryoblasts	4.5	4.2	0.3	4.70	3.6	100%	100%
BhK cells	4.7	4.0	0.7	Full	3.4	100%	92%
μVascular	4.5	4.0	0.5	4.5	3.3	100%	88%
Skin burns	4.1	3.6	0.5	3.5	2.8	100%	18%
Muscle birefringence	3.9	3.2	0.7	3.3	2.3	100%	10%
SN12 cells	3.9	3.0	0.9	3.3	2.1	100%	8%
Collagen birefringence	3.1	2.4	0.7	2.1	1.5	70%	0.4%
Apoptosis/necrosis	3.5	2.1	1.4	2.7	1.3	55%	5%
Collagen shrinkage	2.7	1.7*	1.0	1.9	1.0*	40%	0

*Collagen shrinkage at maximum 60%.

Conclusions

The classical assessment method in hyperthermia studies, the thermal isoeffect dose, is an effective comparative parameter for long-term low temperature rise, irreversible thermal alterations, such as apoptosis and most probably necroptosis. However, it evaluates a single global measure of the thermal history, is comparative only, and not predictive of a particular outcome. It is also not particularly effective in describing and comparing higher temperature exposures [84].

In laser ablation and other similar higher temperature shorter-term heating, such as radio frequency current, there are multiple thermodynamically independent processes that will likely supersede or mask the classical markers of hyperthermia studies because they are more severe forms of thermal damage. Consequently, a single comparative parameter, such as thermal dose, cannot adequately describe the results. For these types of treatments more useful assessment methods that independently predict the extent of damage for multiple processes, both structural and physiological, are necessary. The Arrhenius absolute reaction rate kinetic model prediction of yield effectively fills that need since a virtually unlimited number of independent processes can be studied in parallel. The example numerical model calculation illustrates the relative contribution of each of the example processes to the overall result. Such an approach can facilitate the comparison of planned treatment regimens and aid in the design and development of new technologies at the higher temperatures.

Declaration of interest: This work was partially supported by the T.L.L. Temple Foundation (Lufkin, TX).

The author alone is responsible for the content and writing of the paper.