Could it be advantageous to tune the temperature controller during radiofrequency ablation? A feasibility study using theoretical models

Abstract

Purpose: To assess whether tailoring the Kp and Ki values of a proportional-integral (PI) controller during radiofrequency (RF) cardiac ablation could be advantageous from the point of view of the dynamic behaviour of the controller, in particular, whether control action could be speeded up and larger lesions obtained.

Methods: Theoretical models were built and solved by the finite element method. RF cardiac ablations were simulated with temperature controlled at 55°C. Specific PI controllers were implemented with Kp and Ki parameters adapted to cases with different tissue values (specific heat, thermal conductivity and electrical conductivity) electrode–tissue contact characteristics (insertion depth, cooling effect of circulating blood) and electrode characteristics (size, location and arrangement of the temperature sensor in the electrode).

Results: The lesion dimensions and T_max remained almost unchanged when the specific PI controller was used instead of one tuned for the standard case: T_max varied less than 1.9°C, lesion width less than 0.2 mm, and lesion depth less than 0.3 mm. As expected, we did observe a direct logical relationship between the response time of each controller and the transient value of electrode temperature.

Conclusion: The results suggest that a PI controller designed for a standard case (such as that described in this study), could offer benefits under different tissue conditions, electrode–tissue contact, and electrode characteristics.

• Ablation, cardiac ablation, closed loop control, finite element method, radiofrequency ablation, temperature controlled ablation, theoretical model

Introduction

Radiofrequency (RF) catheter ablation is currently used to treat some types of cardiac arrhythmias [1]. This technique uses RF current (≈500 kHz) to produce a thermal lesion and hence tissue necrosis in the target zone causing the arrhythmia. The electrical current is delivered to the tissue through a small active electrode placed at the tip of a percutaneous catheter, and a large dispersive electrode located on the patient's back. The most frequently used RF delivery protocol is temperature control [2], [3], which consists of modulating the applied RF voltage in order to keep the temperature measured in the active electrode approximately constant. The user sets the desired temperature value (target temperature) prior to ablation. The actual temperature of the active electrode is measured by means of a temperature sensor embedded at the tip. This modulating process is automatically performed by means of a controller inside the RF generator. Briefly, the controller uses an error signal to modulate the RF voltage, the error signal being the difference between the actual temperature and the target temperature.

The commercially available RF generators employ a proportional integral (PI) controller which is characterized by two parameters denominated Kp and Ki. The RF generator's Kp and Ki values are factory-set, i.e. these values cannot be programmed by the user. The value of these parameters therefore should, in theory, be selected with a view to obtaining good control action, i.e. to reach target temperature in a few seconds and keep it constant throughout the ablation. Certain factors are known to have an impact on lesion size, e.g. tissue characteristics [4], electrode–tissue contact characteristics [5–10], electrode size [10], arrangement [11–14] and position [15], [16] of the temperature sensor embedded in the electrode. Conversely, it is also known that varying these characteristics would affect the performance of the temperature control system. On this basis, it is important to quantify the sensitivity of the PI controller to parameter variation. To this end, the performance of a standard PI controller (i.e. designed for the standard case) is compared to that of specific PI controllers (i.e. those whose proportional and integral terms are designed for specific case values of the aforementioned factors). The quantitative magnitudes used for this comparison are the response time of the temperature control system, temperature deviation against a change in blood flow, and the estimated lesion size. It is important to point out that although other previous theoretical studies on RF cardiac ablation modelled feedback control systems as considered here, few have systematically evaluated the specific parameters Kp and Ki. Moreover, although we have extended our evaluation to different designs of RF ablation catheters, the used methodology could be equally valid to study more complicated electrode geometries.

Methods

Description of the theoretical model

Figure 1 shows the geometry and dimensions of the theoretical model, consisting of an active electrode placed perpendicular to the tissue surface, which implies a rotational symmetry axis and allows a two-dimensional model to be considered. The dispersive electrode is modelled as an electrical condition on boundaries at a distance from the active electrode, which is inserted into the tissue to depth P. We consider three P values: 0.75, 1.25 and 2.5 mm [10] as a first approximation for modelling different electrode-tissue pressure.

Figure 1. Two-dimensional theoretical model used. The active electrode tip is inserted into cardiac tissue with an insertion depth P. The dimensions R, Z and L are obtained by means of a sensitivity analysis.

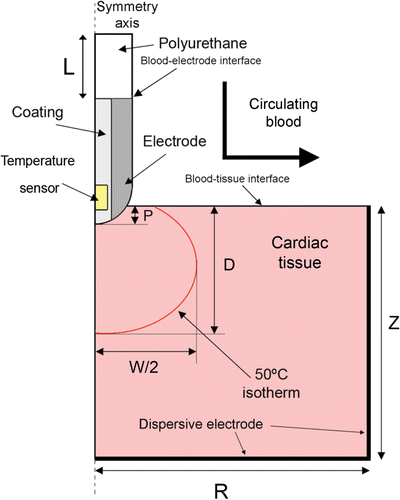
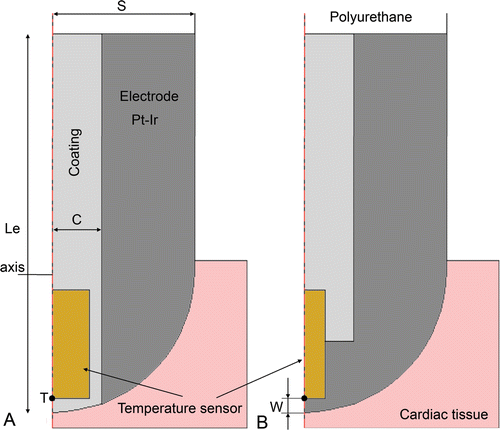
Since our study focuses on temperature-controlled RF ablation, the modelling of the temperature sensor in the electrode is crucial. In the clinical stage there are different arrangements. On one hand, the sensor can be placed in a crevice (visible on the electrode surface) with the metallic part completely covered by insulating material (Figure 2A). This arrangement allows tissue temperature to be accurately measured when the electrode is perpendicular to the tissue surface. Unfortunately it tends to underestimate tissue temperature when the electrode is parallel to the tissue surface, due to the cooling effect of circulating blood. Alternatively, the sensor can be totally embedded inside the electrode (with no apparent crevice) and in direct contact with the metal (Figure 2B). This arrangement provides the same accuracy in any relative electrode–tissue surface position, although the temperature is still slightly underestimated.

Figure 2. Detail of the two types of active electrodes considered the study. L_e is total electrode total length in (mm) and S is the electrode radius (in Fr), C is the layer of coating around the temperature sensor (C = 0.4 mm). The temperature sensor dimensions are 0.75 × 0.3 mm for type A, and 0.75 × 0.15 mm for type B. Point T indicates the place where temperature is assessed to implement the PI controller. The parameter w is the distance between location of P and electrode surface.

Governing equations and boundary conditions

From a mathematical point of view, the model is based on a coupled electric-thermal problem which was solved using the bioheat equation [17]:where T is temperature, t is time, ρ is tissue density, c is specific heat, k is thermal conductivity, q is the heat source produced by RF power, Q_p is the heat loss from blood perfusion and Q_m is metabolic heat generation. Q_p and Q_m are insignificant in RF cardiac ablation and thus were not considered [17]. The heat source q (Joule losses) is given by q = JE where J is the current density and E is the electric field strength. The electrical problem was solved using the Laplace equation where V is voltage and σ is electrical conductivity. The electric field is calculated by means of and J using Ohm law (J = σE). We used a quasi-static approach due to the frequencies used in RF ablation (≈500 kHz) and for the geometric area of interest the tissues can be considered as purely resistive [17].

Since blood circulating inside the cardiac chamber was not considered in the model domain, the blood–tissue interface and blood–electrode interface were really model boundaries (see Figure 1). The electrical boundary conditions were: zero current density in the transversal direction to the symmetry axis, blood–tissue interface and blood–electrode interface. A zero voltage boundary condition was set at the dispersive electrode. The initial voltage at the active electrode was 0 V. The voltage was then modulated to keep the sensor temperature more or less constant at point T in Figure 2.

The thermal boundary conditions were: null thermal flux in the transversal direction to the symmetry axis and constant temperature at the dispersive electrode and outer end of the plastic probe. The blood circulating inside the cardiac chamber produces a cooling effect on the tissue and electrode surfaces and was modelled by means of two thermal convection coefficients h_tissue and h_elec which represent the cooling effect at the blood–tissue interface and blood–electrode interface, respectively. We considered three blood flow rates: low, medium and high, which corresponded to three respective values for h_elec 721, 3636 and 5446 W/m²K and three for h_tissue 44, 708 and 1417 W/m²K [10]. Initial temperature was set at 37°C. Table I shows the values of the materials’ physical characteristics [7], [10]. The change in cardiac tissue electrical conductivity was +1.5%/°C [10] and in thermal conductivity of +0.001195 K⁻¹ [18]. We used COMSOL Multiphysics (COMSOL Inc., Burlington, MA, USA) to implement the numerical solution based on the finite element method. The dimensions R, Z and L (see Figure 1) were estimated by means of sensitivity analyses in order to avoid boundary effects. The value of the maximum temperature reached in the tissue (T_max) after 120 s of RF heating was used as a control parameter in these analyses. The mesh was heterogeneous, with a finer mesh around the electrode–tissue interface where the highest gradient was expected. The value of the parameters was increased by equal amounts in each simulation. When there was a difference of less than 0.5% between T_max and the same parameter in the previous simulation, we considered the former values as appropriate. The mesh was then refined to determine the appropriate spatial resolution. Likewise, we decreased the time-step to determine appropriate temporal resolution. In these sensitivity analyses, the applied RF voltage value was 16 V, which was chosen to keep T_max below 100°C [17]. Once the sensitivity analyses had been carried out, we solved the electrical–thermal problem with COMSOL and then we generated a FEM structure, which was exported to MATLAB (MathWorks, Natick, MA) to implement the PI control algorithm. Figure 3 shows the COMSOL-MATLAB interface in the model.

Figure 3. Interface between COMSOL and MATLAB in the model of temperature-controlled RF ablation. The electric–thermal coupled problem was solved by means of COMSOL, while MATLAB was used to implement the PI control algorithm.

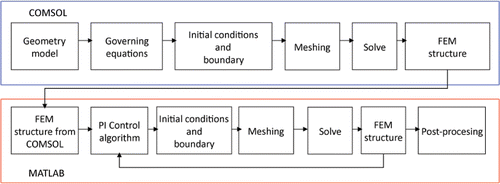
Table I.  Characteristics of the materials used in the model [7], [10].

Material	Region	σ (S/m)	ρ (kg/m^3)	c (J/kgK)	k (W/mK)
Cardiac tissue	Myocardial	0.541	1060	3111	0.531
Platinum-iridium	Electrode	4×10^6	21.5×10^3	132	71
Insulation	Coating	10^−5	32	835	0.038
Thermistor	Temperature sensor	10^−5	32	835	0.038
Polyurethane	Catheter body	10^−5	70	1045	0.026

σ, electric conductivity; ρ, density; c, specific heat; k, thermal conductivity. Tissue characteristics evaluated at 37°C.

Modelling of the PI control algorithm

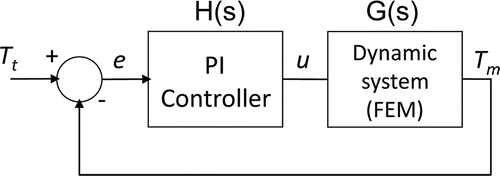
The temperature-controlled protocol is based on a temperature control loop located inside the RF generator (see Figure 4). The controller input is an error signal (e), which is the difference between the temperatures measured in the active electrode (T_m) and the target temperature set by the user (T_t). The controller uses this error signal to create a modulating signal (u), which modulates the voltage applied between the active and dispersive electrodes (output amplitude of a RF oscillator). Broadly, the control system has two subsystems: its own controller (i.e. an electronic system to keep the temperature measured in the sensor constant) and the modelled biological tissue. In the context of our study the biological tissue was considered to be a dynamic system, which has the modulating signal u as input, and the temperature measured in the active electrode T_m as output. Both subsystems have a response in terms of transfer functions, i.e. in terms of the relationship between the input and output signals. The transfer functions of the controller and the modelled biological tissue were H(s) and G(s) respectively (see Figure 5). The commercially available RF generators employ a PI (Proportional Integral) controller. In this case, the modulating signal u is the sum of two components:where K_p is the proportional constant, K_i is the integration constant, and e is the error signal [19]. The transfer function of the PI controller in Laplace-transformed quantities is described as:where, E(s) is the error, and U(s) is the controller output [19]. The design of parameters K_p and K_i is based on two steps: identification of the system response, and PI controller design.

Figure 4. Implementation of the temperature-controlled protocol inside the RF generator. The controller uses the error signal (e), which is the difference between the temperature measured at the electrode tip (T_m) and the target temperature set by the user. This signal is used by the PI controller to create an output signal (u) which modulates the output amplitude of a RF oscillator.

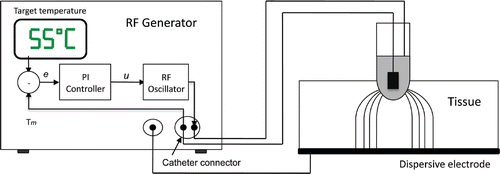
Figure 5. Block diagram of control system. The error signal e is the difference between the target temperature T_t and the temperature measured by the thermistor at the active electrode T_m. The applied voltage is modulated by means of the signal u. The dynamic system modelled by FEM includes the RF oscillator and the biological tissue.

Identification of the system response and PI controller design

The first step was to obtain an accurate identification of the modelled tissue's system response, which involves obtaining the transfer function G(s). This was done firstly by applying a constant voltage of 16 V for 300 s. The actuator was u(t) = V²(t) where V was the applied voltage. Once the temperature was stabilised around 55°C, a dynamic model was identified from the FEM temperature response. The identification was carried out using MATLAB. The accuracy parameter indicates the degree of similarity between plotted and transfer function. In our study this parameter was about 100, which demonstrated satisfactory identification. We used a second-order transfer function with one zero, as the obtained degree of identification accuracy was reasonable for the number of parameters being identified. Figure 5 shows the progress of the temperature measured in the active electrode obtained from the FEM simulation (real response) and those obtained from the transfer function (estimated response). The estimated transfer functions G(s) in Laplace-transform quantities had the form:where ΔT_m is the output and U(s) is the input of the dynamic system, A, B₁ and B₂ are the constant values identified, and k_S is the system gain. Once the transfer function was obtained, the values of parameters K_p and K_i were calculated by using root locus techniques [19]. With these values, the PI controller was used to model RF cardiac ablation in which the target temperature was 55°C and the duration was 120 s.

Note the PI controller in (2) and (3) represents a continuous time system. The designed controller was transformed into the discrete time (z domain) method in order to: (a) easily integrate the designed controller with COMSOL, and (b) obtain a simulation closer to actual ablation controllers, as all of them are implemented in discrete time.where T_S is the sampling period. The discretisation of (3) was carried out by Euler's forward method, as more elaborate methods, such as the Tustin (bilinear) transform lead to very similar discretized controllers when the sampling rate is much higher than the dynamics considered, as in our case.

Cases considered

Firstly, we designed a PI controller adapted to the tissue characteristics shown in Table 1, a 7 Fr and 4 mm electrode with 1.25 mm insertion depth, medium rate of blood flow, and a temperature sensor arrangement as shown in Figure 2A at a distance of w = 0.115 mm. This set of values represents the standard case. The associated PI controller designed from these values was denominated the standard PI controller. By varying these values we obtained different cases which can be classified into three groups: 1) cases considering the variations in tissue characteristics (specific heat, thermal conductivity and electrical conductivity) (see Table II); 2) cases considering variations in electrode–tissue characteristics, particularly in circulating blood flow and electrode insertion depth (see Table II); and 3) cases considering variations in the electrode design (see Table III), particularly in electrode size (diameter and length), arrangement of the temperature sensor (A and B as shown in Figure 2) and distance from the electrode surface (w).

Table II.  Description of the analysed cases including changes both in tissue characteristics [4] and electrode–tissue contact characteristics [10].

	Cases	Description
Variations in tissue characteristics	σ↑50%	Increase in electrical conductivity σ
	σ↓50%	Decrease in electrical conductivity σ
	k↑100%	Increase in thermal conductivity k
	k↓50%	Decrease in thermal conductivity k
	c↑100%	Increase in specific heat c
	c↓50%	Decrease in specific heat c
Variations in electrode-tissue contact characteristics	h↑	High rate of blood flow
	h↓	Low rate of blood flow
	P = 0.75 mm	Insertion depth of 0.75 mm
	P = 2.5 mm	Insertion depth of 2.5 mm

σ, electric conductivity; ρ, density; c, specific heat; k, thermal conductivity; h, thermal convection coefficient; P, insertion depth.

Table III.  Description of the analysed cases considering variation in the electrode characteristics [11–16].

	Ø (Fr)	Le (mm)	w (mm)	Type
Standard	7	4	0.115	A
Diameter	5	4	0.115	A
	8	4	0.115	A
Length	7	5	0.115	A
	7	8	0.115	A
Sensor arrangement	7	4	0.115	B
Sensor position	7	4	0.615	A
	7	4	0.615	B

Ø (Fr) is the electrode diameter, L_e (mm) is the electrode length, w (mm) is the sensor temperature position, electrode type (A or B, see Figure 2 for more details).

Conducted simulations and assessed parameters

Overall, we firstly analysed the behaviour of the standard PI controller for the cases described in the preceding section. We then repeated the analyses using the PI controllers specifically designed for each case. Finally, we compared both results for each case, i.e. standard PI controller versus specific PI controller.

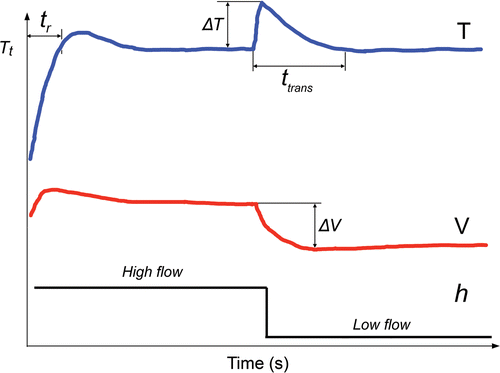
The specific case analyses included two types of simulations. In the first, all the parameters were constant throughout ablation (120 s) and the characteristics of the thermal lesion were assessed at 120 s: width W and depth D (see Figure 1) using the 50°C isotherm and maximum temperature reached in the tissue (T_max). In the second, a step change in the circulating blood flow (i.e. in coefficient h) was set at 60 s, i.e. once the electrode temperature was stable. Two changes were considered: low-to-high flow and vice versa. In the second simulation type, the following parameters were assessed (see Figure 6): (1) response time, or the time taken by the controller to reach target temperature (t_r); (2) maximum temperature variation measured in the active electrode (ΔT) after the step change in blood flow at 60 s; 3) maximum variation of applied voltage (ΔV) at that time; and 4) the transient time (t_trans).

Figure 6. Parameters used to study the dynamic response of each controller. The parameter t_r is the time taken to reach target temperature (T_t). Once a step change in blood flow occurs during the ablation, we considered the following parameters to define the behaviour of the controller: ΔT is the maximum variation of the temperature in the active electrode. ΔV is maximum variation of voltage applied by RF generator, and t_trans is the duration of the transient time needed to return to the target temperature. The step blood flow was modelled as a change in the thermal convection coefficient at the electrode–blood and tissue–blood interface.

Results

Characteristics of the theoretical models

From the sensitivity analyses, we obtained the following model dimensions: R = Z = 60 mm and L = 10 mm; a meshing size of 0.1 mm, and a time-step of 1 s. The models had about 6,000 nodes and simulations took around 20 min. Table IV shows the parameters K_p and K_i of the standard PI controller and of each specific PI controller.

Table IV.  The K_p and K_i parameters for the specific PI controllers.

Case	Kp	Ki		Kp	Ki
Standard	4.78	3.39	P = 0.75 mm	4.14	2.90
σ↑50%	2.43	3.70	P = 2.5 mm	3.94	5.00
σ↓50%	8.81	2.90	5 Fr-4 mm	5.95	2.48
k↑100%	5.38	2.30	8 Fr-4 mm	9.51	2.44
k↓50%	3.38	5.40	7 Fr-5 mm	10.20	3.15
c↑100%	5.04	4.50	7 Fr-8 mm	8.12	2.80
c↓50%	3.76	2.40	Type B 7 Fr-4 mm	17.28	5.96
h↑	4.67	3.20	Type A 7 Fr-4 mm w = 0.615	15.74	5.83
h↓	2.07	7.00	Type B 7 Fr-4 mm w = 0.615	28.58	7.33

Performance of the specific PI controllers in comparison to standard PI controller

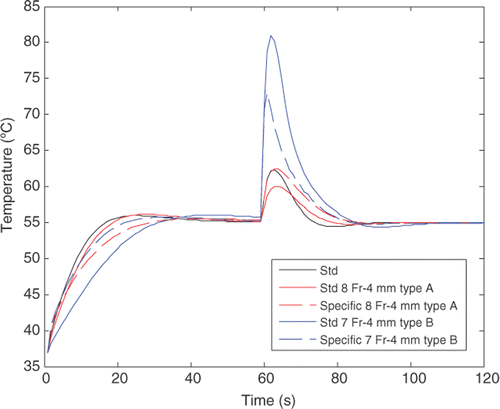
Table V shows the results obtained using the standard PI controllers and the specific PI controllers when tissue characteristics, electrode–tissue contact characteristics and electrode characteristics were varied. Note that the Std PI column shows the absolute values obtained, while the specific PI column shows the difference between the values obtained using the standard PI and specific PI controllers. The lesion dimensions (width and depth) and T_max remained almost unchanged when the specific PI controller replaced the standard PI controller: T_max varied less than 1.9°C, lesion width less than 0.2 mm, and lesion depth less than 0.3 mm. The results of the variation in response time do not reflect a clear tendency. In some cases the specific PI controller reduced this parameter by up to 7.7 s (7 Fr-4 mm Type A electrode with w = 0.615), but in other cases it was up to 12 s longer (case of k ↑100%).

Table V.  Results obtained using the standard PI controller (Std PI) and the specific PI controller when characteristics are changed (cases).

Standard case	Tmax (°C)		W (mm)		D (mm)		tr (s)
	66.2		6.8		4.9		15.4
	Tmax (°C)	ΔTmax (°C)	W (mm)	ΔW (mm)	D (mm)	ΔD (mm)	tr (s)	Δtr (s)
Other cases	Std PI	Specific PI	Std PI	Specific PI	Std PI	Specific PI	Std PI	Specific PI
σ↑50%	66.2	0.0	6.8	0.0	4.9	0.0	11.2	−1.7
σ↓50%	66.3	0.0	6.8	0.0	4.9	0.0	27.8	8.2
k↑100%	62.1	0.0	6.3	0.1	4.5	0.0	21.2	11.9
k↓50%	70.3	0.0	7.1	0.0	5.1	0.0	11.6	−3.8
c↑100%	65.9	0.0	6.5	0.1	4.5	0.0	16.3	−3.5
c↓50%	66.4	0.0	7.0	0.0	5.2	0.0	15.5	5.9
h↑	67.7	0.0	6.8	0.0	5.1	0.0	16.8	0.9
h↓	58.8	0.0	6.9	0.0	3.8	0.0	9.2	−3.7
P = 0.75 mm	67.2	0.0	5.8	0.0	4.6	0.0	16.0	2.4
P = 2.5 mm	62.2	0.0	7.5	0.0	4.7	0.0	12.8	−3.8
5 Fr-4 mm	62.3	0.0	4.6	0.0	3.3	0.0	13.5	6.5
8 Fr-4 mm	68.0	1.9	8.0	0.2	5.7	0.3	16.5	11.5
7 Fr-5 mm	67.0	0.0	7.0	0.0	5.0	0.0	16.0	4.0
7 Fr-8 mm	67.7	0.0	7.2	0.0	5.1	0.0	16.5	6.0
Type B 7 Fr-4 mm	100.1	0.0	11.6	0.1	7.9	0.1	26.0	−6.5
Type A 7 Fr-4 mm w = 0.615	101.0	0.0	11.6	0.0	8.0	0.0	26.5	−7.7
Type B 7 Fr-4 mm w = 0.615	103.5	0.9	12.0	0.1	8.2	0.1	27.0	−7.5

Std PI column shows the absolute values obtained, while specific PI column shows the difference between the values obtained using the standard PI controller and specific PI controller.

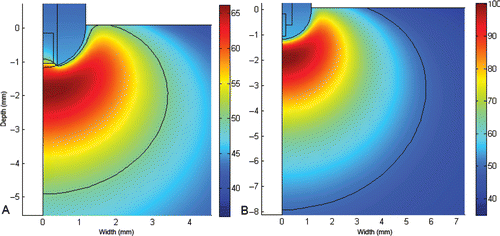
Figure 7 shows the temperature distributions in the cardiac tissue at 120 s using Types A and B electrodes (see Figure 2 for more details) with thermal lesion indicated by the 50°C isotherm. With the type B electrode, maximum temperature reached more than 100°C and produced larger lesions than Type A.

Figure 7. Temperature distributions in the cardiac tissue at 120 s (scale in °C) using the standard PI controller and the electrode type A and B (see Figure 2 for more details). The solid black line represents the 50°C isotherm (thermal lesion boundary). The lesion was 6.8 mm wide, 4.9 mm deep and maximum temperature was 66.2°C with type A, and 11.6 mm width, 7.9 mm depth and the maximum temperature of 100.1°C with type B.

Once more we did not find a clear tendency in the use of a specific controller instead of a standard controller regarding the dynamic performance of controllers when a step change in the circulating blood flow (coefficient h) was set at 60 s. As shown in Figure 8, in the case of the Type B-7 Fr-4 mm electrode, the specific controller produces less overheating (ΔT) than the standard controller (27°C versus 17°C), while the behaviour was exactly the opposite in the case of the Type A-8 Fr-4 mm electrode, i.e. the standard controller produces less overheating (4°C) than the specific controller (7°C). However, as predicted by linear dynamic system theory, we did observe a direct logical relationship between the response time (t_r) and the transient value of electrode temperature (ΔT), i.e. when the response time was increased (controller slows down), temperature increased. Likewise, the longer t_r, the longer the transient time (t_trans).

Figure 8. Evolution of the electrode temperature on different cases when a step of high-to-low blood flow occurred at 60 s.

Discussion

The aim of this study was to assess whether tailoring the Kp and K_i values of a PI controller during temperature-controlled RF cardiac ablation would be advantageous, in particular whether control action would be faster and lesion size larger. Computer simulations compared the performance of a standard PI controller and specific PI controllers adapted to different values, such as tissue characteristics, cooling effect of circulating blood, insertion depth of electrode into the tissue and electrode design. Although previous modelling studies had assessed the effect of tissue characteristics [4], insertion depth [6], [9], [11], blood flow rate [5], [8], [9], [11], electrode size [11] and temperature sensor arrangement [11–15] on the dimensions of the thermal lesion, some even including a PI controller in the modelling methodology [5], [6], [10], none had considered our hypothesis.

We are aware that some factors, such as tissue characteristics, cannot be known in advance, and therefore it would not be very useful to demonstrate that a specific PI controller adapted to a detailed set of specific heat, electrical and thermal conductivity values can improve control action. Future studies will be used to develop procedures to estimate the values of these characteristics in situ, and for this reason we included these factors in our study. In contrast, other factors are known in advance, such as those related to electrode design, or can be estimated in some way, such as insertion depth [20] and blood flow rate in the ablation zone [21]. Finally, the step change in parameter h considered in this study could model a situation where the electrode tip is steeply moved towards another zone with different blood flow cooling effects.

When we varied the parameters, the lesion sizes obtained were consistent with experimental results obtained in previous studies. For example, we found that an increase in electrode diameter caused an increase in lesion size; lesion width was 4.6, 6.8 and 8.0 mm for 4-mm electrodes of 5, 7 and 8 Fr respectively. Likewise, lesion depth was 3.3, 4.9 and 5.7 mm, which had been experimentally reported in previous studies [22]. A similar relation has been reported between electrode length and lesion size [23], as observed in our theoretical study: lesion width was 6.8, 7.0 and 7.2 for 7-Fr electrodes of 4, 5 and 8 mm respectively; and depth was 4.9, 5.0 and 5.1 mm. This agreement between our theoretical results and those obtained in previous experimental studies goes some way towards validating the proposed model. Moreover, our results indicate that the PI controller designed for the standard case is robust against variations in tissue characteristics, i.e. it allows action control to be conducted similarly in different cases.

The comparative results between specific and standard controllers (Table V) suggest that a PI controller designed for a standard case (such as that defined in this study), could be suitable under different conditions of tissue, electrode–tissue contact and electrode characteristics. In other words, the use of a specific controller with K_p and K_i values adapted to individual conditions causes almost no variations in lesion width and depth, as compared to a standard controller. Variations in response time (less than 12 s) were only found in some cases. This result only indicates that some specific PI controllers were not accurately designed, i.e. that other criteria could have been considered to reduce response time. In any case, these differences in response time do not seem to have an important clinical impact.

The direct relationship between response time (t_r) and the transient value of electrode temperature (ΔT) found in this study is logical, if we take the linear dynamic system theory into account. This result suggests that relatively fast controllers would be advantageous when large blood flow variations are expected.

Conclusions

The results suggest that a PI controller designed for a standard case (such as that described in this study), could be suitable under different conditions of tissue, electrode–tissue contact, and electrode characteristics, or, in other words, the use of a specific controller with K_p and K_i values adapted to individual conditions causes almost no variations in lesion width and depth, as compared to a standard controller. Only small variations with no clinical impact were found in response time in a small number of cases.

Declaration of interest: This work received financial support from the Spanish ‘Plan Nacional de I+D+I del Ministerio de Ciencia e Innovación’ Grant no. TEC2008-01369/TEC and FEDER Project MTM2010-14909. The translation of this paper was funded by the Universitat Politècnica de València, Spain. The authors alone are responsible for the content and writing of the paper