A feasibility study for non-invasive thermometry using non-linear ultrasound

Abstract

Purpose: High intensity focused ultrasound (HIFU) is used during hyperthermia cancer treatment to increase the tumour temperature. For an adequate and safe application it is important to measure the temperature in the heated region, preferably in a non-invasive manner and by the same modality as used for heating. The goal of this feasibility study is two-fold; first, it is investigated whether the acoustic non-linearity parameter B/A is most suitable for measuring temperature changes, second, a non-invasive thermometry method based on B/A is proposed and demonstrated.

Material and methods: Water is used to confirm that B/A is a sensitive acoustic medium parameter that is practically applicable for non-invasive thermometry. Next, a thermometry method is proposed that employs the ratios between the fundamental and the higher harmonic frequency components of a non-linear acoustic wave. The method determines these ratios for a measured acoustic pulse that has traversed a certain medium, and compares these with temperature dependent reference ratios for the same medium. The method is demonstrated using simulated measurements of an acoustic plane wave propagating in glycerol.

Results: Results obtained for water show that B/A is more sensitive for temperature changes than other practical acoustic parameters. For a combination of 16 simulated measurements, it is demonstrated that temperature can be predicted non-invasively with zero bias and a standard deviation of 2°C if the noise level does not exceed −40 dB.

Conclusion: The suitability of B/A as a basis for non-invasive thermometry is confirmed, and a non-invasive thermometry method based on B/A is proposed and successfully demonstrated.

• non-invasive thermometry
• non-linear ultrasound
• non-linearity parameter
• B/A
• HIFU

Introduction

Therapeutic heat is applied to cancer treatment, either as an adjuvant (e.g. hyperthermia) to other therapies (e.g. chemo or radiation therapies) [1–10] or as a stand-alone therapy (e.g. thermal ablation therapy) [11–15]. Although various methods exist to increase the tumour temperature, high intensity focused ultrasound (HIFU) is particularly interesting [16–19] in view of its focusing capabilities. With HIFU the intensity of the acoustic wave field increases to levels where its propagation is noticeably non-linear. This manifests itself in the time domain as distortion of the wave shape, and in the frequency domain as the formation of higher harmonic components, i.e. components with frequencies that are multiples of the frequencies of the source signal. The latter fact is significant for HIFU; absorption usually increases with frequency, and the occurrence of higher harmonics will cause dissipation to be larger than in the linear case [20]. The magnitude of the non-linear effects depends, among others, on the acoustic non-linearity parameter B/A of the medium [21], [22].

Before starting a HIFU treatment, it will be optimised by making a treatment plan. This involves the selection of the desired temperature profile and thermal energy flow [23], [24], and the determination of the required acoustic wave field. The latter step should ideally take into account the non-linear propagation of the field in an attenuative medium [25–29]. During the treatment it should be monitored whether the actual temperature increase in the tumour and the surrounding medium is according to the treatment plan. For both the patient and the clinician it is most convenient when this monitoring is done in a non-invasive manner. In the past, various methods have been investigated to achieve this goal: impedance tomography, active and passive microwave imaging, CT, as well as laser, infrared, magnetic resonance (MR), and ultrasound techniques [30]. In terms of logistics (instrumentation and operation) and costs it may be advantageous to pursue another goal: to use the same modality for treatment and monitoring. Both of these goals may be achieved with ultrasound, since sound waves may be used for both non-invasive hyperthermia and non-invasive thermometry [31]. In addition, ultrasound may be used for monitoring and control of the planned patient and applicator positions, which is an important issue as well [32].

To non-invasively monitor the temperature profile using ultrasound, in the region of interest the value of an acoustic medium parameter that is sensitive to temperature changes should be tracked in time. Provided that the temperature dependence of that parameter is known in advance, the distribution of its value may next be translated into a temperature map. Although this procedure may sound simple, the practical application involves many difficulties. Some issues that should be overcome are: finding a suitable acoustical medium parameter, developing a method to extract the parameter value from noisy measurements, finding the temperature dependence of the parameter for various types of biomedical tissues, eliminating or compensating the temperature dependence of other acoustical parameters, eliminating or compensating the influence of tissue inhomogeneities and gas bubbles, and achieving spatial selectivity.

Regarding the issue of finding a suitable acoustical medium parameter, it may be observed that several parameters have been proposed as a basis for non-invasive thermometry, such as the speed of sound, the acoustic absorption coefficient, the volume coefficient of thermal expansion, and the acoustic non-linearity parameter B/A. In the literature, many thermometry methods have been described that are based on the latter parameter. Most methods for the measurement of B/A extract this parameter from the pressure dependence of the speed of sound by employing an arrangement with a pump wave and a probe wave [33–38]. A different way of obtaining B/A is to consider the amplitude of the mixing components generated during the simultaneous propagation of two waves with different frequencies [39]. Still another method obtains B/A from the amplitude of the second harmonic [40], or the ratio between the second harmonic and the fundamental [41], [42]. Despite earlier interest in using B/A for thermometry, the question whether this is the most suitable parameter for this purpose still seems unanswered. The first goal of this paper is to quantitatively support the choice for B/A as a basis for non-invasive thermometry.

Regarding the issue of extracting the value of the relevant acoustic medium parameter from noisy measured data, it is observed that in the noise-free case the data contain redundancy. This fact may be employed to reduce the influence of noise. Therefore, the second goal of this paper is to formulate and demonstrate a non-invasive thermometry method that exploits redundancy for noise reduction.

To compare the suitability of different acoustic medium parameters as a basis for non-invasive thermometry, we need a medium with a well-known behaviour over a wide range of conditions. The best candidate for this is water; extensive data of the temperature dependence of acoustic medium parameters for biological tissues are not yet reported in literature. We will base our non-invasive thermometry method on non-linear acoustics, and we will use the redundancy between the higher harmonics to decrease the adverse influence of noise. The proposed method employs the ratios between the fundamental and the higher harmonics. For each measured acoustic pulse that has traversed a certain medium, these ratios are determined, and compared with the corresponding, temperature-dependent reference ratios for the same medium. This yields a prediction of the actual temperature of the medium. In this paper, we demonstrate the method by using simulated measurements of an acoustic plane wave propagating in glycerol. We use this material because of its increased tissue-like behaviour in comparison with water, and the fact that the temperature dependence of its acoustic parameters is well known. In the current context of a feasibility study, we restrict ourselves to a one-dimensional configuration with a homogeneous medium and a uniform temperature distribution. Issues such as compensating for the temperature dependence of other acoustical parameters, compensating for the influence of tissue inhomogeneities and gas bubbles, and achieving spatial selectivity, however important for the further development of the method, will currently be left unaddressed.

Theory and methods

We start by formulating the basic equation that describes the non-linear propagation of acoustic waves in biological tissue. Next, we show the cause of the temperature dependency of the acoustic non-linearity parameter B/A. Subsequently, we present a one-dimensional approximate method for the simulation of the non-linear acoustic wave field. Finally, we propose a non-invasive thermometry method which is based on the ratios between the various harmonic components that are present in the non-linear acoustic wave field.

Non-linear wave equation

The non-linear propagation of acoustic waves in biological tissue is well described by the Westervelt equation [43]. For a homogeneous, isotropic, lossless medium this equation readswhere is the acoustic pressure field, which depends on the spatial position and the time t. Further, c is the ambient speed of sound, ρ is the ambient volume density of mass, β is the coefficient of non-linearity, and and denote the volume density of volume force and the volume density of volume injection rate, respectively, of the sound source. The first term on the right hand side of Equation 1 is a non-linear term that represents the non-linear propagation of the acoustic wave. The non-linearity manifests itself by the formation of higher harmonic wave fields. The generation of higher harmonics depends, among others, on the coefficient of non-linearity. This coefficient may be written aswhere the A and B/2 are the first two coefficients in the Taylor series expansion of the equation of state for the medium under isentropic conditions [22].

Temperature dependency of the acoustic non-linearity parameter

Acoustic medium parameters such as the acoustic non-linearity parameter B/A are known to be temperature dependent. It has been shown by Beyer [44] that B/A may be divided intowhere is the speed of sound, α_T is the volume coefficient of thermal expansion, c_p is the specific heat at constant pressure, and T is the absolute temperature of the medium. Note that the subscript “0” will be used throughout the paper to indicate parameter values under ambient conditions. From Equation 3 it becomes clear that B/A consists of two contributions, of whichis based on isothermal pressure changes, whileis based on isobaric temperature changes. These terms can be understood as the relative increase in the phase velocity caused by variations in pressure (Equation 4), and temperature (Equation 5), see [44], [45].

Equation 3 clearly reveals the temperature dependency of B/A. The total effect of temperature changes on the formation of higher harmonics follows from the temperature dependence of the entire factor in the non-linear term in Equation 1, and also involves the temperature behaviour of ρ and c.

Simulation of non-linear acoustic waves with the Burgers equation

The development of our method for measuring the temperature of a medium necessitates that we can simulate the non-linear propagation of acoustic waves for different values of B/A. In the current context we prefer to perform this with the one-dimensional, forward wave method based on the equation derived by Burgers [46]. This equation may be obtained from the one-dimensional, lossless and source-free Westervelt equation, and provides the simplest method to compute non-linear wave propagation. The Burgers equation readswith retarded time and spatial coordinate x [22]. This equation has the implicit solutionwhere the spatial step size Δx must be small enough to yield only a small variation in the pressure . A full derivation of the employed solution method is given by Huijssen [27].

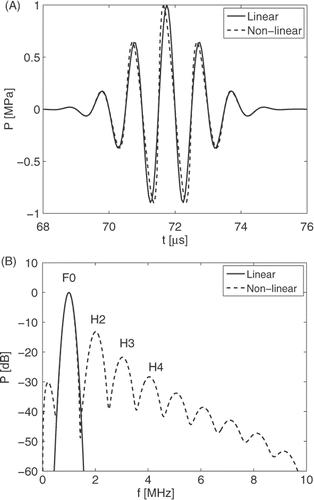
As an example, we may use Equation 7 to compute the propagation of a one-dimensional, pulsed, acoustic wave in water at T = 35°C (ρ = 994 kg m⁻³, c = 1520 m s⁻¹, β = 3.7). At the source, the pressure pulse is a Gaussian modulated pulse that equalswith source pressure amplitude P₀ = 1.0 MPa, centre frequency f₀ = 1 MHz, time delay , and envelope width . In Figure 1, the time domain and frequency domain results for non-linear propagation of the wave over a distance of x = 0.1 m are shown and compared with the results for linear propagation. In the time domain, the non-linear behaviour causes a steepening of the up-going parts of the wave shape. In the frequency domain, this manifests itself through the generation of the higher harmonics H2, H3, H4, etc., in addition to the fundamental spectrum F0. Moreover, the non-linear behaviour causes a self-demodulated signal at frequencies below F0 [22]. The magnitude of the observed non-linear phenomena will depend on the value of the acoustic non-linearity parameter B/A, and will thus change with the temperature of the medium.

Figure 1. Comparison between a linear and a non-linear pulsed, plane acoustic wave. The waves propagate in water and are evaluated at a propagation distance x = 0.1 m; (A) temporal results, (B) spectral results. The non-linear waves are obtained by using the solution of the Burgers equation.

The thermometry method that we will propose in the next section will be applicable to both pulsed and (quasi) steady-state wave fields. In situations where the (quasi) steady-state wave field of the HIFU applicator is used for heating, it is efficient to employ a frequency domain solution of the Burgers equation [47]. However, in situations where a pulsed wave field is used for heating, a time domain approach is preferable. In this paper we will consider the latter.

Non-invasive thermometry based on non-linearity

In the previous sections we have made plausible that the acoustic non-linearity parameter B/A is temperature dependent and that variations in temperature affect the non-linear propagation of the acoustic wave. In particular, the amplitudes Hi of the i^th harmonic component of the non-linear acoustic wave field depend on the value of B/A. In the Results section below we will show that this dependence on B/A is different for each i. A general approach to determine temperature profiles during HIFU treatment is to reconstruct an acoustic medium parameter from measured data of the scattered acoustic field, and to relate the local values of the parameter to the local temperatures. To employ non-linearity for non-invasive thermometry, this would require a method to solve the Westervelt equation for known measured data of the pressure field and the unknown parameter B/A, or more precisely, the unknown factor . In practice, this means that a non-linear scheme is needed to invert the Westervelt equation. Approaches as formulated for linear acoustics [48] are not expected to work due to the ill-posedness of the problem. Hence, we propose a pragmatic method for the extraction of B/A, or in fact the temperature, from measured acoustic field data.

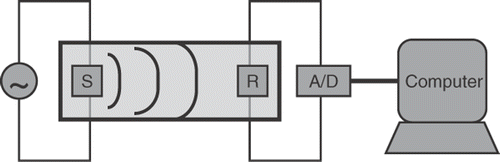
To explain our method, we consider a one-dimensional configuration for transmission-mode measurements in a homogeneous medium at a constant and uniform temperature. A schematic overview of this configuration is shown in Figure 2. In this configuration a fixed source S is generating a prescribed pressure pulse, which travels towards receiver R. First we simulate the non-linear acoustic wave field for a given propagation distance x, over a range of temperatures. From this we obtain a set of reference ratios , each of which is defined as the ratio between the amplitudes of the i^th and the j^th harmonic component. The reference ratios are equal toThese temperature-dependent ratios are stored for later use.

Figure 2. The one-dimensional transmission-mode set-up used for demonstrating the non-invasive thermometry method. An electric pulse drives a submerged acoustic transducer S which generates an acoustic wave field. The non-linearly propagating field is measured with a receiver R. The received analogue signal is converted via an A/D converter and recorded by the computer for further signal processing.

Next, for an as yet unknown temperature, the non-linear wave field at the propagation distance x is measured. From this we obtain a set of measured ratios . Relating a measured ratio to the corresponding reference ratio delivers us, from each ratio, a temperature prediction T_i,_j. The separate temperature predictions will differ due to the noise in the measured data. By averaging the temperature predictions for the different ratios, we obtain a prediction for the temperature of the medium. We may further improve the result by averaging the values of obtained from multiple measurements.

Results

We first present the acoustic non-linearity parameter B/A for water as a function of temperature, and we explain why this parameter is a good candidate to measure temperature. Next, we show simulations of the acoustic wave field in glycerol at various temperatures, as obtained with the solution of the Burgers equation. Finally, for the one-dimensional case, we demonstrate the prediction of the temperature of a medium from simulated noisy data.

Temperature dependency of the acoustic non-linearity parameter

As a consequence of Equation 3, a quantitative examination of the temperature dependency of the acoustic non-linearity parameter B/A requires knowing the behaviour of the volume density of mass ρ, the volume coefficient of thermal expansion α_T, and the specific heat c_p, as a function of temperature T and for a given ambient pressure p₀. We limit our temperature range of interest to T = [20°C, 70°C], although in some applications temperature increases above 70°C occur. For the ambient atmospheric pressure we take p₀ = 0.1 MPa. Since we want to assess the temperature behaviour of as many acoustic parameters as possible, at this stage we consider the most studied liquid, i.e. water, as testing medium. In Figure 3 we present , , , and in addition . The latter is the temperature-dependent coefficient for square power law acoustic absorption, which is typical for water; most biological tissues show frequency power law absorption with an exponent between 1 and 2. The functions in Figure 3 are obtained by interpolating a set of values that have been measured at p₀ = 0.1 MPa and over the temperature range T = [0°C, 100°C], as reported in [49–51]. Moreover, Equation 3 requires a model of , i.e. the speed of sound as a function of both temperature and pressure. Various models are based on least square curve fitting of a polynomial function to a set of measurement values. The most well-known are from Belogol'skii et al. [52], whose model is only valid up to T = 40°C, and from Bilaniuk and Wong [53], whose model is only valid at p₀ = 0.1 MPa. Unfortunately, the temperature range of the first model is lower than the temperature range we are interested in, while the second model does not yield any pressure dependence. Therefore, we use the less well-known model developed by Wilson [51], which is based on measurements over the temperature range T = [0.9°C, 91.2°C] and the pressure range p = [0.1 MPa, 96 MPa]. This is the same model as used by Beyer [44] to compute B/A for a limited number of temperatures. The resulting speed of sound as a function of temperature and pressure is shown in Figure 4. The results clearly reveal that over the given temperature and pressure ranges, the changes in the speed of sound are dominated by variations in temperature. 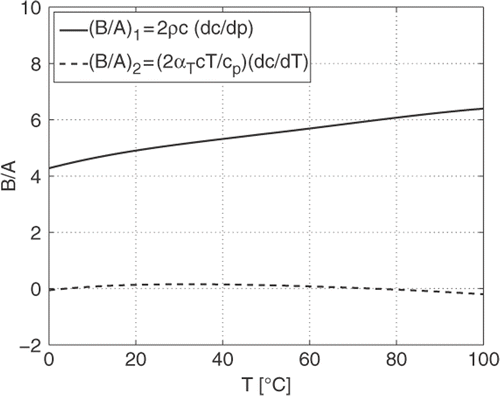Next, we compute the gradient of the speed of sound function along the pressure axis to obtain (B/A)₁ for isothermal pressure changes, and along the temperature axis to obtain (B/A)₂ for isobaric temperature changes. The results are shown in Figure 5. Note that the contributions to B/A from the isothermal temperature changes are much higher than the contributions from the isobaric pressure changes.

Figure 3. Acoustic medium parameters of water as a function of temperature, at ambient pressure; (A) specific heat c_p, (B) volume density of mass ρ, (C) volume coefficient of thermal expansion α_T, (D) acoustic absorption coefficient . Continuous results (solid lines) are obtained by interpolating discrete values (dots). The values are obtained from Lide, Spickler et al., and Wilson [49–51].

Figure 4. The speed of sound of water as a function of pressure and temperature. The values are obtained from the model by Wilson [51].

Figure 5. The contributions to the acoustic non-linearity parameter B/A of water arising from isothermal pressure changes and isobaric temperature changes, at ambient pressure.

Combining (B/A)₁ and (B/A)₂ results in the required acoustic non-linearity parameter B/A as a function of temperature and pressure, see Figure 6. In this figure we compare our computed values for B/A with the results obtained by Beyer [44] and Hagelberg et al. [54]. These authors computed their results in the same way as we computed ours, using data measured by Wilson [51] and Holton [55], respectively. Our results are in close agreement with Beyer's results, which is expected since the underlying model for is identical. The deviation between our results and those of Hagelberg may entirely be attributed to the difference in the employed model.

Figure 6. The computed acoustic non-linearity parameter B/A of water at ambient pressure, compared with values obtained by Beyer [44] and Hagelberg et al. [54].

In order to compare the sensitivity of the acoustic medium parameters for temperature changes, we present the behaviour of B/A, c, ρ, α_T, , and c_p in one graph, see Figure 7. Note that, prior to starting hyperthermia treatment with HIFU, the temperature of the tumour and the surrounding tissue is known. Hence, only the temperature increase in the region of interest is of importance and should be measured. Consequently, it is more relevant to investigate the relative change of a medium parameter as a function of temperature than its absolute value. Therefore, in Figure 7 we have used the reference temperature T₀ = 37°C. For numerical comparison, in Table I we present the relative change of each mentioned parameter over the temperature intervals T = [37°C, 42°C] and T = [37°C, 70°C].

Figure 7. The relative changes of the parameters B/A, c, ρ, , , and c_p of water. The reference temperature is T = 37°C at ambient pressure.

Table I.  The relative changes of the parameters B/A, c, ρ, α_T, , and c_p when T increases from 37°C to 42°C and from 37°C to 70°C, for water.

Parameter	Value			% change
	T = 37°C	T = 42°C	T = 70°C	37°C → 42°C	37°C → 70°C
B/A (computed)	5.41	5.50	5.91	1.6%	9.1%
c	1524 m/s	1532 m/s	1555 m/s	0.6%	2.0%
ρ	993.3 kg/m^3	991.4 kg/m^3	977.8 kg/m^3	−0.2%	−1.6%
1 + ΔT αT	1.000	1.002	1.012	0.2%	1.2%
αa/f ^2	1.35 · 10^−16 s^2/cm	1.26 · 10^−16 s^2/cm	0.70 · 10^−16 s^2/cm	−6.9%	−48.3%
cp	4178 J/(kg K)	4179 J/(kg K)	4190 J/(kg K)	0.005%	0.264%

The results in Figure 7 clearly show that the acoustic absorption coefficient is the most sensitive to temperature changes. The second most sensitive is the acoustic non-linearity parameter B/A, which in turn is at least four times more sensitive to changes in temperature than the speed of sound c, the volume density of mass ρ, the volume coefficient of thermal expansion α_T, and the specific heat c_p. In practice is hard to measure because it is difficult to distinguish absorption from scattering effects. Consequently, B/A could be more favourable for non-invasive thermometry. Note that these results are based on water, whereas the results might vary between different types of tissue.

Simulation of non-linear acoustic waves with the Burgers equation

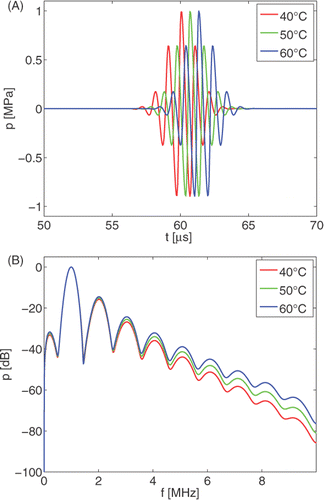
The results presented in the previous section demonstrate the temperature dependency of the acoustic medium parameters that occur in the non-linear acoustic wave equation. The influence of temperature on the non-linear propagation of an acoustic wave may most easily be demonstrated for a one-dimensional acoustic wave in a homogeneous and lossless medium. In Figure 8 we show the results of one-dimensional acoustic wave simulations that are based on the Burgers equation. This figure displays both the temporal and the spectral content of waves that have propagated over a distance of x = 0.1 m in glycerol, at three different temperatures, i.e. T = (40°C, 50°C, 60°C). In the time domain (Figure 8A), variation of the temperature manifests itself in both a temporal shift and a change of the wave form, and in the frequency domain (Figure 8B), temperature variations cause a change in the amplitudes of the harmonic components and the phase of the signal (not shown). The applied acoustic medium parameters of glycerol have been obtained from Sehgal et al. [56]. The wave shape that has been emitted at x = 0 m is a Gaussian modulated pulse with amplitude P₀ = 1.0 MPa, centre frequency of 1 MHz, time delay , and envelope width .

Figure 8. Plane acoustic wave at a propagation distance x = 0.1 m in glycerol at temperatures T = 40°C, 50°C, 60°C; (A) temporal results, (B) spectral results, normalised with respect to the fundamental F₀.

Non-invasive thermometry based on non-linearity

To demonstrate the performance of our non-invasive thermometry method, we consider a simulated pulsed acoustic plane wave that propagates over a distance of 0.1 m in glycerol. We use glycerol because of its increased tissue-like behaviour in comparison with water, and the fact that the temperature dependence of its acoustic parameters is well known.

First we compute the reference ratios . We employ the known temperature behaviour of the acoustic parameters of glycerol in the solution of the Burgers equation, and compute the acoustic pulses at x = 0.1 m and for different temperatures T. After subjecting these pulses to a Discrete Fourier Transformation (DFT), the maxima Hi of the harmonic frequency bands are determined, and these are used to compute the reference ratios as a function of temperature.

Next, we simulate a single measurement. The temperature of the glycerol is assumed to be T = 40°C, which is the temperature to be reconstructed. The solution of the Burgers equation is used once more to compute the corresponding acoustic pulse at x = 0.1 m. To mimic measurement circumstances, we add 1% (−40 dB) white noise to the obtained pulse. In Figure 9A we present the time domain data for a single simulated measurement, and in Figure 9B we show the frequency spectrum of this data. The latter plot is obtained by subjecting the simulated measurement data to a discrete Fourier transformation.

Figure 9. Simulated measurement data for a plane acoustic wave in glycerol, as computed with the solution of the Burgers equation and contaminated with 1% white noise; (A) temporal results, (B) spectral results for several different situations.

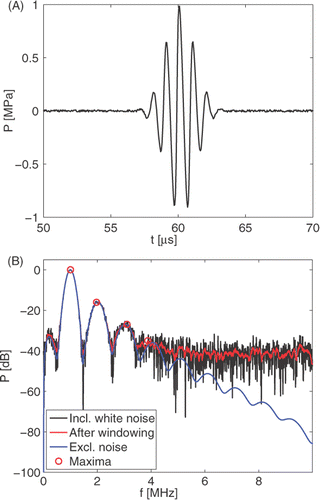
Subsequently, we determine the simulated measured ratios from the maxima of the frequency spectrum. From Figure 9B it may be expected that the spectrum of the simulated measurement is too noisy to yield accurate maxima for the third and higher harmonics. To overcome this problem we first process the spectrum by averaging over a moving window of four spectral points. This gives a considerably smoother spectrum, which is also shown in Figure 9B. This smoothed spectrum is used to determine the maxima of the harmonic frequency bands, and these maxima are applied to determine the steepening measured ratios .

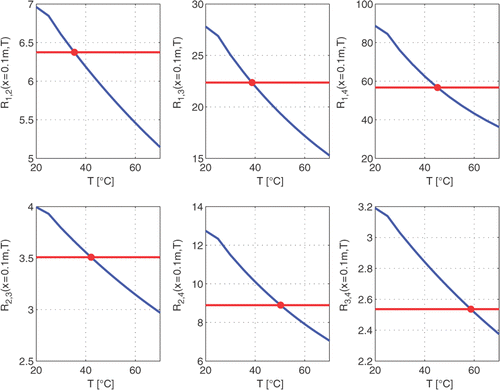
The above comes together in Figure 10. In this figure, we use blue lines to display the reference ratios involving the fundamental, second, third, and fourth harmonic, i.e. R_1,2, R_1,3, R_2,3, R_1,4, R_2,4, and R_3,4, as a function of temperature. In the same figure, the horizontal red lines indicate the simulated measured ratios , as obtained from the simulated measurement shown in Figure 9. By finding the intersection point of the blue and the red lines, we obtain a temperature prediction based on one ratio.

Figure 10. Comparison of the temperature dependent reference ratios (blue lines) and the measurement ratios obtained from the simulated measurement data (red lines). The simulated measured ratios are obtained from the single simulated measurement in Figure 9.

The temperature predictions of different ratios will in general differ due to the noise in the measurement. Unweighted averaging of these predictions provides us with a temperature prediction based on combined ratios of the single simulated measurement, see Figure 11. Here we have introduced the notation , where μ is the mean and σ the standard deviation of the averaged predictions. The results for the predicted temperature are shown in Table II. These results show that an increase in accuracy is achieved when we use not only R_1,2, but also ratios involving the third harmonic component, i.e. R_1,3 and R_2,3. However, when we also use the ratios involving the fourth harmonic, i.e. R_1,4, R_2,4 and R_3,4, this leads to a worsening of the result. The reason of this is that the fourth harmonic is very small and severely disturbed by the noise, such that even the window averaging over four spectral points results in a very inaccurate location and magnitude of the maximum of the fourth harmonic frequency band. This makes that all measured ratios involving this fourth harmonic are inaccurate, which results in a bad overall result.

Figure 11. Prediction of the temperature from the single simulated measurement in Figure 9; (A) employing the fundamental, second and third harmonic, (B) employing the fundamental, second, third and fourth harmonic. The blue dots indicate the temperature obtained from the comparison of the individual simulated measurement and reference ratios. The red stars give the average temperature, and the red lines show the standard deviation.

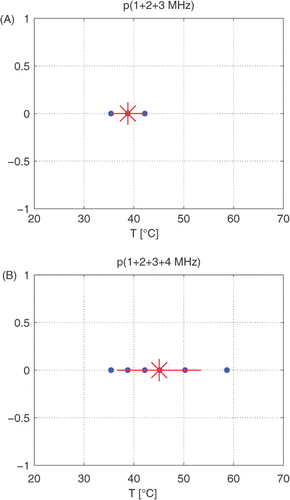
Table II.  Predicted temperatures from simulated measurements in glycerol. The temperature to be reconstructed is T = 40°C. In the notation , μ is the mean and σ the standard deviation of the averaged predictions.

Ratios involved	Single simulated measurement	16 simulated measurements
R1,2	35°C	40 ± 2°C
R1,2, R1,3, R2,3	39 ± 3°C	44 ± 3°C
R1,2, R1,3, R2,3, R1,4, R2,4, R3,4	45 ± 8°C	–

In realistic situations, temperature prediction need not be based on a single measurement, but may involve several measurements in fast succession. Hence, we repeat the simulated measurement 16 times and average the obtained temperature predictions. The results of the average temperatures are shown in Table II. Temperature prediction including the ratios involving the fourth harmonic did not succeed due to the adverse effects of the noise in some realisations of the simulated measurement.

Discussion

Non-linear acoustics play an important role in HIFU. The most noticeable effects of non-linear acoustics, as compared to linear acoustics, are an increase in dissipation [57] and a spatial shift of the region with maximum dissipation toward the transducer [58]. Both phenomena are caused by the conversion of a part of the acoustic energy from the fundamental component towards the higher harmonic components, which in most tissues have a higher attenuation rate. An additional effect of the application of HIFU for thermal ablation therapy is the formation of bubbles and cavitation [59]. These bubbles and cavitation may form a barrier for the acoustic wave field where energy may scatter off, and form an additional source of non-linearity that causes an enhanced conversion towards higher harmonics, and in turn, an enhancement of tissue damage and a further shift of the peak of maximum energy deposition [60]. Consequently, the actual location and magnitude of maximum temperature increase may differ significantly from a traditional treatment planning that is based on linear acoustics. On the one hand, the difficulty of making an accurate treatment planning with the traditional linear tools shows the necessity for accurate (and preferably non-invasive) thermometry during treatment. Even when the treatment planning is being based on non-linear acoustics, the restricted knowledge about tissue boundaries and tissue behaviour, and the formation of bubbles and cavitation, will lead to uncertainties that call for thermometry during treatment. On the other hand, as this paper confirms, the acoustic non-linearity parameter B/A is very sensitive to the temperature changes [44], [45], [61] and may be the best choice as a basis for non-invasive thermometry. A practical issue that needs to be overcome is the restricted quantitative knowledge about the temperature dependency of B/A (and other relevant acoustic parameters) for many biological tissues. Another issue that may arise is that the behaviour of a specific type of tissue may vary between individuals or even within one individual. These difficulties may be somewhat relieved by the fact that the temperature before treatment is known, and only the temperature changes need to be monitored. Yet another potential issue is that tissue properties such as B/A may change irreversibly as a result of the treatment. Fortunately, this problem is virtually absent for the relatively low temperature rise that occurs with hyperthermia, which is the therapy that is most dependent on an accurate thermometry. On the other hand, during thermal ablation therapy the formation of regions with ablated tissue, bubbles and cavitation may complicate non-invasive thermometry that is based on (non-linear) acoustics, as in these regions the acoustic medium parameters will change irreversibly and most often significantly. However, with this therapy accurate thermometry is less important than precise localisation of the treatment zone. In view of the latter, irreversible parameter changes might even prove valuable, as they can be used to clearly localise those regions where the temperature increase has had a significant impact.

A characteristic feature of non-linear acoustics is the formation of higher harmonics during the propagation of the acoustic wave field. The ratios of these harmonics depend on the acoustic non-linearity parameter B/A, and are therefore temperature dependent. Our proposed non-invasive thermometry method is based on the various ratios measured in transmission-mode between the fundamental and the higher harmonic components that are present in measured data. If no noise is present, each harmonic ratio will give the same temperature prediction, and the exact temperature may be predicted from a single ratio. In other words, the temperature information provided by the different ratios is redundant. Figure 8B implies that ratios of harmonics that are spectrally further apart are more sensitive to temperature changes. However, in the presence of noise, the maxima of the harmonic frequency bands may deviate from their exact noiseless values. As a result, different ratios will yield different temperature predictions, and the prediction from a single ratio will likely contain some error. By averaging the predictions from a number of ratios, the observed redundancy may be employed to reduce the adverse effect of noise. As long as the applied ratios are related to harmonics that clearly stand out above the noise, this will in general improve the temperature prediction. However, when ratios are used that involve noisy harmonics, the prediction may turn worse. Clearly, there is an optimum in the number of harmonics that should be included in the prediction, and this number depends on the level of the harmonics relative to the noise level.

To investigate the performance of the proposed thermometry method, we have used simulated measurement data for a one-dimensional acoustic wave that propagates in glycerol at T = 40°C. To mimic measurement circumstances, the data was contaminated with 1% (−40 dB) white noise. Although it is difficult to find specific data for the noise in practical ultrasound systems, the applied signal-to-noise ratio (SNR) seems on the small side, and it is expected that many modern ultrasound systems actually have a larger SNR. This implies that our thermometry method might yield more accurate results than demonstrated in this paper.

Predicting the temperature from a single simulated measurement by using the reference and simulated measured ratios involving up to the second harmonic yields a temperature  = 35°C, including up to the third harmonic gives , and including up to the fourth harmonic gives . The differences between the predicted temperature and the real temperature (biases) are for the respective cases. In realistic situations, temperature prediction will be based on several measurements. Averaging the predicted temperatures from 16 simulated measurements yields when only the ratio involving the fundamental and the second harmonic is applied, and when all ratios involving the fundamental, second harmonic, and third harmonic are applied. Now the differences between the predicted temperature and the real temperature are for the respective cases. Temperature prediction including the ratios involving the fourth harmonic as well was unsuccessful due to the adverse effects of the noise in some realisations of the simulated measurement. Both the predictions based on a single simulated measurement and on a series of simulated measurements demonstrate that there is an optimum in the number of harmonics that should be taken into account.

The presented method uses only the local maxima of the harmonic frequency bands. This makes the approach rather sensitive to noise in the data, as the results demonstrate, while at the same time it disregards a large amount of data available for free. By better using the information that is present in the noisy frequency spectrum of the measurements [62], the overall accuracy and sensitivity in the presence of noise may be improved.

In a clinical setting, it is very important to achieve spatial selectivity (besides knowing the temperature dependence of the acoustic medium parameters related to the relevant tissues, and having a way to deal with significant scattering and refraction caused by bubbles, cavitation and tissue inhomogeneities). Regarding this aspect, it may be advantageous that HIFU systems are particularly suited to deposit the emitted acoustic energy in a small volume inside the body. As a result, the magnitude of the acoustic wave field, and thus the non-linear effects, inside this volume are significantly larger than outside. This may help to provide the required spatial selectivity for non-invasive thermometry.

Conclusion

In this paper we have confirmed that the acoustic non-linearity parameter B/A is very sensitive to temperature changes and that it may be the best choice as a basis for non-invasive thermometry. Moreover, we have presented a non-invasive thermometry method that is based on the use of B/A. This method predicts the temperature by comparing the harmonic ratios from a measured and a reference non-linear acoustic wave field. To counter the adverse effects of noise, redundancy is applied by averaging the predictions from different ratios of a single measurement, and by averaging the predictions from several measurements. Simulations have been performed with a pulsed acoustic plane wave that propagates over a distance of 0.1 m in glycerol. The results show that by combining 16 simulated measurements, the temperature can be predicted with zero bias and a standard deviation of 2°C if the noise level does not exceed −40 dB.

Acknowledgement

The authors would like to thank Eldert Both from Delft University of Technology for his contribution to this work.

Declaration of interest: The authors report no conflicts of interest. The authors alone are responsible for the content and writing of the paper.