Model-based planning and real-time predictive control for laser-induced thermal therapy

Abstract

In this article, the major idea and mathematical aspects of model-based planning and real-time predictive control for laser-induced thermal therapy (LITT) are presented. In particular, a computational framework and its major components developed by authors in recent years are reviewed. The framework provides the backbone for not only treatment planning but also real-time surgical monitoring and control with a focus on MR thermometry enabled predictive control and applications to image-guided LITT, or MRgLITT. Although this computational framework is designed for LITT in treating prostate cancer, it is further applicable to other thermal therapies in focal lesions induced by radio-frequency (RF), microwave and high-intensity-focused ultrasound (HIFU). Moreover, the model-based dynamic closed-loop predictive control algorithms in the framework, facilitated by the coupling of mathematical modelling and computer simulation with real-time imaging feedback, has great potential to enable a novel methodology in thermal medicine. Such technology could dramatically increase treatment efficacy and reduce morbidity.

• bioheat transfer
• MR temperature imaging
• real-time control
• finite element modelling
• laser-induced thermal therapy

Introduction

Minimally invasive image-guided ablation of focal cancerous lesions is becoming a more prevalent alternative to conventional surgical interventions for patients who are not ideal surgical candidates [1]. Significant interest in computer-assisted prospective planning [2] and real-time thermal delivery control [3] has been generated by active clinical research in image-guided thermal therapy procedures. The increasingly powerful computational and visualisation resources continually becoming available suggests that the role of the computational sciences will continue to escalate in image-guided thermal therapy procedures.

In this article, major components of a computational framework that provide the backbone for both treatment planning and real-time surgical monitoring and control are reviewed. A unique and innovative aspect of the framework is model-based predictive control focused on applications to image-guided laser therapy. Although the computational framework is designed for LITT in treating prostate cancer, it is further applicable to other thermal therapies in focal lesions induced by radio-frequency (RF), microwave and high-intensity focused ultrasound (HIFU). We first review the mathematical modelling aspects in LITT. The main ideas include the bioheat transfer model coupling with laser–tissue interaction, laser applicator cooling and thermal dose models. The computational framework and its major components are discussed next, followed by discussion on tissue heterogeneity, uncertainty quantification and real-time control. Finally, the generality of the framework and future directions are discussed.

Mathematical modelling aspects

Bioheat transfer models

The effectiveness of LITT relies on the accurate control and placement of laser probe(s). Realistic modelling of the phenomena of thermal energy deposition and heat transfer in biological tissues is dependent on accurate modelling of both the bioheat transfer and tissue response to thermal energy induced by various thermal treatment modalities (e.g. laser, RF, HiFU, etc.). The tissue-domain geometry adds to the complexity and may be represented by an arbitrary shape embedded with complex blood vessel structures. In order to simplify the problem, some forms of homogenisation are typically assumed so that tissues can be considered as a continuum at the macro-level. In many cases, the micro-level information is lost during this process. However, it is important to model heterogeneity resulting from different thermal material properties [4] in different parts of the tissue domain. In addition, these tissue properties may depend on temperature itself, resulting constitutive (material) nonlinearities and time dependency due to, e.g. blood coagulation. Other factors such as the cooling effect of vascularised tissue may need additional consideration (e.g. fluid dynamics) in order to account for blood flow and accurate characterisation of perfusion.

Pennes bioheat transfer model

Because of the availability of constitutive parameters and relative ease of computer implementation, the Pennes bioheat transfer model [5] is commonly used for modelling the temperature field, u(x, t). This model is based on the conservation of energy analysis applied to a tissue mass of interest, which yields a time-dependent partial differential equation (PDE) describing the transfer rate of thermal energy through a blood perfused biological domain, Ω. Equation (1) is a generalised version of Pennes equation that includes temperature and spatial dependency in thermal properties and convection effect of blood. Note that the temperature is denoted as u throughout this manuscript, rather than T. Let , n = 2 or 3 denoting two- or three-space dimension.

Here the initial temperature u₀(x) is typically assumed as 37°C. The specific heat of tissue and blood is denoted as, c_t and c_blood, respectively. ρ is the density of tissue, u_a is the measured core body temperature that manifests in a nearby artery and k(u, x) is the spatially- and temperature-dependent thermal conductivity. By examining each term in Equation (1), the value of perfusion, ω(u, x), is dimensionally equivalent to a volumetric mass flow rate of blood through the tissue, kg/s/m³. It is important to distinguish the blood perfusion from the spatially-dependent velocity, v(x). The blood perfusion represents a blood flow through a porous tissue media. Velocity v(x) represents a potential source of convective heat transfer due to either a large vessel or an active cooling fluid about a thermal delivery applicator. At a position x in the domain, it is assumed that either v(x) or ω(u, x) is non-zero, but not both. This is a necessary assumption for Equation (1) to be mathematically well defined. However, velocity and perfusion can be zero at the same time in some cases (e.g. for intestinal content). Regarding model parameters, values for the perfusion, thermal conductivity, density and specific heat may be obtained from tabulated handbooks; values for the flow velocity may be measured or obtained from a coupled Navier–Stokes model of the fluid flow [6].

Boundary conditions for the Dirichlet, Neumann and Cauchy types are defined on , and , respectively, which are assumed to be known. For LITT simulations, the Dirichlet boundary condition, u_D(x), may be used to model an active cooling fluid flowing about the applicator (Section ‘Laser–tissue interaction’). Conditions defined on the Neumann boundary may be used to prescribe a known heat flux, , or used to impose a symmetrical heat distribution about the boundary plane, g_N(x) = 0. Cauchy boundary condition may be used to model the heat exchange of the tissue with the ambient atmosphere, u_∞, and h is the heat transfer coefficient.

Numerical solutions of the Pennes bioheat equation are amenable to finite difference [7] and finite-element [8] techniques with implicit [9] and explicit [10] time-stepping schemes. The classical Courant stability condition for the time step must be observed for explicit schemes. It is important to note that the addition of the convective term, v(x), typically requires some additional form of numerical stabilisation techniques such as streamline upwind Petrov–Galerkin, Galerkin least squares or multi-scale methods [11–13].

Other bioheat transfer models

Bioheat transfer processes in living tissues are often influenced by blood perfusion through the vascular network. When there is a significant difference between the temperature of the blood and the tissue through which it flows, convective heat transport will occur, altering the temperatures of both blood and tissues. This effect will most likely be significant during hyperthermia therapy or thermal ablation treatment when large vessels are present nearby or in the region to be treated.

Although Pennes bioheat transfer model is commonly used, the characterisation of the perfusion term in the model has often been debated. Other bioheat transfer models have been proposed over the years based on various assumptions. Equation (1) is, in fact, a generalised version of the original Pennes equation. However, it depends on the accurate description of spatial- and temperature-dependent k(u, x) and ω(u, x), which can be obtained by inverse analysis based on the availability of in vivo temperature measurements such as MR thermometry.

To account for thermal effects due to large vessels in the tissue, Charny's three-equation model [14] is built upon a coupled system of artery, vein and surrounding tissue. Roemer's tissue-convective energy balance equation model [15] includes eight approximations to the so-called exact equation. An early study to model bioheat transfer with vascular structures was proposed by Chen-Holmes [16]. It was shown that the major heat transfer process occur in the 50–500 µm diameter vessels, not the capillary beds. Thus, their results refuted Pennes’ assumption. The concept of thermal equilibrium length was introduced and two additional terms were amended to Pennes model to account for this effect. Weinbaum and Jiji conducted theoretical and experimental studies on bioheat transfer effect of vascular microstructure on surface tissue [17], [18] and introduced a model with local blood perfusion. More recently, Deuflhard and Hochmuth [19] investigated bioheat transfer with the consideration of micro vascular system, in which the first- and second-order correction terms to Pennes equation were introduced based on multi-scale and homogenisation idea with an assumption that microstructures are periodical. Based on volume averaging technique, two groups (Nakayama et al. and Shrivastava et al.) introduced independently a generic bioheat model that accounts for blood flow effect [20], [21]. It is worth mentioning that vascular bleed-off may be one of the other attributes in bioheat transfer process. For the discussion of other bioheat transfer models, we refer to, e.g. [22] and references therein.

With the advance of imaging modalities such as MRI, CT and angiography, it is possible to represent the geometry and domain of interest more accurately. However, a general comprehensive biophysics-based bioheat transfer model, which can utilise rich anatomical imaging data produced by various imaging modalities, are still in need.

Modelling uncertainties

Uncertainty quantification has become a very active research field in computational science due to increasing computing power and demand for more realistic computer model predictions. Here, we focus only on some aspect of uncertainty associated with temperature prediction based on bioheat transfer modelling. It is well known that a potential repercussion for modelling the bioheat transfer in greater biological detail is the requirement of more constitutive parameters. In most cases, these parameters cannot be measured directly. They can only be estimated within a range or described with a probability distribution. On the other hand, computer models formulated and solved in a stochastic sense are rapidly becoming standard tools in the simulation of natural phenomena. For instance, a stochastic differential equation form of Pennes bioheat model has been considered and applied to RF ablation [23]. A probability density function (PDF) was used to represent uncertainties in modelling parameters such as perfusion and thermal conductivity. Additional methods of uncertainty quantification are available, including polynomial chaos [24], [25] and Markov Chain Monte Carlo [26] methods. These techniques in uncertainty quantification and propagation may deliver more informative solutions with confidence intervals but at a substantially increased computational cost.

Laser–tissue interaction

Several methods can be used for modelling laser and thermal tissue interaction. Numerical solutions to the unsimplified integral–differential radiant transport equation (RTE) [27] utilise the least assumptions and provide the most flexibility in terms of applications. The standard diffusion approximation characterises the diffuse radiance at position x propagating in direction ω (Note that this is not the same as the perfusion ω(u, x)) as the first two terms of a Legendre polynomial series expansion.

Here ϕ_d is the diffuse fluence rate and j is the radiant flux. This equation was discussed at length in [28]. With standard diffusion approximation, explicit analytical solutions to the RTE are available for simple geometries. Explicit analytical representations of spherically symmetric solutions to the RTE require relatively simple implementation and may be used to model an interstitial laser source with certain accuracy [28]. The following expression can be used as the source term in Pennes or other bioheat transfer models at any point in the tissue.

where P(t)[W] is the laser power as a function of time emitted from the point source, μ_a [1/cm] and μ_s [1/cm] are the absorption and scattering coefficients, respectively. The anisotropic factor is denoted as g, and x₀ is the position of laser photon source. Also, this expression of the point source may be utilised as a basis for modelling the fluence from a finite volume diffusing laser tip.

For any laser source with fluence emitting from a finite volume (part of the domain), the total thermal energy delivered to the system needs to be integrated over the entire domain except for the laser tip. Let P*[W/m³] be a power density emitted from the volume and provides a fluence that is conformal with the applicator geometry [2], [30]. Then, the total fluence is of the form

This representation may be guided by the discretisation of the computational domain, Ω, but does not explicitly require distinct computational domains for tissue and applicator, Ω_tip.

Analytical representations of the fluence are also available for external laser fibres [31], [32]. However, explicit analytical solutions are not as compact and require evaluations of a cylindrically symmetric solution cast in terms of Bessel functions. Additional flexibility in modelling spatially- and temperature-dependent optical parameters is provided at an increase in computational cost by solving the underlying RTE numerically as a system of equations coupled with the bioheat transfer model. The underlying PDE to be solved is typically a simplified form of the integral–differential radiant transport equation [33], [34].

The irradiance, E, and direction of the applied source, , are assumed to be known in each particular application. On the boundary, n is normal to the surface and n is the refraction index. Upon computing the diffuse fluence, ϕ_d, the biological heating is proportional to the sum of the scattered and unscattered light, Q_source = μ_a(φ_d + E). Additionally, a so-called δ–P approximations may relax the diffusion theory assumptions, μ_a << μ_a(1 − g), and model the light scatter in a preferential forward direction [31].

The altered form of the phase function in the δ – P approximations manifests as modified coefficients in the underlying governing equation for the fluence with f = g²,  = μ_s(l − f), and . The assumption is that μ_a << μ_a(1 − f) is valid.

Laser applicator and cooling model

For safety reasons, the control of the maximum temperature near the applicator tip is very important. If the temperature is too high, tissue is charred near the laser tip so that photons can no longer penetrate. It would result in rapid localised heating that can damage the applicator and even leave melted residual portions of the applicator remaining in the tissue. One of the solutions is to provide an applicator with active cooling by running coolant at ambient temperatures through designed channels surrounding the applicator depicted in Figure 1. As noted, it is crucial to prevent tissue charring close to the delivery site [35].

Figure 1. Illustration of relative position of laser applicator with respect to the digital representation of a prostate (left) and detailed model of the active cooling achieved by a coolant running at ambient temperature around a photon emitting diffusing laser tip (right).

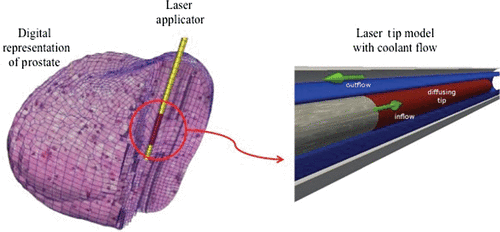
There are several possibilities for modelling the cooling effect. One approach is to manipulate the thermal conductivity and to mimic rapid heat dissipation [36] by artificially increased k near the applicator. Also, Dirichlet boundary conditions can be used [30], [37] as effective cooling. However, neither of these approaches is able to accurately capture the physics of the cooling fluid heated as thermal energy carried away from the delivery site via convection. The third approach is to model the cooling applicator explicitly and take into account the convective transport of the cooling fluid [38] in addition to add a convective term in Equation (1). However, this will increase the modelling complexity tremendously, especially for finite-element mesh generation near the applicator. When utilising the implicitly structured mesh inherent to the MR imaging obtained for planning purposes with that mesh, unintended meshing discretisation artefacts can arise from under-resolved regions of the applicator near the interface to the tissue.

Nonetheless, an explicit domain of elements for the applicator is ideal, but requires significant additional mesh generation effort. Analytical solutions for the cooling temperature within the applicator are desirable for reducing any discretization error, and can also be integrated into the numerical model very easily.

Cell damage model

Another important component in modelling MRgLITT is how to evaluate cell and tissue damage under therapeutic thermal conditions. Cell damage based on Arrhenius models are typically used [39] for that purpose. Introduced in 1947 [40], [41], the idea to quantify thermal damage, specifically for tissue, was based on a first-order chemical reaction rate proposed by Arrhenius [42] to characterise pathological transformation from one state to another.

The assumption is that the rate of cell damage is proportional to exp(−E_a/Ru), where E_a is the activation energy, R the universal gas constant and u the absolute temperature. However, Arrhenius type of damage models suffer from its inability to predict cellular injury over a wide hyperthermic temperature range and throughout the entire heating process, its hyper sensitivity to small changes in parameters (particularly frequency factor) and the ambiguity in interpretation of model parameters characterising the cell damage formulation.

Available experimental data (e.g. [43]) suggest that there may be two transitional temperatures around 43°C and 52°C in the temperature range from 39°C to 60°C. A different injury mechanism may be initiated at each of these temperatures. To accommodate the data pattern, we may use piecewise function, e.g. two or multiple separate Arrhenius model to cover two regions, which is not mathematically elegant and lacks physical insight.

To overcome the weaknesses of the Arrhenius model described above, other types of models have been proposed for thermal damage of cells and tissues. These include models are based on statistical methods [44], enzyme denaturation [45], thermal dose model [46] and other more general kinetic theory. For a discussion of various cell damage models, He and Bischof [47] provide a comprehensive review. Most of these models, however, relate thermal damage to the rate process in such a way that the rate of change with respect to temperature and time are decoupled.

In a recent study [48], a two-state model built upon in vitro cell viability experiments was derived using simple arguments motivated by classical statistical thermodynamics. This model characterises two populations of viable (live) and damaged (dead) cells, which leads to the damaged cell population of the form, C(u, t) = exp(−ΔG/ku)/(l + exp(−ΔG/ku), or alternatively, , where C(u, t) is a function of both temperature and time; k is the Boltzmann constant and ΔG is interpreted as a change in a functional analogous to a classical Gibbs free energy, depending on both temperature and exposure time. To determine ΔG, cell viability data from in vitro experiments with human prostate cancerous (PC3) and normal (RWPE-1) cells were used to calibrate the two-state cell damage model derived in this study. As compared to the Arrhenius model, the two-state model captures the damage process more accurately over a wide hyperthermic temperature ranges, including the beginning phase when cells are first exposed to the heat. Also, the model is able to characterise the sigmoidal behaviour of the cell response. To serve as control criteria in MRgLITT, either Arrhenius or two-state cell damage models can be used depending on available model parameters.

Computational framework and its major components

To construct a model-based real-time control system, it is crucial to derive models and algorithms that are both computationally accurate and efficient. The accuracy is delivered by building patient-specific model that faithfully represents the domain of interest, and governing equation that contains realistic model parameters. As long as MR thermometry (i.e. MR Temperature Imaging (MRTI)) data (Figure 2) are available, patient-specific model parameters can be derived by inverse analysis [49]. The computational efficiency at the real-time level is usually achieved by either implementing parallel algorithms or reduced models that may sacrifice accuracy.

Figure 2. MRTI-driven computational framework: core modules include bioheat transfer inverse bioheat transfer, and patient-specific models. On the left of the flow chart, laser parameters and MRI/MRTI data were input to the bioheat transfer model that will be validated. The middle section of the flow chart illustrates how the optimal laser parameters are obtained based on patient-specific data during the treatment. The right side of the flow chart depicts the decision-making process based on predicted treatment out comes. The framework supports quantifiable decision-making for treatment planning and real-time surgical monitoring and control.

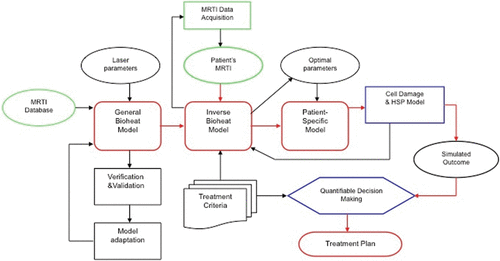
Major components of the framework [49], [50] include data acquisition, geometry extraction, mesh generation, registration, model calibration, laser parameter optimisation, prediction and visualisation. In the following, we review major steps in these components.

Image processing

The raw imaging data are often of poor quality that makes it difficult to build a quality meshed model of the anatomy under investigation. In order to improve the image quality, a suite of image-processing functionalities is used. (1) Contrast Enhancement – improving the contrast of the image to help extraction of the domain of interest, (2) Filtering – removing the noise by modifying the input image using bilateral filtering coupled with an anisotropic geometric diffusion PDE. (3) Segmentation – dissecting an image into anatomically separate regions of interest using fast marching method so that each region can be extracted from the raw image. (4) Image Skeletonisation – extracting lower dimensional features from the image by analysing the critical points of the imaging data. (5) Flexible Alignment – performing affine transformation to best fit an image of a biological system onto a different instance of the same. This process was described in more detail in [50].

Geometry processing

After imaging process, the geometry of interest needs to be extracted via following steps: (1) Surface Extraction – geometry extraction from the imaging data is either done using contouring, or by reconstructing a piecewise triangulated or higher order surface model from the boundary voxels of the segmented regions. (2) Curation/Filtering – the initial surface model extracted from the imaging data has topological anomalies, namely small components, spurious noisy features etc. The algorithms developed to resolve the model of such anomalies include point cloud regularisation and volumetric primal and dual space feature quantification. (3) Segmentation – geometric segmentation of an initial model often leads to better understanding of the quality of the model in terms of its topology n-dimensional geometry. A distance function induced by the geometry can be used as a criterion. (4) Skeletonisation – the skeletal feature of a model provides a lower dimensional description of a geometry in building further meshed models of the anatomy that was utilised. A Skeletonisation algorithm extracts a polylinear or polygonal skeletal structure from the geometric model and further assists in annotating the shape into tubular or flat regions. More details can be found in [50].

Patient-specific model generation

The patient-specific model generation process starts with aligning a sequence of two-dimensional anatomical MR images and rendering them into a three-dimensional (3D) geometry that represents patient's disease region or regions. The next step is to generate a computational mesh with good quality based on this 3D object. The LBIE Meshing tool (cvcweb.ices.utexas.edu/cvc) and Cubit software (cubit.sandia.gov) are available. Both permit patient-specific finite-element mesh generation of the biological domain using pre-operative MRI data. The task of meshing is primarily divided into two parts – boundary element and volumetric element. Each part has three sub-modules depending on whether the resulting mesh is linear or higher order. For boundary element meshing there are three options: triangle/quadrilateral meshing, B-spline meshing and A-spline meshing. Similarly, for volumetric element meshing there are also three different meshing modules: tetrahedra/hexahedral meshing, solid NURBS meshing and A-spline meshing.

Laser power optimisation

Before a treatment, the location of laser probe and laser power are optimised according to the thermal damage zone prescribed by a surgeon. The initial optimisation is to minimise the difference between desirable temperature profile and predicted temperature filed, which will result in probe location and laser power profile. In fact, the computational framework is capable to optimise other laser parameters (e.g. frequency) or tissue properties (e.g. effective thermal or optical properties). Initial optimisation is to provide the best possible setup for laser surgery by providing a surgeon with information for positioning the laser probe and initial laser power setting.

Model calibration during laser therapy

During treatment, intra-operative MRI data is used to register the computational domain with the biological domain. Real-time thermal imaging (MRTI) data drive the calibrations aligning the parameters of the bioheat transfer model to reflect patient's biological tissue values. As new thermal imaging data are acquired intermittently, the computational prediction is compared to the measurements of the real-time thermal images. Using the difference as the quantitative measure of error (defined in some norm), the laser parameter set is optimised in real-time and new laser device setting is adjusted according to the prediction. In the previous experiments [50], imaging data were transferring from an MRI scanner at M.D. Anderson Cancer Center (MDACC) in Houston, TX, to the computing facilities at Texas Advanced Computing Center (TACC) in Austin, TX, over GigE Internet connection.

Real-time control and remote visualisation

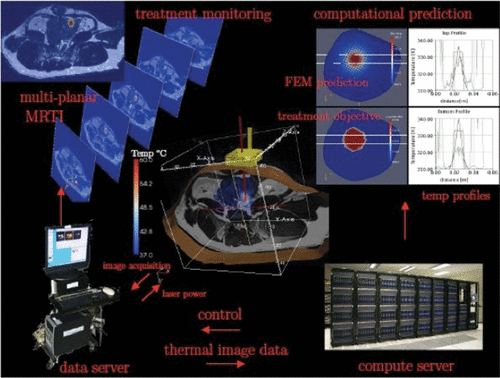
Thermal images received by the computing facilities in Austin provided the raw data for real-time control algorithm that implicitly regulates the power wattage output and profile of the laser applicator in Houston. The parallel optimisation implementation is built from the PETSc [51] parallel computing paradigm and the Toolkit for Advance Optimisation (TAO) [52] parallel optimisation library. Advanced Visualisation Studio (AVS) [53] is used in conjunction with a Virtual Network Computing (VNC) server for remote visualisation. AVS co-routines are used to manage and coordinate the simultaneous visualisation of the MRI anatomical images, MRTI thermal images and finite- element data sets (Figure 3).

Figure 3. An Illustration of work flow for model-based real-time control of laser therapy. Based on the pre-operative MRI scan and initial optimisation, the laser probe is place to the specified location. During the treatment, multi-planar MRTI scans are acquired for monitoring. These data are also used to calibrate the computational model to reach a preset tolerance of accuracy before a predictive control sequence starts. The control parameters optimised in real-time using supercomputers are transmitted to the data server that controls the laser probe. Both computational (FEM) model prediction and treatment objective are display on the screens in the operative room.

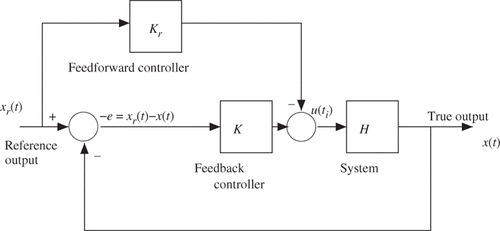
Tissue heterogeneity and model-based predictive real-time control

The development of fast proton resonance frequency (PRF) shift-based temperature imaging [54] provided profound opportunities in control of the thermal dose delivery. PRF is one of the fundamental properties of a material, which can be measured under magnetic resonance (MR) scan. Using PRF-shift, particularly phase shift, in vivo temperature measurement can be achieved since the constant increment is observed with respect to temperature change per unit degree. PRF-based imaging provides a quantitative 3D temperature field that can be exploited as feedback for a variety of delivery modalities. Substantial work in controller development has been done for MR-guided focused ultrasound (MRgFUS) that is applicable for MRgLITT in control of the bioheat transfer. Initial feasibility studies show that the thermal dose delivery can be formulated within a rigorous optimal control linear-quadratic regulator framework [55]. A natural choice of control variable is to track the error between a desired temperature and the measured temperature. Based on numerical simulations, a proportional controller [56] was shown capable of achieving a thermal dose distribution that conformed to the target. Also, numerical simulations can be used to study the control performance based on the solutions of the bioheat transfer equation. Moreover, controller design needs to adjust laser power adaptively in proportion to the detected difference between the measurements and desired temperature. Further investigation is necessary to extend the feedback paradigm to the proportional-integral-derivative (PID) control regime [3]. In addition to using the difference between the measured and desired temperature, PID controller can also employ the derivative and the integral of the error in the control decision to mitigate overshoot and steady state error, respectively. Within the PID control regime, the error and its integral can be measured by comparing MRTI to the desired temperature value. The derivative is estimated by incorporating the Pennes bioheat transfer model, which tightly couples with the control framework. The predictions of the temperature state will determine the best strategy to control the system dynamics in the presence of modelling uncertainty.

The feasibility of developing an adaptive model-based feedback control system that uses dynamic multi-planar MRI temperature measurements in response to the delivery of the prescribed thermal dose in real-time has been demonstrated during MRgLITT [8]. In this study, real-time MRTI (5 slices every 5 seconds) was acquired during therapy delivery at the imaging laboratory at MDACC and transferred to a massively parallel supercomputer system at TACC. The optimal laser power was obtained to design treatment protocol, which was simply to create a lesion utilising a temperature history of 60°C within the 1.2 cm diameter sphere. A two-stage protocol was used in the preliminary control system. A non-damaging location finding laser pulse was used to provide low-temperature heating with real-time MRTI driving the update of the computational bioheat transfer model parameters to generate a patient-specific model. The optimal power modulation was then computed and delivered to create the desired lesion to conclude the treatment. The difference between delivered therapy in terms of temperature and model prediction was <5°C at the peak.

The initial feasibility studies were developed within a model-based feedforward algorithm, PDE constrained optimisation problem framework and each phase of the protocol was accompanied by a preset dead-time to allow for computations to reach a solution. Furthermore, feedback was used only in the calibration phase and consequently, the full scale of thermal imaging data were available but not all were utilised for the sake of efficiency. This technique can be further developed to fully exploit the continual interaction between the patient (system), laser power (input) and thermal imaging monitoring (feedback). A systematic range of controller structures needs to be further investigated through alternatively formulated clinically relevant cost function definitions and several control domains including stochastic optimal control [57], adaptive control [58], and robust control [59], [60]. These will include optimising the developed controllers to achieve the desired clinically relevant tradeoffs between performance of the transient and steady state thermal response as well as desired robustness characteristics.

The computational complexities, accuracy and performance of a range of control scenarios must also be thoroughly investigated. Peak performance massively parallel computing approaches require algorithms that evolve with the latest memory and floating-point computing architectures. In addition to highly parallelised computational approaches, model reduction approaches have also been suggested [61]. While model reduction approaches can drastically reduce the computational expense, validating the accuracy of the model reduction solution approximation for clinically relevant scenarios presents an additional complexity.

Basically, there are two methods to design a control system. One approach is to use a continual feedback designed to track a pre-computed, but uncalibrated, trajectory [62], as opposed to the other approach using purely feedforward control with calibration [8]. Of course, one may use intermediate control approaches, which can be designed to employ a partially calibrated feedforward trajectory with intermittent feedback (Figure 4). To achieve patient-specific realtime control, however, we need to design a precise time sequence based on execution of high-speed data acquisition and transfer, imaging registration and mesh generation, high-performance computing for numerical solutions, efficient inverse analysis algorithms for optimisation, fast-response laser applicator based on model prediction. More details can be found in [49], [50].

Figure 4. A tracking control system will combine the predictive patient specific feedforward modelling capabilities with feedback control to provide control decisions u(t) that force the state x(t) to conform to an ideal temperature state x(t).

Conclusions

Model-based real-time predictive control offers great potential for computer-assisted surgery. Although the computational framework reviewed in this article focuses on the laser ablation, it could be equally applicable, in the future, to other ablation therapies using RF, microwave or HIFU with minor modifications and added modules for the heat source. The framework is also applicable to hyperthermia and cryotherapy. The major advantage of the framework is its modularised implementation so that new therapeutic modalities can be integrated into the framework. The major components discussed here provide the backbone for not only treatment planning but also real-time surgical monitoring and control. It is shown that the predictive control based on MR thermometry and applications to image-guided LITT or MRgLITT is very effective. Parallel to the advances in computational science and computer technology, we expect the model-based real-time control to be widely adopted in medical practice and provide a viable surgical tools with controllable treatment outcome.

Acknowledgements

We would like to thank the entire Dynamic Data Driven Application System (DDDAS) team sponsored by NSF/CNS-0540033, which was led by Drs J. Tinsley Oden, Kenneth Diller and John Hazle; and consisted of other faculty and participating graduate students who are listed in [50]. This work carried on by authors is partly sponsored by NIH/5K25CA116291-05 (YS), NSF/HRD-0932339 (YF), NIH/5T32CA119930-03 (DF) and NIH/1R21EB010196-01(DF), which are greatly appreciated. Finally, we thank Texas Advanced, Computing Center, the University of Texas at Austin for allocating computational time on their supercomputing facilities.

Declaration of interest: The authors report no conflicts of interest. The authors alone are responsible for the content and writing of the paper.