Temperature superposition for fast computation of 3D temperature distributions during optimization and planning of interstitial ultrasound hyperthermia treatments

Abstract

Purpose: A temperature superposition method has been developed for fast optimisation and planning of interstitial hyperthermia treatments with convectively cooled multi-transducer ultrasound applicators integrated within high dose rate (HDR) brachytherapy catheters.

Methods: Steady-state temperature distributions produced by individual tubular transducers capable of directional heating were pre-computed using finite element models (FEM) methods. The composite temperature distributions generated by multi-applicator implants were approximated as superposition sums of the pre-computed temperature profiles. Composite temperature distributions produced by the multi-applicator implants were also computed using accurate but computationally expensive FEM methods (considered here as the validation standard). Both methods were used for temperature calculation on a range of test implant geometries and representative patient cases (HDR implants in prostate (n = 13) and cervix (n = 2)), with optimised treatment plans created for the latter.

Results: Difference between temperatures calculated by the superposition and FEM methods was below 0.37°C (95% confidence interval) in test implants at clinically relevant acoustic intensities (0.3–2.0 W/cm²) and blood perfusion (2 kg/m³/s). Difference in 41°C isothermal volumes was below 8.3%. Superposition-based optimisations followed by FEM forward calculations (hybrid plans) were completed 4–7 times faster than FEM-only plans (FEM optimisation + FEM forward). Mean T₉₀, T₅₀ and T₁₀ values from both plans were within 0.3°C, 0.4°C and 0.45°C respectively, and the mean acoustic intensities were within 0.23 W/cm².

Conclusions: Temperature superposition provides a fast technique for forward or optimised planning of interstitial ultrasound hyperthermia treatments with calculations comparable to more accurate but time consuming FEM methods.

• hyperthermia
• fast optimisation
• fast treatment planning
• interstitial ultrasound
• temperature superposition

Introduction

A temperature superposition technique was devised for fast calculation of three-dimensional (3D) heating distribution patterns produced during interstitial ultrasound hyperthermia treatments. This computationally efficient method was applied for hyperthermia treatment planning with patient-specific optimisation in the study presented here.

For effective hyperthermia treatment, it is critical that sufficient minimum temperatures (T₉₀ or T_min > 40°C) and cumulative thermal dose (6–10 CEM43°C) be delivered, while ensuring that temperature levels associated with toxicity are not breached [1], [2]. Often, the ability to reach therapeutic temperature levels in the target may be limited by complications due to temperature hotspots caused by factors such as patient anatomy, tumour location and choice of heating modality [3]. Hence, hyperthermia treatment planning platforms are being increasingly used in the clinic for pre-treatment evaluation. These planning frameworks may utilise numerical modelling to simulate 3D temperature distributions. Finite element models (FEM) [4] or finite difference (FDTD) [5] methods have been employed to compute position dependent specific absorption rates (SAR), based on the type of treatment energy modality, and the concomitant temperature profiles. Following SAR computations, the temperature calculations may include relatively simple bio-heat transfer equation solutions assuming homogenous blood perfusion [6] or more involved approaches which account for physiological perfusion changes [7] or discrete vasculature models [8]. Patient-specific treatments can be generated in several planning platforms by obtaining the patient anatomy from segmented computed tomography (CT) [4], [6], [8], [9] or magnetic resonance (MR) [10] images. Such planning methods have been instrumental in improving treatment efficacy by reducing hotspots [3], [11] and improving target coverage in terms of T₉₀, T₅₀ and T₁₀ [8].

Some hyperthermia planning frameworks also include optimisation routines which seek to maximise the energy delivered to a target region while limiting heat exposure in the surrounding healthy anatomy. Typically, these are implemented using objective functions defined in terms of temperature [4–6], [12], [13], thermal dose or SAR [7], [14–17]. SAR-based optimisation can be implemented efficiently but these calculations do not take into account blood perfusion changes, applicator cooling and conduction effects. Studies have shown that hotspots predicted by SAR-based metrics do not always correspond to temperature hotspots [18]. Also, treatment bioeffects correspond to the delivered temperature or thermal dose rather than energy deposition [2], [19]. Temperature-based optimisation has been shown to result in better treatment plans than SAR-based methods [7].

High-resolution temperature based optimisation may require excessive computation times which may not be practical or feasible in clinical settings with limited planning time. To expedite the optimisation process, low resolution temperature [6] or SAR [20] models may be used to obtain optimal parameters, and a comprehensive treatment plan may be generated using high resolution steady-state or transient temperature models. Efficient objective functions that exploit eigenvalue and eigenvector normalisation can also be used to speed up the optimisation process [20]. Similarly for fast optimisation, information about the patient anatomy can be used to make experience-based guesses and select specific points to evaluate the objective functions [6], [19]. Temperature superposition for fast temperature calculations has been explored for external, multi-focus ultrasound phased arrays [21] and deep externally applied radio frequency (RF) sources [19], [22]. The energy modality considered in this study utilises catheter-cooled, directional, interstitial ultrasound applicators. Implementation of temperature superposition with these devices is more complicated because of inhomogeneous heating and high thermal gradients, and hence needs to be explored further.

The development, validation and implementation of superposition-based temperature computation method for fast planning and optimisation of multi-applicator interstitial ultrasound hyperthermia treatments are reported in this paper. In this study, the superposition-based calculations were validated with respect to more 3D FEM models (considered the standard herein) for device geometry and positioning representative of clinical hyperthermia implants at multiple input powers and blood perfusion values. Optimised treatment plans were obtained for a series of representative hyperthermia patient cases (in prostate and cervix) using both the superposition methods developed here and FEM models. Treatment plans generated from both frameworks were compared with respect to calculated power levels, temperature distributions (T₉₀, T₅₀, T₁₀), and computational efficiencies. These quantitative comparisons were used to establish the validity and applicability of a hybrid superposition/FEM approach as an alternative to the FEM-only approach in optimisation and planning of treatments within the limited time resources available in a clinical setting.

Methods

Catheter-based ultrasound devices

The fast temperature calculation methods devised in this study were applied to hyperthermia treatments delivered using catheter-based ultrasound applicators [23–26]. These devices consist of longitudinally sectored, independently powered, tubular transducer elements arranged as a linear array. They can be inserted within selected 13-gauge plastic catheters that have been surgically implanted to administer high dose rate (HDR) brachytherapy. When performing a heat treatment, these applicators are cooled by circulating water through the catheters in order to couple the ultrasound energy and increase thermal penetration. These interstitial devices can preferentially heat tumour volumes with 3D control in angle and length. Typically, such applicators employ tubular transducers which are 10 mm long, 1.5 mm outer diameter, 6.5–8.5 MHz natural frequency and active sectors of 180°, 270° and 360°.

Biothermal and acoustic models

During hyperthermia treatments, the target tissue is typically maintained at an elevated temperature for 60–70 min. To model this situation, temperature distributions obtained during interstitial ultrasound hyperthermia were approximated using the steady-state version of Pennes bioheat transfer model in Cartesian coordinates, similar to previous studies [6], [8]. This is represented in Equation 1 where energy balance between ultrasound absorbed by the tissue and the heat redistributed in the body through conduction and blood perfusion is described aswhere T is the tissue temperature, k is the thermal conductivity, ω_b is the blood perfusion, C_b is the specific heat of blood, T_b is the blood temperature, Q is the amount of incident ultrasound energy converted to heat, and the ∇ operator refers to partial derivative in space.

For multi-applicator interstitial ultrasound implants, the total heat deposition was proportional to the cumulative acoustic energy from all transducers absorbed by the tissue volume. This is described in Equation 2 aswhere n is the number of interstitial ultrasound applicators used in a treatment and m is the number of transducers per applicator. The heat generated by each transducer is given by Equation 3:where f₀ is the transducer frequency, α is the ultrasound absorption coefficient, µ is the ultrasound attenuation coefficient, η_i is the transducer efficiency, P_i is the electrical power input, r₀ is the transducer radius, and l_i is the transducer length [27]. The attenuation and absorption coefficients were adjusted to account for acoustic energy lost in the cooling catheters. For each transducer, a transformed coordinate system, denoted by suffix i, was used. To obtain such a system, the Z axis was set along the length of a transducer, the x axis was set along the transducer tube diameter bisecting the active sector angle θ_i, and the origin was set at the centre of the cylindrical transducer tube. r_i is the Euclidean distance from the Z axis after the coordinate transformation. Θ and H are rectangular window functions that are unity for |arctan⁻¹(y_i /x_i)| ≤ θ_i /2 and |z_i| ≤ l_i /2 respectively, and zero outside these ranges. They were included in order to model directional devices where the deposited ultrasound energy was assumed as bound in space by the active transducer sector angle and length. The coordinate transform has been illustrated in Figure 1.

Finite element methods

Three-dimensional temperature distributions were numerically computed using FEM methods implemented with Comsol 3.5 (Palo Alto, CA, USA). Pennes equation described in Equation 1 was evaluated using the PARDISO stationary solver provided in Comsol. A fine mesh resolution was used near the ultrasound applicators consistent with the dimensions of the cooling catheter (0.26 mm). Based on mesh convergence criteria for a stable thermal solution, the maximum allowable size for FEM mesh tetrahedral elements near the catheters was set to 1.5mm with a growth rate/ratio of 1.11. Throughout the simulation volume, the maximum allowable tetrahedra dimension was set to 5.0 mm. Typical full resolution FEM meshes consisted of 40,000–60,000 elements. These settings were also used by Chen et al. [6] and allowed stable computation of the temperature field, especially near the applicators. Dirichlet boundary condition for the target tissue was constant temperature (T_b) and convectively cooled for the catheter–tissue boundary.

Here, r_i is radial distance from the ith catheter/applicator axis, h is convective cooling coefficient, T_water is temperature of the cooling water and T_b is the nominal body/blood temperature. Table 1 lists the values with units for all constants used in these models [6]. FEM models were considered as standard and were used in optimal planning and also in the validation of fast approximate methods for temperature calculations, described next.

Table 1.  List of parameters used in bioacoustic temperature modelling.

Parameter	Units	Value
k (thermal conductivity)	W/m/°C	0.56
ωb (blood perfusion)	kg/m^3/s	2.0 (also 1.0 and 5.0 in test cases)
Cb (specific heat of blood)	J/kg/°C	3720
Tb (blood temperature)	°C	37
f0 (centre frequency)	MHz	7.0
α (absorption coefficient)	Np/m/MHz	5.3 (prostate), 6.9 (cervix)
μ (attenuation coefficient)	Np/m/MHz	5.3 (prostate), 6.9 (cervix)
Catheter α and μ	Np/m/MHz	40
r0 (transducer radius)	Mm	0.75
l (transducer length)	Mm	10
h (cooling coefficient)	W/m^2/°C	100

Temperature superposition technique

Calculation of temperature distribution at a spatial point by superposition is expressed in Equation 5. Temperature distribution (T_i) due to a single, sectored, catheter cooled ultrasound transducer (ith) with input power P_i (P_i = 0 when calculating cooling) was computed by numerically solving the bio-heat transfer problem outlined in Equations 1–4 with high resolution 3D FEM methods implemented in Comsol (similar to the description above). The calculated temperatures were normalised with respect to cooling, and the resulting temperature increase for the ith transducer as a function of input power is denoted by [P_i]. Temperature decrease due to cooling with respect to the basal temperature (T_b) is denoted by . Finally, the temperature at a given spatial point heated by a multi-applicator implant computed using the superposition method (T_super) is expressed as the sum of the cumulative temperature increase due to all powered transducers, the cumulative temperature decrease because of the cooling water flow, and the basal temperature.

Temperature superposition for a representative two-element ultrasound applicator is shown in Figure 2. To facilitate fast planning, temperature distributions generated by individual transducers at known power and perfusion values were stored in a look-up table. The relation between the acoustic power input and temperature rise is not a simple linear relationship at all spatial locations (Equation 1) due to the presence of applicator cooling and steeply radial divergent cooling below normothermic baseline. Thus, multiple data sets of temperature profiles for different acoustic power levels are implemented.

Figure 1. Three-dimensional coordinate transform performed to calculate the ultrasound energy deposited by the ith transducer is illustrated in the Z_i = 0 (A) and Y_i (or Θ_i) = 0 (B) planes. The origin of this transformed coordinate system was set at the centre of the transducer tube and the aiming direction was set along the positive X_i axis. The ultrasound energy was assumed as zero for |θ_i| > Θ/2, where Θ was the active sector angle for the transducer (A). The ultrasound energy was assumed as zero for |z_i| > H/2, where H was the height of the transducer (B).

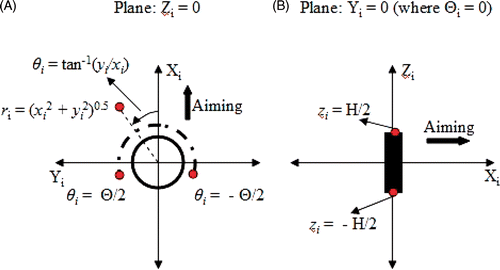
Figure 2. Example of temperature superposition shown with (A) temperature increase due to the first transducer powered at 4 W/cm² [T₁], (B) temperature increase due to the second transducer powered at 4 W/cm² [T₂], (C) approximate temperature increase modelled as the sum of temperature increases due to individual transducers [T_approx = T₁ + T₂].

Temperature profiles were generated for acoustic power values between 0–1 W (0–4 W/cm²) in steps 0.025 W (acoustic) on a non-uniform spatial grid. The spatial sampling was chosen to enable reliable thermal profile reconstruction coupled with efficient data retrieval from the look-up table. Details about the grid points can be seen in Table 2. Each temperature profile was computed at 6137 spatial locations, as specified in Table 2. Temperature profiles were computed for 40 distinct acoustic power values for each transducer sector type (180°, 270° or 360°), perfusion level (1, 2, or 5 kg/m³/s) and tissue type (prostate or cervix). The resulting look-up table had a total of 720 files where the temperature data was stored in ‘.mat’ format (Matlab 7.1, Mathworks, Natick, MA). The memory size of the complete look-up table was 32 MB.

Table 2.  Spatial grid in cylindrical coordinates for creating temperature look-up tables.

Coordinate	Range	Resolution
Radial (r)	1.2–10 mm	1 mm
	10–30 mm	5 mm
	30–60 mm	10 mm
Angle (θ)	−180°–180°	20°
Height (z)	−30–−10 mm	5 mm
	−10–10 mm	2 mm
	10–30 mm	5 mm

To recreate a 3D temperature map of a single transducer segment at a required power value, temperature values at the two closest available powers were retrieved from the look-up table. Temperatures at the intermediate spatial locations were estimated by performing a cubic spline-based interpolation. To obtain temperature values at the intermediate power level, a linear interpolation was performed between corresponding spatial points of the two recreated temperature profiles. To recreate a 3D temperature map of a multi-applicator and multi-transducer configuration, temperature values obtained through interpolation were substituted in Equation 5, following coordinate transformations described 0. Data retrieval from the look-up table, temperature interpolation and temperature superposition were implemented in Matlab 7.1.

Validation of superposition-based temperature models

Quantitative agreement between the superposition-based and FEM-based temperature calculations was investigated using several test configurations such as

• single four-element applicators,

• linear implants consisting of four, coplanar, parallel, four-element applicators spaced 8 mm apart and aimed orthogonal to the plane containing these devices,

• circular implants consisting of parallel, four-element applicators arranged in a hexagonal cluster (side length = 20 mm), all aimed at the central axis of the implant.

All applicators in an implant were assumed to be identical. Applicators with 180°, 270° or 360° transducer sectors were evaluated in these test configurations. Complete temperature distributions were simulated using the superposition technique and compared to FEM-based methods, with all transducers in an implant driven at the same power level. The nominal value for blood perfusion was set to 2 kg/m³/s. For some test cases, comparisons between the two simulation methods were also conducted for 1 kg/m³/s and 5 kg/m³/s perfusion.

Integration of temperature superposition technique within optimisation framework

Both FEM and the superposition methods were used in retrospective planning of interstitial hyperthermia treatments in prostate and cervix. A temperature-based optimisation scheme was used to maximise the target volume above 41°C [6] with constraints on maximum allowable temperature values in the bladder of 42.5°C, in the rectum of 41.5°C [28], in the urethra of 43.5°C, and 47°C [29] for the overall global maximum. This was reformulated as an unconstrained quasi-Newton optimisation to minimise:where

For the results presented in this paper, penalty parameter β was set to 10⁶ [6]. The high penalty weights ensured that C₁–C₄ remained zero in the optimised plans and the temperature safety limits were not breached. The initial acoustic intensity was set at 0.64 W/cm² for each transducer so that the starting solution was valid with zero valued C₁–C₄. The objective function was evaluated at uniformly spaced (2–3 mm) points in the target volume and the urethra, and all points on the bladder and rectum contours. This amounted to 2500–3000 spatial locations in each implant case.

The optimisation framework was utilised to furnish three different plans:

1. FEM-only plan (FEM optimisation + FEM forward model).

2. Hybrid plan (superposition optimisation + FEM forward model).

3. Superposition-only plan (superposition optimisation + superposition forward model).

The quality of heating achieved by the hybrid and superposition-only plans, and the computational resources they used were compared to the FEM-only plans, considered as the standard. All treatments were planned on a desktop computer with 3.8 GB RAM, 2.4 GHz dual core processor and Ubuntu 10.04 operating system.

Description of patient cases

Representative implant configurations from 15 HDR brachytherapy patients (13 in prostate and 2 in cervix) were used to evaluate the patient-specific fast planning for interstitial ultrasound hyperthermia treatments. For the patient cases considered here, bladder, rectum, urethra (where applicable), and the implanted catheters were manually segmented from computed tomography (CT) images acquired immediately before the brachytherapy procedure. These structures were identified and delineated by a physician using a commercial HDR treatment planning programme (Oncentra by Nucletron, Veenendaal, the Netherlands) [6]. For a particular case geometry, the applicator sector angles and aiming directions were chosen based on prior experience with these treatment procedures [1], [29]. The optimised treatment plans were evaluated using T₉₀, T₅₀, and T₁₀ metrics within the target volume.

Results

Validation of temperature superposition

Temperature distributions for representative implant configurations described in subsection 0 were calculated using the superposition-based and FEM-based methods where acoustic intensity of each transducer was chosen to achieve a maximum temperature between 47.0 ± 0.2°C in the treatment volume, consistent with the temperature constraints above.

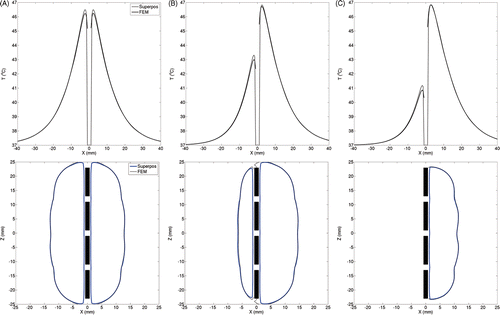
For a four-element ultrasound applicator (Figure 3, top row), radial temperature traces calculated using both methods show excellent agreement at distances of 8 mm or greater from the device. For 3.2 W/cm² acoustic intensity to each transducer, difference in the temperatures predicted by both methods was below 0.4°C (ω_b = 2 kg/m³/s). Deviations of such magnitudes in the temperature estimates occurred close to the applicator. Away from the applicators, the deviations were negligible. For sectored applicators, tissue volumes spanned by inactive regions of the transducer elements were heated primarily through conduction. In these regions, the temperature was overestimated by superposition as compared to FEM. This can be observed close to the device along the negative x-axis on the radial temperature traces. Critical isotherms at 41°C, often used to quantify target coverage during hyperthermia treatments, are shown in the bottom row of Figure 3. These have been plotted for a longitudinal section through the device and calculations made by both the superposition and FEM methods show excellent agreement.

Figure 3. To compare temperature distributions calculated for a single four-element applicator using the superposition-based and FEM-based methods, radial temperature profiles have been plotted through the device centre (top row) along with 41°C isotherms estimated in longitudinal planes through the devices (bottom row). The radial temperature plots shown in the top row represent essentially temperature values along the X-axis (positive X-axis is the aiming direction and Z = 0 is the applicator centre). Plots have been generated for devices with (A) 360°, (B) 270° and (C) 180° transducer sectors. The acoustic output of each transducer was set to 3.2 W/cm². For directional applicators, positive X-axis was set as the aiming direction. A constant blood perfusion of 2 kg/m³/s was assumed.

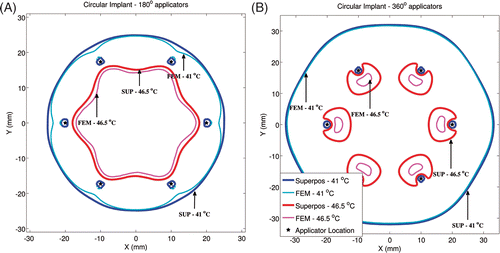
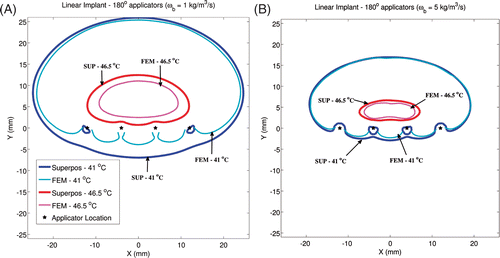
Critical isotherms at 41°C corresponding to target coverage and 46.5°C corresponding to hotspot locations for linear and circular implant geometries can be seen in Figure 4 and Figure 5 respectively (ω_b = 2 kg/m³/s). For linear implants with 180° sectors, similar to most clinical implants selected in this study, excellent agreement was seen in the shape of the 41°C isotherm calculated by the superposition and FEM-based methods in the direction of ultrasound propagation (positive Y-axis). Consistent with Figure 3, temperatures were over-predicted by the superposition method in regions where direct ultrasonic heating did not occur (‘behind’ the implant along the negative Y-axis). In implants with 360° transducers, similar agreement was observed for 41°C isotherms computed by both methods. For linear implants with 180° transducers, the maximum temperatures computed by both methods were within 0.7°C and the hotspot locations were within 4 mm. For linear implants with 360° transducers, the maximum temperatures computed by both methods were within 1.2°C and the hotspot locations were within 1 mm. The circular implants with 180° and 360° applicators showed better agreement between the shapes of the 41°C and 46.5°C isotherms calculated by both methods, as compared to the linear implants. For circular implants with 180° transducers, the maximum calculated temperatures differed by less than 0.5°C and the hotspot locations differed by less than 2.8 mm. For circular implants with 360° transducers, the maximum calculated temperatures differed by less than 0.9°C and the hotspot locations differed by less than 1 mm. For all test implant configurations, temperature values calculated using the superposition method were statistically greater than FEM-based calculations. However, at 95%CI, there was insufficient evidence to prove that the difference between the temperatures calculated by both methods was greater than 0.07°C (based on a paired one-tailed t-test).

Figure 4. Critical isotherms at 41°C and 46.5°C have been calculated using the superposition-based and FEM-based methods in a representative linear implant (similar to posterior peripheral implants from the clinical cases). Results have been plotted for (A) implant with 180° transducers aiming in the positive Y-axis and with each transducer powered to 1.54 W/cm², (B) implant with 360° transducers and with each transducer was powered to 1.1 W/cm². Acoustic powers were chosen such that a maximum temperature close to 47°C was obtained. A constant blood perfusion level of 2 kg/m³/s was assumed.

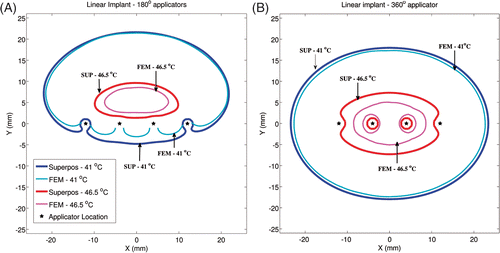
Figure 5. Critical isotherms at 41°C and 46.5°C have been calculated using the superposition- and FEM-based methods in a representative circular implant (similar to peripheral implants from the clinical cases). Results have been plotted for (A) implant with 180° transducers aimed towards the implant's central axis (Z-axis) and with each transducer powered to 1.92 W/cm², (B) implant with 360° transducers and with each transducer was powered to 1.46 W/cm². Acoustic powers were chosen such that a maximum temperature close to 47°C was obtained. A constant blood perfusion level of 2 kg/m³/s was assumed.

The impact of blood perfusion value on quantitative agreement between temperature simulations by FEM and superposition was investigated. To do so, blood perfusion values were set to 1 kg/m³/s and 5 kg/m³/s and temperature distributions were calculated for representative implants. Results have been plotted for an example linear implant in Figure 6 in form of 41°C and 46.5°C isotherms. The agreement between temperature contours obtained by both methods improves with increased perfusion values. Conversely, superposition-based temperature calculations opposite to the direction of ultrasound propagation show greater deviation from FEM calculations for low perfusion cases.

Figure 6. To investigate the impact of blood perfusion on the accuracy of superposition models, temperature distributions from a linear implant with 180° transducers have been plotted for two perfusion values. All transducers were powered to 1.2 W/cm² when perfusion was set to 1 kg/m³/s (A) and to 2.5 W/cm² when perfusion was set to 5 kg/m³/s (B). Critical isotherms at 41°C and 46.5°C have been plotted from temperature computations performed using the superposition and FEM-based methods. All transducers were aimed along the positive Y-axis. Acoustic powers were chosen such that a maximum temperature close to 47°C was obtained.

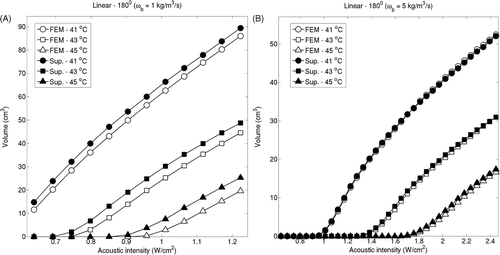
Isotherm volumes were also computed by varying the acoustic intensities from 0.3–1.8 W/m². For linear implants with 180° sectors (ω_b = 2 kg/m³/s), 41°C isotherm volume predicted by the superposition method differed less than 8.3% compared to the volume computed by the FEM-based models, as seen in Figure 7. For linear implants with 360° this difference was below 6.7%. For circular implants with 180° and 360° this difference was below 2.7% and 0.001% respectively. The difference in the two estimates showed a slight increase with respect to the acoustic input. The isotherm volume comparison was repeated for perfusion levels of 1 kg/m³/s and 5 kg/m³/s for representative implants and examples of linear implants with 180° sectors can be seen in Figure 8. Isotherm volumes computed by FEM and superposition were more closely matched for high perfusion cases, consistent with Figure 6.

Figure 7. Volumes of critical isotherms at 41°C, 43°C and 45°C have been computed for linear implants (top row) and circular implants (bottom row) with applicators consisting of 180° (A) and 360° (B) transducers driven at increasing acoustic intensities. Isotherm volumes were calculated using both the superposition-based and FEM-based methods. Blood perfusion was assumed to be 2 kg/m³/s for all cases. The highest acoustic intensity value in each panel corresponds to the intensity at which a maximum temperature close to 47°C was computed.

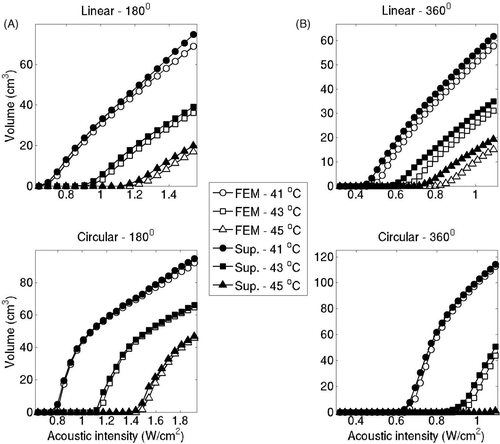
Figure 8. Iso-temperature contour volumes at 41°C, 43°C and 45°C for linear implant with 180° applicators were computed using the superposition-based and FEM-based methods for increasing acoustic intensities for blood perfusion levels of (A) 1 kg/m³/s and (B) 5 kg/m³/s. The highest acoustic intensity value in each panel corresponds to the intensity at which a maximum temperature close to 47°C was computed.

To further statistically quantify the agreement between temperature calculations by both the FEM and superposition methods, a simple linear regression was performed between the 41°C isotherm volumes computed by the FEM method and the input acoustic intensity values. For all test implants, the 41°C isotherm volumes calculated by the superposition method were within 95% confidence bounds of this fitted linear regression.

Evaluation of superposition based hyperthermia plans on representative patient implants

In three prostate and two cervix cases, a hyperthermia plan with three to six applicators embedded along the organ periphery was generated. Here, such an implant encompassing the perimeter of the target was called a peripheral implant, similar to the circular example implant geometry described previously. In 10 prostate cases, a hyperthermia target volume (HTV) was defined within the posterior section of the organ and a hyperthermia plan was generated to treat the HTV using three to five applicators embedded along the organ's posterior periphery. Such implants are similar to the linear implant arrangement described in the test cases earlier, and here they are called posterior peripheral implants. For the cases considered here, four-element ultrasound applicators were used for generating hyperthermia plans.

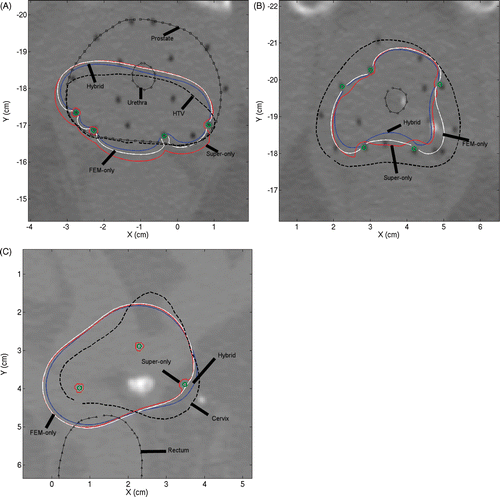
Axial slices through the mid-gland region are shown in Figure 9 for three representative patient cases. The first example is a posterior peripheral implant, comprising devices (shown in green circles) with 180° sectors, for treating an HTV (dashed line). The second example is a peripheral implant in the prostate consisting of devices with 180° sectors. In this case, no HTV was defined and the applicators were implanted along the entire prostate perimeter. The third example is a cervix case employing three 360° applicators, again in a peripheral configuration with no defined HTV. Based on the optimisation-inclusive planning, the transducer powers were tailored to maximise the target coverage while ensuring minimum toxicity to the surrounding healthy tissue. CT images from these cases have been overlaid with 41°C temperature contours obtained from the three optimal plans discussed earlier. The FEM-only plan (FEM optimisation + FEM forward model) is shown in white, the fast hybrid plan (superposition optimisation + FEM forward model) is shown in blue, and the superposition-only plan (superposition optimisation + superposition forward model) is shown in red. The target region could be heated effectively with both the hybrid and FEM-only plans. Consistent with the test cases presented in the previous subsection, the superposition-only plan based entirely on superposition models for both optimisation and forward calculations overestimated the temperature values.

Figure 9. Axial slice views of posterior peripheral (A) and peripheral (B) implants in prostate and peripheral implant (C) in cervix. The first two examples employed 180° applicators and the third 360° applicators. 41°C contours obtained by superposition/FEM hybrid plan (blue), FEM-only plan (white) and superposition-only plan (red) can be seen.

Comparison of plans calculated with the superposition-only, fast hybrid, and FEM-only (standard) was performed using T₉₀, T₅₀ and T₁₀ metrics for the target region (Figure 10). It should be noted that these implants were performed for HDR delivery and with no consideration for hyperthermia treatment efficacy and target volume coverage. These implants have been used here only to demonstrate and compare optimisations based on temperatures calculated by the superposition and FEM methods. In all cases, T₉₀ values of 40.3°C or greater were obtained by the hybrid plans, with average T₉₀ of 41.03°C. The average differences in T₉₀, T₅₀ and T₁₀ obtained for the fast hybrid plans and FEM-only plans (standard) were 0.31°, 0.4° and 0.45°C respectively. For superposition-only plans, average T₉₀ of 41.6°C was obtained due to the previously demonstrated temperature overestimation. The T₅₀ and T₁₀ estimates also followed similar trends with mean values of 42.7°C and 44.25°C for hybrid plans respectively. The optimal transducer intensities predicted by superposition and FEM methods are consistent with respect to their mean and standard deviation values, as seen in Figure 11. The hybrid and FEM-only plans employed acoustic intensities between 1–2 W/cm². Average difference between acoustic intensities estimated by both methods was below 0.23 W/cm².

Figure 10. Comparison of optimisation-based planning performance of superposition/FEM hybrid plan (white), FEM-only plan (grey) and superposition-only plan (black) in terms of T₉₀, T₅₀ and T₁₀ for all 15 implant cases. Cases 1–3 correspond to peripheral prostate implants, 4–13 are posterior peripheral prostate implants, and 14–15 are peripheral cervix implants. Blood perfusion of 2 kg/m³/s was assumed. FEM-only plan represents the standard to compare.

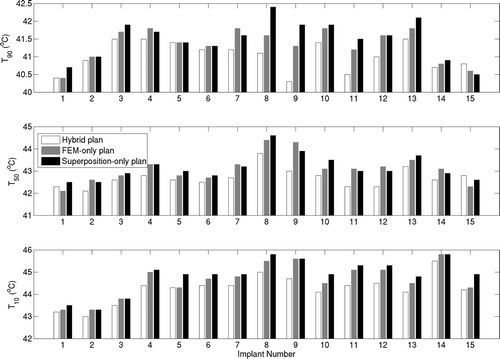
Figure 11. A comparison between transducer acoustic intensities obtained by the superposition- and FEM-based optimisation is shown for all 15 implant cases. Mean acoustic intensities obtained in example implants are shown and standard deviations are indicated by error bars.

The superposition and FEM-based optimisations yielded different sets of optimal solutions. Hence, the optimal power values used to generate the FEM-only and hybrid plans were different, leading to two different treatment plans. For the 15 implant cases considered here, the mean value for the paired difference between T₉₀s computed by both methods was 0.297°C and the corresponding standard deviation was 0.45°C. Hence, the two-sided 90%CI for this paired difference extended to 0.19°C on either side of the calculated mean value. This estimate is based on a large sample z-statistic computed using the calculated mean and standard deviation for the paired difference values. If the difference in means of T₉₀ values for equivalent FEM-only and hybrid plans is assumed to be 0.25°C, then the 90%CI extends between 0.06°C and 0.44°C. The observed mean difference value of 0.297°C for this study lies within this confidence interval indicating equivalence between the two plans (p-value = 0.023 in a paired two-sided t-test).

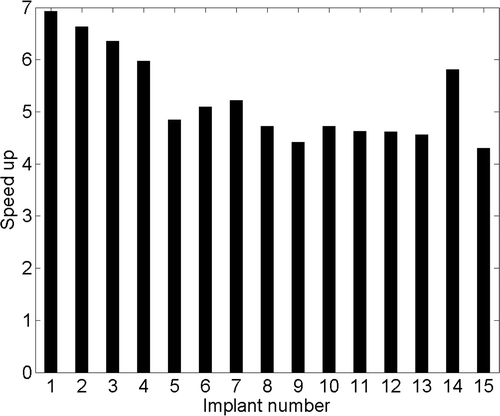
The computation time for a single iteration during optimisation increased with the number of transducer segments (number of variables) in both superposition and FEM-based approaches. For 8–20 transducer elements, time per iteration for FEM- and superposition-based optimisations was 3–19 s and 1–3 s respectively and the overall speed gain was 4.3–7. Typically, three to five ultrasound applicators consisting of four transducer segments are utilised during clinical implants giving 12–20 variables for the optimisation problem. For typical optimisation cases, temperature estimation during a single iteration took 8–12 s with the FEM model, and 1.5–2.5 s with the superposition model respectively. Consequently, optimisation based on the FEM model required in excess of 2 h to complete, while the superposition technique required approximately 30 min. For all implant cases chosen here, fast plans were completed in 10–35 min. A typical speed gain of 4.5–5.5 was observed between hybrid plans and FEM-only plans for the implant cases considered here, as seen in Figure 12.

Figure 12. Optimisation speed-up was defined as the ratio of time required per iteration during FEM-based optimisation and time required per iteration during superposition-based iteration. The speed gain obtained during optimisation has been plotted for all 15 patient implants.

Discussion

Temperature-based optimisation approaches and accurate 3D planning are important for a priori determination of implant strategy and initial applied power levels for multi-source interstitial ultrasound to best deliver therapeutic temperatures [6]. Computationally expensive FEM or FDTD methods can be used in such a scenario, but they can be impractical to implement in clinical settings with limited planning time. Fast superposition-based temperature calculations were developed in this study and applied for fast and accurate optimised planning of clinical interstitial ultrasound hyperthermia treatments.

In the past, McGough et al. [21] approximated the temperature rise induced by a multi-focus ultrasound phased array as the superposition sum of temperature increases due to the energy deposited at individual foci. They employed a fast analytic Green's function method to compute temperature distributions by assuming a focal spot as a point source of energy. Das et al. [19] pre-computed temperature distributions from external RF hyperthermia applicators and used superposition for fast temperature calculations. While optimising treatments they achieved significant improvement in computation efficiency by grouping regions in the target volume based on the temperatures that they may potentially reach and then performing optimisation on these grouped elements instead of individual points. Cheng et al. [22] used a Green's function approach to approximate the relationship between input power and temperature for external RF sources. They pre-calculated temperature profiles from known source configurations and used these as ‘virtual sources’ for optimising power levels of case-specific source positions. Inhomogeneous temperature distributions are produced by the catheter-cooled directional ultrasound applicators considered here to deliver interstitial hyperthermia treatments. The heating patterns produced by such unfocused ultrasound transducers are not amenable for point-source approximations similar to McGough et al. [21]. They also make temperature-based grouping of points in the target volumes as implemented by Das et al. [19]. The catheter cooling also complicates the application of a Green's function approach similar to Cheng et al. [22]. Due to the significant differences between interstitial ultrasound and the other heating modalities where temperature superposition has been already applied, a detailed numerical validation of the temperature superposition framework developed here has been carried out using representative test implant geometries and patient cases.

As seen in Figure 4–8, reasonably accurate calculation of 41°C isotherm shapes and volumes was possible by the superposition method for clinically relevant acoustic intensities and blood perfusion levels. Hence, the target coverage obtained in superposition optimised (hybrid) plans was comparable to the more complex FEM-based optimised plans (Figure 10). The average value of optimum acoustic intensities estimated by both methods were within 0.23 W/cm² (Figure 11), however a direct one-to-one correspondence between FEM- and superposition-based transducer input estimates was not always observed due to the inherently noisy multivariate objective function (with multiple local minima). When planning is done with FEM methods, the entire temperature distribution needs to be calculated during each optimisation step. The superposition method, due the look-up table of pre-computed temperature distributions, requires temperature computation only in locations where the optimisation objective function has to be evaluated. This leads to substantial time savings (Figure 12) and optimisation can be completed within 35 min, making the superposition method appropriate for situations with limited planning time. Such time constraints are encountered when patient imaging is immediately followed by HDR brachytherapy, and hyperthermia is administered immediately after the radiation fraction to ensure treatment efficacy [1]. This allows an automatic selection of a large number of spatial points from the contoured patient anatomy for evaluating the objective function (2500–3000 points selected for the cases considered here). Hence expertise-based and potentially time consuming selection of objective function evaluation points similar to Chen et al. [6] (50 spatial points) is not required to meet time constraints. Such automatic selection of evaluation points reduces the involvement required from an expert physician or technician in setting up treatment plans and makes this platform more amenable for further automation. As superposition methods furnish the hybrid plans in approximately 30 min, optimisations can be performed for multiple implant and device configurations during a single clinical treatment to select a combination that best meets the therapeutic need.

Some differences between the superposition-based and FEM-based temperature calculations may be attributed to differences in the modelling of applicator cooling. During superposition calculations, a single transducer section 10 mm long is assumed cooled by a 12 mm long cooling catheter section (1 mm on either end) to account for the inter-transducer spacing in heating applicators. In FEM calculations, individual transducer sections are assumed along a contiguous cooled catheter. This simplified method of modelling cooling during superposition has some effect on temperature estimation, especially closer to the applicator. For single applicator implants shown in Figure 3, these errors are small (<0.4°C). For implants with multiple applicators, the effect of cooling is more pronounced, leading to greater differences in the temperature calculations by both methods (Figure 4–6). Compared to FEM, the superposition-based methods slightly overestimate temperature levels, especially in regions spanned by inactive sectors of directional applicators that are heated only by conduction. This makes the superposition method sensitive to blood perfusion values (Figure 6). For high blood perfusion, temperature increase is pronounced in regions where the ultrasound energy is directly absorbed. Temperature rises due to conduction are mitigated by increased heat dissipation from the additional perfusion. Hence, agreement between the 41°C isotherm shapes estimated by FEM and the superposition methods improves with perfusion. There is some over-prediction at the centre of the implants (within the target volume) as seen for the 46.5°C isotherms in Figure 4 and Figure 5. This is attributed to high temperature gradients and thermal conduction which are neglected by superposition. However, simulation studies indicated that at therapeutic acoustic intensities, the locations and values of temperature hotspots differed negligibly for both superposition- and FEM-based calculations.

In the patient implants considered here, temperature over-prediction by the superposition method led to the overestimation of temperature at the rectum periphery. Superposition-based optimisation plans were initially generated with the rectum temperature constraint of 41.5°C. When the optimal acoustic intensities so obtained were utilised with FEM-based forward models, the resulting hybrid plans would estimate rectal temperatures significantly below the set constraint level. A slight manual increase in the acoustic intensities would also yield valid plans with better target coverage. To counter this suboptimal estimation of acoustic intensities due to the temperature over-prediction in superposition calculations, temperature constraint on the rectum (variable C₃ in Equation 4) was increased by 1°C (to 42.5°C) while conducting the superposition-based optimisation. This changed constraint value was obtained empirically through simulation studies done on representative test and patient implants. It should be noted that that in spite of this adjustment in the rectum temperature constraint, final calculated maximum temperature in the rectum for hybrid plans did not exceed 41.5°C. Similarly, all other temperature constraints in Equation 4 were also met. Future versions of this platform can include temperature constraint adjustments specific to patient anatomy and implant geometry.

The patient-specific treatment plans presented herein were for comparison of temperature and power metrics predicted by superposition and FEM techniques, and are not intended to investigate general performance of interstitial ultrasound. These example cases were retrospectively planned for typical implants performed for HDR treatment only, and positioning of catheters was not optimised to include hyperthermia delivery requirements [30], such as positioning applicators at the periphery of the target region with the energy directed inward. In this work the water-cooled catheters were implanted inside the target organ at 3–5 mm from the organ periphery (Figure 9), so in these cases tissue volume within the perimeter of the applicator implant was included while determining the target coverage metrics. For the implant example shown in Figure 9(C), the target organ was 1.5 cm longer than the four-element applicators included in this study. Hence, while evaluating T₉₀, T₅₀, and T₁₀ metrics, only the tissue volume spanned by the implanted applicator length was considered.

In its current form the temperature superposition method is limited to temperature calculations for material with spatially homogeneous thermal and acoustic properties, and constant blood perfusion levels. Any non-linearity, for example due to applicator cooling, should be known a priori. For the clinical situations considered here, where hyperthermia immediately follows the HDR fraction, it is very difficult to measure patient-specific and spatially dependent tissue properties and blood perfusion. The simplifying assumptions made here during temperature modelling are consistent with the available clinical information and practical considerations. The increase in planning in speed may allow optimisations to be performed at multiple sets of tissue properties and blood perfusion values. However, single-transducer temperature distributions have to be pre-computed for these different sets of parameters.

In future implementations, the fast superposition-based methods can be combined with applicator placement strategies suggested in Wootton et al. prior to catheter implantation surgery. In order to reach steady-state temperatures within the first 10–15 min of a treatment, starting powers may be scaled to achieve a quick ramp-up to the desired steady-state temperatures. For instance, Wootton et al. scaled starting power values by 30% over the first 10–15 mins of a treatment, followed by 60 min at the optimised power values [30]. Future developments to this framework may also utilise graphics processing units (GPU) and distributed computing platforms to further expedite thermal modelling and optimisation. Several recent publications have successfully demonstrated the implementation of FEM-based solvers GPU architecture [31–34]. Taylor et al. have reported a speedup of 10–14 times when implementing a 3D model with 45,000 tetrahedral elements on GPU instead of a central processing unit (CPU) [34]. A similar speed-up factor would lead to shorter computation times than the current implementation of the proposed superposition-based method. It should be noted that the temperature superposition technique may also be amenable to speed-up via parallelised computing, thereby reducing computation times even further. For instance, looking up temperature distributions at different power levels could be done in parallel by several cores of a GPU (or alternatively, nodes of a computing cluster), rather than the sequential look-up performed in this initial implementation.

Conclusion

A fast temperature calculation method has been devised using superposition approximation. Accurate 3D temperature distributions can be computed using this method four to seven times faster than full resolution FEM models. This method has resulted in a substantial reduction in computational complexity and time expenditure during interstitial ultrasound hyperthermia treatment planning. When this approach was integrated within an optimisation framework, the superposition-based methods yielded hyperthermia treatment plans which were quantitatively comparable to more complex FEM models with substantially reduced treatment planning time. Hence, these superposition methods can make patient-specific temperature-based optimisation of interstitial ultrasound hyperthermia practical and feasible for clinical application.

Acknowledgements

We would like to thank Vivian Weinberg, Principal Statistician, S/M cancer Center, University of California, San Francisco for her advice and suggestion regarding the statistical analysis employed during superposition and FEM model comparison.

Declaration of interest: This study was supported by R01CA122276, R44CA134169 and R01CA111981 grants from the National Institutes of Health (NIH). The authors alone are responsible for the content and writing of the paper.