A pilot study for clinical feasibility of the near-harmonic 2D referenceless PRFS thermometry in liver under free breathing using MR-guided LITT ablation data

Abstract

Objectives: The conventional implementations of proton resonance frequency shift (PRFS) magnetic resonance thermometry (MRT) require the subtraction of single or multiple temporal references, a motion sensitive critical feature. A pilot study was conducted here to investigate the clinical feasibility of near-harmonic two-dimensional (2D) referenceless PRFS MRT, using patient data from MR-guided laser ablation of liver malignancies.

Methods: PRFS MRT with respiratory-triggered multi-slice gradient-recalled (GRE) acquisition was performed under free breathing in six patients. The precision of the novel referenceless MRT was compared with the reference phase subtraction. Coupling the referenceless MRT with a model-based, real-time compatible regularisation algorithm was also investigated.

Results: The precision of MRT was improved by a factor of 3.3 when using the referenceless method as compared to the reference phase subtraction. The approach combining referenceless PRFS MRT and model-based regularisation yielded an estimated precision of 0.7° to 2.1°C, resulting in millimetre-range agreement between the calculated thermal dose and the 24 h post-treatment unperfused regions in liver.

Conclusions: The application of the near-harmonic 2D referenceless MRT method was feasible in a clinical scenario of MR-guided laser-induced thermal therapy (LITT) ablation in liver and permitted accurate prediction of the thermal lesion under free breathing in conscious patients, obviating the need for a controlled breathing under general anaesthesia.

• referenceless
• thermometry
• proton resonance frequency shift
• intervention
• motion robust

Introduction

Minimally invasive thermal therapy is a rapidly developing approach for the local treatment of cancer. The goal of local thermal therapies is to heat diseased tissue to induce coagulative necrosis or apoptosis. At the same time, the surrounding healthy tissue has to be maintained below thermal damage levels. In an optimal scenario, the spatio-temporal delivery of heat energy requires intra-operative control.

There are established guidelines of application for thermal therapies when they are demonstrated to be advantageous as compared to surgery, chemotherapy, radiotherapy and immunotherapy [1–5]. Overall, thermal ablations demonstrated minimal side effects, hence a significant reduction in associated morbidity and mortality. Outpatient procedures can be performed, including multiple lesions per session, and a wide spectrum of patients are eligible among those who are not surgical candidates. Another essential advantage of thermal ablation is that the treated area has no ‘thermal memory’, which enables repeated thermal ablation in the same region. The results of thermal ablation can be assessed in the short term, whereas chemo- and radio-therapies require longer periods of time to shrink the tumours.

Image-guided tumour ablation has been defined in distinct steps, namely planning, targeting, monitoring, controlling and follow-up. Magnetic resonance (MR) imaging provides fundamental advantages at each of these steps. Moreover, MR imaging at high field is the only modality that offers the potential to map temperature and energy deposition of tissue during the ablation procedure, thus enabling the operator to monitor the progress and the end-point of energy deposition. The preferred temperature-sensitive MR parameter is the proton resonance frequency shift (PRFS). MR temperature mapping based on the PRFS effect uses the complex signal acquired from the gradient-recalled (GRE) sequences [6] and has become an accepted technique to monitor thermal ablation therapies [3], [7–12]. The method offers two fundamental advantages: tissue-independence [13] (with the exception of adipose tissue), and a linear calibration from 0°C to 100°C [14]. The relative temperature can be calculated by scaling the difference between one phase image acquired before heating (also called the reference phase) and one phase image acquired time delayed (during the intervention) that contains the information regarding the temperature elevation.

The conventional implementation of PRFS-based MR thermometry (MRT) requires a repeated scan through the volume of interest, with the same organ and slice position, and with the same organ deformation, if any. These two time-point measurements, which are necessary for the phase subtraction, may be separated by a time span of the order of even 10 to 30 min. Despite the use of a breathing belt [15–17], pencil-beam navigators [18] or other encoding and triggering methods for the respiratory motion, the voxels in the acquired slice are always, to a certain degree, shifted between the acquisition of the reference phase and the later acquisition during the thermal treatment. After intervention swelling or shrinking of the heated tissue or adjacent tissues can also be expected.

Several approaches have been published that aim to reduce or eliminate these errors; Vigen et al. [15] and Senneville et al. [18], [19] discussed a multi-baseline (or equivalently, multi-reference) method. The multi-baseline thermometry acquires multiple reference phase images for different positions of the moving organ (e.g. preparatory mapping of the motion as a data set atlas), and generates the per-operatory temperature maps by choosing the images with the best correlation to be used for the phase subtraction. Rieke et al. [20] were the first to introduce a referenceless PRFS MRT method using spatial information (instead of temporal information) to isolate the temperature-induced PRFS phase shift. The principle of referenceless MRT is to split a single time-point phase map into: (1) the spatial reference (also called the background phase), and (2) the temperature-induced PRFS phase contrast [20]. The calculated background phase (instead of the temporal reference) is to be subtracted from the actual phase map intra-operatory, i.e. single time-point acquisition.

Referenceless MRT is intrinsically insensitive to inter-scan tissue motion, including intra-operatory induced swelling or shrinking. This is also insensitive to the magnetic field perturbation by an external object. Furthermore, referenceless MRT permits greater flexibility during the ablation procedure compared to temporally referenced MRT. For instance, the sequence parameters, as well as the slice position and orientation, can be varied during the intervention unconstrained by some a priori mapped space of events, and any susceptible artefact-free needle may be repositioned or additional applicators may be placed.

Although multi-baseline MRT was demonstrated to reduce inter-scan motion artefacts, its accuracy on abdominal organs under free breathing is limited by non-periodic or unique event motion, as for example the liver, which is moved and deformed by respiration, heart beat and peristalsis of the bowel and undergoes a slow drift [21]. Multi-baseline acquisition cannot compensate accidental motion as the required information has not been mapped before the event occurred.

The referenceless method originally described by Rieke et al. [20] was based on numerical interpolation using an empirical polynomial model (with L₂ metrics; typically up to the order of 6) to estimate the background phase from a rectangular, closed, thick border towards the inner ROI (Region Of Interest). Their approach opened a new perspective for PRFS-based MRT, nevertheless, their mathematical algorithm may lead to numerical difficulties, such as an ill-conditioned, large-size matrix to be inversed for finding the polynomial coefficients. A variant of the polynomial referenceless MRT was described by Grissom et al. [22] using reweighted l₁ regression to adjust the fit coefficients. This variant does not require a border set of unheated voxels, but the method may fail for larger heating areas.

The difficulty in referenceless MRT is the need to provide an unheated and artefact-free border for the ROI, which is used to reconstruct the background phase. The accuracy of the referenceless calculation of the temperature depends equally on the quality of the chosen border and on the quality of the reconstruction algorithm used for recovering the background phase. Overall, the thinner and the more flexible the border can be, the better the suitability for clinical intervention scenario.

Our referenceless MRT method, described and clinically evaluated in this paper, tries to improve the flexibility, accuracy and mathematical robustness of the temperature calculation in a clinical scenario. Our method is based on fundamental properties of the static magnetic field inside the matter, and on the theoretical frame of harmonic functions as described in reference [23]. The segments of the border that are to be used must satisfy the same conditions as stated in the original work of Rieke et al. [20], i.e. unheated, free of susceptibility artefacts and free of phase singularities. A comparison between reference phase subtraction (respiratory triggered) and referenceless temperature monitoring is presented here, using clinical data from six free-breathing patients treated with laser-induced thermal therapy (LITT) for liver malignancies under conscious sedation. Coupling this referenceless MRT method with the model-based, real-time compatible regularisation algorithm described in Kickhefel et al. [24] was also investigated, as an advanced approach, expected to (1) improve the precision of MR temperature maps below the ‘white noise’ intrinsic standard deviation, and (2) smooth out the residual irregularities of respiratory triggering, which act as additional ‘noise’ on pixel-wise temporal curves due to positional fluctuations of the true mass-point of tissue around the observed pixel of the image [25].

Materials and methods

Principles of near-harmonic referenceless PRFS MRT

The principles of our method for calculating the background phase of a GRE image are summarised here, according to Salomir et al. [23]. This background phase should be calculated and subtracted from the measured phase map during the intervention in order to isolate the temperature elevation. The essential mathematical details are recalled in the Appendix.

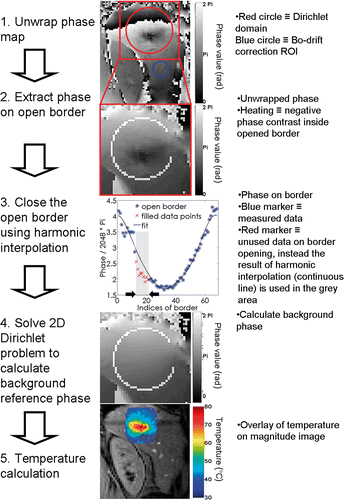
Taking a 3D domain with no sources of magnetic susceptibility (or with linearly varying susceptibility), the unwrapped phase of the GRE 3D data is demonstrated to be a harmonic function, which results in a null scalar field when the Laplacian operator is applied (see Appendix). Magnetic susceptibility inhomogeneities, localised heating or cooling of tissue, mixed signals from different chemical shift species with spatially varying ratios, or other artefacts, are all non-harmonic functions which contribute to the globally measured GRE phase [26]. Calculating the background phase thus means calculating the harmonic part of the phase map. The non-harmonic part of the GRE phase, in a homogeneous medium, constitutes the temperature elevation. Phase information along a one pixel thick border is theoretically sufficient to calculate the full harmonic background phase inside the domain (i.e. inner Dirichlet problem). This border has to be unheated and free from artefacts and susceptibility contrast. To enable slice-per-slice monitoring of temperature, the calculation of the background phase was reduced from 3D to 2D with a residual constant term in the phase's Laplacian. The solution of the constant Laplacian approximation in 2D is called here a near-harmonic function. To determine the residual term of the Laplacian operator, the border has to be at least two pixels thick. For practical reasons (mainly noise-robustness) we implemented a border three pixels thick. Moreover, openings in the border were compatible with the method by considering a circular geometry of the domain. The open border implementation permits the selective elimination of conflicting sectors from the assigned border. Conflicts may appear as deployment of heating, signal void pixels, flow artefacts, localised source of bulk susceptibility, or sharp susceptibility interfaces. If such erroneous conditions are ignored while writing the experimental border conditions of the Dirichlet's problem for the background phase, local or global errors would occur in the calculated temperature maps.

Firstly, the open border was re-filled to a closed border using harmonic interpolation (similar to partial Fourier techniques, see details in Salomir et al. [23]), which intrinsically excluded temperature-induced non-harmonic phase shift contributions over the repaired segments. Secondly, the information of the virtually closed border was used to solve the inner 2D Dirichlet problem, generating the background phase as output. Thirdly, the background phase was subtracted from the acquired phase map. The main steps involved in calculating the referenceless temperature are illustrated in Figure 1. Note, any GRE phase shift due to susceptibility changing outside the Dirichlet's domain (including changes from outside the imaging plane), is automatically corrected with the proposed 2D referenceless method.

Figure 1. Steps of numerical calculation of the referenceless temperature map. The inner border of the Dirichlet's domain is shown. To determine on-the-fly the average curvature of the 2D phase map, a double border is required (3-pixel total width).

Phantom studies

Prior to hepatic laser ablation patient protocol, preliminary phantom studies were conducted by using MR-guided focused ultrasound (MRgHIFU) heating in moving ex vivo tissue, as described in the Appendix, to investigate some fundamental properties of the proposed algorithm and to demonstrate its intrinsic stability and precision. Scanner built-in adaptive combination of the multiple coil signals and reconstruction (mGRAPPA) of parallel acquisition data were demonstrated in phantoms to not yield phase information distortion that might break the near-harmonic condition in the 2D GRE phase map.

No external sensor for cross-validation of temperature measurement was used in phantoms (e.g. thermocouple or fluoroptic fibre) because such a device could disturb the local magnetic susceptibility, may contaminate with air bubbles the tissue around the tip during insertion and acts as a strong reflector for the HIFU beam, thus inducing strong alterations in the thermal pattern.

Clinical protocol for MR-guided laser ablation in the liver

Thermal ablations of liver malignancies were performed on a 1.5T MR clinical scanner (Avanto, Siemens HealthCare, Erlangen, Germany) using LITT in six patients. The study protocol was approved by the local ethics committee and written informed consent was acquired from all patients. Prior to the intervention, patients received local anaesthesia (20 mL of 1% prilocaine subcutaneously) and a mild anxiolytic intravenously (Haloperidol: 10 mg haloperidol, 100 mg pethinide; TEVA Generics, Radebeul, Germany). All procedures were performed by the same experienced interventional radiologist. A neodymium-doped yttrium aluminium garnet (Nd:YAG) laser (Medilas Fibertom 5100, Dornier, Wessling, Germany) was used, operating at a wavelength of 1064 nm and a maximum power of 100 W, which can irradiate with up to three applicators simultaneously. For each laser applicator, a micro-catheter system, with an outer diameter of 1.8 mm (RoweCath®, RoweMed, Parchim, Germany), was placed under MR guidance. The LITT approach was chosen for tumour ablation as the applicators are practically free of any susceptibility artefact and therefore are compliant with the homogeneous susceptibility hypothesis explained in the Appendix.

This microcatheter system consisted of a titanium needle with a tip of 1.5 mm in diameter and a surrounding transparent heat-resistant Teflon catheter with an outer diameter of 1.8 mm. After insertion, the titanium needle was replaced by a laser fibre (diffusive tip length = 30 mm) and thermal therapy was initiated. Depending on lesion size and location, two or three laser applicators were positioned as decided intra-operatively by the interventionist. When a single applicator was used, it was positioned in the middle of the tumour, piercing the two opposite margins. When multiple applicators were used, overlapping (at least 5 mm was mandatory) ellipsoid impact zones with the length of the active tip and a maximum width of 2.5 cm were estimated. The MR-guided needle placement was performed interleaved using a FLASH (fast low angle shot) (TE 4.8 ms (echo time), TR 100 ms (repetition time), BW 260 Hz/pixel (bandwidth)) sequence with the patient bed shifted out of the magnet. How often the patient bed was shifted out of the magnet depended strongly on the position of the tumour and its reachability; an average of four cycles was necessary. One applicator was placed in about 15 min. The energy of the laser was applied continuously over 20 min, with gradually increasing power from 8 to 14 W in the first 3 min (increments of 2 W/min) and the flat-top energy of 14 W was maintained for the last 17 min. The ablation protocols were decided independently from the use of MRT monitoring and were not adjusted online. The energy delivered effectively was recorded by the device as listed in Table I.

Table I.  Overview of clinical data for the patients included in the study. A typical duration of fibre placement was 20 min per fibre and the effective ablation for each patient was about 20 min.

Patient	Tumour size (cm) transversal	Tumour size (cm) saggital	Liver segment	Number of applicators	Laser energy (kJ)	Tumour histology	Age/sex
1	3.8 × 3.3	3.5 × 2.7	8	3	48.1	GC	67/male
2	2.2 × 2.1	2.5 × 2.2	4	2	32	RC	62/male
3	5.0 × 2.7	4.9 × 3.3	8	3	37	GC	67/male
4	2.0 × 1.9	2.2 × 2.1	8	2	32.7	CM	68/female
5	5.0 × 3.8	4.8 × 3.1	2	3	44	RC	62/male
6	5.2 × 4.8	4.8 × 3.7	4	2	27.5	BC	58/female

GC, gastric adenocarcinoma; RC, rectal carcinoma; CM, colorectal metastases; BC, breast carcinoma.

Online temperature monitoring simultaneous to the procedure was implemented with a FLASH GRE sequence. The FLASH GRE sequence (TA 950 ms (acquisition time), TR 22 ms, TE 12 ms, FA 35°, BW, 250 Hz/Px; voxel size 2.5 × 2.5 × 6 mm³; spectral selective saturation of lipid signal, FOV 320 × 320 mm², matrix size 128 × 128, parallel acquisition GRAPPA 3, spine coil and body array coil combined 15 elements) was triggered using the scanner's built-in breathing sensor belt. In each breathing cycle, one sagittal and three transversal slices were acquired sequentially, yielding acquisition time per measurement of 3.8 s. From preliminary tests with the current FLASH GRE sequence, this value of the acquisition time was found on average to be the best compromise between intra-scan residual motion artefacts and image SNR. The effective temporal resolution depended directly on the breathing cycle intervals of the patient.

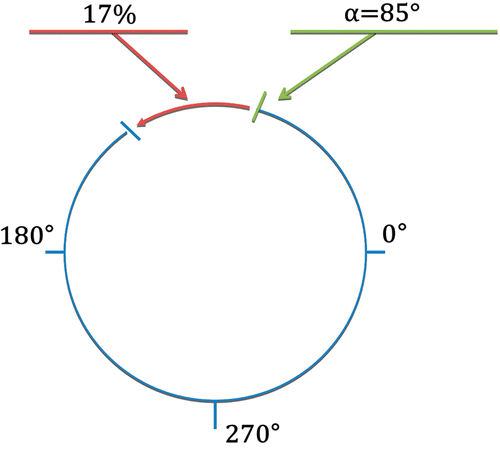
During the entire intervention, online temperature monitoring was used as a safety tool, to ensure that no at-risk organs or vessels were exposed to the laser heating. While the ablation protocols were pre-defined and not adjusted online, the physician was able to interrupt the treatment if such thermal risk was identified. The temperature elevation was monitored online for each treatment, and displayed on the main screen of the MR work station, as a colour overlay to the corresponding magnitude image. The underlying method of automatic temperature calculation behind the online display was the slice-per-slice reference phase subtraction (monitored with the FLASH GRE sequence), whereas referenceless method (under validation throughout the study) was applied as post-processing. For the reference phase subtraction thermometry, the radiologist had to acquire a multi-slice reference image before heating. To enable offline realistic testing of referenceless thermometry, the radiologist positioned intra-operatory (i.e. in situ) the slice-specific ROI for the background reference phase calculation (i.e. Dirichlet's domain including the heated anatomical region), and could define one open segment in the border to exclude potential artefacts. The radius of this ROI for the referenceless MRT calculation ranged between 10 and 17 voxels (6 to 9 cm ROI diameter, given the in-plane resolution). Note that in both scenarios, user interaction was only required at the beginning of the intervention to position the monitoring ROI (reference phase subtraction) or to define the border for the background phase calculation domain (referenceless method) upon the total number of active applicators and the anatomic position of the tumour. To control the positioning of the open sector on the border (as required for referenceless background reconstruction), the border was visualised within the online display. In this study, a single open border segment was defined for each slice, aiming to avoid border phase conflicts such as tissue heating, flow artefacts originating from vena cava, or susceptibility discontinuities whenever target tissue was near the liver capsule. Size and angular position of the open segment were defined by two parameters, see Figure 2, with a maximum size restricted to a quarter of a circle. The first parameter was the angular origin of the segment along the circle, while the second parameter defined the ratio between the size of the open border sector and the total perimeter of the circle (expressed as a percentage). An initial configuration was maintained through the full data set of one ablative procedure.

Figure 2. Open border with one open segment defined using two parameters: a starting angle α, and the ratio of the segment length to the circle perimeter. For a given calculation, the same parameters were used both for the inner and outer border of Dirichlet's domain.

The follow-up examination (24 h after intervention) included bolus contrast-enhanced (0.2 mL/kgBW i.v. Gadovist, Bayer-Schering, Berlin, Germany) MR-images (FLASH 2D sequence with a TR 115 ms, TE 5 ms, TA 1 s, 30 slices, flip angle 70°, no fat suppression, same voxel size as for the thermometry sequences, 30 transversal slices). Unperfused tissue was defined as non-enhanced (hypo-intense) regions after the administration of the contrast agent.

Retrospective evaluation of data after intervention

The raw data from the thermometry acquisition for each patient was extracted from the host computer of the scanner and post-processed offline on an external PC, using the same image calculation environment (ICE, Siemens Healthcare, Erlangen, Germany) that was running in real time on the MR image reconstruction CPU. Computing time for referenceless MRT was less than 100 ms/slice, increasing with the size of the Dirichlet domain as N³.

Offline comparison was performed between the reference phase subtraction method and the novel referenceless method. The two methods were applied to identical raw data sets on a slice-per-slice basis. The measured temperature elevation was considered in unheated regions of the liver (i.e. baseline assessment, or ‘zero’ measurement stability) and, respectively, in the LITT-heated region.

The unheated ROI was a circle of radius 3 pixels positioned inside the Dirichlet domain but sufficiently far from the laser applicator(s) as to evaluate the precision of each MRT method (reference phase subtraction and near-harmonic referenceless). The spatio-temporal stability (or precision) of the MRT baseline was calculated using a three-step process. Firstly, a temporal standard deviation of temperature (t-SDT) was determined on a pixel-by-pixel basis from the series of dynamic measurements during an early stage of the procedure (e.g. 30 measurements). That is, a map of pixel-by-pixel t-SDT was established inside that unheated ROI. Secondly, a mean value of the t-SDT over all pixels from inside the unheated ROI was calculated. For the reference phase subtraction method, a B_o-correction must be performed to correct for the phase drift [27]. This phase drift was removed on slice-per-slice basis before computing the t-SDT using the information from one additional small ROI positioned outside the Dirichlet domain, see Figure 1. For the referenceless method, no B_o-correction was necessary, as any B_o-drift components are automatically removed in the calculation process. Third, an average over the interleaved slices was calculated as one global metrics of stability.

The theoretical SD of the MR thermometry (SDT) was evaluated from the magnitude signal to noise ratio (SNR) values [28], [29]. The magnitude SNR was calculated in the same unheated ROI as defined above. The SNR of the magnitude images was calculated using the dual acquisition subtraction method [32], [33]:where S₁ is the mean signal intensity of a non-heated ROI in the first acquired magnitude image in the liver, and SD_1–2 is the standard deviation in the same ROI in a difference image. The difference image was calculated by subtracting two consecutive GRE magnitude images. The factor in Equation 1 is necessary as the noise is derived from the difference image. For each measurement, the SNR was averaged over the acquired four slices. The theoretical SDT, assuming that white noise is the only source of error, was calculated according to Conturo et al. [30] and Salomir et al. [31] as:

Model-based temporal regularisation of the temperature data

The referenceless calculation of MRT maps cannot intrinsically reduce the temperature uncertainty below the pixel-wise SD of the measurement noise. While the referenceless MRT was chosen to filter out motion-related GRE phase shifts, an additional goal of this work consisted of evaluating the potential benefit of coupling the referenceless thermometry with a model-based regularisation as described in Kickhefel et al. [24], aiming to further improve the accuracy of thermal monitoring below the pixel-wise SD of the measurement noise. Unlike well-known low-pass temporal filtering, this approach preserves the real time feature of output information and has been shown previously to reduce the influence of artefacts occuring over short time intervals (e.g. for a few sampling points) [24], [28] when using the reference phase subtraction PRFS thermometry.

The underlying idea was to improve the MRT information of the last sampling point by considering the temporal fit predicted value (instead of the measured one), based on the past information of all previous sampling points acquired since the beginning of the procedure. This approach is meaningful here as laser-induced heating is a slow process compared to the temporal resolution of the MRT. The expanding window-based temporal prediction was applied to each newly acquired time-point. The number of sampling points included in the fit therefore linearly increases with time. This model-based temporal regularisation is compatible with real-time implementation, as the prediction is updated for each most recent sampling point. The regularisation method was applied to the referenceless values of temperature initially calculated as described above. Although the regularisation method is inherently real-time compatible, the model-constrained based regularisation was applied here to offline MRT referenceless data, for evaluation purpose, using MATLAB (Mathworks, Natick, MA, version 6.0).

The underlying physical model was derived from the 3D solution of the Pennes’ bioheat equation [25], [29] written for homogeneous tissue. In an arbitrary voxel we can write an approximated temporal solution of the bioheat-transfer-equation (BHTE) equation as a product (power of time) × (exponential factor) [24] and use it as an adjustment model in a cost-function (F) to be minimised (l₁-metrics) after each new measurement.

We consider here a small heating source, that is, the infrared light penetration depth is far smaller than the specific heat diffusion length over several minutes. An analytical solution of the Pennes’ bioheat equation, corresponding to a thin cylindrical source and written for an observation point sufficiently far away from large vessels, exists for two limit cases: (1) close to the fibre tip, written in rotation-invariant cylindrical coordinates (ρ, z):where κ is the isotropic thermal diffusion coefficient, is the in-plane distance from the heating source, t the time, and A is a constant scaled by the diffusion coefficient, and (2) far away from the tip (i.e. asymptotic solution from a small source), written in spherical coordinates (isotropic solution):where r is the radial distance from the heat source origin and B is a constant scaled by the diffusion coefficient.

In an arbitrary voxel we can write an approximated temporal solution as an intermediate situation to Equations 3 and 4 using three parameters (, , ) that are pixel-dependent:

This approximated solution was further used as an adjustment model in a voxel-wise cost-function (F) to be minimised (l₁-metrics) after each new measurement. The most recent sampling point is ranked here by the index i:

The experimentally obtained values of temperature elevation in that voxel are denoted as ; is the series of time sampling at acquisition and are the three fit parameters after i measurements (note that the cost function is minimised after each measurement, hence the index i in the parameter vector). The fit parameters minimising the cost function were used to calculate the model-based regularised temperature values at each time-point using Equation 4, see Figure 3. Additional, further prior knowledge was included in the regularisation, without reducing the generality of the algorithm. The tissue temperature is equal to the body baseline before the LITT heating started. Subsequently, we have constrained the fit model by inserting five virtual measurements forced to zero temperature elevation (i.e. the noise-free absolute temperature of body baseline) in front of the first real measured data point. Each temporal series of pixel-wise temperature to be regularised was therefore formed by five null values, followed by the actual experimental values.

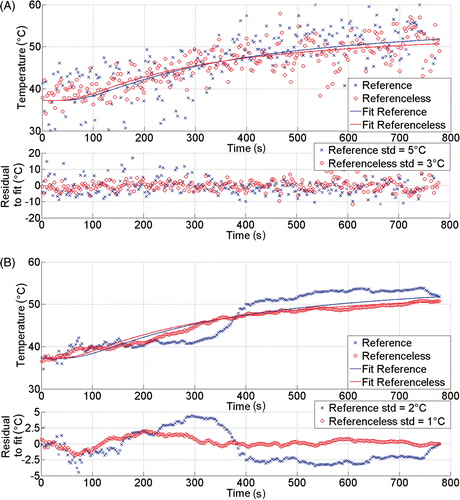
Figure 3. Illustration of pixel-wise calculation of laser-induced temperature elevation over time in the liver of patient 5. The upper frame (A) shows directly calculated values, while the lower frame (B) shows the corresponding expanding window regularised temperature data. Continuous lines are the end-point fitted curves. The reference phase subtraction and the referenceless calculation are both processed. Also, the residues between sampling point data and the end-point fitted curve are plotted below each frame. Note that the regularisation model is constrained to start at 37.2°C with horizontal tangent.

The mean SD of the residual differences between the end-point fit curve (i.e. when all sampling points of the heating period are available) and the experimental data (reference phase subtraction and referenceless MRT, independently) were calculated in order to evaluate the precision and accuracy of the two MRT methods. In addition, the SD was calculated for the residues between the end-point fit curve and the regularised data.

Analysing SD of the residual differences was a two-step process. Firstly, a pixel-wise SD of residues between a pair of temporal curves was calculated for each voxel within the ROI, resulting in a SD map characterising the whole heating period. Secondly, for each patient, a mean value of the SD map was calculated, including all ROI voxels from all slices. These calculations to evaluate the precision and accuracy of the two PRF methods were performed twice to examine the robustness of our algorithm in more detail for the heated areas. The first time all voxels in the entire region within the Dirichlet boundary were used and the second time only those voxels were used which showed an end-point temperature above 50°C.

Thermal dose calculation and prediction of ablation regions

The model-based regularised values of temperature elevation (for the referenceless technique only) were used to calculate the delivered thermal dose as described by Sapareto [34] for the cumulative equivalent minutes at 43°C (CEM43). The time-points of measurements were recorded by the MR scanner and were not, in general, regularly gridded due to the free breathing. The actual time intervals between two consecutive sampling points were taken into account in Sapareto's model.

To compare the size of unperfused area in the follow-up images (24 h after intervention) versus the size of lethal thermal dose area (based on a cut-off of 240 CEM43), the maximum and minimum diameters along two orthogonal directions were estimated in the sagittal and transversal planes. Among the three transversal slices of the MRT, the one with the largest lethal dose extension was chosen. Bland and Altman [35] analysis was applied to assess the relative contribution of the bias and error for the differences between conditions, using Stata 10 (College Station, TX) statistical software.

Results

Positioning of the LITT applicators

For all six patients, real-time temperature monitoring using the GRE with respiratory triggering was possible. No acute complications or adverse effects against Gadovist were observed. Thermometric surveillance did not interfere with planning or execution of the ablative procedure in any of the six cases. Online therapy monitoring did not lead to disruption of the procedure or replacement of applicators in any of the cases reported. There were no casualties or major complications. Minor complications comprised occasional pain sensation and self-limited peri-procedural parenchymal bleeding. Laser fibres were visualised intermittently on the magnitude GRE dynamic images as hypo-intense signal and they did not induce any artefact on the thermal map. Open sectors of the Dirichlet domain's border for referenceless MR thermometry calculation were placed on fibre tracks in three cases, on anatomical junctions in three other cases. In all six cases displayed thermal maps were consistent with therapy results as being visualised and read by the interventional radiologist.

Intrinsic SNR and baseline stability

The calculated SNR ranged from 14 to 20 for the respiratory triggered FLASH GRE acquisition of four interleaved slices per breath (see details in Table II). The standard deviation (SD) of the ‘zero’ measurement for the temperature baseline within the same unheated ROI was found to range between 2.7°C and 9.0°C using the reference phase subtraction method, and between 1.1°C and 1.8°C using the referenceless method (Table II). These latter values were found to be in the same range as the theoretical white-noise standard deviation, which indicates the excellent baseline stability of the referenceless thermometry, i.e. near the theoretical limit.

Table II.  Overview of MRT baseline stability (non-heated ROI). No temporal regularisation was performed. All data was averaged over the ROIs in all four slices. Theoretical SDT was calculated based on Equation 5.

Patient	Non-heated ROI
	Standard deviation to T = 37.2°C		SNR	White noise only theoretical STD (°C)
	STD Reference (°C)	STD Referenceless (°C)
1	3.8	1.7	14 ± 1	1.58
2	2.7	1.2	20 ± 1	1.11
3	9.0	1.6	15 ± 1	1.48
4	5.0	1.7	15 ± 1	1.48
5	3.5	1.4	18 ± 1	1.23
6	2.9	1.3	19 ± 1	1.16

The temperature baseline determined from the reference phase subtraction method with respiratory triggered GRE acquisition in this clinical scenario in liver under free breathing was prone to fluctuations far above the intrinsic ‘white noise’ SD of GRE data, indicating this method alone is not sufficiently stable for deriving a reliable thermal dose and hence a per-operatory end-point under the current conditions.

The near harmonic referenceless calculation of the temperature baselines showed a significantly higher stability, which may suggest clinical suitability of the method.

Calculation of temperature elevation around the laser applicator(s)

The laser applicator itself did not yield any measurable susceptibility artefacts (e.g. no sharp variation of the GRE phase was detected). The diffusive tip was not visible at the current resolution of the GRE magnitude images before heating (e.g. no signal void region was detected). Temperature-induced R₂* effects permitted the laser tip identification during ablation.

The benefit of monitoring the temperature with the referenceless calculation instead of the reference phase subtraction for the respiratory gated GRE acquisition is illustrated in Figure 4. The errors visible for the reference phase subtraction method increase with time, probably due to slow intra-abdominal drift of the liver shape and position [21]. As expected at the initial stage of the treatment, whenever the liver position was similar between the reference image (shown right in Figure 4) and the actual acquisition, the reference phase subtraction and the referenceless calculations yielded similar results (shown in frames 1, 2, 4 and 6 in A). However, even when the liver position appears to be similar in the reference image and an image at a later stage of heating, the reference phase subtraction leads to significant errors (shown in frames 3, 5 and 7 in B).

Figure 4. Comparison of seven consecutive acquisitions under free breathing of a sagittal plane in patient liver at two different stages of the in-progress laser ablation in patient 2: (A) temporal window approximately 4 min from starting the procedure; (B) temporal window after approximately 7 min from starting the procedure. Referenceless and reference phase subtraction MRT (shown FOV = 70 mm, relative values from baseline) and corresponding magnitude images (shown FOV = 200 mm) are presented together. Calculated relative values of temperature below − 10°C are displayed with dark blue. The circular contour overlaid on magnitude images is the inner border of the Dirichlet's domain (optionally opened). The last magnitude image of each series corresponds to the reference scan. Before laser energy is applied, the optical fibre tip is not visible in the magnitude images. A linear colour code has been used for the temperature elevation above the physiological baseline of 37.2°C.

When comparing the standard deviation of the residue between the directly calculated temperature data and, respectively, the model-based end-point temporal fit curve, the following ranges were found: from 6.6°C to 16.8°C for the case of reference phase subtraction and 1.8°C to 5.3°C for referenceless T-mapping (see Table III for details). These results indicate a higher precision for the referenceless method within the heated area by a factor of 3.3 on average. This improvement appeared to be variable from patient to patient, the six individual factors, by order, being approximately: 3.2, 1.5, 8.1, 2.9, 1.8 and 2.1. In general, a greater improvement was obtained in those cases where the initial precision of the reference phase subtraction method was low.

Table III.  Overview of model-based temporal regularisation of temperature data in the heated ROI, for the respiratory-triggered MRT acquisition sequence. All values were averaged over the ROIs in the four slices.

Patient	Diameter of ROI for temperature calculation (mm)	Percentage of open border (see Figure 2) (%)	Standard deviation of residue between end-point fitting curve and directly calculated data		Standard deviation of residue between end-point fitting curve and regularised data		Standard deviation of residue between end-point fitting curve and regularised data in pixels with end point T > 50°C
			Reference phase subtraction (°C)	Referenceless (°C)	Reference phase subtraction (°C)	Referenceless (°C)	Reference phase subtraction (°C)	Referenceless (°C)
1	75	15	16.8	5.3	4.6	1.5	5.2	2.1
2	60	20	6.6	4.4	3.4	2.1	4.3	2.9
3*	75	15	14.6	1.8	10.2	0.7	15.2	1.2
4	90	20	8.9	3.1	1.9	0.8	2.2	1.2
5	60	20	8.1	4.4	3.8	2.2	4.4	2.8
6	60	20	7.8	3.7	3.1	1.4	3.9	1.9

*Patient 3 responded less effectively to sedative medication, yielding significantly higher inter-breathing variation of the baseline GRE phase.

The real time regularisation (i.e. expanding window temporal filtering) based on the BHTE model [28] significantly improved the precision of the temperature estimation in all cases, for both methods separately (Figure 3 and Table III). As the past information of the slow temporal process was included in the actual temperature prediction, the regularised values of temperature showed decreased spreading around the end-point fitting curve. When the model-based regularisation was applied to the reference phase subtraction MRT data, the standard deviation of the regularised residues around the fitting curve ranged from 1.9°C to 10°C (entire region within the Dirichlet boundary)/2.2°C to 15.2°C (only pixels with end-point absolute temperature above 50°C), whereas the same correction algorithm working on the referenceless calculation output data leads to residues of standard deviation ranging from 0.7°C to 2.1°C (entire region within the Dirichlet boundary)/1.2°C to 2.9°C (only pixels with end-point absolute temperature above 50°C). Note an approximately four-fold average increase in precision between the two MR thermometry methods also for the entire Dirichlet's domain as for specific pixels with end-point absolute temperature above 50°C. In the latter situation, the SDT is 30–50% higher than for the entire region average, because of the inherent GRE signal loss by intra-voxel phase dispersion in the presence of strong temperature gradients (via the PRFS effect).

As illustrated in Figure 3A, the deviations between the pixel-wise referenceless MRT values and the corresponding model-based fit curve tend to increase with time (while the corresponding regularised values closely follow the fit curve in a stable manner over time). This gradual increase of pixel-wise deviations of unregularised referenceless MRT values are explain by two reasons: (1) local heating decreases the magnitude of the GRE signal by intra-voxel phase dispersion mechanism and subsequently the ‘white’ noise increases (that is, the local temperature gradient and the PRFS effect mimicking decrease), and (2) the thermal build up is moving ‘randomly’ through the observed pixel as there are residual motion errors in the order of millimetres with free breathing triggering (mainly along the HD direction, see also Figure 3). That is, the observed pixel is falling into slightly different regions of the tumour. The higher the local temperature gradient, the higher the span of observed fluctuations.

Spatial correlation between thermal dose and post-treatment unperfused regions

The spatial correlation between the ablation regions (as predicted from the thermal dose calculation with regularised referenceless MRT) and the 24 h post-treatment unperfused regions was found to be excellent, see Table IV and Figure 5. The Bland and Altman test indicated:

• in the transverse plane: lethal thermal dose versus unperfused areas size difference 1.46 ± 2.10 mm with 95% LOA (−2.67; 5.58) mm,

• in the sagittal plane: lethal thermal dose versus unperfused areas size difference 0.96 ± 2.46 mm with 95% LOA (−3.87; 5.79) mm.

Table IV.  Spatial correlation between the size of the unperfused region (24 h post-treatment) and the predicted ablation (240CEM43) from regularised reference-less thermometry data.

	Transversal plane		Sagittal plane
Patient	Unperfused region at 24 h post-treatment (mm × mm)	240CEM43 thermal dose region (mm × mm)	Unperfused region at 24 h post-treatment (mm × mm)	240CEM43 thermal dose region (mm × mm)
1	43 × 43	47.5 × 42.5	41 × 40	45 × 37.5
2	33 × 31	35 × 30	31 × 29	30 × 30
3	49 × 42	50 × 45	48 × 44	50 × 45
4	40 × 35	42.5 × 35	41 × 32	40 × 35
5	48 × 31	47.5 × 30	53 × 31	50 × 32.5
6	50 × 40	52.5 × 45	50 × 41	55 × 42.5

Note, the thermal dose calculation showed a minor tendency to overestimate the actual unperfused region, but given the voxel size of 2.5 mm in the plane, these differences are not statistically significant (i.e. average overestimation of lesion diameters similar to half a voxel).

Discussion

The MR sequences and set-up, as well as the data processing algorithms for computing PRFS temperature maps, should be designed specific to the target organ. In particular, a fundamental difference exists between monitoring moving and non-moving organs. The reference phase subtraction PRFS method works accurately for non-moving organs. For example, an excellent precision of 0.2°C can be achieved in brain MRT with the head immobilised [36]. Any misregistration between the reference and actual images induces an over- or underestimation of the calculated temperature. The worst case is the unique event (i.e. non-predictable) motion, such as accidental muscle contraction, peristaltic drift of abdomen organs, or swelling/shrinking of tissue induced by the treatment itself. Temperature errors induced by non-predictable motion cannot be recovered by a multi-baseline [15], [18], [19] approach.

Referenceless PRFS thermometry [20] is intrinsically insensitive to both periodic and unique event tissue motion if some specific border conditions are fulfilled. The previously reported implementations interpolate the spatial information from a rectangular, closed, thick border towards the inner ROI. It may be challenging to place this type of border (additionally required to be unheated and free of artefacts) around the area to be treated in a patient. The l₁-metrics variant [22] relaxes the constraints for the border, but behaves as a spatial high-pass filter and therefore works accurately only for small heated areas. Contrarily, in laser ablations, the heated region is large (several cm in size) and the heating regime may frequently exceed 70°C tissue temperature. Note, neither multi-reference nor referenceless approaches can filter out intra-scan motion artefacts (e.g. ghosting along phase encode direction). Nevertheless, in most cases artefacts induced by intra-scan motion are negligible against inter-scan motion artefacts.

Furthermore, referenceless temperature monitoring expands the workflow flexibility. The heat source can be repositioned or additional heat sources could be placed without the time-penalty induced by re-mapping the atlas of tissue motion. The multi-baseline technique is still a time-referenced calculation and requires a waiting period for tissue cooling before starting a new session of temperature monitoring if the slice orientation has changed. Unlike the multi-reference approach, the slice position and orientation may be varied during the intervention unconstrained to some a priori mapped space of events when using the referenceless approach. As thermal dose computation is a time-integrating process, the plan of acquisition should ideally track the tumour's frame motion, to enable continuous monitoring of the same anatomy.

Our approach is based on a novel referenceless PRF method using a thin, open, and circular border around the heating target area. To the best of our knowledge, this is the first clinical study when referenceless PRFS thermometry is applied to MR data acquired during thermal ablation on liver malignancies under free breathing. This approach is demonstrated to be compatible with a lower risk procedure avoiding general anaesthesia and controlled ventilation. Moreover, this is the first clinical study comparing the thermal dose prediction versus post-treatment assessment of liver ablation when referenceless PRFS thermometry is involved.

The calculation of the GRE background phase was based here on the solution of the 2D-restricted Dirichlet problem, hence avoiding the practical difficulty in acquiring time resolved 3D MR volumes on mobile organs. The user has to define the closed or open border once (at the beginning of the procedure), and later redefinition is required only in the case of slice repositioning. No other user interaction is required. Particular care should be taken, however, to avoid expansion of the heated anatomical region to the Dirichlet's domain border, which would violate the underlying border condition of no change in temperature. Utilising a border gap may help to reduce this risk.

The approach, combining free breathing conditions (hence obviating the general anaesthesia), respiratory triggered GRE acquisition, near-harmonic referenceless PRFS MR thermometry and model-based real-time compatible regularisation of temperature values, yielded an estimated precision ranging from 0.7°C to 2.1°C with an average in six patients of 1.45°C). This resulted in millimetre-range agreement between the calculated thermal dose and the 24 h post-treatment unperfused regions in liver in the transverse and sagittal planes. Our results also suggest that the described approach provides sufficient precision to be used as a safety tool and prevent un-prescribed thermal lesions during local thermal therapy.

The model-based regularisation increases the actual precision of measurement without decreasing the temporal resolution, whilst not compromising the real-time capability of the method as the filtered values propagate one sampling point forward at each measurement. Since input data for the regularisation filter is motion-robust (i.e. referenceless MRT measurements), so does the regularised data. When small irregularities of the respiratory triggers exist, each temperature value is inherently correct (referenceless calculation), but a pixel-wise temporal curve is constructed from different liver cells (or mass points) fluctuating around an average position. The model-based regularisation is smoothing out the effect of small positional fluctuations of a true tissue mass point around a given pixel in the image.

Model-based regularisation of high temporal resolution data is suitable especially when feedback control of the therapy is envisaged and therefore the effective dwell time is a critical parameter. Theoretically, when a slow heating process is applied with open loop (i.e. monitoring only), another meaningful approach would be to decrease the temporal resolution and increase the intrinsic SNR, which converts into a lower SD of thermometry (i.e. acquisition of one slice only per breath with multiple cycles required to complete one multi-slice stack, instead of acquiring multiple slice stacks per breath).

Several recent clinical studies addressed the issue of the thermal dose versus ablative lesion correlation in MR-guided RF ablation, systematically using controlled breathing and general anaesthesia. They reported large and systematic overestimation of the true lesion size by the thermal dose-based prediction derived from continuous MRT during ablation in the transverse plane with bias mean 11.44 mm ± 3.8 mm SD for the maximum diameter and 7.33 ± 7.14 mm for the minimum diameter [37], and the absence of correlation when the imaging plane orientation varied [38]. These effects are due to thermal cavitation, yielding water steam bubble formation above 100°C in the vicinity of the RF electrode and producing dynamic changes of tissue susceptibility [39]. Threshold-based prediction of the coagulation zone in sequential temperature mapping in MR-guided RF ablation of liver tumours, that is, fractionary application of RF energy interleaved with PRFS tissue measurement, improved the predictive value [40]. Under a similar acquisition paradigm, the referenceless calculation of temperature would require the initial correction for the static susceptibility artefact of the electrode. Here, the infrared energy deposition was distributed approximately uniformly along the 30-mm long diffusive tip and the actual power per applicator ranged between 8 and 14 W, as compared to 30 to 120 W for RF electrodes [39]. The measured temperatures did not exceed the absolute temperature of 90°C in our study, therefore no susceptibility disruptive phenomena were observed. Overall we report 1 to 1.5 mm systematic agreement between lethal thermal dose map and the unperfused region (Table IV).

The assessment of the matching between the ablation region and the initially assigned tumour volume was not defined as an objective of this study, nor was correlating the accuracy of the thermal targeting with the patients outcome. The purpose of this work focused on evaluating, under clinical conditions, the capability of correctly measuring the temperature elevation in liver and subsequently accurately predicting the irreversible thermal damage.

The referenceless PRF method demonstrated to be feasible in our pilot study aims to help to achieve clinical standards in monitoring thermal therapy, but is not yet sufficient to enable a clinical routine use. The placement of the border remains difficult in certain cases and requires detailed analysis and profound experience; for example, when the target region is near the liver capsule or if large vessels are nearby. If temperature elevation or artefacts interfere with a ROI's border, the temperature calculation is expected to result in an over- or underestimation. A circular geometry may be limiting for the referenceless method, for instance when the heating area is long and narrow, as in such cases the background phase calculation would include many pixels out of interest for temperature calculation. Future work should address the question of using an arbitrary border defined automatically (i.e. user-interaction-free) for an improved practicability and flexibility.

Conclusion

A referenceless PRFS thermometry method based on the theoretical framework of harmonic functions was applied to clinical data acquired during MR-guided laser ablation of liver malignancies in consciously sedated, freely breathing patients. Millimetre-range agreement was obtained between the calculated thermal dose and the 24 h post-treatment unperfused regions in the liver. The current referenceless MRT approach expands the workflow flexibility and is insensitive to unique event motion and to swelling or shrinking of heated tissue. Further technical developments are required to enable the routine use of this novel referenceless PRFS thermometry method in clinics.

Declaration of interest: The authors report no conflicts of interest. The authors alone are responsible for the content and writing of the paper.

Appendix

This section details the physical, mathematical and numerical aspects of the near-harmonic referenceless MRT method and summarises the basic phantom studies performed prior to its application on patient data.

Theory

To recall the foundation principle, the baseline GRE phase map (denoted here as ) can be described as a harmonic function (that is, null Laplacian value) in regions with homogeneous or linearly changing magnetic susceptibility.During the thermal intervention, the background phase, which excludes temperature-induced phase shifts, can be extracted from the acquired phase map by solving a classic Dirichlet-type problem [23], [41]. Subsequently, a temperature map can be calculated from a single time-point phase measurement by subtracting the reconstructed background phase.

Equation A1 describes a 3D problem. For carrying out real-time MR monitoring simultaneously to minimally invasive therapies it is convenient to reduce the 3D problem to a 2D problem. This reduction can be performed by describing the second spatial derivation in the third dimension by an average constant value, denoted as . We further denote the continuous 2D in plane coordinates as . To determine the 2D background phase the following 2D Dirichlet problem must be solved:where represents the measured phase map.

The Dirichlet problem was numerically solved using an iterative approach based on a 5-pixel discretisation of Equation A2 with 2D indexes (i, j):

The approximated solution can be propagated from iteration (n) to (n + 1):Iterations are repeated up to a rank N such that no significant changes occur between and .

The theoretical and numerical framework described above is valid for any shape of the connex domain . In particular, a circular geometry is a convenient choice, which enables rapid and direct calculation of the average residual value of the 2D phase's Laplacian (ϵ). This can be estimated by using a double circular border of radii and, respectively, pixels [23], [41]:The recommended value for is 2, as a compromise between the border thickness (equal to ) and the robustness of contrast-to-noise ratio in the calculation of ϵ.

MRgHIFU sonication in moving phantom

Focus ultrasound heating was produced using a 256-element phased array transducer (Imasonic, Besançon, France) with aperture D = 140 mm, natural focal length R = 130 mm and nominal frequency range from 968 kHz to 1049 kHz. The phased array was driven by a programmable 256-channel generator (Image Guided Therapy, Pessac-Bordeaux, France) with independent control of amplitude and phase per channel, and was moved in the horizontal plane (Ox and Oz axes in the magnet frame) by a 2D positioning system with piezoelectric actuators (Image Guided Therapy, Pessac-Bordeaux, France).

Single slice MR thermometry acquisitions (in coronal plane, through the HIFU focal point) were performed on a 3T whole body MRI scanner (Magnetom Trio, A Tim system, Siemens, Erlangen, Germany) with maximum gradient strength 45 mT/m and slew rate 200 T/m/s. The PRFS-sensitive sequence was based on the gradient-echo planar imaging (GRE-EPI) kernel with main acquisition parameters: FOV 128 × 128 mm², 1 coronal slice, voxel size 1 × 1 × 5 mm³, TR 20 ms, TE 8.2 ms, echo spacing 1.16 ms, EPI factor 9, partial Fourier 6/8, flip angle 10°, bandwidth 1002 Hz/Px, fat suppression, body matrix coil with six elements.

Experimental simulation of the respiratory motion was obtained by using an inflating balloon driven by a mechanical ventilator (Servo Ventilator 900D, Siemens-Elema, Solna, Sweden), as shown in Figure 6. The balloon was circumscribed by five faces of a parallelipedic support, while in the direction of the missing sixth face of the support the balloon was in contact with an US transparent bag containing degassed ex vivo liver tissue. The amplitude of the periodic motion while inflating/deflating the balloon ranged from 1 to 3 cm depending on the air volume injected by the ventilator. The main direction of motion was HF and the period of motion was adjusted within the range of 4 to 7 sec/cycle. An appropriate acoustic window from the HIFU transducer enabled the ex vivo tissue to be sonicated, as visible in Figure 6. Interleaved double focus HIFU sonication (50%–50% duty cycle, 6 mm inter-foci gap along LR direction, 500 ms repetition time) was performed continuously in the moving sample for 40 s, with each focus position fixed.

Figure 5. (A) Visual comparison between thermal dose 240CEM43 threshold and the Gd-uptake 24 h follow-up. Contrast enhanced FLASH 2D magnitude images acquired 24 h after intervention are shown. They are overlaid by the threshold border of the lethal thermal dose. (B) Bland and Altman graphics for the same data.

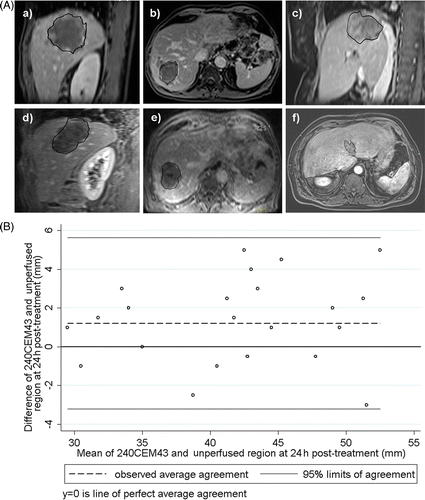
Figure 6. Ex vivo simulator of breathing motion during MRgHIFU therapy. An inflating balloon (1) is driven by a mechanical ventilator and induces motion of the ex vivo specimen (3). The HIFU transducer (2) is positioned by means of a 2D piezoelectric motorised system (4). The air flow into the balloon is indicated by the black arrow.

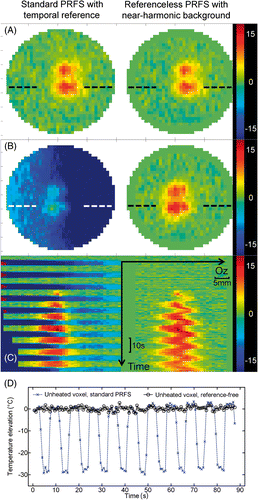
The stability of the reference-free method was demonstrated in moving phantoms, as illustrated in Figure 7. The mechanical ventilator-driven balloon inflated and deflated in an approximately binary manner, i.e. high/low states with rapid transition. The reference for the standard PRF was defined as the average phase image of four successive rapid acquisitions during the first high level state. Therefore, it was possible to compare the results of standard PRF thermometry and the new reference-free method each half period when the balloon was inflated (i.e. high-level state). Under this condition, both methods provided similar values of temperature, within the intrinsic noise standard deviation. Contrarily, during low-level states (e.g. deflated balloon), the standard method yielded large errors, in particular the underestimation of the temperature by several tens of °C, whereas the reference-free method correctly tracked the temperature evolution in the displaced tissue, see the stable baseline in Figure 7D.

Figure 7. Ex vivo moving phantom comparison between reference phase subtraction PRFS thermometry (B_o-drift corrected) and the reference-less calculation using the near-harmonic reconstruction of the background phase. Results are shown for an interleaved double focus HIFU sonication of 40 s (50%–50% duty cycle, 6 mm gap along LR direction, 500 ms repetition time). The imaging plane was orthogonal to the HIFU beam axis (shown FOV is 41 mm square). The set-up shown in Figure 3 has been used, adjusting the ventilation period at 7.5 s. The implementation of the reference-free calculation used a closed circular border of inner radius 16 pixels (16 mm). (A) coronal temperature change maps after 24 s of sonication, inflated balloon state; (B) coronal temperature change maps after 27.4 s of sonication, deflated balloon state; (C) colour coded 1D profile of temperature change through one focal spot (see dotted line in frames A and B), scrolled over time. The temperature change colour bars are gridded in °C; (D) plot of the calculated temperature with time for the two MR thermometry methods in the same unheated voxel; note the periodic large error of standard PRFS calculation and the stable baseline for the reference-free method.