Bipolar radiofrequency ablation with four electrodes: Ex vivo liver experiments and finite element method analysis. Influence of inter-electrode distance on coagulation size and geometry

Abstract

Purpose: The aim of this study was to develop an electrode system with simple needle electrodes which would allow a reliable and predictable ablation zone with radiofrequency ablation (RFA).

Materials and methods: In the first step, four parallel electrodes (active length 3 cm, diameter 1.8 mm) were inserted in ex vivo bovine liver. A power of 50 W was applied between two pairs of electrodes for 10 min or until current shut-off due to impedance rise. In the second step, the influence of changing inter-electrode distance on coagulation size and geometry was measured. In the third step, a finite element method (FEM) analysis of the experiment was performed to better understand the experimental findings.

Results: A bipolar four-electrode system with templates adjusting the inter-electrode distance was successfully developed for ex vivo experiments. A complete and reliable coagulation zone of a 3 × 2 × 2-cm block was obtained most efficiently with an inter-electrode distance of 2 cm in 5.12 ± 0.71 min. Above 2 cm, coagulation was incomplete due to a too low electric field, as demonstrated by the FEM analysis.

Conclusions: The optimal inter-electrode distance of the present bipolar four-electrode system was 2 cm, allowing a reliable and predictable ablation zone in ex vivo liver. The FEM analysis correctly simulated and explained the findings in ex vivo liver. The experimental set-up may serve as a platform to gain more insight and to optimise the application of RFA by means of four or more simple needle electrodes.

• bipolar
• experimental
• finite element method
• liver
• radiofrequency ablation

Introduction

Over the last 10 years, numerous types of RFA electrodes have been developed [1]. Current electrodes have a complex design to enhance the ablation zone and they are expensive (€1000/US$1300 or more). The main goal in the development of these electrodes has been to achieve ever larger ablation diameters, while attention to reliability has lagged behind. With current electrodes, large ablation zones can be obtained but their predictability and completeness is problematic. Size and shape of the ablation zone is highly variable and difficult to predict even with the most recent electrodes [2–10]. Local recurrence rates in clinical studies remain as high today as they were 10 years ago, especially in tumours >3 cm [11]. Incomplete ablation not only leads to local recurrence but may render a tumour even more aggressive than before [12], [13]

The aim of this study was to develop an electrode system which would allow a more reliable and predictable ablation zone. Therefore, we went back to the simple needle electrodes from the early years of RFA. Bipolar RFA in the liver between simple needle electrodes has been studied only in one of the first papers on RFA in the liver [14]. Current was applied between two parallel electrodes. The resulting coagulation zone, however, was butterfly shaped and therefore not clinically useful, and the concept was abandoned for many years. In these experiments, we returned to this idea and tried to optimise an electrode system consisting of four parallel simple needle electrodes used in a bipolar mode in order to obtain a reliable and predictable ablation zone.

Materials and methods

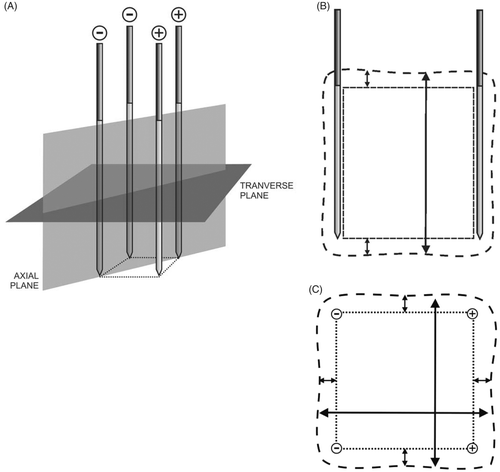
Experimental set-up (figure 1)

The experiments were performed on freshly excised beef liver (7 to 10 kg) that was allowed to acquire room temperature overnight. On the day of the experiments, the liver was placed in a shallow plastic container that rested on the surface of a large plastic container with water at a constant temperature of 20°C in order to minimise temperature changes in the liver due to local radiofrequency (RF) heating.

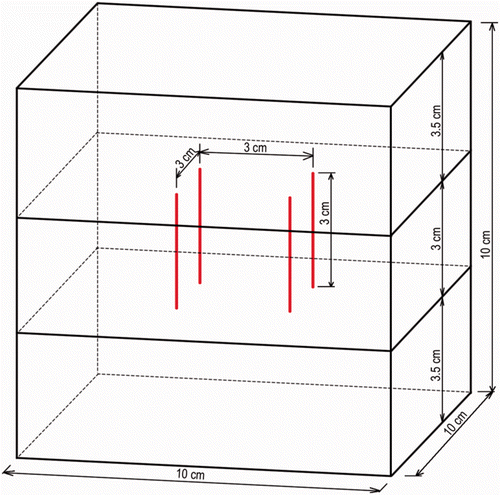
Four parallel simple needle electrodes (Kirschner wires, Devroe Instruments, Vichte, Belgium) with a 1.8 mm diameter and electrically insulated by a plastic sheath over their entire length except for the last 3 cm at the tip (defined as the active part of the electrode) were introduced into the liver in a square configuration. Placement near large vessels (portal vein, hepatic veins) was avoided. Parallelism and precise spacing between electrodes were obtained by introducing them through a 3.2-cm thick multi-perforated Polyoxymethylene block, allowing inter-electrode distances of 1, 1.5 and 2.5 cm and their multiples.

Temperature was monitored with a thermocouple embedded in a Tyco single 15 cm Cool-tip® electrode (length 15 cm, active tip 3 cm), which was inserted in the centre of the square configuration, with its tip in the plane created by the tips of the four RF electrodes (Figure 1).

Figure 1. (A) Experimental set-up; (B) Experimental set-up, electric wiring scheme: ○ electrode; • thermocouple.

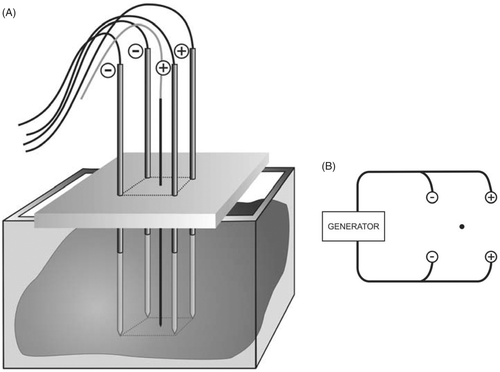
Electrodes were activated by a Tyco CC-1 generator (Tyco Healthcare, Mechelen, Belgium) with a maximal output of 200 W. A bipolar current field was established between the first pair of ‘positive’ electrodes and the second pair of ‘negative’ electrodes. Power was applied for 10 min or until current shut-off due to impedance rise. A fixed power level of 50 W was chosen, based on pilot experiments. Fixed power rather than fixed current or voltage was chosen so that energy deposition in the tissue per time was equal for all experiments.

The inter-electrode distances applied in this study were: 1.0, 1.5, 2.0, 2.5, 3.0 and 4.0 cm. For each experimental setting, 6 ablations were created.

Ablation protocol

The bipolar four electrode system was tested using the following fixed parameters:

• electrode diameter: 1.8 mm

• power: 50 W

• duration: 10 min or until current shut-off due to impedance rise

The following parameters were recorded just before the experiment, each minute during the experiment and immediately after the experiment: impedance, current, temperature and time of current shut-off.

Measurement of ablation zone size (figure 2)

The ablation zone was measured in line with the standard description of single electrode ablation zones [15]. In summary, the electrodes were left in place until the liver was sectioned. A large cube of liver containing the electrodes and the expected coagulation zone was cut out from the rest of the liver. This liver cube was first cut in the axial plane parallel to the electrodes, determined by the right upper and left lower electrode of the square configuration (Figure 2A).

Figure 2. (A) Measurement of the ablation zone size, definition of planes. (B) Measurements in the axial plane: - - - - rectangle defined by the active parts of the electrodes; – – – – coagulation zone; small arrows, axial margins outside this rectangle; large arrow, axial diameter. (C) Measurements in the transverse plane: ···· square defined by the active parts of the electrodes; – – – coagulation zone; small arrows, lateral margins outside this square; large arrows, transverse diameters.

All measurements included the central tan-white zone, which feels firm when touched and which corresponds to irreversibly damaged tissue, and excluded the reddish transition zone, which has the same weak consistency as the surrounding normal liver tissue and which corresponds to viable tissue on histochemical staining [15], [16].

The following dimensions of the coagulation zone were measured in the axial plane (Figure 2B):

• minimal and maximal axial margin: minimal and maximal distance between plane of distal ends of the electrode tips and coagulation zone and between the plane of the proximal ends of the electrode tips and coagulation zone

• minimal and maximal axial diameter: minimal and maximal distance between proximal and distal border of the coagulation zone

• completeness of ablation: ‘complete’ meaning that the whole area circumscribed by the electrode tips laterally, the plane between the proximal ends of the electrode tips and the plane between the distal ends of the electrode tips was completely coagulated; ‘incomplete’ meaning that fusion between coagulation zones around each electrode was only partial or absent.

After the measurements in the axial plane, the two halves were cut in the transverse plane, perpendicular to the electrodes, at mid-distance of the electrode tip (Figure 2A). The lower halves were reassembled.

The following dimensions of the coagulation zone were measured in the transverse plane (Figure 2C):

• minimal and maximal transverse margin: minimal and maximal distance between each of the four sides of the square determined by the electrodes and the respective border of the coagulation zone

• minimal and maximal transverse diameter: minimal and maximal distance between two opposite borders of the coagulation zone

• completeness of ablation: ‘complete’ meaning that the whole area within the square determined by the electrodes was completely coagulated.

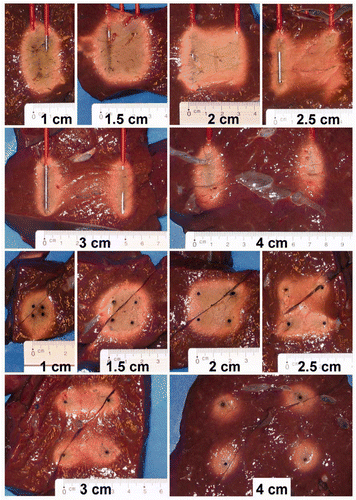
A picture of the coagulation zone in the axial and in the transverse plane was taken for each experiment.

Statistical analysis

Numerical data were reported as mean ± standard deviation (SD). A multivariate analysis of data was carried out to take into account the simultaneous influence of various factors such as inter-electrode distance, power, electrode diameter and electrical mode (some of these factors will be analysed in subsequent papers). Duration of coagulation, end temperature, time and coagulation speed (numerical data) were analysed by linear regression, and completeness of ablation (dichotomous data) by logistic regression. Regression analysis of repeated measures using generalised estimating equation (GEE) was performed to study the values of temperature, impedance and current at every minute. Student's t-test was used for some particular comparisons. A P value less than 0.05 was considered as statistically significant. Statistical analysis was performed using SPSS 15.0 statistical software (Chicago, IL, USA).

Finite element method analysis (figure 3)

In order to further understand the influence of inter-electrode distance on coagulation size and geometry, we performed a finite element method (FEM) analysis using our home-made FEM software specially developed for RFA simulation, RAFEM [17]. RAFEM allows more flexibility than commercially available software such as ABAQUS [18], FEMLAB [19], ANSYS [20] or COMSOL Multiphysics [21].

Two partial differential equations are involved. The first is a continuity equation which allows the calculating of the electric potential V at any point of a volume, with σ being the electric conductivity (unit: siemens per metre):

For simplification, the alternating current of 500 kHz is considered as a direct current. This assumption has been commonly accepted in literature about mathematical modelling of RFA [22].

The second equation is a modified Pennes’ heat transfer equation for temperature T in which the terms describing heat transfer by convection (blood perfusion) and heat generation by metabolic processes have been omitted and to which a term describing heat generation by the electric current (j · E) has been added:

In Equation 2, ρ denotes density (kg/m³), c is heat capacity (J/kg · K), k stands for heat conduction coefficient (W/K · m), j means electric current density (A/m²) and E is the electric field (electric potential gradient) (V/m). The last term represents the Joule heating. As the electric current density j is equal to the product of the electric conductivity σ and the electric field E, the Joule heating is proportional to the square of the electric field. This equation is an accurate mathematical model of RFA of the ex vivo liver in which blood flow and metabolic processes are absent.

The geometrical model that was used is a box of 100 × 100 × 100 mm, as shown in Figure 3. Two pairs of cylinders, standing for two pairs of electrodes of opposite polarity, with a diameter of 1.8 mm and a length of 30 mm, are embedded at a depth of 35 mm beneath the top surface.

Figure 3. Geometrical model for FEM analysis.

As boundary conditions, zero voltage was set on the left pair of cylinders. To the right pair of cylinders, we applied a voltage determined in such a way that the power input into the model was equal to 50 W. It was assumed that the heat flux vanished along all the boundaries. The initial temperature of the model was defined to be 20°C. Thermal and electrical properties of normal liver were taken from Tungjitkusolmun et al. [22] (Table I). As a simplification, electrical and thermal conductivity were considered as temperature independent. The 50°C isotherm was used to predict the ablation zone [23–27].

Table I.  Thermal and electrical properties of liver and electrode [22].

Name	Symbol	Unit	Values
			Liver	Electrode
Density	ρ	kg/m^3	1060	6450
Specific heat	c	J/kg · K	3600	840
Heat conductivity	k	W/m · K	0.512	18
Electric conductivity	σ	S/m	0.333	1 × 10^8

Results

Influence of inter-electrode distance (figure 4, and 5)

With increasing inter-electrode distance, several phenomena were noted:

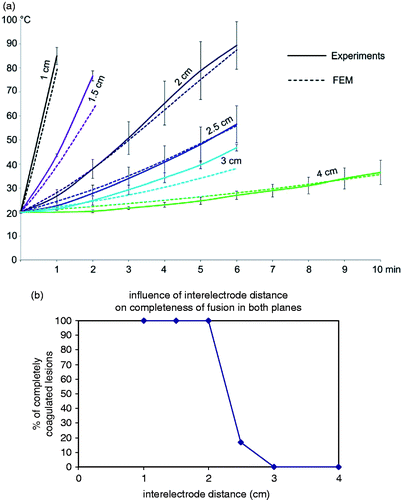
• Temperature build-up was slower (p < 0.001) and end temperature was lower (p < 0.001). The threshold temperature of 50°C was not reached when inter-electrode distance was 3 cm or more (Figure 4A).

  Figure 4. (A) Influence of the inter-electrode distance on temperature as measured during experiments or predicted by FEM. (B) Influence of the inter-electrode distance on completeness of ablation in both planes.

  

• Ablation in both the axial and the transverse plane was always complete up until an inter-electrode distance of 2 cm and was often incomplete above 2 cm (p = 0.005) (Figure 4B and 5). With increasing distance above 2 cm, incomplete coagulation in the transverse plane was observed first in the plane half way the two positive electrodes on the one hand and the two negative electrodes on the other hand, and then in between all four electrodes (Figure 5).

  Figure 5. Influence of the inter-electrode distance on the coagulation zone in the axial and transverse planes.

  

• An inter-electrode distance of 2 cm allowed the quickest complete coagulation per cm³ of the tissue in between the boundaries of the four electrodes (0.42 cm³/min, 1.44 cm³/min and 2.29 cm³/min, for an inter-electrode distance of 1, 1.5 and 2 cm respectively) (p < 0.001).

Ablation process at the optimal inter-electrode distance of 2 cm (figure 6, table II)

At the optimal inter-electrode distance of 2 cm, temperature went up very smoothly. Impedance first decreased during the first 3 min, then increased from min 4 on until a sudden impedance rise occurred with current shut-off. With constant power output of 50 W, current first increased during the first 3 min, then decreased from min 4 on until impedance rise with current shut-off.

The ablation process took 5.12 ± 0.71 min until current shut-off. End temperature was 77.7 ± 12.4°C. Coagulation was complete in both the axial and the transverse plane. Dimensions are given in Table II.

Table II.  Dimensions of the coagulation zone with standard set-up: Experimentally measured (mean ± SD (range)) vs. predicted by FEM.

	Experiment	FEM
Minimal axial margin (mm)	1.6 ± 1.4 (0–4)	6.1
Maximal axial margin (mm)	4.3 ± 1.8 (2–8)	9.5
Minimal axial diameter (mm)	35.5 ± 1.2 (34–37)	42.2
Maximal axial diameter (mm)	41.5 ± 2.1 (40–45)	47.6
Minimal transverse margin (mm)	5.7 ± 1.3 (3–9)	8.1
Maximal transverse margin (mm)	7.1 ± 2.2 (3–11)	11.9
Minimal transverse diameter (mm)	31.6 ± 3.1 (25–36)	36.2
Maximal transverse diameter (mm)	34.3 ± 3.6 (30–41)	43.8

Finite element method analysis

The experimentally measured and numerically predicted transient temperatures matched closely (Figure 4A). The 50°C isotherms calculated by RAFEM were similar in shape to the borders of the ablation zones observed in our experiments, although RAFEM overestimated the experimental ablation diameters by about 5 mm (Table II).

The magnitude of the electric field (electric potential gradient) (V/m) in the transverse plane at the mid-height of the electrodes is represented in Figure 7(A). The electric field is strongest horizontally between the positive and the negative electrodes and is much weaker in the plane halfway between the two couples of a positive and a negative electrode.

Figure 6. Evolution of impedance and temperature with the standard set-up: 50 W power, 2 cm inter-electrode distance, 1.8 mm diameter electrodes (mean ± SD).

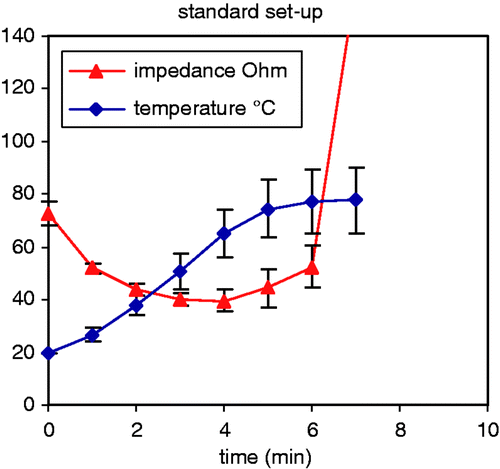
Figure 7. (A) Electric field in the transverse plane at the mid height of the electrodes applying 50 W with an inter-electrode distance of 3 cm. (B) Temperature (°C) after 7 min of RFA in the transverse plane applying 50 W with an inter-electrode distance of 3 cm. ––– 50° isotherm; - - - - 60° isotherm.

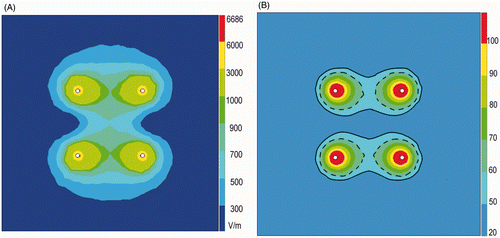
Figure 7(B) shows the 50°C isotherms calculated by RAFEM when applying 50 W for 7 min with an inter-electrode distance of 3 cm. They appear as two separated band-like zones, very similar in shape to the borders of the coagulated zones observed in our experiments, as shown in Figure 5.

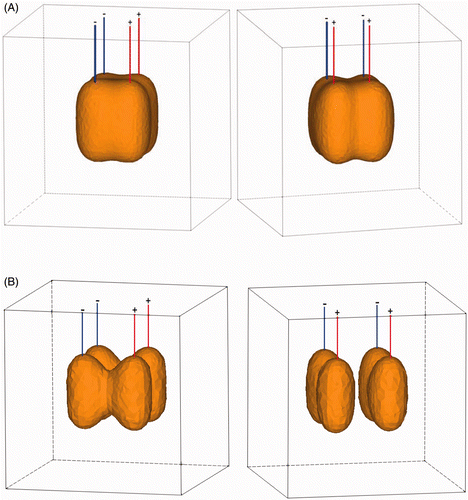
Figure 8 shows a 3D representation of the 50°C isotherm after 7 min of RFA applying 50 W with an inter-electrode distance of 2 cm (Figure 8A) and 3 cm (Figure 8B). Ablation is complete with an inter-electrode distance of 2 cm, as it entirely covers the rectangular volume in between the active parts of the four electrodes. Ablation is incomplete to non-existent with an inter-electrode distance of 3 cm.

Figure 8. (A) 3D representation of 50°C isotherm after 7 min of RFA applying 50 W with an inter-electrode distance of 2 cm (left: front view; right: side view). (B) 3D representation of 50°C isotherm after 7 min of RFA applying 50 W with an inter-electrode distance of 3 cm (left: front view; right: side view).

Discussion

The aim of this study was to develop an electrode system which would allow a reliable and predictable ablation zone. Therefore, we went back to the simple needle electrodes from the early years of RFA. Bipolar RFA in the liver between simple needle electrodes has been studied in one of the first papers on RFA in the liver [14]. Current was applied between two parallel electrodes. The resulting coagulation zone however was butterfly shaped and therefore not clinically useful, and the concept was abandoned for many years.

Monopolar RFA in the liver with four simple needle electrodes has also been studied in one succinct study [28]. The electrodes were used in a simultaneous and monopolar mode. The resulting coagulation zones were also disappointing because of incomplete coagulation as soon as the electrodes were spaced apart more than 1.5 cm.

Since then, multiple electrodes and the bipolar mode have been tested with novel design electrodes (wet, cooled, expandable, bipolar on a single shaft and various combinations [1]) but never again with simple needle electrodes until the description of the Habib sealer [29]. The Habib sealer consists of four simple needle electrodes with a 4-cm active tip, with a narrow inter-electrode distance of 5 mm. This device has been designed to coagulate a plane, i.e. a small rim of liver tissue in the future transsection plane. The use of a bipolar four-electrode system to coagulate a predefined volume of liver tissue has to our knowledge not been reported before.

In our study, the coagulation zone using an inter-electrode distance of 2 cm proved to be very reproducible and complete. The coagulation zone was remarkably homogenous, without the typical carbonisation which is often seen in RFA using other electrodes (Figure 5). The rectangular shape of the coagulation closely matched the rectangular shape of the volume in between the active parts of the four electrodes, extending 2.9 ± 2.1 mm (range 0–8) beyond this volume in the axial plane and 6.4 ± 1.9 mm (range 3–11) in the transverse plane (calculated on both the minimal and the maximal measurement in each plane). Coagulation was quick (5.12 ± 0.71 min). The transient decrease of impedance in the first part of the ablation process was due to increased electrical tissue conductivity due to heating [30]. It was followed by a gradual rise of impedance due to dehydration.

The discovery that complete coagulation was found for an inter-electrode distance up to 2 cm but not above is valid only for the setting of the experiment, i.e. an electrode diameter of 1.8 mm with a fixed power output of 50 W, applied for 10 min or until current shut-off due to impedance rise.

Can a complete coagulation be obtained with an interlectrode distance above 2 cm by using higher power or a longer duration? We studied this question in another set of experiments, which will be discussed in a separate paper (data not shown). The main result of these additional experiments is that it is hard to obtain complete coagulation with an inter-electrode distance above 2 cm.

Increasing power output for higher inter-electrode distances is not a solution. A power of 60 W gives similar results to a power of 50 W but power values above 60 W only lead to even quicker premature current shut-off. As can be seen in the current experiments (Figure 4A), it is premature current shut-off and not a too weak power output that prevented complete coagulation for an inter-electrode distance of 2.5 and 3 cm.

Should we then lower power and increase treatment duration? In the additional experiments (not shown), lowering power output still allowed complete coagulation for inter-electrode distances up to 2 cm but it took a longer time before current shut-off occurred. Lowering power for an inter-electrode distance above 2 cm indeed prevented current shut-off, but sufficient temperature and complete coagulation were never reached, not even after 20 or 25 min, probably because the electric current density in the centre of the square configuration was too low so that the temperature increase by heat generation could not compensate enough for the temperature decrease by tissue heat conduction (a situation similar to the too weak temperature build up at an inter-electrode distance of 4 cm in Figure 4A).

In other words, at an inter-electrode distance of 2 cm, there is an ideal balance of complete coagulation of the whole volume (especially in the zones furthest away from the electrodes) before current shut-off occurs due to impedance rise (mainly close to the electrodes).

For higher distances, higher power output leads to charring around the electrodes before the whole volume can be treated, while lower power output is too weak to sufficiently heat the increased tissue volume.

The FEM analysis was very helpful to understand the reason and the pattern of incomplete coagulation seen with an increasing inter-electrode distance above 2 cm. RFA heating is quadratically proportional to the electric field (electric potential gradient) (V/m) which is strongest in the area between the positive and the negative electrodes and is weaker when approaching the equator between the two pairs. Up to an inter-electrode distance of 2 cm, the electric field in the square area between the four electrodes is high enough to heat the tissue to 50°C. Above 2 cm, electric current at the equator between the two electrode pairs is too small to generate enough thermal energy.

In the current FEM analysis, electrical and thermal tissue conductivity were considered as constant. In reality, electrical [19], [30], [31] and thermal [32–34] conductivity are temperature dependent. We are working on enabling RAFEM to handle this temperature dependency to improve accuracy.

We have used the 50°C isotherm to predict the ablation zone by FEM analysis, similar to nearly all authors performing FEM analysis of RFA in the liver [23–27]. In the current study, the 50°C isotherm was found to overestimate the experimentally observed coagulation diameter by about 5 mm (Table II). Confronted with this overestimation, we have looked more carefully at the literature and have found that the 50°C isotherm for ablation of liver tissue has not been firmly validated and is used more as a matter of tradition.

Only two authors have compared isotherms with actual ablation zones in the liver [31], [35]. In FEM analysis of RFA in ex vivo liver, the actual size of the ablation zone was best predicted by the 60°C isotherm [31]. In patients undergoing MRI-guided RFA for liver tumours, the superiority of the 60°C isotherm over the 55°C and 50°C isotherms was clearly shown in a very recent paper [35].

The use of isotherms to predict irreversible thermal damage, however, needs to be put into perspective. Isotherms may wrongly suggest that tissue remains viable under this threshold temperature and inevitably dies above it. In reality, irreversible thermal damage depends both on temperature and exposition time. The higher the temperature, the shorter the time needed to induce irreversible cell damage and vice versa. In other words, thermal damage does not depend as much on a single end temperature value but on the whole temperature history, i.e. the evolution of temperature at every moment of the ablation process [36].

Nevertheless, although imperfect, the current FEM analysis calculating electric fields and isotherms was found to be very useful to better understand the ‘pathogenesis’ of RF ablation zones. FEM analysis therefore may be helpful in the development and improvement of more complex RFA electrodes and ablation protocols.

We do not see this four-electrode array as a device which is ready to be used in patients. The size of the reliable ablation zone (3 × 2 × 2 cm) in the current experiments is still too small to be useful in the clinical setting. Moreover, the ablation zone is rectangular while most tumours to be ablated are more or less spherical. Rather we see this array as a platform to gain more insight and to optimise the application of RFA by means of four simple needle electrodes. These 2 × 2 parallel electrodes can then be seen as the elementary building unit of a set of x times y parallel electrodes of different lengths in a rectangular grid. It is hoped that such a set of x times y parallel electrodes of different lengths will enable the creation of a reliable ablation zone of any predefined size or shape, since the total ablation zone will be the sum of the rectangular ablation zones between each of the many four-electrode subunits of such a multiple electrode set.

Conclusion

In summary, we developed a bipolar four-electrode system with simple needle electrodes with a 3-cm active tip and determined the optimal inter-electrode distance. At the optimal inter-electrode distance of 2 cm the coagulation zone was obtained in a short time, very predictable in size and shape and always complete without voids.

The experimental set-up may serve as a platform to gain more insight and to optimise the application of RFA by means of 4 or more simple needle electrodes.

Acknowledgements

The authors wish to thank Marie-Bernadette Jacqmain and Christian Deneffe for the illustrations.

Declaration of interest: This work was partially supported by the grants awarded by the KU Leuven Molecular Small Animal Imaging Centre MoSAIC (KUL EF/05/08); the centre of excellence In vivo Molecular Imaging Research (IMIR) of KU Leuven; and a European Union project Asia-Link CfP 2006-EuropeAid/123738/C/ACT/Multi-Proposal No. 128-498/111. Yicheng Ni is currently a Bayer Lecture Chair holder. The authors alone are responsible for the content and writing of the paper.