Feasibility study of an internally cooled bipolar applicator for RF coagulation of hepatic tissue: Experimental and computational study

Abstract

Purpose: To study the capacity of an internally cooled radiofrequency (RF) bipolar applicator to create sufficiently deep thermal lesions in hepatic tissue.

Materials and methods: Three complementary methodologies were employed to check the electrical and thermal behaviour of the applicator under test. The experimental studies were based on excised bovine (ex vivo study) and porcine liver (in vivo study) and the theoretical models were solved by means of the finite element method (FEM).

Results: Experimental and computational results showed good agreement in terms of impedance progress and lesion depth (4 and 4.5 mm respectively for ex vivo conditions, and ≈7 and 9 mm respectively for in vivo conditions), although the lesion widths were overestimated by the computer simulations. This could have been due to the method used to assess the thermal lesions; the experimental lesions were assessed by the white coagulation zone, whereas the tissue damage function was used to assess the computational lesions.

Conclusions: The experimental results suggest that this applicator could create in vivo lesions to a depth of around 7 mm. It was also observed that the thermal lesion is mainly confined to the area between both electrodes, which would allow lesion width to be controlled by selecting a specific applicator design. The comparison between the experimental and computational results suggests that the theoretical model could be usefully applied in further studies of the performance of this device.

• experimental model
• finite element method
• hepatic resection
• internally cooled bipolar electrode
• radiofrequency ablation

Introduction

Radiofrequency (RF) energy devices are widely used to thermally coagulate hepatic tissue, e.g. in the destruction of surface tumours [1], [2] or minimising blood loss during hepatic resection by creating thermal coagulative necrosis along the transection plane [3]. In both cases the goal is to achieve sufficiently deep thermal lesions. In the former case the lesion should be deep enough to completely destroy the tumour, while in the latter the objective is to seal the small vessels in the transection zone [4].

RF energy is applied to the tissue mostly by a monopolar arrangement between an active electrode and a large conductive patch (dispersive electrode) in contact with the patient's skin. The TissueLink dissecting sealer (Medtronic, Portsmouth, NH, USA) is one of the most widely used electro-surgical devices in hepatic coagulation. Briefly, it is a monopolar electrode cooled by flushing saline through openings in the electrode. This cooling method was previously proposed for RF cardiac ablation in order to obtain deeper lesions and prevent both excessive heating at the electrode–tissue interface and thrombus formation on the electrode [5–7]. In hepatic RF coagulation this cooling method (also known as saline-linked) was used to prevent surface charring and keep tissue surface temperature below 100°C [1]. However, this does not prevent the temperatures in the subsurface from rising above 100°C, which can lead to steam formation and expansion and even to disruption of the surface. The steam may be audible as ‘steam pops’. In fact, undesirable effects such as steam pops, impedance rise and charring of the tissue surface (and in some cases disruption) have been observed in RF heating of cardiac and hepatic tissue [1], [5], [6] with both open and closed irrigation [5], [6]. The use of closed irrigation (or internally cooled) RF electrodes has been proposed not only for RF cardiac ablation [8] but also for RF-assisted resection of liver, kidney and pancreas [9–11] to minimise blood loss during resection.

Saline-linked technology has recently been implemented in a bipolar arrangement in the Aquamantys System (Medtronic) [12]. In general, bipolar electrodes are composed of two identical electrodes between which RF current flows. This arrangement requires less power than the monopolar configuration to achieve the same coagulating effect and has the additional advantage of not needing a dispersive electrode, thus avoiding the risk of skin burns by poor contact between the skin and the dispersive electrode. But most importantly, the use of bipolar electrodes prevents RF currents flowing through adjacent tissue, thus minimising the risk of injury to other organs. This is especially important when surgery is performed by the laparoscopic approach in conditions of reduced visibility [13].

Devices based on saline drip, such as open irrigation RF electrodes, have certain disadvantages when compared to closed irrigation electrodes: (1) the risk of burning contiguous organs by hot saline, and (2) the saline flow rate is critical for producing the desired haemostatic effect without excessive charring [14]. An internally cooled bipolar RF applicator would therefore combine the above-mentioned advantages of the bipolar configuration and would not have the drawbacks associated with open-irrigation RF electrodes. Although some designs have been proposed for internally cooled bipolar RF applicators, such as the Isolator (Atricure, Cincinnati, OH USA), designed to create thermal lesions in cardiac tissue to cure atrial fibrillation [15], these electrodes had not previously been considered to coagulate hepatic tissue, in particular to create thermal lesions sufficiently deep for surface RF ablation or as sealing devices during surgical resection. We therefore conducted a feasibility study of a closed irrigation bipolar RF applicator. The study was based on three complementary methodologies: ex vivo, in vivo and theoretical models. Due to their low cost, the ex vivo and theoretical models were used in the first step to check the electrical and thermal performance of the applicator under test. When its ability to create deep lesions had been assessed we then conducted a pilot experimental in vivo test to check the results in a pre-clinical scenario. Finally, additional computer simulations that modelled the in vivo scenario were conducted to study the effect of the applied voltage and duration on the lesion depth and to determine the potential of the cooled bipolar applicator to coagulate hepatic tissue. These simulations were extended to the case of a smaller applicator especially designed for laparoscopic use.

Materials and methods

Description of the device

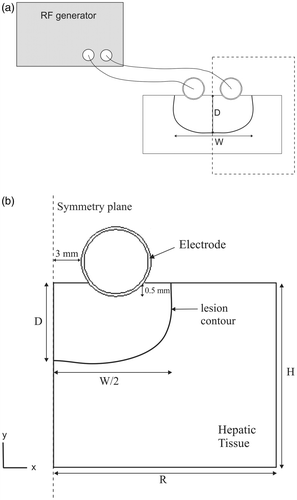
Figure 1 shows the proposed device (D1), which consists of two identical electrodes 5 mm in diameter and 25 mm long, separated by a distance of 6 mm. We chose long rather than pointed electrodes (as in the Aquamantys System) since we needed an applicator able to create thermal coagulative necrosis along the transection plane, as achieved by systems based on multiple electrode arrays [16]. Internal cooling was set at a volumetric flow rate of 100 mL/min and a coolant temperature of 5°C. The electrodes were connected to a CC-1 Cosman Coagulation System RF generator (Radionics, Burlington, MA, USA), which delivers a non-modulated sinusoidal waveform up to 100 V (rms) to a 100 Ω load at a maximum current of 1 A.

Figure 1. Top (a) and side (b) views of the internally cooled bipolar applicator proposed to coagulate hepatic tissue.

Ex vivo experimental set-up

Six lesions were performed on the surface of excised bovine liver (4.5 kg weight, 17°C initial temperature). The collagenous capsule (Glisson's capsule) covering the external surface of the liver was removed prior to the RF application. Room temperature was 22°C. Internal cooling was conducted by means of a Watson-Marlow model 323 peristaltic pump (Wilmington, MA). We analysed impedance progress during RF heating and the geometry of the lesions created in the tissue after each heat application. Impedance was sampled at 30 Hz and processed by means of Agilent VEE software (Santa Clara, CA, USA). Each lesion was sliced transversally in order to characterise its geometry. The thermal lesion geometry was assessed by the white coagulation zone and its depth (D) and maximum width (W) were quantified. Both parameters were expressed as the mean ± standard deviation. A Mann-Whitney test was used to analyse the differences between groups. Data collection and analysis of impedance progress were performed with Matlab® (MathWorks, Natick, MA) and SPSS 17.0 (Chicago, IL, USA), respectively.

In vivo experimental set-up

An in vivo pilot study was performed on a Landrace pig (58 kg) obtained from the farm of the Universitat Autònoma de Barcelona, Spain, with the authorisation of the Ethical Commission of Animal and Human Experimentation (Spanish Government) and under the control of the Ethical Commission of the Universitat Autònoma de Barcelona (Authorisation Number CEAAH 1256). The anaesthesia was supervised by a fully trained veterinary staff member. A combination of azaperone and ketamine (4 mg/kg intramuscularly (i.m.) and 10 mg/kg i.m.) was used for initial sedation. Once sedated, intravenous access was obtained by placing a 20-gauge catheter in a marginal ear vein and morphine (0.2 mg/kg i.m.) and meloxicam 0.2 mg/kg intravenously (i.v.)) were given as analgesic therapy. Anaesthetic induction was performed with propofol (4 mg/kg i.v.) and maintained with isofluorane (vaporiser setting 2%) and 100% oxygen through a semi-closed circular system (25 mL/kg/min oxygen). Lactated Ringer's solution (10 mL/kg/h) was administered through the same catheter throughout surgery. Ventilation was controlled using intermittent positive pressure ventilation (SAV 2500 ventilator, B. Braun, Barcelona, Spain) in order to maintain normocapnia. During the surgical process, temperature, heart rate, respiratory frequency, expired CO₂, arterial pressure, pulse, and electrocardiography were monitored by a Datex Ohmeda Cardiocap II monitor (GE Healthcare, Chalfont St Giles, UK). The animal was aseptically prepared for surgery and a cranial laparotomy was performed to access the liver. The four hepatic lobes were exposed and ten RF coagulations were conducted on the liver surface (35°C) using a constant voltage of 50 V (rms) for 60 s. Room temperature was 20°C. Internal cooling was conducted by means of a PE-PM Radionics peristaltic pump (Integra Radionics, Burlington, MA). Impedance progress was registered during RF heating for each lesion. The pig was euthanised after the study by an i.v. dose of sodium pentobarbital. As in the ex vivo study, liver excision was performed post-mortem in order to assess the lesions.

Theoretical modelling

Theoretical models were based on a coupled electro-thermal problem, which was solved numerically using the finite element method (FEM) with COMSOL Multiphysics software (Burlington, MA). The governing equation for the thermal problem was the bioheat equation [17]:where T is temperature, t is time, k is thermal conductivity, ρ is density and c is specific heat. The term Q_m is metabolic heat generation and is ignored in the RF of the liver, since it has been shown to be insignificant; and Q_p is heat loss from blood perfusion:where ρ_b is the density of blood (1000 kg/m³) [18], c_b is the heat capacity of blood (4,180 J/kg·K) [18], T_b is the blood temperature (37°C), and ω_b is the blood perfusion coefficient. The term Q_p was only considered in the simulations of the in vivo conditions. For this case, a blood perfusion coefficient of (corresponding to a 60% perfusion level) was considered [18]. The term Q_p was discarded when modelling ex vivo situations. Term q is the heat source from RF power (Joule loss) which is given by where |E| is the magnitude of the vector electric field (V/m) and σ is the electrical conductivity (S/m). The value of this vector is calculated from where Φ is the voltage (V). The voltage is obtained by solving Laplace's equation, which is the governing equation of the electrical problem:

At the RF frequencies (≈500 kHz) used in RF heating and over the distance of interest (electrical power is deposited within a small radius around the electrode) the biological medium can be considered almost totally resistive, since the displacement currents are much less important than conduction currents. A quasi-static approach is therefore possible to solve the electrical problem [19].

Tissue vaporisation was modelled by using the enthalpy method [20], [21]. This was performed by modifying Equation 1 and incorporating the phase change according to [22], [23]:where h was the enthalpy. For biological tissues, the enthalpy is related to the tissue temperature by the following [20], [24]:where ρ_i and c_i were tissue density and specific heat of liquid tissue (i = l) and the post-phase-change tissue (i = g), respectively; h_fg was the latent heat and C the tissue water content. We considered a value of latent heat of 2.162·10⁹J/m³, which corresponds to the product of the water vaporisation latent heat and the water density at 100°C, and a tissue water content of 0.68 inside the liver tissue [25].

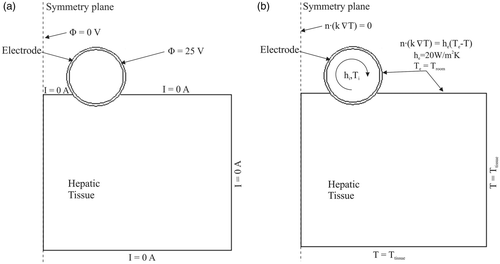
Figure 2 shows the physical situation modelled and the proposed theoretical model, which represents the device over a fragment of hepatic tissue. Since there is a symmetrical plane, the model only includes half of the electrode–tissue set. The electrode, which has the same diameter as the device used in the experiments (Figure 1), was assumed to be inserted in the tissue to a depth of 0.5 mm and was separated from the symmetrical plane by 3 mm (6 mm inter-electrode distance).

Figure 2. (a) Physical situation considered in the study. The dashed rectangle indicates the region considered in the theoretical model. (b) Theoretical model proposed (out of scale). R and H: dimensions of the hepatic tissue. The inner and outer electrode diameters are 4.5 and 5 mm, respectively. Since there is a symmetrical plane, the model only includes half of the electrode–tissue set. Lesion depth (D) and width (W) were assessed by an Arrhenius damage model (see text for more details).

Tissue dimensions R and H were estimated by means of a convergence test in order to avoid boundary effects, using as control parameter the value of the maximal temperature achieved in the tissue (T_max) after 60 s of heating. We first considered a tentative spatial (i.e. minimum meshing size) and temporal resolution. To determine the appropriate values of R and H we conducted a computer analysis by increasing the value of these parameters by equal amounts. When the difference between T_max and the same parameter in the previous simulation was less than 0.5%, we considered the former values of R and H to be adequate. We then determined adequate spatial and temporal resolution by means of other convergence tests using the same control parameter as in the previous test. Discretisation was spatially heterogeneous: the finest zone was always the electrode–tissue interface, since it is known that this has the largest voltage gradient and hence the maximum value of current density. In the tissue, grid size was increased gradually with distance from the electrode–tissue interface. The optimum spatial discretisation was achieved by refining the mesh in this zone so that T_max was within 0.5% of the value obtained from the previous refinement step. With an adequate spatial resolution achieved, we decreased the time step until T_max was within 0.5% of the value obtained from the previous time step.

The thermal and electrical characteristics of the model elements (electrode and tissue) are shown in Table I [25–27]. The electrical and thermal conductivity were temperature-dependent functions. For electrical conductivity we considered an exponential growth of +1.3%/°C and + 1.7%/°C up to 100°C for the ex vivo and in vivo model, respectively. These values were chosen since they provided the best fit for the impedance progress (initial decreasing slope) of the experimental and computational results. Between 100° and 105°C, σ was kept constant and then decreased linearly by two orders for five degrees [21]. Thermal conductivity grew linearly +1.5%/°C up to 100°C, and from then on was kept constant [17].

Table I.  Thermal and electrical characteristics of the elements employed in the theoretical modelling (data from Pätz et al., Berjano et al. and Duck [25–27]): σ, electric conductivity; k, thermal conductivity; ρ, density; and c, specific heat.

Element/material	σ (S/m)	k (W/m·K)	ρ (kg/m^3)	c (J/kg·K)
Electrode	7.4·10^6	15	8000	480
Liver	σo*	0.502**
Liquid phase			1080	3455
Gas phase			370	2156

*σ_o:assessed at 17°C and adjusted to achieve the same initial impedance as in the experiments: 0.37 and 0.71 S/m for ex vivo and in vivo, respectively; **assessed at 37°C.

Figure 3 shows the electrical and thermal boundary conditions. For the electrical boundary conditions (Figure 3a), a constant voltage of 25 V was applied to the electrode and 0 V on the symmetry plane, which was equivalent to 50 V (rms) in the experimental set-up. A null electrical current was assumed on surfaces at a distance from the electrode and on the tissue-ambient and electrode-ambient. Impedance value was calculated from the ratio of applied voltage to total current, which was calculated as the integral of the current density (A/m²) over the symmetry plane, where current density is

Figure 3. Electrical (a) and thermal (b) boundary conditions of the theoretical model.

For the thermal boundary conditions (see Figure 3b), a null thermal flux was used on the symmetry plane. The temperature on surfaces at a distance from the electrode (T_tissue) was 17°C and 35°C for modelling the ex vivo and in vivo situations, respectively. The effect of free convection at the tissue-ambient and electrode-ambient interfaces was taken into account using a thermal transfer coefficient (h_e) of 20 W/m²K. Room temperature (T_e) was 22°C and 20°C, respectively, for modelling the ex vivo and in vivo situations. The thermal boundary condition of convective coefficient (h_i) was applied to the inner electrode in order to model the cooling effect of the circulating fluid. The value of h_i for laminar flow [28] was calculated using:where Nu is the (dimensionless) Nusselt number, k_f is the thermal conductivity of circulating fluid (W/m·K), L is the length of the heated area (parallel to the direction of the flow), which was fixed at 25 mm (length of electrode in contact with the tissue, see Figure 1B). The average Nusselt () can be estimated from Equation 7:where Re is the Reynolds number and Pr is the Prandtl number (both dimensionless). Equation 7 is valid for Re < 5·10⁵. These numbers are calculated from Equations 8 and 9:where ρ_f is the density of circulating fluid (kg/m³), μ is the dynamic viscosity (N·s/m), c_f is the specific heat at constant pressure (J/kg·K) and u is the velocity of the flow (m/s) calculated as:where F is the flow rate of the circulating fluid and A_t is the cross-sectional area of the tube = π·(0.0025)²= 1.9635·10⁻⁵·m². We obtained a value for h_i of 1537 W/m²·K (flow rate of 100 mL/min). The characteristics of the circulating fluid were considered to be those of water at 37°C: k_f = 0.63 W/m·K, ρ_f = 999.4 kg/m³, μ = 6.9·10⁻⁴ N·s/m, y c_f = 4174 J/kg·K. We considered a coolant temperature of 5°C.

In each simulation we obtained the impedance progress for 60 s of RF heating and the lesion zone dimensions created in the tissue. These variables were used to compare the computational and experimental results. In order to conduct this comparison we adjusted the initial impedance of the tissue in the theoretical model to the mean value obtained in each experimental study. This was done by varying the initial tissue electrical conductivity (σ_o) to achieve the same initial impedance as in the experiments (see Table I).

The lesions were assessed by the Arrhenius damage model [29], [30], which associates temperature with exposure time using a first order kinetics relationship:where Ω(t) is the degree of tissue injury, R is the universal gas constant, A is a frequency factor (s⁻¹), and ΔE is the activation energy for the irreversible damage reaction (J/mol). The parameters A and ΔE are dependent on tissue type; for the liver we considered those proposed by Jacques et al. [31]: A = 7.39·10³⁹·s⁻¹ and ΔE = 2.577·10⁵ J/mol. We employed the thermal damage contour Ω = 1 which corresponds to a 63% probability of cell death. The change in the perfusion term with temperature was taken into account when modelling the in vivo condition. We considered the cessation in tissue perfusion (Q_p = 0) for Ω > 1 (under which tissue coagulation is assumed to occur) [29].

Finally, after comparing the thermal lesions computed from the theoretical models with the experimental values, we conducted an additional set of simulations using the theoretical model of the in vivo conditions and varying the applied voltage and duration values. The aim here was to explore the effect of these parameters on lesion dimensions from a computational point of view. We also repeated these simulations by considering a small applicator (D2) with 3 mm diameter electrodes separated by a distance of 4 mm, which would allow it to be passed through a trocar in laparoscopic surgery.

Results

After the convergence tests conducted with the theoretical models, we obtained a value of R = H = 50 mm (tissue dimensions), a grid size of 0.115 mm in the finest zone (electrode–tissue interface), and a step time of 0.05 s. The theoretical model had nearly 2,500 triangular elements. Figure 4b shows the side views of the thermal lesions created experimentally for the ex vivo and in vivo conditions. Figure 4c shows temperature distributions from the computer simulations for the ex vivo and in vivo conditions. As expected, the lesions are mainly limited to the area between the electrodes, especially on the surface tissue. This is especially noticeable in Figure 4a, where the surface view of a lesion (ex vivo) shows a very limited contour along the entire length of the electrodes.

Figure 4. Thermal lesions created after 60 s of RF heating at 50 V (rms), considering a flow rate of 100 mL/min and a coolant temperature of 5°C. (a) Surface view of lesion created in the ex vivo model, (b) side views of lesions created in the ex vivo (top) and in vivo (bottom) models. (c) Temperature distributions from computer simulations of the ex vivo (top) and in vivo (bottom) conditions (scale in °C). The lesions were characterised by the depth (d) and maximum width (W) parameters. Experimental lesions were assessed by the white coagulation zone contour and in the computer simulations by an Arrhenius damage model (the solid black contour corresponds to Ω = 1).

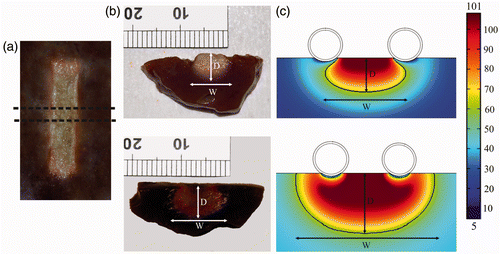
Table II shows the lesion dimensions for both ex vivo and in vivo experimental conditions and the values estimated from the computer simulations in the corresponding conditions. In general, the theoretical model tended to overestimate lesion width by 45% in the ex vivo case and up to 100% in the in vivo case. In contrast, the computational estimation of the lesion depth was more accurate in both cases, by around 13% ex vivo and 45% in vivo.

Table II.  Lesions dimensions created by the internally cooled bipolar applicator under ex vivo and in vivo experimental conditions together with the values estimated from computer simulations for the same conditions.

Condition	Methodology	Depth (mm)	Width (mm)
Ex vivo	Computational	4.54	11.19
	Experimental (n = 6)	4.03 ± 0.14	7.67 ± 0.41
In vivo	Computational	9.62	22.20
	Experimental(n = 10)	6.85 ± 1.25	10.90 ± 1.22

In the ex vivo case a strong correlation was found between the initial impedance of the hepatic tissue and the lesion dimensions: R²= 66% for depth and 77% for width, but this correlation was found to be very weak (<15%) in the in vivo case.

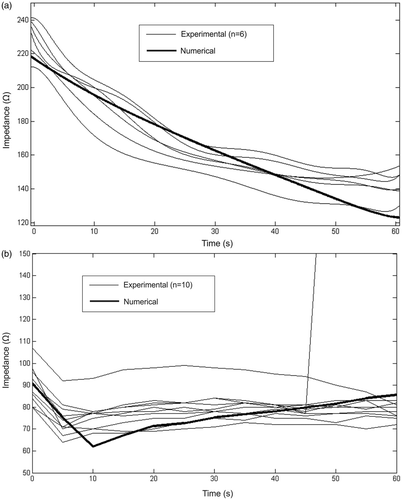
Figure 5 shows impedance progresses during RF heating in the ex vivo (Figure 5a) and in vivo study (Figure 5b). The initial impedance was different in both cases (231.13 ± 9.60 Ω and 90.10 ± 8.56 Ω respectively) and progress was also slightly different. Ex vivo impedance progressively decreased during the entire period while in vivo impedance fell rapidly in the first 10 s and then increased at a slower rate until the end point. In one case of the in vivo set-up there was an abrupt impedance rise (roll-off) at 45 s. Figure 5 also shows the impedance progress obtained from the theoretical models (solid lines), which shows that in general there is good agreement between the computational and experimental results.

Figure 5. Impedance progresses during RF heating in the ex vivo (a) and in vivo (b) studies. The solid lines show the results of computer simulations of the corresponding conditions. Both cases (ex vivo and in vivo) consider a flow rate of 100 mL/min and a coolant temperature of 5°C. Note that an in vivo experimental case showed an impedance rise (roll-off) at 45 s.

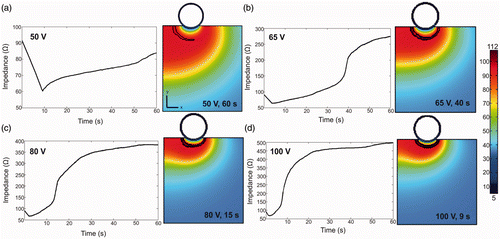
Finally, Figure 6 shows the depth of lesions estimated from the computer simulations of in vivo conditions for the applicator under test (D1) and for the smaller design (D2) when changing the applied voltage (50–100 V) and duration (60–300 s). The results indicate that the heating period has a minimum impact on lesion depth: D1 was seen to increase from 9.62 mm to 17.13 mm and D2 from 9.15 mm to 14.48 mm when the time was increased from 60 s to 300 s. In contrast, when the time was kept at 60 s, the applied voltage did not have a significant influence on lesion depth, which in fact slightly decreased from 9.62 mm to 7.76 mm for D1 and from 9.15 mm to 6.66 mm for D2 when voltage was raised from 50 V to 100 V. The low impact of the applied voltage on lesion dimensions could be due to the fact that increasing the voltage caused a sudden increase of impedance (roll-off), at which time the temperature of the tissue around the electrode reached 100°C. This could have prevented the lesion from going deeper. In this respect, Figure 7 shows the in vivo impedance progresses and tissue temperature distributions computed for the applicator under test by raising the applied voltage from 50 to 100 V. We observed that roll-off occurred at a specific time for each applied voltage and at this time the temperature of the tissue around the electrode was 100°C: 40 s, 15 s and 9 s for a voltage of 65 V, 80 V and 100 V, respectively.

Figure 6. Lesion depths estimated from computer modelling of in vivo conditions for the applicator under test (D1) and the smaller design (D2) when changing applied voltage (between 50 and 100 V) and duration (between 60 and 300 s). D1 and D2 are applicators with 5 and 3 mm diameter electrodes and separated by a distance of 6 and 4 mm, respectively.

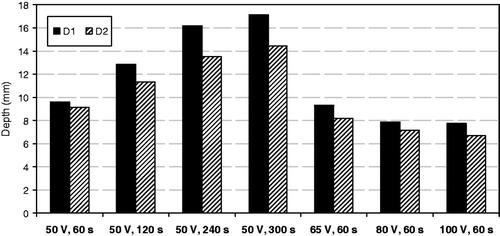
Figure 7. Impedance progresses and tissue temperature distributions computed for in vivo conditions for the applicator under test while changing the voltage (between 50 and 100 V) for a time of 60 s. The contour line corresponds with the 100°C isotherm plotted at the instant at which roll-off occurs. Scale in °C.

Discussion

This study was conducted to assess the capacity of a bipolar cooled RF applicator to coagulate hepatic tissue and especially to quantify the lesion depths created. We used three complementary methodologies: an ex vivo set-up, in vivo experiments and theoretical modelling.

The results of the computer simulations were compared to the experimental results to assess the accuracy of the theoretical models. In general, we observed a tendency in the computer simulations to overestimate the lesion dimensions. However, we also found good agreement between the computational and experimental results of impedance progress, which suggests that the disagreement could have been due to the method used to assess the thermal lesion. The experimental lesions were assessed by the white coagulation zone. Prior to the experimental ex vivo study, we evaluated the relationship between the colour change in liver samples immersed in hot water, water temperature, and immersion time. The samples were heated from 50° to 75°C for times from 15 s to 60 s, as in [32], [33]. We observed that the tissue did not turn white until the water temperature reached 70°C [34]. Since it is known that temperatures around 50°C produce coagulative thermal necrosis, we can state that the experimental lesion dimensions correspond approximately to the boundary of the 70°C isotherm, while the lesion dimensions from the computer simulations using the tissue damage function include a higher amount of tissue at temperatures over 50°C. For this reason the lesions estimated from the theoretical models possibly give a truer representation of the dimensions than the white coagulation contours. Taking the above into account, we consider that the proposed theoretical model would be sufficiently accurate if used to study other issues from a computational point of view.

In practical terms, the experimental results suggest that by using the closed irrigation RF bipolar electrode, it is possible to achieve in vivo lesions with a depth ≈7 mm. If the theoretical model gives a more accurate representation of lesion depth, the value could be around 9 mm. As far as we know, no data have been reported on the lesion depth achieved by the Aquamantys bipolar system, although there are indications that it is typically less than 2 mm [35]. The cooled bipolar applicator tested in this study produces deeper lesions, which could be due to the size of the electrode used (5 mm versus 3.48 mm in the Aquamantys Model 6.0) and the distance between electrodes (6 mm versus 2.53 mm). These dimensional differences would undoubtedly have an influence on the results, as would the different technologies they use: open versus closed irrigation. Previous comparative studies on RF cardiac ablation have not been unanimous in their findings; while some suggest there are no differences between open and closed irrigation at the same power settings [36], others maintain that there are no differences for power levels higher than 20 W [5], [6] but that closed irrigation produces deeper lesions at low power setting (<20 W) [5]. Future studies should be conducted to compare the lesion depths created by both systems in hepatic tissue.

An experimental study on cardiac tissue using the Isolator device based on closed irrigation bipolar RF electrodes reported a mean lesion depth of 5.3 ± 3.0 mm [37]. This shows once again that lesion characteristics are highly dependent on the electrode design (diameter and distance between electrodes), as well as other factors such as contact pressure, power delivering protocol (including power setting), so that a direct comparison with our results is difficult. However, our findings suggest that the applicator studied would be useful for creating sufficiently deep thermal lesions in hepatic tissue to assist in sealing small vessels during surgical resection, or producing a long thermal lesion along the transection plane in preparation for cutting with a cold scalpel.

It should be emphasised that our aim was not to determine the factors affecting the incidence of steam popping or impedance rise (as in Gnerlich et al. [2]), that is, we did not search for the optimum combination of applied voltage and duration. In this respect, the results from additional computer simulations in which these two parameters were varied suggest that lengthening the duration could extend lesion depth to 17 mm. They also suggest that raising the applied voltage will not increase lesion depth. In this regard, we found that at higher voltages the tissue around the electrode reaches ≈100°C and causes an abrupt increase of impedance at a specific time. This interrupts the flow of RF current and consequently limits the size of the lesion. We therefore consider that a value around 50 V would be the optimum.

From a clinical point of view, the applicator tested here is too large to be used in a laparoscopic approach and hence can only be employed in open surgery for both liver resection and surface tumour ablation. However, the theoretical model proposed here could be useful for exploring the suitability of other designs for use with a trocar in laparoscopic surgery. In this respect, the computational results computed for different values of applied voltage and duration were similar to previous results. A lesion depth ≈14 mm could be achieved when the duration is increased. On the other hand, simply raising the applied voltage did not provide deeper lesions.

This study has certain limitations. Firstly, the theoretical model was two-dimensional, while the experimental models were obviously three-dimensional. The comparison between the computational and experimental results suggests that this limitation is not highly significant, at least for the durations used here, since the edge effect observed in the early stages (when heating is mainly confined to the ends of the electrodes) seems negligible for heating times longer than 60 s. Also, the in vivo computer simulations considered only one value for tissue perfusion, although the actual perfusion rate in each lesion zone was unknown under the specific in vivo experimental conditions.

Finally, the differences between the ex vivo and in vivo results could be due not only to the different initial impedance and temperature values, but possibly also to whether or not the Glisson's capsule had been previously removed. The electrical and thermal effect of this layer on lesions should be made the subject of further research. Although its clinical impact seems low, its presence could have caused the steam pops observed in our in vivo study, due to steam accumulating between the hepatic tissue and capsule during heating.

Conclusions

The experimental results suggest that the cooled bipolar RF applicator tested in this study could create lesions with a depth around 7 mm under in vivo conditions and that the thermal lesion is mainly confined to the area between the electrodes, which would make it possible to control lesion width by selecting a specific applicator design. The comparison between the experimental and computational results suggests that the theoretical model could be useful for further studies of the performance of this device.

Declaration of interest

This work received financial support from the Spanish Plan Nacional de I + D + I del Ministerio de Ciencia e Innovación TEC2011-27133-C02-(01 and 02), from Universitat Politècnica de València (INNOVA11-01-5502; and PAID-06-11 Ref. 1988). A. González-Suárez is the recipient of grant VaLi + D (ACIF/2011/194) from the Generalitat Valenciana. The proof-reading of this paper was funded by the Universitat Politècnica de València, Spain. The authors alone are responsible for the content and writing of the paper.