Role of optical coefficients and healthy tissue-sparing characteristics in gold nanorod-assisted thermal therapy

Abstract

Purpose: This study seeks to define parameters for gold nanorod assisted thermal therapy, to achieve the thermal ablation temperature (50–60°C) in the tumour region and spare healthy tissue surrounding the tumour. Also, a criterion for size selection of gold nanorods is described based on the role of optical coefficients.

Theory and methods: In this study a tissue domain (comprising a 3 mm tumour and 7 mm of surrounding healthy tissue) embedded with gold nanorods is irradiated with electromagnetic radiation within the therapeutic wavelength band. Optical interaction is captured using light scattering theory (Mie-electrostatic approach). The resulting temperature field is evaluated using Penne's bioheat model. The effect of key parameters, namely irradiation intensity, irradiation duration and volume fraction, on tissue temperature is also modelled numerically.

Results: With increasing nanorod diameter – from 5 nm to 15 nm – the scattering coefficient increases ∼76 times as compared to a 1.7-fold increase in absorption coefficient. Scattering is considerably minimised by having smaller gold nanorods of 5 nm diameter. For this study, gold nanorods of 5 nm diameter and volume fraction 0.001%, irradiated with 50 W/m²-nm for 250 s ablated the tumour as well as spare healthy tissue 2 mm beyond the tumour region.

Conclusion: Overall it may be concluded that tumour ablation as well as surrounding healthy tissue-sparing (within millimetres immediately adjacent to the tumour) can be achieved through a combination of specified parameters, namely diameter and volume fraction of gold nanorods, irradiation intensity and duration.

• Thermal therapy
• cancer
• nanorods
• irradiation
• optical coefficients

Introduction

Thermal therapy, involving exchange of heat with body tissues, has numerous clinical applications. One especially promising application is hyperthermia or thermal ablation [1], [2]. Hyperthermia can be used alone or in combination with other standard modalities such as radiotherapy and chemotherapy [3], [4]. Tumour regions that are hypoxic may be more poorly perfused, and this can lead to preferential heating. However, tumour cells that are at low pH (not hypoxic) have been shown to be more sensitive to killing by heat [5]. For these treatments, nanotechnology plays an important role [6–8]. Preferential heating of the tumour region can be enhanced by utilising light absorbing nanoparticles [9–11]. Nanoparticles of different material, size and shape have been used for this purpose; examples include gold nanoshells [10], [11], gold nanorods (GNR) [12–14], carbon nanotubes [15], [16] and gold nanocages [17], [18]. Mainly, gold is the material of choice as it is biocompatible [19–21]. Thermal therapy, using light absorbing nanoparticles, is sometimes referred to as ‘plasmonic photothermal therapy’ as it makes use of plasmonic properties of nanoparticles and serves to distinguish it from conventional photothermal therapy (without nanoparticles). Regarding the shape of nanoparticles, many researchers agree that gold nanoshells and nanorods are the most promising because their optical properties are very pronounced over a wavelength range which can be easily tuned. This tuning is possible by modifying the core to shell diameter or aspect ratio in the case of nanoshells and nanorods, respectively. Ideally these nanoparticles are tuned to strongly absorb electromagnetic radiation in the near-IR (600 nm–1300 nm) wavelength range, which is termed the therapeutic band [22]. Towards the middle of this therapeutic band, the healthy tissues do not absorb much radiation; however, absorption get high near the borders of this spectral window. For instance at a wavelength less than 600 nm absorption becomes prominent due to the presence of blood, and similarly at wavelength more than 1300 nm due to the presence of water content in the tissue. It has been reported that gold nanorods exhibit superior spectral bandwidth and photothermal heat generation per gram of gold compared to nanoshells [23].

Considering the importance of nanoparticle-assisted thermal therapy as an evolving tumour-specific therapy [24], [25], there is a need to develop numerical tools to predict the temperature field in and around tumours by modelling the near-IR radiation nanoparticle interaction. This modelling is also important from the viewpoint of pre-treatment planning for such therapy. Also, numerical modelling helps in evaluating and further refining the effect of a wide range of parameters not possible with in vivo trials. There have been attempts towards numerically modelling nanoparticle-assisted thermal therapy in the past [26–29], but the roles of optical coefficients of nanoparticles especially GNR and surrounding healthy tissue-sparing characteristics have not been sufficiently addressed. Most of the work reported is for nanoshells, which have considerable scattering as compared to absorption [30]. In some of the literature [23], the absorption and scattering coefficients have been simply added to evaluate the temperature field, which should not be the case as this will predict temperature differently. Also, in many cases, the spatio-temporal response was calculated in simplified manner such as tumour cells dispersed in a solution [31] without extensive attention to surrounding healthy tissue. Other considerations have not been studied in detail, including volume fraction, shape and size aspects of nanoparticles, irradiation parameters, which are critical in determining the temperature within the tumour as well as surrounding healthy tissue.

In this work the spatio-temporal temperature field within a tumour embedded with gold nanorods surrounded by healthy tissue is evaluated numerically. Apart from describing the role of optical coefficients of gold nanorods, the surrounding healthy tissue-sparing characteristics are investigated for various conditions of irradiation intensity, irradiation duration and volume fraction of gold nanorods. The aim was to specify a set of combined parameters to have GNR-assisted thermal therapy confined to the tumour region and to spare the surrounding healthy tissue.

Theory and methods

A 10 mm thick physical domain representing a tissue, as shown in Figure 1, was considered. The top 3 mm of the domain represented the tumour region (an approximation of melanoma) and the other 7 mm represented surrounding healthy tissue. The tumour region was considered to be embedded with gold nanorods.

Figure 1. Schematic of physical domain representing a surface tumour surrounded by healthy tissue. The top 3 mm of the domain represents the tumour region (an approximation of melanoma) and the other 7 mm represents surrounding healthy tissue. The tumour region is embedded with gold nanorods. The top surface is irradiated with near-IR radiation. Z represents the tissue depth from the surface. (Schematic is not to scale).

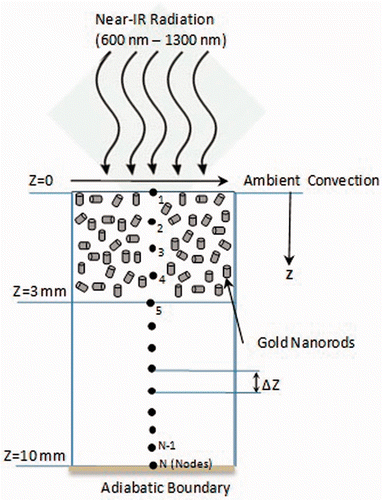
Since one of the prime concerns of this study is to highlight the role of optical coefficients, it was assumed that the nanorods were uniformly distributed in the tumour region. Distribution of nanoparticles was governed by the delivery route – i.e. intramuscular [32–34] or intravenous [35], [36]. It is believed that GNR volume fraction is one of the main parameters that governs the extent of radiant energy penetration in the tissue. This is because a higher volume fraction leads to higher absorption of incident intensity by GNR near the top surface. Alternatively, a lower volume fraction may not give sufficient overall temperature rise in the tissue domain. Therefore a GNR volume fraction range of 0.0002% to 0.005% was considered representing a considerable low dose. The electromagnetic radiation source was assumed to have a spectral intensity of 50–100 W/m²-nm with a flat profile in the therapeutic band. Addition of the ‘nm’ units to the intensity represents spectral dependence of optical coefficients, and for a broadband source the spectral intensity was to be integrated over the wavelength band. For typical plasmonic spectral width (650–900 nm) of a 5-nm GNR, the integrated intensity came out to be 1.25 W/cm². This value is in line with those used by researchers considering single wavelength sources − 0.75–2 W/cm² and 4 W/cm² [10], [23]. Optical coefficients of gold nanorods were calculated using the theory of light scattering by small particles (MIE electrostatic approach). Through careful selection of GNR diameter and aspect ratio, the scattering was minimised as depicted by absorption efficiencies relative to scattering in the results section. Penne's bioheat model, discretised using the finite difference method, was used to evaluate the temperature distribution considering temperature dependent blood perfusion. It has been reported that a temperature of approximately 50°C maintained for over 4–6 min results in tissue damage through protein denaturisation, cellular coagulation and necrosis [37]. At the same time it has been observed that most of the tissues can tolerate temperatures up to 44°C for 1 h duration without significant damage [1]. In light of these observations, volume fraction of GNR, irradiation intensity and duration were chosen to maintain ablation temperature of ≥50°C for a certain time in the tumour region while maintaining the surrounding healthy tissue below 44°C.

Optical coefficients of GNR embedded tissue

A theory for the interaction of radiation with nano-sized particles was first developed by G. Mie in 1908. Near-IR radiation interaction and thus optical coefficients of nanoparticles are highly dependent on the incident radiation wavelength. Other factors which determine the optical coefficients are material (dielectric function), size (diameter, aspect ratio) and shape of nanoparticle. Consider a nanoparticle of diameter D, having bulk dielectric function , placed in a medium having dielectric function and irradiated with near-IR radiation. For ( being wavelength of incident radiation), the nanoparticle experiences a spatially uniform electric field and behaves as a dipole with induced oscillations [38]. This is referred to as the electrostatic approach, and is being used by many researchers to explain and correlate the measured absorption spectra of nanoparticles of different sizes and shapes [39–41]. This approach predicts accurate optical coefficients for nanoparticles of diameter less than 100 nm, irradiated with near-IR radiation [40]. Nanorods are typically cylindrical shaped particles having diameter D and length l. In the case of nanorods with dielectric function , embedded in a medium of dielectric function , the polarisation (α_i) is given by Equation 1.where i = 1, 2, 3 represents the number of axes. The geometric factor (P_i) is given by Equation 2.where

For a medium embedded with volume fraction fv of nanorods, the scattering and absorption coefficients are given by Equations 3 a and 3b respectively.where, V_np is the volume of a nanorod and λ is the wavelength of the incident radiation. In Equation 3b imag denotes the imaginary part. In the case of metallic particles, oscillations of the free electrons are responsible for their optical properties. Nanorods experience oscillations of electrons along the radial as well as axial direction, resulting in two plasmon peaks corresponding to transverse and longitudinal oscillations. It is well known that dielectric function of a bulk material is frequency dependent. At the nanoscale, as size approaches mean free path of electrons (42 nm for gold and 50 nm for silver), the dielectric function is also influenced by the size of nanoparticle as well as frequency [41]. So the oscillations of the conduction electrons are restricted due to damping. There are few models which takes this aspect into account to evaluate the dielectric function – namely Drude's model and Kreibig-Vollmer model, but Drude's model does not account for the intra-band transitions [39]. So Equation 4 given by Kreibig-Vollmer was considered to incorporate size and frequency dependence of dielectric function in the present model.where and . In Equation 4, ω is the angular frequency of incident light and ω_p is the plasmon frequency of free electrons. The symbols n_o and denote the number density of electrons and permittivity of vacuum, respectively. The symbols m_e and e denote the mass and charge of the electron, denotes the damping coefficient arising due to size of nanorod. is the free damping coefficient due to electron–electron, electron–phonon and electron–defect scattering. is defined as the ratio of Fermi velocity v_F and mean free path of the electrons. A is proportionality constant based on experimental data and is generally taken as 1. The meanings and values of other standard symbols are mentioned in Table I. Dielectric function data of bulk gold were taken from the literature [42].

Table I.  Thermophysical properties and constants.

Property	Value	Property	Value
Density of tissue, ρt	1200 kg/m^3	Free electron density, no	5.9 × 10^28 /m^3
Specific heat of tissue, Ct	3300 J/kgK	Permittivity of vacuum, εo	8.85 × 10^−12F/m
Blood perfusion, wb	1.41 × 10^−3m^3s^−1m^−3	Refractive index of air, n1	1.0003
Density of blood, ρb	1060 kg/m^3	Refractive index of tissue, n2	1.45
Metabolic heat, qm	1091 W/m^3	Charge on electron, e	1.6 × 10^−19C
Specific heat of blood, Cb	3770 J/kgK	Mass of electron, me	9.1 × 10^−31kg
Thermal conductivity of tissue, Kt	0.45 W/mK	Fermi velocity, vF	1.39 × 10^6m/s

Spatio-temporal temperature field in the GNR embedded tissue

Generally, when a bare tissue (without embedded GNR) is exposed to electromagnetic radiation which lies within the therapeutic band, negligible energy absorption takes place in the tissue [43]. The numerical calculations of GNR optical coefficients consider the tissue as background medium through its refractive index. For a tissue (without embedded GNR), the absorption and scattering values are typically 0.062 1/mm @725–925 nm and 0.95 1/mm @935 nm respectively [44]. Whereas, for the GNR (5 nm diameter and aspect ratio 3) embedded tissue, the computed peak absorption and scattering values are 10 1/mm and 0.037 1/mm respectively. So, for a tissue without GNR, the absorption is negligible for the irradiance level considered in the study. The addition of nanorods significantly modifies the optical characteristics of the tissue. A GNR embedded tissue acts as a strongly absorption-dominated medium (as GNR scattering is minimised through proper selection of size as shown in the results section) in contrast to bare tissue. In a strongly absorption-dominated media , the incident radiation gets absorbed before its propagation is significantly affected by a scattering event [45] and thus intensity attenuation can be evaluated using Equation 5.

In Equation 5, represents the intensity of incident radiation and is the intensity attenuated through each layer of thickness ΔZ, the direction Z has been shown in Figure 1. The fraction of energy reflected (R) at the air–tissue interface was evaluated as per Fresnel's formula given in Equation 5 a. The symbols n₁ and n₂ denote the refractive index of air and tissue respectively. Heating of the tissue is caused by the absorbed intensity and not by the scattered intensity. For every pass through the nodal layer, scattering (though negligible) was considered for intensity attenuation, but only absorption was counted for heat generation. Also, the path length or thickness of each nodal layer was kept less than the average scattering distance – a condition for the application of Equation 5 [46]. Also, for the considered GNR diameter and irradiance, the scattering does not modify the heating characteristics.

Once the radiant energy absorption was known, the spatio-temporal temperature field within the tissue domain was evaluated using Penne's bioheat model. Penne's model is a fundamental, versatile, well accepted model considering overall blood perfusion [47]. In Penne's model, blood flow in tissue capillaries is assumed to be isotropic, neglecting local vascular geometry and blood flow directionality. Blood enters capillary beds at core body temperature and comes to equilibrium with local tissue temperature. Equation 6 represents Penne's bioheat model.

In Equation 6, T and T_c represent the temperature of tissue and core body (37°C) respectively. The meanings and values of other symbols used in Equation 6 are mentioned in Table I.

On the right hand side of Equation 6, the first term accounts for spatial variation of temperature. The second term represents the contribution of blood perfusion towards temperature. The third term represents the metabolic heat generation rate and symbol q_a denotes the amount of heat gained due to irradiation. As the human body is a thermoregulatory system, an increase in blood perfusion rate (w_b) has been observed during thermal therapy. Considering this, the blood perfusion rate was varied in the model based on experimental data [48]. An equation was obtained by curve fitting the data over a temperature range of 37°C to 45°C, giving the perfusion rate, [49]. Also, when tissue suffers permanent damage, its vasculature gets damaged and blood perfusion generally stops at this stage [50]. So the temperature field results were obtained by considering an increasing blood perfusion rate until the tissue temperature of 45°C, and setting the blood profusion rate to zero at higher temperatures. This case of perfusion is termed ‘restricted perfusion’ for illustration in the results and discussion section. Penne's equation was discretised using the forward difference implicit method and its discretised form is shown in Equation 7.

In Equation 7, Δt and ΔZ denote time step and spatial step respectively. The superscript p and m represent instantaneous time step and node number respectively. The dielectric function and geometric factor of GNR, obtained using Equations 2 and 4, were input into Equation 1. Then the optical coefficients of GNR were computed using Equation 3. Once the optical coefficients were found, the incident energy absorbed by GNR in each nodal layer was computed using Equation 5 and input into Equation 7 through the parameter q_a. The discretised nodal equations were then solved through the matrix inversion method given in [51].

The top surface boundary was subjected to the ambient natural convection condition of 5 W/m²K at 25°C. An adiabatic boundary condition was assumed at the bottom surface of the domain considering that skin tissue has a hypodermal layer below it, which contains fat and acts as a thermal insulation for deeper tissue. The tissue was initially assumed to be at a uniform core body temperature of 37°C. Incident radiation was divided into interval bands of 10 nm to accurately capture the plasmon response. The model domain was divided into uniform nodal regions with ΔZ  =  100 μm and time step was taken as Δt  =  45 ms. Each discretised interval was chosen such that the iterations consistently gave convergent, stable and grid independent results.

After choosing a specific diameter of GNR, the effect of irradiation intensity, irradiation duration and GNR volume fraction on the temperature field were also simulated. The healthy tissue-sparing characteristics, through careful selection of the above parameters, were also interpreted from the results of the developed numerical model.

Validation of the numerical model

The developed model is validated by comparing the predicted results (after reducing the developed model to a single wavelength-based interaction and incorporating the experimental study parameters) with two published experimental studies [10], [23]. The predicted peak plasmon wavelength of GNR very well matches with the reported experimental values, whereas the predicted full spectral width at half maximum is a bit narrower than the reported experimental value, due to the mix (inevitable variation in size and shape) of GNR sampled in the experimental study [23]. This is referred to as the broadening of the plasmon band. The developed model incorporates wavelength-dependent interaction to efficiently utilise this absorption over a broad wavelength range. The predictions for the surface temperature (at the end of 5 min) are slightly higher (6–8°C). This is due to the difference of non-uniform GNR distribution in the tumour due to intravenous injection [23]. Also, the reported initial steep rise in the temperature is due to accumulation of GNR in that region. Apart from the laser intensity and duration, the GNR size as well as volume fraction plays a critical role as explained by the results of this numerical study. Also, in this study the temperature–time results are presented until tissue cool down, which gives a clear picture of thermal damage unlike considering the heating cycle only and not recording the temperatures further down the time. This combination of parameters is what has been described in the current study to achieve desired surrounding healthy tissue-sparing characteristics – which unfortunately were not recorded in the experimental study [23]. Towards healthy tissue-sparing characteristics, the trends of predicted temperature–time plots at various tissue depths were compared and are in good agreement with those measured (through MRI) by the experimental study mentioned in reference [10].

Results and discussion

Role of optical coefficients

To begin with, the effect of parameters such as aspect ratio and GNR size on the optical coefficients were investigated. In order to perform this, the spectral optical coefficients (absorption and scattering coefficients) were calculated as a function of aspect ratio – i.e. ratio of length to diameter for GNR – with a volume fraction of 0.001% in a medium of refractive index 1.33 (water) and are shown in Figure 2.

Figure 2. Variation in (a) absorption coefficient, and (b) scattering coefficient of GNR as a function of incident radiation wavelength for three different values of aspect ratio (3, 5 and 7). The nanoparticle volume fraction and refractive index of medium are considered to be equal to 0.001% and 1.33 respectively. Diameter of nanorod is taken as 5 nm.

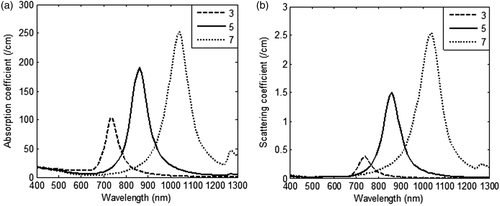
Figure 2 shows that by varying the aspect ratio of GNR, it was possible to tune the optical absorption and plasmon peak shifts to near-IR region with increasing aspect ratio. GNR with aspect ratio of 3 gave an absorption and scattering coefficient of 100 1/cm and 0.37 1/cm respectively but with increasing aspect ratio, contribution of scattering rose dominantly as compared to absorption. As scattering does not contribute to heating, an aspect ratio of 3 was chosen for further calculations. The effect of GNR diameters (5–15 nm) on optical coefficients is shown in Figure 3. From Figure 3 it is inferred that on increasing the diameter of GNR from 5 nm to 15 nm, scattering coefficients increased approximately 76 times as compared to 1.7 times the increase in absorption coefficients. As absorption coefficients are solely responsible for heat generation, and scattering primarily redirects the light, it is preferred to have minimal scattering to achieve tumour-specific heating. Also, our calculations show that by increasing the refractive index of the medium to 1.45 (∼skin tissue) the absorption peak shifted from 735 nm to 770 nm, but the magnitude of absorption coefficient remained the same at 103 1/cm for GNR of 5 nm diameter. Since the refractive index of body tissues varies from 1.33–1.65 as per tissue type and wavelength, a broadband radiation source will capture the energy absorption more effectively as compared to a monochromatic laser. Also, a broadband radiation source will efficiently exploit the broad plasmon absorption band of GNR. For various diameters of GNR, the relative contribution of absorption (Q_abs) and scattering efficiencies (Q_sca) and scattered intensity profile are shown in Figure 4.

Figure 3. Variation in (a) absorption coefficient, and (b) scattering coefficient of GNR as a function of incident radiation wavelength for three different values of GNR diameters (5 nm, 10 nm and 15 nm). The nanoparticle volume fraction and refractive index of medium are considered to be equal to 0.001% and 1.33 respectively. Aspect ratio is taken as 3.

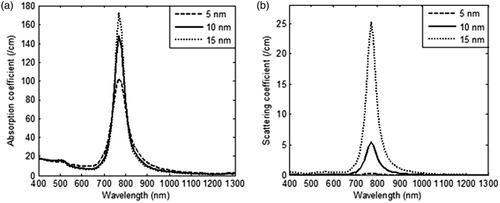
Figure 4. Variation in (a) relative contribution of absorption and scattering efficiencies as a function of incident radiation wavelength, and (b) intensity scattered at the plasmon wavelength in the GNR embedded domain; for three different values of GNR diameters (5 nm, 10 nm and 15 nm). The nanoparticle volume fraction and refractive index of medium are considered to be equal to 0.001% and 1.45 respectively. Aspect ratio of GNR and incident intensity is taken as 3 and 100 W/m²-nm for duration of 125 s respectively.

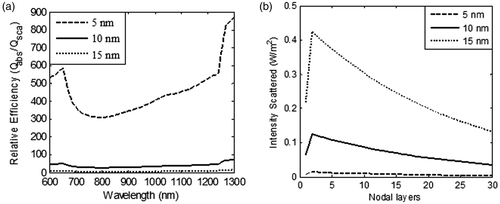
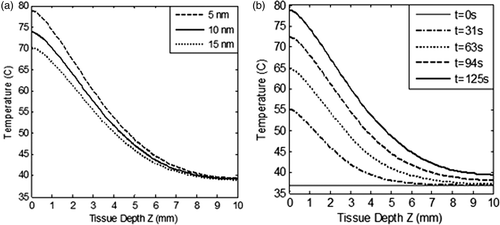
From Figure 4, it is clear that lower diameter GNR had the highest absorption to scattering ratio, thus justifying their candidature for selection as photothermal agents. The role of particle diameter on spatial temperature attained was evaluated for GNR diameters of 5 nm, 10 nm and 15 nm and the results are illustrated in Figure 5A. These results show that lower particle size tended to produce slightly higher temperatures within the tissue region. Figure 5B shows the spatio-temporal field for 5-nm diameter GNR upon irradiation with intensity of 100 W/m²-nm for a duration of 125 s. For 5 nm GNR, the spatio-temporal temperature field was independent of scattering coefficients as 5-nm diameter GNR scattered almost zero incident radiation as per the results shown in Figure 4B. Thus, use of 5-nm diameter GNR would result in more target-specific heating as there was no redirection of light due to scattering. Figure 5A shows that peak surface temperature fell by ∼8°C for 15-nm diameter GNR due to a higher scattering coefficient. On further increasing the diameter of GNR, this temperature difference would be more, so a GNR diameter of 5 nm was selected for evaluating the effect of other parameters discussed in this study. Also, this can lead to highly absorption-dominated medium and avoids spatial scattering of light, which otherwise leads to non-confinement of heat to the tumour zone. The lower GNR diameter limit was taken as 5 nm because synthesis of smaller GNR particles is difficult and quantum effects prevail around 1–2 nm. Thus, the modelling predictions of optical coefficients may not be valid for particles with diameters below 5 nm. Considering the results discussed so far, a GNR diameter of 5 nm is the preferred choice to minimise scattering of incident energy and thus achieve tumour-specific heating (to confine heat to the tumour zone as well as for efficient photothermal absorption of incident energy).

Figure 5. Variation in (a) spatial temperature as a function of tissue depth for three different values of GNR diameters (5 nm, 10 nm and 15 nm), and (b) spatiotemporal temperature for GNR of 5 nm diameter as a function of tissue depth. The nanoparticle volume fraction and refractive index of medium are considered to be equal to 0.001% and 1.45 respectively. Aspect ratio of GNR and incident intensity is considered as 3 and 100 W/m²-nm for duration of 125 s respectively. Tissue depth, Z = 0 to 3 mm, represents the tumour region.

Healthy tissue-sparing characteristics

In this section, healthy tissue-sparing characteristics are discussed considering the effects of irradiation intensity, irradiation duration and volume fraction of GNR. Net radiant energy input was kept constant and optical coefficients of 5-nm diameter GNR were used to model the temperature field. Figure 5B shows that the heat penetration to surrounding healthy tissue increased with increasing duration of irradiation. As per the results shown in Figure 5B, irradiation intensity of 100 W/m²-nm with duration of 125 s (which gives an ablation temperature of ∼60–78°C in the tumour zone) was selected for evaluating the temperature field and thus healthy tissue-sparing characteristics. Blood perfusion rate was considered variable as per the case of restricted perfusion discussed in the Theory and methods section. Figure 6A shows the temperature field attained in the tissue domain for three combinations of irradiation −100 W/m²-nm for 125 s; 50 W/m²-nm for 250 s; 25 W/m²-nm for 500 s. It may be noted that the net amount of incident energy remained constant in all these cases.

Figure 6. Variation of temperature within the tissue as a function of tissue depth (a) heating curves, and (b) cool-down until 500 s after irradiation is stopped. The tissue domain is irradiated with three combinations of incident radiation intensity and duration - 100 W/m²-nm for 125 s; 50 W/m²-nm for 250 s; 25 W/m²-nm for 500 s. The net amount of incident energy remains constant in these three combinations. GNR diameter and volume fraction is considered as 5 nm and 0.001% respectively. Blood perfusion rate is considered as per the case of restricted perfusion. Tissue depth, Z = 0 to 3 mm, represents the tumour region.

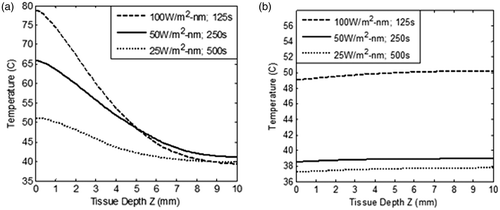
Analysing the results of Figure 6A, it can be seen that at an intensity of 100 W/m²-nm, surface temperature attained was ∼78°C. In the developed model, the maximum temperature in the tissue domain was restricted below 70°C as higher than this might lead to considerable change in the thermo-optical properties of the tissue. On the other hand, an intensity of 50 W/m²-nm for 250 s gave the required ablation temperature of 56–66°C in the tumour zone. By further lowering the intensity to 25 W/m²-nm and increasing irradiation time to 500 s, the required ablation temperature was not achieved throughout the tumour zone.

Once the irradiation is stopped, heat flow in the tissue domain may continue for some time due to the established temperature gradient. The spatial temperature attained during heating at various intensities was used as the input conditions to track cooling of the tissue immediately after irradiation was stopped. Figure 6B shows this temperature field once irradiation was turned off and the tissue was allowed to cool to ambient conditions. From Figure 6B, it is clear that by exposing the GNR embedded tissue to an irradiation level of 100 W/m²-nm for 125 s, the whole tissue attained a temperature of ∼50°C (after a time of 500 s), thus increasing the probability of damaging surrounding healthy tissue. But at an irradiation level of 50 W/m²-nm for 250 s, the whole tissue cooled down to a safe temperature of 38°C. Hence, the combination of irradiation intensity of 50 W/m²-nm for a duration of 250 s generated the required ablation temperature in the tumour zone, Figure 6A, as well as sparing surrounding healthy tissue, Figure 6B. As seen from Figures 6A and 6B, thermal conduction was overcome by natural convection for a surface temperature of 66°C. This did not happen for a surface temperature of 78°C. Higher surface temperature leads to deeper penetration of heat. Thus, heat penetration to the deeper tissue can be further controlled through forced convection at the tumour surface. To further ascertain the spatial extent/boundary of sparing the healthy tissue, the temperature versus time plots were generated at various tissue depths; at Z = 3 mm (tumour–healthy tissue boundary); at Z = 4 mm (1 mm away from tumour zone); and finally at Z = 5 mm (2 mm away from tumour zone), and are depicted in Figure 7.

Figure 7. Variation of the temperature within the tissue as a function of time at three depths (Z = 3 mm, 4 mm and 5 mm) in the tissue. Z = 3 mm represents tumour - healthy tissue boundary. GNR diameter and volume fraction is considered as 5 nm and 0.001% respectively. Tissue domain is irradiated with incident intensity of 50 W/m²-nm for duration of 250 s. Blood perfusion rate is considered as per the case of restricted perfusion. Z > 3 mm represents healthy tissue surrounding the tumour.

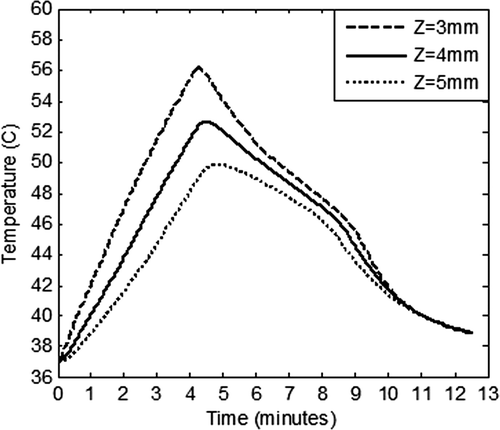
From Figure 7, it is clear that by exposing the GNR embedded tissue to irradiation level of 50 W/m²-nm for 250 s, the tumour–healthy tissue boundary (Z = 3 mm) attained a maximum temperature of 56°C during the heating cycle and a temperature of ≥50°C was maintained for 261 s (∼4.4 min). The temperature in the rest of the tumour zone (Z = 0 to 3 mm) was higher than that at the tumour–healthy tissue boundary, thus incurring damage throughout the tumour zone. Furthermore, at a depth of 4 mm, a temperature of ≥50°C was maintained for about 156 s (∼2.6 min), thus incurring some damage at this boundary. At a depth of 5 mm, the maximum temperature, attained momentarily, was 49°C and it fell to 44°C after a time span of 250 s (∼4 min). Hence at a tissue depth of 5 mm onwards, the healthy tissue was completely spared from damage. Temperature in the whole tissue domain fell to 39°C after a cool-down time of 500 s (∼8.3 min). Also, our calculations showed that though 100 W/m²-nm for 125 s achieved required ablation temperature in the tumour zone, it had poor surrounding healthy tissue-sparing characteristics as compared to an irradiation level of 50 W/m²-nm for 250 s.

The role of the GNR volume fraction on the tissue temperature was also simulated for evaluating healthy tissue-sparing characteristics. These results are shown in Figure 8 for GNR volume fractions ranging from 0.0002% to 0.005% and at irradiation intensity of 50 W/m²-nm for 250 s. GNRs of 5 nm diameter and restricted blood perfusion were considered in evaluating this effect of volume fraction.

Figure 8. Variation of temperature within the tissue as a function of tissue depth (a) heating curves, and (b) cool-down until 250 s after irradiation is stopped. For three different values of GNR volume fraction (0.0002%, 0.001% and 0.005%). Tissue domain is irradiated with incident intensity of 50 W/m²-nm for duration of 250 s. GNR diameter is considered as 5 nm and blood perfusion rate is varied as per the case of restricted perfusion. Tissue depth, Z = 0 to 3 mm, represents the tumour region.

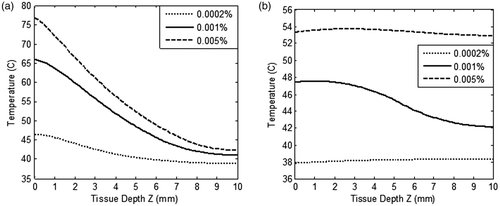
From the results of Figure 8A, as expected, the higher volume fraction of GNR resulted in higher temperature in the tissue domain due to considerable absorption of radiant energy. This was due to the fact that the optical absorption coefficient was directly proportional to the volume fraction. On increasing the volume fraction from 0.001% to 0.005% (by a factor of 5), surface temperature rose by 12°C. Also, heat penetration in the deeper tissue was significantly affected by increasing the volume fraction. By lowering the volume fraction to 0.0002%, the required ablation temperature was not achieved in the tumour zone. The effect of volume fraction on healthy tissue-sparing characteristics was further evaluated by modelling the tissue cool-down results once the irradiation was turned off. Figure 8B shows this temperature field in the tissue at a time instant of 250 s. From Figure 8B, it can be seen that the higher GNR volume fraction of 0.005% led to a temperature of more than 50°C in the healthy tissue region, thus damaging healthy tissue surrounding the tumour. Thus, under the conditions outlined in this study, it seems that a GNR volume fraction of 0.001% is optimum for achieving two goals – ablation of tumour tissue as well as sparing the surrounding healthy tissue. Hence, a combination of parameters, namely GNR diameter of 5 nm and volume fraction 0.001% irradiated with 50 W/m²-nm for 250 s, ablates the tumour region as well as spares the surrounding healthy tissue.

Conclusions

The numerical model developed in this study predicts the spatio-temporal temperature distribution in a tumour surrounded by healthy tissue during gold nanorod-assisted thermal therapy. This model also accounts for variation of the following important parameters: size and aspect ratio of gold nanorods, volume fraction, spectral irradiation intensity, and irradiation duration. Based on this model it was possible to determine an optimum combination for the parameters: 5-nm diameter gold nanorods, volume fraction of 0.001%, and irradiation intensity of 50 W/m²-nm for a duration of 250 s. Overall, it was found that under the conditions outlined in this study, these parameters allow the fulfilment of both goals outlined at the onset of the study – firstly that the tumour zone reached the ablation temperature (∼56–66°C) and was maintained ≥ 50°C for ∼4.4 min, and secondly the surrounding healthy tissue (2 mm beyond the tumour zone) incurred negligible damage. These results indicate that it is possible to achieve the right combination of parameters for a given geometry and blood perfusion rate. Thus, it is possible to use the model developed herein for a wide variety of thermal treatments using gold nanorods. The combination and range of parameters discussed here will also be useful to carry out future in vitro trials in this evolving research area. In this paper the penetration of the temperature within the GNR embedded tissue has been highlighted. In 2D or 3D cases the numerical results can be extended depending upon the known distribution of the GNR and spatial variation of radiation source.

In the model developed, uniform distribution of gold nanorods is assumed in the tissue. As GNR distribution in the tissue is dependent on delivery route and corresponding parameters, further work is required to assess and incorporate actual GNR distribution experimental data in the model. The effect of local tissue–blood interaction may be incorporated in future. Lastly, in vivo/in vitro experiments are needed to verify and validate these models.

Declaration of interest: S.S. and H.T. wish to acknowledge the support provided by the School of Mechanical, Materials & Energy Engineering at IIT Ropar. S.S. also acknowledges the support of CSIR-CSIO Chandigarh. The authors alone are responsible for the content and writing of the paper.