The impact of temperature and urinary constituents on urine viscosity and its relevance to bladder hyperthermia treatment

Abstract

Purpose: The aim of this study was to determine the kinematic viscosity of human urine and factors associated with its variability. This value is necessary for accurate modelling of fluid mechanics and heat transfer during hyperthermia treatments of bladder cancer.

Materials and methods: Urine samples from 64 patients undergoing routine clinical testing were subject to dipstick urinalysis and measurement of viscosity with a Cannon-Fenske viscometer. Viscosity measurements were taken at relevant temperatures for hyperthermia studies: 20 °C (room temperature), 37 °C (body temperature), and 42 °C (clinical hyperthermia temperature). Factors that might affect viscosity were assessed, including glucosuria, haematuria, urinary tract infection status, ketonuria and proteinuria status. The correlation of urine specific gravity and viscosity was measured with Spearman’s rho.

Results: Urine kinematic viscosity at 20 °C was 1.0700 cSt (standard deviation (SD) = 0.1076), at 37 °C 0.8293 cSt (SD = 0.0851), and at 42 °C 0.6928 cSt (SD = 0.0247). Proteinuria appeared to increase urine viscosity, whereas age, gender, urinary tract infection, glucosuria, ketonuria, and haematuria did not affect it. Urine specific gravity was only modestly correlated with urine viscosity at 20 °C (rho = 0.259), 37 °C (rho = 0.266), and 42 °C (rho = 0.255).

Conclusions: The kinematic viscosity of human urine is temperature dependent and higher than water. Urine specific gravity was not a good predictor of viscosity. Of factors that might affect urine viscosity, only proteinuria appeared to be clinically relevant. Estimates of urine viscosity provided in this manuscript may be useful for temperature modelling of bladder hyperthermia treatments with regard to correct prediction of the thermal conduction effects.

• Bladder hyperthermia
• thermal modelling
• treatment planning
• urine
• viscosity

Introduction

Bladder cancer is the fourth most common type of cancer in men and the ninth most common cancer in women in the USA [1]. Annually more than 50 000 men and 16 000 women are diagnosed with bladder cancer each year. More than 14 000 die annually of this disease. The most common type of bladder cancer, urothelial carcinoma, originates in cells lining the inside of the bladder and accounts for ∼90% of all bladder cancers. Bladder cancers are staged according to a standard tumour, lymph node, and metastasis (TNM) staging system: Ta, non-invasive; T1, invasive into lamina propria; T2, invasive into muscularis propria; T3, invasive into perivesical fat; and T4, invasive into adjacent organs. Two broad clinical phenotypes of bladder cancer exist: non-muscle invasive bladder cancer (Ta, T1) and muscle invasive bladder cancer (T2, T3, T4), and each is managed differently [2].

A hallmark of non-muscle invasive bladder cancer (NMIBC) is that it has a very high local recurrence rate, ranging from 40–80%, depending on individual prognostic factors. An important goal in managing bladder cancer is to develop treatments that reduce the risk of bladder cancer recurrences, which can occur repeatedly over many years. One such strategy that is being championed is bladder hyperthermia, a treatment where the bladder is heated to enhance the effectiveness of a chemotherapeutic agent filling the bladder lumen [3–5]. Bladder heating can be accomplished in many ways, including nanoparticle technologies. Hyperthermia has numerous effects on tumour microenvironment [6], but the most important known effect in bladder cancer is that it makes existing bladder chemotherapies more effective since elevated tissue temperature increases blood perfusion, permeability of blood vessel wall, tumour metabolic rate, and consequently drug uptake into the tumour cells [3].

Our group is interested in investigating novel minimally invasive methods of administering hyperthermia to the bladder. By heating with radio waves [4,5], the spatially dependent electromagnetic field will induce a spatially dependent heating pattern. This heterogeneous heating will induce convection currents within the urine that can be analysed using a computational conjugate heat-transfer model that includes both fluid dynamics and heat transfer physics [7]. This is a multi-physics problem where electromagnetic heating simulations require dielectric [8], thermal and biological properties [9]. For fluids it is also necessary to the initial pressure distribution and viscosity [10], which is not known with precision for urine [11–13].

Urine behaves as a Newtonian fluid [11,14], and as such, its fluid motion behaviour can be characterised by a single coefficient of viscosity which is temperature dependent. To our knowledge, only two works were published regarding urine viscosity, describing a variation from 0.787 cSt (SD = 0.098) at 37 °C [12], to 1.2–1.4 cSt in patients subjected to open-heart surgery, whose body temperature was likely less than 37 °C [11]. In these works the temperature dependency of urine viscosity was not evaluated. It should be noted that urine viscosity may increase considerably in pathologies [14]. Also, medications (e.g. dextrans) have been reported to change not only blood but also urine viscosity [12]. Hydration is another relevant factor [13].

Due to the lack of tissue property data, treatment planning for bladder hyperthermia has been addressed recently with an estimated ‘effective thermal conductivity’ parameter that seeks to mimic the combined effect of convection and conduction within the bladder urine and bladder wall [4]. This approach simplifies the thermal modelling by requiring simulation of only heat transfer, but this approach has not been validated for different bladder sizes and only accounts for a time average convection within the urine. By combining fluid dynamics and heat transfer analysis based on actual tissue properties, the temperature and heat flow at the bladder–urine interface may be characterised more accurately, allowing for better treatment planning.

Urine is predominantly water (91%), with small quantities of urea and other electrolytes [15], therefore previous computational models have assumed a urine viscosity close to water. We hypothesise that the viscosity of urine is temperature dependent and that it might vary under differing states of hydration, infection, or when blood is present. The goal of the current study is to characterise the viscosity of urine in a clinically significant range of temperatures, using a convenience sample of patients undergoing routine urine testing and to determine potential causes of its variability. Ultimately, these studies will provide better estimation of convection patterns and consequently thermal dose delivered to the bladder wall during hyperthermia treatments.

Materials and methods

Patient samples

After obtaining Institutional Review Board (IRB) approval, totally de-identified (all 18 Health Insurance Portability and Accountability Act (HIPAA) identifiers removed, only age and gender recorded) urine samples were obtained from patients over 18 years of age undergoing routine clinical urine testing in the core clinical lab of our institution. As per routine clinical protocol, samples were immediately stored at 4 °C at the time of collection to preserve their integrity and immediately transported to the clinical lab for testing. After clinical testing was complete, the remaining waste urine was collected by our study team and was subject to the test procedures described below, done within 24 h of initial specimen collection.

Urine dipstick test

Each urine sample was first tested with a Siemens Multistix 10 specific gravity (SG) urine reagent strip (Siemens Healthcare Diagnostics, Camberley, UK) as per the product insert. Briefly, the reagent strip was dipped fully into the urine subsample and immediately withdrawn and blotted to remove excess urine. The strip was then manually read in a high light environment at 30 s (glucose, bilirubin), 40 s (ketones), 45 s (specific gravity), 60 s (blood, pH, protein, urobilinogen, nitrite) and 120 s (leucocytes). The lower bounds of sensitivity of the reagent strip are: glucose (4 mmol/L), bilirubin (7 µmol/L), ketones (0.5 mmol/L), haemoglobin (150 µg/L), protein (0.15 g/L), urobilinogen (3.2 µmol/L), nitrite (13 µmol/L) and leucocytes (5 cells/high powered field (HPF)). A specimen was considered to have urinary tract infection if either nitrite or leucocytes were positive, haematuria if any detectable haemoglobin was present, and proteinuria if any protein was detected. Urine dipstick testing is known to be a reliable method of ruling in and out urinary tract infection [16], proteinuria [17] and haematuria [18].

Urine viscosity measurement

Viscosity is a measure of a fluid’s resistance to flow. It can be measured and reported by the kinematic viscosity which is often referred to as diffusivity of momentum, since it is analogous to diffusivity of heat and mass. It is therefore used in dimensionless numbers which compare the ratio of diffusivities and hence the relative importance of different physical processes [19]. For Newtonian fluids such as urine, the absolute viscosity can be determined directly by the product of density and kinematic viscosity.

We measured kinematic viscosity using a calibrated size 25 Cannon-Fenske viscometer (Cannon Instrument, State College, PA, USA). The kinematic viscosity of each urine sample was measured at 20 °C (room temperature), 37 °C (body temperature) and 42 °C (clinical hyperthermia temperature) by multiplying the viscometer efflux time (s) by the calibrated viscometer coefficient and recorded in centistoke units (cSt; mm²/s). Pure water has a kinematic viscosity of 1.004 cSt at 20 °C, 0.695 cSt at 37 °C and 0.634 cSt at 42 °C [20]. The temperature-specific kinematic viscosities were obtained by placing urine-loaded viscometers in heated water baths and allowing them to equilibrate for at least 10 min at each temperature. Viscometers were cleaned as per manufacturer protocol before and/or after each sample run.

Statistical methods

Urine kinematic viscosity was examined by temperature using histograms and standard summary statistics, and since the data appeared to fit a normal distribution, parametric methods were used for most aspects of the analysis. Spearman’s rank correlation coefficient (rho) was used to measure correlations between ordinal urine analytes and urine viscosity [21], and the Wilcoxon rank sum test was used to test whether urine viscosity differed between patients with different urine compositions [22]. To determine whether age, gender, or certain urine analytes could predict urine viscosity, regression models were created. For continuous covariates, modelling was done with generalised additive regression models to address any potential covariate non-linearity [23]. All analyses were done with R 2.14.1 with MASS and mcgv packages installed [24].

Results

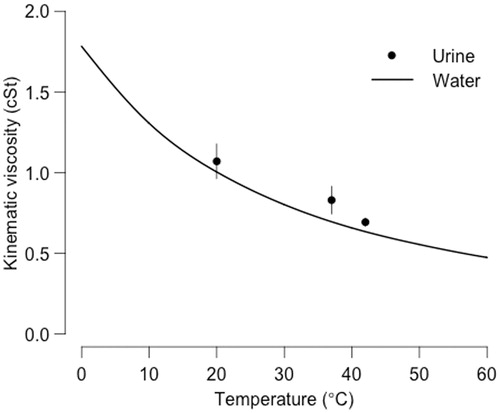
A total of 64 urine samples were examined from patients with a mean age of 51 years (SD = 15.1); 38 (59%) samples were obtained from male patients and 26 (41%) from female patients. Kinematic viscosity varied according to temperature and at 20 °C mean kinematic viscosity was 1.0700 cSt (SD = 0.1076); at 37 °C it was 0.8293 cSt (SD = 0.0851), and at 42 °C it was 0.6928 cSt (SD = 0.0247). While the kinematic viscosity of urine did decrease as temperature rose, it appeared to be significantly higher than that of water at all temperature points, particularly at body temperature (Figure 1). Plots and generalised additive models did not demonstrate any effect of age or gender on urine viscosity at any temperature.

Figure 1. Temperature dependency of the kinematic viscosity (in centistokes) of water (line) and urine (dots with standard deviation).

To assess whether common urine constituents might affect urine kinematic viscosity, we measured several different clinical parameters that characterise urine (Table 1). An elevated urobilinogen was found in only one patient, elevated glucose in four patients, and elevated ketones in five patients, raising the definite possibility of lack of statistical power to detect differences in urine viscosity for these urine constituents. Of the other more common constituents, proteinuria appeared to increase urine viscosity, whereas the presence of a urinary tract infection or haematuria did not.

Table 1. Impact of urine composition on median kinematic viscosity.

		Temperature
		20 °C		37 °C		42 °C
	N	Viscosity (cSt)	P value^a	Viscosity (cSt)	P value	Viscosity (cSt)	P value
UTI
Positive	12	1.0512	0.480	0.7976	0.048	0.6813	0.227
Negative	52	1.0533		0.8223		0.6947
Haemoglobin
Positive	18	1.0512	0.394	0.8038	0.258	0.6947	0.490
Negative	46	1.0533		0.8202		0.6906
Protein
Positive	13	1.0677	0.011	0.8161	0.546	0.7049	0.012
Negative	51	1.0471		0.8182		0.6864
Ketones
Positive	5	1.0533	0.388	0.8182	0.387	0.7152	0.186
Negative	59	1.0512		0.8140		0.6906
Glucose
Positive	4	1.1520	0.099	0.8459	0.481	0.7358	0.111
Negative	60	1.0512		0.8161		0.6906

^aWilcoxon rank sum test.

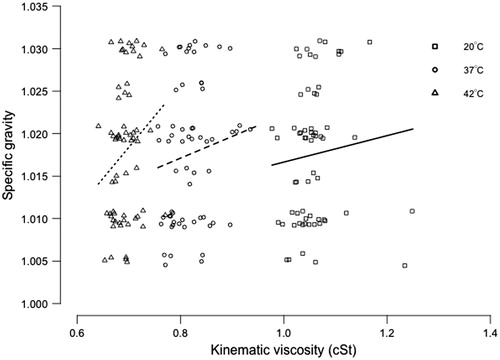
Lastly, we wanted to determine whether urine specific gravity was related to its kinematic viscosity and could serve as a simple surrogate. Urine specific gravity was moderately correlated with kinematic viscosity at 20 °C (rho = 0.259, p = 0.039), 37 °C (rho = 0.266, p = 0.035), and 42 °C (rho = 0.255, p = 0.044). However, jittered scatterplots demonstrate that this relationship was not particularly strong and suggest that urine specific gravity is not a sufficiently reliable surrogate of kinematic viscosity (Figure 2).

Figure 2. Scatterplot of urine kinematic viscosity (in centistokes) and specific gravity by temperature. Lines represent best least squares linear regressions for each temperature.

Discussion

The goal of this study was to provide estimates of urine kinematic viscosity as a function of temperature within a moderately hyperthermic range and under various commonly encountered clinical states, for use in treatment planning of bladder hyperthermia. Our principal findings are 1) urine kinematic viscosity is always higher (approximately 10% higher) than that of pure water within the interval 20–42 °C, 2) urine kinematic viscosity decreases with temperature, 3) proteinuria increases urine kinematic viscosity, and 4) urine specific gravity is not a surrogate for urine kinematic viscosity.

The fact that kinematic viscosity of urine decreases with temperature is not surprising since the viscosity of a Newtonian fluid – a fluid that flows irrespective of forces acting upon it (e.g. water) – is known to depend on temperature and pressure. However, we observed that the largest difference (19%) between water and urine viscosity was at body temperature (37 °C, Figure 1), suggesting that certain factors that affect the viscosity of urine behave differently at temperatures across the clinical spectrum from 20–42 °C. This was true, for example, in the case of proteinuria where we observed an increase in urine with rising protein levels at 20 °C and 42 °C but not at 37 °C. It is therefore possible that molecular biological interactions help maintain the viscosity of body fluids at normal body core temperature. The different temperature-dependent behaviour of urine in comparison with pure water indicates that water properties may not produce the same convection effects in the bladder and could potentially introduce errors in treatment planning of bladder cancer hyperthermia, though we did not specifically measure such effects in this study. While the urine viscosity measured at 37 °C is in the same range as published previously [12], the viscosity measurements at other temperatures are new findings.

Specific gravity is the ratio of the density of a liquid to the density of water and is therefore a dimensionless quantity and is related to the mass of solutes dissolved in the liquid. In the case of urine, specific gravity is a direct reflection of the concentration of the urine, which is itself relative to the metabolic state, the hydration level, and any existing urological pathology in the patient [25]. Urine specific gravity can be measured directly with gravimetry but is more typically measured indirectly using refractometry or reagent strips designed to capture ionic strength (such as the Multistix 10 SG strip used in the current study). These strips do not capture the impact of protein or glucose in their estimate of specific gravity and are sensitive to other urinary factors such as pH and the specific ionic composition of urine, making them somewhat unreliable [25,26]. Therefore, the fact that specific gravity was not a good predictor of urine viscosity in the current study (Figure 2) is not totally unexpected since it is a measure of urine concentration, not viscosity.

In contrast to serum viscosity, which has been more extensively examined, very few studies have evaluated factors that affect urine viscosity in humans. In rats it is known that radiological contrast agents can dramatically increase urine viscosity, something that undoubtedly also occurs in humans [27,28]. One human study also observed that urine viscosity increased in acute post-operative renal insufficiency and preceded multi-organ failure [11]. In the current study we observed that haematuria, urinary tract infection, ketonuria, glucosuria, age and gender did not appreciably affect urine viscosity but that the presence of proteinuria did. In agreement with these findings, Burton-Opitz observed that albuminuria was associated with increased urine viscosity [13]. Additionally, in the hyperviscosity syndrome that results from haematological malignancies and disorders, elevated serum protein levels lead to increased serum viscosity [29]. Like Burton-Opitz [13], we did not find that glucosuria affected urine viscosity. However, the number of patients with glucosuria in our study was small and the degree of glucosuria was mild, making our results difficult to generalise to patients with more elevated levels of urine glucose. Since hyperglycaemia does increase serum viscosity at biological temperatures [30], it is possible that our study was underpowered to detect this effect. Lastly, we were surprised to note that the presence of haematuria did not appreciably affect urine viscosity, particularly since red blood cell density (haematocrit) affects whole blood viscosity [31]. However, it is likely that the non-Newtonian effects of red blood cell interactions on whole blood viscosity may not be relevant in urine since the red blood cell density encountered in urine is markedly below that of whole blood. Perhaps with severe gross haematuria, which none of the patients in this study had, a more significant increase in urine viscosity would be found. This variability suggests that for a proper characterisation of urine’s viscosity it is important to document patient status and all relevant illnesses.

Conclusions

In the current study, urine kinematic viscosity did not vary by age, gender, glucosuria, urinary tract infection, or haematuria. Contrarily, proteinuria did appear to increase urine viscosity. The kinematic viscosity of human urine is temperature dependent and higher than water at all measured temperature points. Moreover, the change in urine viscosity as a function of temperature is significantly different than that of water, especially at 37 °C. Estimates of urine viscosity provided in this manuscript provide a better characterisation of the biological system and should result in more accurate modelling of bladder hyperthermia treatments.

Declaration of interest

This study was funded in part by Actium Biosystems (Boulder, CO, USA). The authors alone are responsible for the content and writing of the paper.