Development of a computational simulation tool to design a protocol for treating prostate tumours using transurethral laser photothermal therapy

Abstract

Objectives: The objective of this study was to design laser treatment protocols to induce sufficient thermal damage to a tumour embedded in a prostate model, while protecting the surrounding healthy tissue. Methods: A computational Monte Carlo simulation algorithm of light transport in a spherical prostatic tumour containing gold nanorods was developed to determine laser energy deposition. The laser energy absorption was then used to simulate temperature elevations in the tumour embedded in an elliptical human prostate model. The Arrhenius integral was coupled with the heat transfer model to identify heating protocols to induce 100% damage to the tumour, while resulting in less than 5% damage to the surrounding sensitive prostatic tissue. Results: Heating time to achieve 100% damage to the tumour was identified to be approximately 630 s when using a laser irradiance of 7 W/cm² incident on the prostatic urethral surface. Parametric studies were conducted to show how the local blood perfusion rate and urethral surface cooling affect the heating time to achieve the same thermal dosage. The heating time was shorter when cooling at the urethra was not applied and/or with heat-induced vasculature damage. The identified treatment protocols were acceptable since the calculated percentages of the damaged healthy tissue volume to the healthy prostatic volume were approximately 2%, less than the threshold of 5%. The approach and results from this study can be used to design individualised treatment protocols for patients suffering from prostatic cancer.

• Bioheat transfer
• gold nanorods
• laser photothermal therapy
• Monte Carlo simulation
• prostate cancer
• treatment protocol design

Introduction

The prostate gland is an essential component of the male reproductive system. As shown in Figure 1, the prostate is located below the bladder, surrounding the urethra. A normal prostate is slightly larger than a walnut [1]. In the absence of complications, the prostate will remain the same size for the duration of a lifespan [2]. Prostate cancer is associated with urinary dysfunction as the prostate gland surrounds the prostatic urethra. About 66% of patients diagnosed with prostate cancer have no symptoms, while one third have one or more symptoms including frequent urinations, nocturia, dysuria, haematuria, and sexual dysfunction [3–5]. Treatments for prostatic cancer are important to prevent metastasis in other parts of the body, as well as to improve quality of life for senior citizens.

Figure 1. Schematic diagram of laser photothermal therapy in treating prostatic cancer. A catheter with an embedded laser fibers is inserted through the prostatic urethra, supported by cooling water circulating inside the catheter to protect the urethra from overheating. Laser energy is emitted from the laser fiber to reach the tumor.

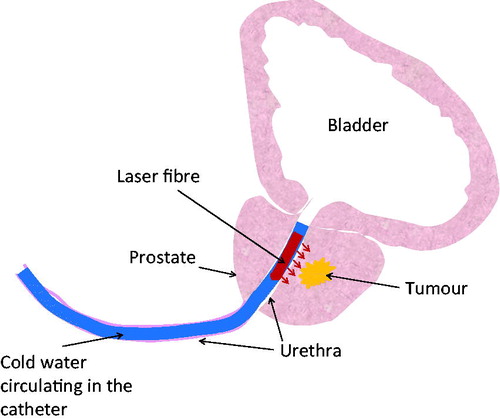
Laser photothermal therapy for prostate tumours or lesions may be an attractive alternative to surgical resection, due to its minimally invasive procedures and the possibility of performing it on patients when surgical complications are severe. Laser light offers an excellent means of inducing local temperature elevations in tissue, which can be explored for cancer therapy. A laser catheter can be introduced to prostatic tissue transurethrally and laser can emit from thin optical fibres, as shown in Figure 1. Depending on how deep the tumour is located from the prostatic urethra, laser energy can reach the targeted tumour to elevate its temperatures to achieve a desirable thermal dosage. Using gold nanorods as laser energy absorption enhancers can further confine laser energy to the tumours while minimising heat absorption in the surrounding healthy tissue. It is also possible to utilise cooling via cold water circulating inside the catheter to avoid thermal damage to the sensitive prostatic urethra during laser treatment. This technique has been widely seen in microwave and radio frequency hyperthermia in treatment for benign prostatic hyperplasia (BPH) or prostatic cancer [6,7].

The success of thermal dosimetric planning in laser photothermal therapy relies on accurate predictions of possible temperature elevations and duration of the therapy. Cell viability has a strong relationship with thermal stability of several critical proteins [8]. The temperature elevation history can then be used to assess thermal damage. Many researchers have been utilising temperature thresholds to predict lesion size and to define thermal injury [9–15]. The most common temperature thresholds assigned are 43 °C, 48 °C, 50 °C, and 60 °C [16–24]. In theory, thermal damage can occur at any temperature above 43 °C as long as the heating time is long enough.

Previous studies by our group have illustrated the possibility of elevating tumour temperatures above 50 °C in prostate tumours implanted on the flanks of nude mice using an amount of only 0.1 mL of gold nanorod solution [21]. The laser irradiance used in the experiments was also low, approximately 1.6 W/cm² with a total laser power of 0.5 W. The temperature profiles measured suggest that normal tumour tissue without nanorod presence still absorbed some amount of the laser energy; however, the injected nanorods in the tumour ensured that the majority of the laser energy was confined to the targeted tumour. That was also the first time showing the relatively uniform deposition of nanorods in tumours after their injection. Based on the measured temperature fields of the tumours, the radiation properties of PC3 tumours containing the gold nanorods were extracted for future theoretical simulations [25]. Unfortunately, the temperature elevations measured in the tumours implanted on the skin surface of the mice may be quite different from when the tumour is located inside the prostate, leading to different heating protocols being required to achieve the same thermal dosage.

The objective of this study was to develop theoretical models to design treatment protocols using transurethral laser photothermal therapy for prostate cancer patients. We proposed inserting a laser catheter into the prostatic urethra and a laser at 808 nm wavelength incident on the prostatic urethral surface, penetrating into the deep tissue with a targeted tumour embedded in the prostate. The tumour was injected with 0.1 mL of a gold nanorod solution, as in our previous studies [21,25]. The previously extracted optical properties of the prostatic tissue with or without gold nanorods were then used in a Monte Carlo simulation for predicting laser photon propagation in a multi-region tissue domain [25]. Mathematical formulation, finite element modelling of the heat transfer process, and possible thermal responses to heating were simulated, leading to thermal damage assessments and treatment protocol designs. The treatment protocol was accepted if the treatment resulted in 100% thermal damage to the targeted tumour with less than 5% collateral damage to the surrounding healthy tissue.

Methods

Geometrical description of the model

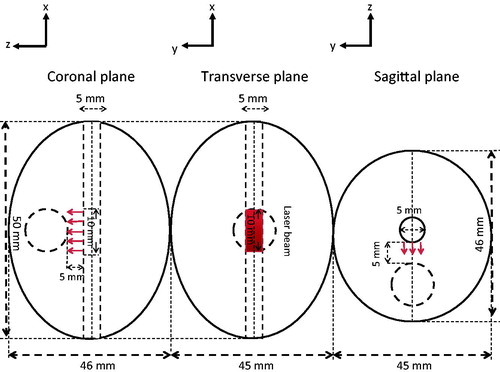
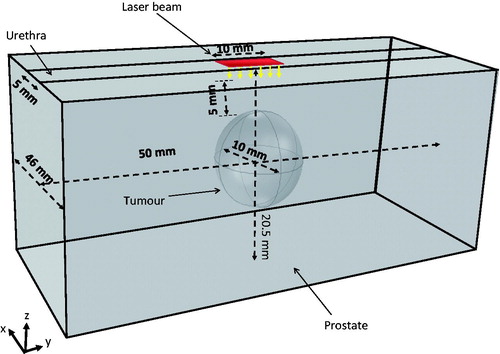
Geometrical representations of a human prostate are shown in Figure 2. The given dimensions of an ellipsoid with a height of 46 mm, a width of 50 mm, and a depth of 45 mm were based on simplifications of typical human prostates and the prostatic urethra [1]. A PC3 tumour was modelled as a sphere with a diameter of 10 mm and its centre was located 10 mm below the urethral path. A laser catheter was inserted into the prostatic urethra and laser irradiation at 808 nm wavelength occurred at a segment of the bottom surface of the urethra. In this model, the prostate and the embedded PC3 tumour had a total volume of 52.7 mL (excluding the urethra) and 0.523 mL, respectively. We equipped the laser catheter with a water cooling system to protect the urethral boundaries from overheating, see Figure 1. We also injected the prostate tumour with 0.1 mL of the 250 OD (optical density) gold nanorod solution used in our previous experiments [21,22,25].

Figure 2. The generated walnut shape prostate model and the embedded spherical tumour from three different perspectives.

Monte Carlo simulation

Before any heat transfer simulation was conducted, we determined the laser absorption distributions in both the prostate and the tumour regions. We used the Monte Carlo method to obtain the volumetric heat generation rate distribution [26–33]. Briefly, Monte Carlo simulations consist of photon weight initialisations, step size calculations, photon weight attenuation, and scattering trajectories of photons. Each photon was initially assigned a weight based on the laser irradiance incident on the top surface of the tissue, W₀. After the initial partial specular reflection on the top surface, calculation of the step size of the photon inside the tissue was calculated based on sampling of the probability for the photon’s free path, s(0,∞). According to the definitions of the absorption coefficient µ_a and scattering coefficient µ_s, the step size was determined by, where ζ is a random variable in (0, 1]. The amount of the photon weight attenuation, ΔW_i at location i, is calculated by,

The photon weight decreases from its previous value W_i to W_i+1,

Before the photon moves to its next location, scattering occurs so that the trajectory of the photon is determined by a deflection angle θ and an azimuthal angle Ψ from its previous path direction. A widely used probability distribution of the cosine of the deflection angle is given as where g is the anisotropic factor, and ζ is a random variable between (0, 1]. Ignoring the asymmetric scattering in the azimuthal direction gives a constant probability density function and an azimuthal angle Ψ that is uniformly distributed within the interval (0, 2π), i.e., Ψ = 2πζ.

Therefore, as the photon moves from one location to the next in the tissue, the absorption and scattering events occur and the photon weight decreases consequently. Finally the propagation of the photon is terminated when the photon weight is lower than a threshold value of 0.1% of its initial value or when a photon is out of the computational domain. In order to get statistically meaningful results, the trajectories of a large number of photons are simulated and the accumulated photon weight is stored in grid elements to calculate the volumetric heat generation rate distribution.

Special considerations involving multiple regions with different optical properties

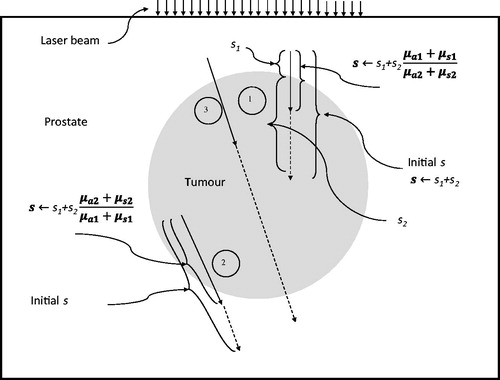
As shown in Figure 3, a photon’s propagation may involve more than two regions with different absorption and scattering coefficients. Considering the simulation path of photon 1 in Figure 3, it may initiate in the prostate tissue region but end in the tumour region injected with gold nanorods. A photon may start in the tumour region and end up in the prostate tissue region (photon 2 in Figure 3). The simulation for photon 3 in Figure 3 actually moves into three regions. For the photon path involving only one region, Equation 1 was used to calculate the step size of the photon. In the situation involving more than one region, modifications were needed, as suggested by previous studies [26,27]. For example, considering the simulation of photon 1 in Figure 3, since the absorption coefficient and scattering coefficient of the gold nanorod-injected tumour region were higher than that of the prostate tissue region, the step size inside the tumour region was shortened by a ratio of (µ_a1 + µ_s1)/(µ_a2 + µ_s2), where µ_a1 and µ_s1 are the absorption coefficient and scattering coefficient of the tissue region, while µ_a2 and µ_s2 are that of the gold nanorod-injected tumour region. In the meantime, photon 2 started from a region with higher absorption and scattering coefficients; the portion of the step size in the prostate tissue region was then prolonged by a ratio of (µ_a2 + µ_s2)/(µ_a1 + µ_s1). Similar treatment can be implemented for photon 3.

Figure 3. Modifications of photon step sizes involving multiple tissue regions.

Simulation parameters, geometry definition and assumptions

As shown in Figure 2(C), a laser catheter was in contact with the prostatic urethra that has a curvature. It would greatly add computational intensity if laser photons were incident on a curved surface. To simplify mathematical calculations, in this study we proposed a slightly modified geometry from the ellipsoidal shape illustrated in Figure 2. The top half of the ellipsoid was neglected in the Monte Carlo simulation since no photon entered. The bottom half of the ellipsoid was replaced by a rectangular column (50 mm × 46 mm × 20 mm), therefore, the laser photons were incident on a flat surface (1.0 cm long and 0.5 cm wide), which was part of the rectangular top surface, shown in Figure 4. The boundary surfaces of the rectangular column should not affect laser propagation significantly, since a very minor volumetric laser absorption rate would occur at the region near the boundary. Although not perfect, we believe that the calculated volumetric heat generation rate in the tumour and its surrounding region can still be used as the source term in the heat transfer simulation with reasonable accuracy, and it was also cost effective.

Figure 4. Geometric representation of the Monte Carlo simulation. The red rectangular surface shows the surface irradiated by the laser beam.

For this simulation we utilised the extracted optical properties of a PC3 tumour containing 0.1 mL of the 250 OD gold nanorod solution, and the optical properties of prostate tissue without gold nanorod presence. In-house MATLAB codes were written for the Monte Carlo simulation. The total incident laser power I₀ was uniformly incident on the rectangular area (5 mm × 10 mm) divided into N sub-surfaces (N = 861). The total number of photons projected onto each sub-surface, N₀, was 1000, with a total of 861 000 (N × N₀) photons used. Since all the photons should have the same initial weight, the initial weight of each photon (W) was then calculated as

The tumour volume was then divided into cubic elements. The deposited photon weights ΔW in each cubic element from all 861 000 photons were added together to calculate the total laser energy absorbed by that specific cubic element. Each cubic element was 250 × 250 × 250 µm³. The volumetric heat generation rate in a specific cubic element in the tumour in terms of W/m³ was then determined by dividing the deposited photon weight (W) in the specific cubic element by the cubic element volume (m³). Since the Monte Carlo method is a stochastic approach, a large number of photons were needed to obtain statistically repeatable results. The total number of photons incident on each sub-surface (N) was increased from 1000 to 2000 to test the sensitivity. The numerical simulations suggested a very small difference (less than 1%) in the average specific absorption rate (SAR) value resulting from the increase in the number of photons. We also tested the sensitivity of the element size by decreasing the grid size from 250 µm to 100 µm and found that it resulted in a difference of less than 4% in the average SAR.

Heat transfer model in COMSOL®

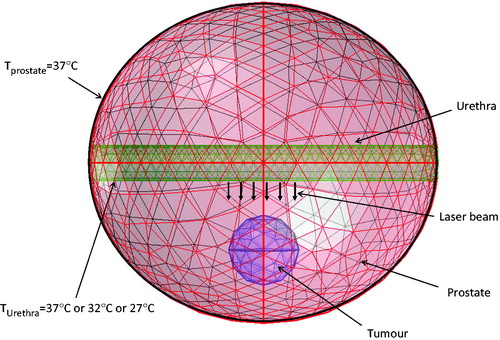
Figure 5 represents the frontal view of the meshed 3-D structure with assigned boundary and initial conditions. Tissue heat transfer due to the laser absorption is described by the Pennes bioheat equation [34], written as where T is the temperature, T_b is the temperature of the arterial blood and it is equal to 37 °C, k is the thermal conductivity, ρ_b is the blood density, c_b is the specific heat of blood, and Q_met is the metabolic heat generation rate. Note that the SAR, represented by Q_laser in Equations 6 and 7, was calculated from the Monte Carlo simulation in the previous section. The initial temperature condition for the prostate tissue was assumed to be at a body temperature of 37 °C. The circulating water in the laser catheter cooled down the prostatic urethra and its temperature was prescribed as either 37 °C, or 32 °C, or 27 °C to assess the cooling effect on the heat transfer in the prostate, as shown in Figure 5. At the outer surface of the prostate the temperature was prescribed as 37 °C.

Figure 5. Meshed finite element prostate model with corresponding boundary conditions.

The computations were conducted using COMSOL® 4.3 for the finite element simulation of the temperature field. The three-dimensional model was meshed with 14 369 quadratic tetrahedral elements. The simulation had a minimum element size of 9 × 10⁻⁴m and a maximum element size of 0.005 m, with an average growth rate of 1.769 and a total number of degrees of freedom of 41 922. We tested the sensitivity of the mesh size by increasing the total number of the elements by 280% and found that it resulted in a difference of less than 1% in the average tumour temperature.

Evaluation of thermal damage

Thermal damage in tissue can be described by a first-order thermal-chemical rate equation, in which temperature history determines damage. Damage is quantified using a single parameter Ω, calculated from the Arrhenius integral as follows [35,36]: where t is the time, C is the concentration of undamaged cells, A is the frequency factor (1/s), E_a is the activation energy barrier (J/mole), R_u is the universal gas constant (8.315 J/mole K), and T_t(x, y, z, τ) is the absolute tissue temperature at a location (x, y, z). The extent of damage is defined as the logarithm of the ratio of the initial concentration of the healthy cells, C(0), to the concentration of the healthy cells remaining after thermal treatment, C(t), for a duration of t (s). The value of Ω is zero before any thermal therapy, and it increases during heating; 99% denaturation of protein occurs when Ω = 4.

Dosimetric planning

The ultimate goal of any dosimetric planning in laser photothermal therapy is to predict extent of heat-induced necrosis [37]. Thermal damage depends on two major parameters: (1) the duration of heating, and (2) the temperature elevation. In an ideal thermal therapy for cancer treatment, the optimal treatment is to eradicate 100% cancerous cells and to preserve normal tissues with 0% damage. This was the basic principle for identifying constraints to achieve acceptable damage to normal tissue. In order to identify a treatment protocol, two criteria needed to be satisfied in this study: 100% volume damage to the tumour and less than 5% volume damage to the healthy tissue. Damage was defined as Ω ≥ 4.

The adjustable parameters were the laser power (or irradiance) and the heating time. In theory, thermal damage can occur at any temperature as long as the heating time is long. In this study we wanted to use the heating time as the only adjustable parameter while imposing a minimal tumour temperature in steady state. Based on previous studies [19,20,24,38], we assumed the minimal tumour temperature of 50 °C during steady state. This was achieved by adjusting the laser irradiance. Once the laser irradiance was identified, a time variant model was implemented in the COMSOL® software package to calculate simultaneously the temperature field and the thermal damage distribution in both the tumour and the prostate at any time point. The heating time needed to achieve a minimum Ω = 4 in the entire tumour was identified as the treatment time. Similarly, the thermal damage to the surrounding healthy tissue was assessed by the volumetric percentage of thermal damage to the healthy tissue. The percentage was calculated as follows: where V_Damage is the volume of thermally damaged healthy tissue, V_Prostate is the volume of one half of the prostatic tissue, and V_Tumour is the volume of the spherical tumour. If the percentage of tissue damage in the healthy region was less than 5% of the prostatic volume, the identified heating time was acceptable; otherwise, adjustment of the water temperature or other approaches had to be implemented to achieve the 5% minimal thermal damage to the healthy tissue.

Results

Monte Carlo simulation

For this simulation the laser irradiance to achieve a minimal steady-state temperature of 50 °C in the tumour was determined as 7 W/cm². All the other simulations are based on this laser irradiance value. Since the incident laser beam is a rectangular area of A = 0.5 cm², the total incident laser power can then be calculated as I₀ = 3.5 W. The anisotropic factor g is equal to 0.9 [33]. In our previous study we explained how the optical properties were extracted via comparing the theoretically predicted temperature profiles in the tumour to those measured in the in vivo experiments [25]. Table 1 gives a summary of the radiation properties of a PC3 tumour injected with 0.1 mL of 250 OD nanorod solution, and the prostate tissue without nanorods [25].

Table 1. Summary of the radiation properties used in Monte Carlo simulations.

Optical properties	g	μs (cm^−1)	μa (cm^−1)	μa/μs
Prostate region  (without gold nanorods)	0.9	5	0.41	0.082
Tumour region  (with gold nanorods)	0.9	7	1.1	0.157

The SAR distribution generated from the Monte Carlo simulation is depicted in Figure 6. Figure 6(A) shows the SAR contour map in the prostate model in the coronal plane, while the sagittal view of the SAR distribution is illustrated in Figure 6(B). To evaluate energy depositions within the tissue we divided the generated SAR into three regions: SAR₁ represents that within the spherical tumour, SAR₂ is confined to the laser spot area along the laser projection path in the healthy prostatic region, and SAR₃ is the rest of the prostate tissue. Figure 6(C) depicts the SAR distribution along the centre line in the z direction. There was some laser absorption in the prostate tissue; however, once the laser penetrated the tumour we observed large elevations in energy deposition in the tumour. The SAR in region 3 was very small compared to that in region 1 or region 2.

Figure 6. SAR contours in the prostate model in the coronal plane (A), sagittal plane (B), and the SAR distribution along the centre line (C).

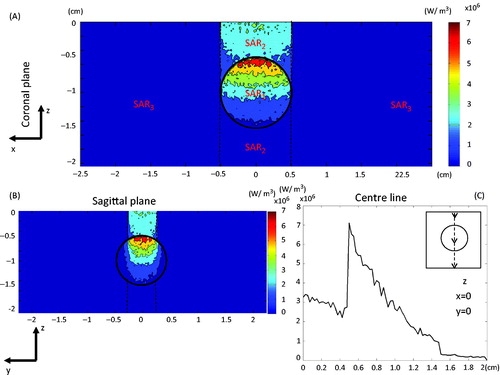
The maximum SAR induced by the proposed laser irradiance was 7.1 × 10⁶W/m³ in the tumour. Table 2 shows how the laser energy was conserved using the Monte Carlo simulation. It is evident that the enhanced absorption and scattering in the tumour not only increased the total amount of energy deposition in the tumour, but also altered the distribution of the energy. Adding the nanorods to the tumour increased the laser energy absorption (SAR₂) to approximately 26%, assuming that the tumour top surface was located 5 mm below the laser incident surface. Laser energy absorbed in region 1 (SAR₁) was 29%, and could not be avoided since the absorption coefficient was still approximately 36% of that in the tumour. Only 18% of the laser energy was confined to region 3 of the prostate tissue. The spectral reflectivity at the tumour surface was calculated as 0.0278, representing less than 3% of the initial photon weight. We also observed that 24% of the laser energy escaped from the calculated domain.

Table 2. Energy conservation in the Monte Carlo simulations.

	Absorbed by region 1	Absorbed by region 2	Absorbed by region 3	Escaped	Specularly reflected energy
Energy distribution	27.87%	26.36%	18.92%	24.07%	2.78%

Finite element analysis in COMSOL®

Once the SAR distribution within the prostate and tumour tissue was determined via the Monte Carlo simulation, a heat transfer model was developed to simulate the temperature field during laser photothermal therapy for treatment of the embedded prostatic tumour. The thermal and physiological properties obtained from the literature are given in Table 3. The thermal conductivity k (W/mK) and specific heat c (J/kgK) are typical values for prostate tissue [39–44]. Due to uncertainty of local blood perfusion responses to heating, two cases were simulated. One assumed a constant local blood perfusion rate during the heating. The other assumed that the blood perfusion in the tumour decreased with increases in temperature, possibly due to vascular damage during the heating. Thermal damage properties of the PC3 prostate tumour cells and native prostate cells in the Arrhenius integral were also considered temperature dependent [45], and they are listed in Table 4.

Table 3. Thermal and physiological properties of PC3 tumour and native prostate.

	Tumour	Prostate
Qmet (W/m^3)	2083	15333
ρ (kg/m^3)	1060	1060
k (W/m K)	0.5	0.5
c (J/kg K)	3780	3780
ω (s^−1)		0.00613
	Case 2: 0.000833

Table 4. Thermal damage properties for PC3 prostrate tumour cells, and native prostate cells corresponding to the laser wavelength of 810 nm.

Prostate cell type	Temperature range	Ru (J/K.mol)	Ea (J/mol)	A (1/s)
PC3	T > 54 °C	8.314847	1.24 × 10^5	7 × 10^17
	T ≤ 54 °C	8.314847	2.38 × 10^5	1.80 × 10^36
Native prostate	T > 54 °C	8.314847	5.88 × 10^4	5.65 × 10^7
	T ≤ 54 °C	8.314847	2.53 × 10^5	3.38 × 10^38

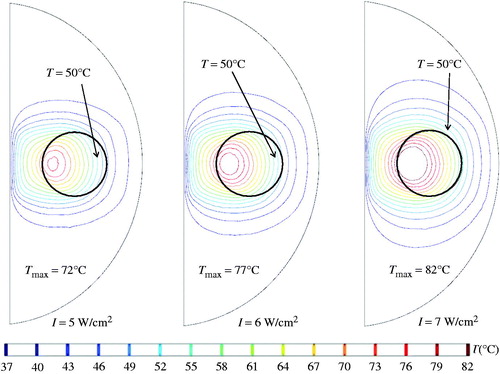
Figure 7 illustrates how different laser irradiances affected the steady-state temperature field. When the laser irradiance was selected as 7 W/cm², the steady-state temperatures inside the tumour were equal to or higher than 50 °C. The maximal temperature occurred in the tumour region, reaching 82 °C. Some regions of the prostate tissue also showed temperature elevations, reaching 76 °C outside the tumour region.

Figure 7. Coronal views of the steady-state temperature field under three different laser intensities.

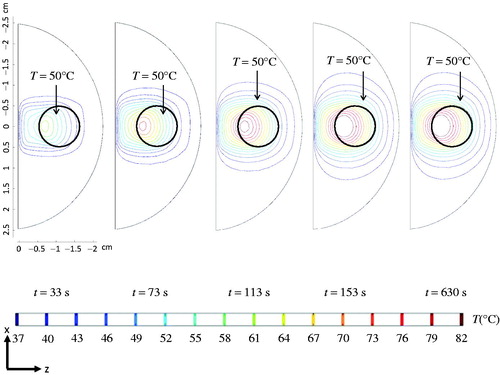
Once the laser irradiance of 7 W/cm² at the surface was identified, temperature transients were simulated to show its changes with time. The coronal views of the temperature contours at different time instants are presented in Figure 8. Note how the 50 °C isotherm extended to a bigger region when the heating time was longer. It only took 153 s for the temperature field to establish a steady state. Although cooling water was maintained at 37 °C at the urethral surface, the cooling did not penetrate very much into the deep prostate tissue to counteract the laser absorption in the prostate tissue near the urethra. The above simulations were based on a temperature-dependent ω.

Figure 8. Coronal views of the temperature contour evolutions for different time instants, assuming that the local blood perfusion rate is temperature-dependent.

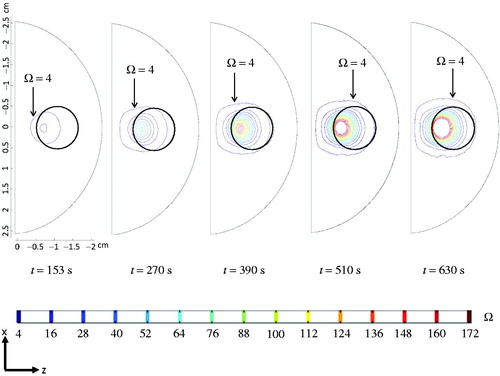
Figure 9 depicts the thermal damage contour evolution during the heating. After heating for 153 s, the thermally damaged tumour region (Ω ≥ 4) only consisted of 1/3 of the entire tumour, while 80% of the tumour was damaged after 270 s. After about 630 s (10.5 min) of heating, 100% of the tumour was damaged. Extensive injury also occurred in the healthy tissue region between the urethra and the top surface of the tumour. No damage was observed in the peripheral prostate tissue region. It is important to mention that although the steady-state temperature field had been achieved within 153 s, most of the thermal damage was accumulated after the steady state.

Figure 9. Coronal views of the thermal damage contours at different time instants, when the blood perfusion rate is assumed temperature-dependent.

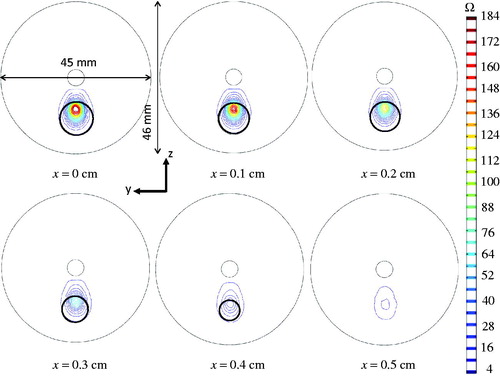
The sagittal views of the tissue region suffering thermal damage in several slices are shown in Figure 10. The black circle in each image represents the tumour boundary, as it got smaller moving away from its centre sagittal plane. We found that all the tumour tissue is within the Ω = 4 region on any sagittal slice at the end of the heating. Again, collateral thermal damage also occurred outside the tumour.

Figure 10. Sagittal views of the thermal damage at t = 630 s on different sagittal slices.

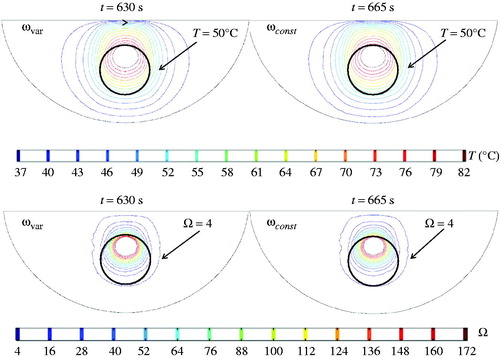
The effect of assuming a constant local blood perfusion rate on the heating time was examined in this study (Figure 11). It had a very minor effect on the minimal tumour temperature (50 °C) during steady state; therefore, the laser irradiance at the urethral surface was kept unchanged as 7 W/cm². It was identified that the heating time should be 665 s when ω was modelled as a constant during the treatment. The identified time was longer than that when ω was temperature-dependent. This may be largely due to the fact that an unchanged ω continued to act as a heat sink to the laser heating, therefore prolonging the heating time to achieve the same extent of thermal damage. On the other hand, the temperature-dependent ω model states that the local blood perfusion rate was only 50% of its initial value when the tumour temperature was higher than 42 °C, leading to higher temperature rises during later stages of the heating duration. The thermal damage contours again confirm that the entire tumour was within the Ω = 4 region for both blood perfusion cases.

Figure 11. Temperature and thermal damage contours at the end of the heating treatment: left panes represent that when the blood perfusion rate is temperature dependent, while the right panes give that when the blood perfusion rate is assumed unchanged during the treatment.

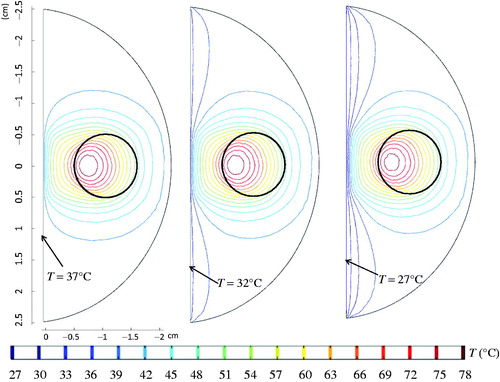
The last task of this study was to evaluate the effect of implementing different water-cooling temperatures at the urethral surface. The urethral temperature was assumed to be the same as the water temperature, prescribed as either 27 °C, or 32 °C, or 37 °C. The coronal views of the temperature contours are presented in Figure 12. A lower urethral temperature prescription pushed the isotherms of 37 °C, 39 °C, and 41 °C towards the deeper prostatic tissue region; however, it had relatively minor effects on isotherms of higher temperatures. Nevertheless, a decrease in the urethral surface temperature from 37 °C to 27 °C, resulted in a longer heating time by 17% to achieve the same thermal damage extent (739 s vs. 630 s).

Figure 12. The effect of the cold circulating water at the urethral surface on the temperature contours in the prostate.

Once the heating time was identified, the next step was to calculate the collateral thermal damage to the normal tissue. Table 5 gives the damaged volume in the healthy tissue (Ω ≥ 4), and the percentage of the damaged volume to one half of the prostate volume under different combinations of the urethral surface temperature and the local blood perfusion rate. Note that the damaged volumes of the healthy tissue in all cases were slightly larger than the tumour volume, varying from 0.552–0.653 mm³. The calculated percentages of the damage healthy tissue volume to one half of the healthy prostatic volume were approximately 2%, less than the threshold of 5%. Therefore, the identified heating time for each case was acceptable. In general, damage to the healthy tissue was smaller when tumour blood perfusion rate was kept as a constant than that when ω was temperature-dependent. Decreasing the temperature at the urethral surface not only protected the prostatic urethra from thermal damage, but also significantly lowered the temperature of the prostatic tissue close to the urethra when significant laser absorption occurred. As a consequence, thermal damage region was smaller (from 2.52% to 2.18%) in the prostatic tissue when the prostatic urethra was cooled. This looks like a very feasible approach to minimise thermal damage to healthy prostatic tissue.

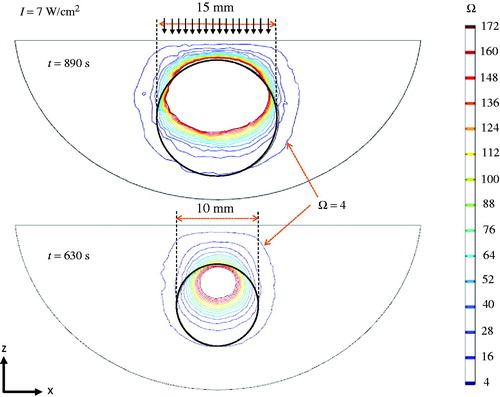
Table 5. Calculated damage volume, percentage of thermal damage, and designed heating time affected by combinations of local blood perfusion rate responses and urethral temperature.

ω (s^−1)	TUrethra (°C)	VDamage (mm^3)	Percentage	Heating time (s)
Constant	37	0.633	2.45	665
	32	0.563	2.18	777
	27	0.552	2.13	780
Temperature-dependent	37	0.653	2.52	630
	32	0.596	2.31	736
	27	0.564	2.18	739

The flexibility of the simulation tool is illustrated in Figure 13, which shows the thermal damage distribution of a larger tumour at the end of its designed heating protocol. The tumour size was increased from 10 mm to 15 mm, and its centre location inside the prostate was kept the same. Since the tumour was bigger in size, the width of the laser spot was also increased from 10 mm to 15 mm, while the laser irradiance at the prostatic urethra was kept the same at 7 W/cm². The simulation shows that the heating time should be longer than with the smaller tumour (890 s vs. 630 s). Illustrated by the top and bottom panels in the figure, the entire tumour is within the thermally damaged region defined as Ω ≥ 4.

Figure 13. Comparison of thermal damage distribution in tumours of different sizes (tumour diameter: 15 mm on the top panel and 10 mm on the bottom panel). The embedded spherical tumour is illustrated by the black circle.

Discussion

Laser photothermal therapy has the potential to damage entire prostatic tumours with minimal collateral damage. Transurethral or transrectal access to the prostate region by a catheter has been used in the past in microwave or radio-frequency heating for treating prostatic cancer or BPH. We speculated that implementing a laser fibre into a catheter is a feasible approach to take advantage of laser energy confinement by gold nanorods. Temperature elevations in tumours can be achieved via laser energy emitted from a laser catheter inserted in the prostatic urethra. In addition, cooling using cold water circulating inside the catheter has been developed in the past to protect the sensitive prostatic urethra in microwave or radio-frequency heating applications [6,7]. Further, thermal damage to the important neurovascular bundle is unlikely when using this approach, since the bundle is located at the outer surface of the prostate. As shown in previous studies, utilising near-infrared laser at 808 nm wavelength provided the advantage of minimising laser energy absorption by prostatic tissue near the prostatic urethra, while injecting gold nanorods into tumours, maximising laser energy absorption. This goal can be achieved by carefully designing heating protocols via theoretical simulations before actual laser treatment. The current study established a streamline process leading to identifying heating protocols using laser photothermal therapy. For a tumour located 10 mm below the prostatic urethra, the simulation treatment protocol designed has shown that collateral damage to the surrounding tissue would be below the 5% volume threshold. In addition to the heating duration, the laser power and the incident laser area can also become adjustable parameters to identify treatment protocols to assure effectiveness and safety. With advancements in computational resources, we envision that a simulation plan can be conducted within reasonable time before the actual heating session.

It is important to point out that the thermal treatment planning developed is the first step leading to practical clinical approaches and there is a lot of research ahead of us to further evaluate the clinical efficacy of laser photothermal therapy. It is well known that prostate cancer is a multi-focal disease. A review by Polascik et al. [46] has shown that the average number of individual tumours within human prostatic tissue is seven, spreading within the prostate at the time of radical prostatectomy procedures. When dealing with multiple tumours spreading in the prostate, the usual treatment approach is to resect the entire prostate. If laser photothermal therapy is used to treat prostatic cancer, it will be a challenge to develop a treatment plan involving multiple heating sessions focused on different tumours in individual sessions. From a practical point of view, laser photothermal therapy may be more suitable for BPH or when the prostatic cancer is in its early stages with fewer tumours and they are located close to one other. Further, it may be considered as an alternative when the patient cannot be subjected to surgical procedures or the surgical complications involve inevitable damage to the neurovascular bundle.

One improvement of our study is in the Monte Carlo simulation conducted in geometries with regular shapes. Since tumours growing in human prostates may have different shapes and sizes, it would be very helpful to perform Monte Carlo simulation on tumour geometry based on MRI or CT scans of targeted tumours. It is impossible to achieve individualised heating protocol design without considering patient-specific tumour sizes and shapes. In addition, the relative location of the PC3 tumour in the prostate is also a very important factor that may affect the thermal dosage deposited in tumours. The developed simulation tool in this study will be further improved by having the flexibility to predict tumour-specific treatment plans.

This study was based on a developed walnut-shaped human prostate model with a spherical tumour embedded. It was assumed that laser could be induced to the prostatic urethral surface via insertion of a laser catheter with cold water circulation in the catheter. Inserting a catheter with circulating water to the human urethra is nothing new, as shown in previous microwave heating devices for treating BPH or prostatic cancer. However, the proposed model was based on an assumed laser device that has not yet been developed in the market. Future research can be focused on developing such laser devices to be used in animal and clinical settings. As is true in any theoretical simulation, it is always important to validate a theoretical model via animal or clinical experiments. Once the laser catheter has been developed, temperature elevations inside a prostate can be recorded and compared to that predicted by the model. In addition, following a designed heating plan one can monitor tumour shrinkages after the heat treatment or perform histological analyses of the tumour tissue to confirm thermal damage to the tumour tissue. In the meantime, our theoretical models will be further improved based on the actual laser catheter geometry and its cooling and heating capabilities. For example, how the laser fibre is incorporated into a laser catheter with circulating water depends on technical advancement in the field. Laser energy may not penetrate the urethra without being diffused. Therefore, the exact laser photon propagations through the urethra and further into the prostate and tumour tissue require investigations based on the laser catheter once it has been developed.

In summary, we have developed a prostatic model with an embedded spherical prostatic tumour. Monte Carlo photon propagations and heat transfer in the prostate during laser photothermal therapy have been simulated to show temperature transients during heating and the resultant thermal damage accumulation with time. The simulation results allowed us to identify a feasible laser irradiance incident on the prostatic urethra, and a desirable heating duration to achieve 100% thermal damage to the embedded tumour and damage to less than 5% of the healthy prostatic tissue volume. Parametric studies have also been conducted to show how local blood perfusion responses and cooling at the urethral surface affect the heating time to achieve the same thermal dosage.

Declaration of interest

This research was supported by a National Science Foundation research grant CBET-1335958. The research was performed in partial fulfilment of the requirements from the University of Maryland Baltimore County for a doctoral degree by Navid Manuchehrabadi. The authors alone are responsible for the content and writing of the paper.