Study of the relationship between the target tissue necrosis volume and the target tissue size in liver tumours using two-compartment finite element RFA modelling

Abstract

Purpose: The aim of this study was to investigate the relationship between the target tissue necrosis volume and the target tissue size during the radiofrequency ablation (RFA) procedure.

Materials and methods: The target tissues with four different sizes (d_xy = 20, 25, 30 and 35 mm) were modelled using a two-compartment radiofrequency ablation model. Different voltages were applied to seek the maximum target tissue necrosis volume for each target tissue size. The first roll-off occurrence or the standard ablation time (12 min) was taken as the sign for the termination of the RFA procedure.

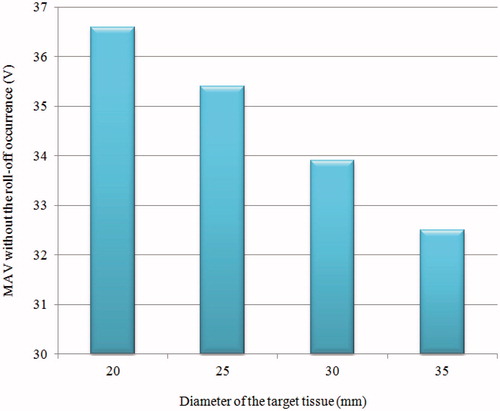
Results: Four different maximum voltages without the roll-off occurrence were found for the four different sizes of target tissues (d_xy = 20, 25, 30 and 35 mm), and they were 36.6, 35.4, 33.9 and 32.5 V, respectively. The target tissues with diameters of 20, 25 mm can be cleanly ablated at their own maximum voltages applied (MVA) but the same finding was not found for the 35-mm target tissue. For the target tissue with diameter of 30 mm, the 50 °C isothermal contour (IT50) result showed that the target tissue can be cleanly ablated, but the same result did not show in the Arrhenius damage model result. Furthermore, two optimal RFA protocols with a minimal thermal damage to the healthy tissues were found for the target tissues with diameters of 20 and 25 mm, respectively.

Conclusions: The study suggests that target tissues of different sizes should be treated with different RFA protocols. The maximum target tissue volume was achieved with the MVA without the roll-off occurrence for each target tissue size when a constant RF power supply was used.

• Finite element analysis
• Liver tumour
• radiofrequency ablation
• roll-off occurrence
• target tissue necrosis

Introduction

Radiofrequency ablation (RFA) has been used as an important treatment modality for various tumours and dysfunctional tissues, such as liver [1], lung [2], breast [3], kidney [4] and cardiac arrhythmias [5] because of its minimally invasive nature. As a sub-ablative thermal therapy, RFA is also used to treat hyperopia [6], hyperopic astigmatism [7] and presbyopia [6,8]. In recent years RFA for immune therapy has also attracted some attention [9–11].

However, RFA has a low success rate in ablation for tumours larger than 3 cm in diameter, which seems likely to be related to the limit in target tissue necrosis (TTN) volume. Xu et al. [12] reported that the complete ablation rate in tumours ≤3 cm was 95.4% after an initial RFA treatment for hepatocellular carcinoma (HCC). However, the same rates in tumours between 3.1 to 5.0 cm and >5 cm were only 82.5% and 50%, respectively. Shiina et al. [13] also found that the 5-year survival rate of HCC after RFA treatment was only 46.5% for large liver tumours (>3 cm in diameter). The same result also can be found in the literature [14,15]. It is widely suggested that this limitation is due to the charring of the target tissue.

The engineering pathway of tissue charring is as follows: The RFA procedure establishes a circuit with a power source (RF power generator) and a resistor contributed by the RF electrode, target tissue and ground pads [16]. The electrical conductivity of the target tissue, which depends on the water content and cellular make-up, is not a constant value. When the temperature of the tissue is higher than 100 °C the water essentially boils and begins to evaporate [17], the tissue becomes desiccated, and thus the target tissue becomes charred. The charred tissue further leads to a notable decrease in its electrical conductivity. This situation is observed in the clinical setting and is termed ‘roll-off’, which is characterised by a marked growth in the impedance between the RF electrode and ground pads, and furthermore the actual output of the RF power drops.

The roll-off is a crucial situation in the RFA procedure. In the clinical setting, one of the most popular RF power supply algorithms is based on the roll-off occurrence. In particular, the RF power generator is usually turned off for a while after a roll-off occurs, and during the power off period there is a cooling process around the probe. Arata et al. [18] attempted to build the relationship between the roll-off and the tumour ablation response. These researchers used the roll-off as the end point for the RFA procedure for ablation of the hepatic tumours and found that the local recurrence rate at 6 months without the roll-off (45%) was higher than that with the roll-off (15%). They tended to consider the roll-off as a significant sign of local control in the RFA procedure. It is well known that the lower local recurrence is mainly attributed to the unclean ablation of target tissue [19]. Thus, the relationship between the roll-off and the TTN is crucial in the RFA procedure. Trujillo et al. [20] investigated the relationship between the roll-off occurrence and target tissue dehydration (charring) and concluded that the roll-off usually occurs at the moment at which the RF electrode is completely encircled by charred tissue.

Controlling the roll-off is obviously an important means to enlarge the TTN volume. Some RF electrodes do have designs to provide chilled fluid inside the RF electrode to delay the roll-off occurrence. According to Trujillo et al. [21], this approach cannot eliminate tissue charring but just shift the charred tissue 1–2 mm away from the RF electrode surface, which may further increases the TTN volume by 1–3 times compared to the no chilled fluid situation [22]. Other methods to delay the roll-off occurrence can be the infusion of hypertonic saline solution into the target tissue [23] and the pulsed RF power delivery technique [24].

To date, many studies have attempted to overcome the deficiency of the RFA technique, such as the design of the RF electrode (internal cooling electrode, cluster electrode, perfusion electrode or extendable electrode), the design of the RF power supply method (pulsed, consecutive or switching) and combination with other therapeutic methods (irreversible electroporation, radiotherapy or chemotherapy) [19]. However, the results achieved so far are still not good enough because the target tissue that can be killed is still relatively small in size, especially when a monopolar electrode is used.

Pursuing a large TTN volume with a monopolar electrode in a short ablation period is the ultimate objective in RFA procedure today. To reach this objective, many questions should be answered in advance. Among them is the impact of the target tissue size on the TTN volume. Understanding their relationship may give us a clue to overcome the deficiency of RFA in the treating of target tissues with large sizes. However, to the best of our knowledge, few studies have investigated this relationship. Therefore, it is our belief that any additional information about the RFA treatment for target tissues of different sizes would be very useful to control TTN volume.

In this study we attempted to investigate the relationship between the TTN volume and the target tissue size based on a two-compartment numerical model using the roll-off as the end point of the RFA procedure. In the following section the two-compartment RFA model used, the termination of computer simulation and the data collection are discussed in detail. The results with discussion are presented, and several conclusions that can be drawn from this study are detailed in the last section.

Materials and methods

Electro-thermal model of two-compartment RFA

RFA uses so-called frictional heating (also known as ‘resistive’ heating) generated by a high frequency alternating current ( = 350–500 kHz) to kill tumour cells [25,26]. Thus, two processes need to be considered in the mathematical modelling of RFA, namely 1) heat transfer in target tissue (biological tissue) and 2) spatial heat generation by the electrical current with high frequency.

For heat transfer in biological tissues in this study Pennes’ bioheat transfer equation [27] was used because it has computational efficiency and reasonable accuracy as well. In Pennes’ model the perfusion term was considered as an isotropic heat sink without considering temperature variations in the arterial and venous blood and the structure of the local vasculature, as shown in Equation 1 where ρ kg m⁻³ is the density, is the specific heat,  °C is the temperature, in the Cartesian coordinate system, denotes the analysed spatial domains, is the thermal conductivity, is the blood density, is the blood specific heat, is the blood perfusion rate, T_b is the temperature of the blood entering the tissue, is the volumetric heat generated by metabolism, which is negligible due to its small magnitude compared with the other terms in Equation 1 and is the spatial heat generated by the RF electrical current.

Due to the high frequency employed in the RFA and the relative small size of the work domain (RF electrode in this case), the biological tissue can be considered as a resistor only because the displacement of charges in the alternating current can be negligible. Thus, the spatial heat power generated by the electrical current can be calculated using a quasi-static approach, as shown in Equation 2 where is the current density, is the electric field intensity, is the electrical conductivity and is the applied voltage. The voltage can be evaluated using Laplace’s equation [28]:

Using the quasi-static approach, the value of the ‘direct-current’ (DC) voltage can be calculated from the model corresponding with the root mean squared (RMS) value of the RF voltage [29].

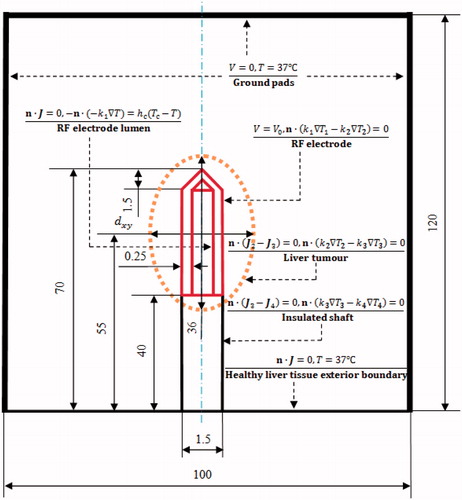
As shown in Figure 1, a healthy liver tissue was modelled as a cylinder with a diameter of 100 mm and a height of 120 mm. To consider the realistic clinical scenario, an elliptical liver tumour (HCC), 36 mm along the long axis, along the short axis (diameter of tumour tissue) was built in the centre of the healthy liver tissue. In the present study, liver tumours of four sizes, namely  = 20, 25, 30 and 35 mm, were considered as the target tissues. A 17-gauge (1.5 mm) internal cooling RF electrode with a 30-mm exposure length (Covidien AG, Zurich, Switzerland) was modelled and inserted into the centre of the liver tumour.

Figure 1. Dimensions (out of scale and in mm) and boundary conditions of the two-compartment RFA model used in the present study.

Finite element analysis of the two-compartment RFA model

The thermal conductivity, electrical conductivity and blood perfusion rate of the biological tissue were modelled as temperature dependent. The thermal conductivity was approximated with Equation 4 [30]. For the electrical conductivity, an increase of 2% °C was used in this study when the temperature was less than 100 °C. Between 100 and 105 °C the electrical conductivity exhibited a rapid decrease of two orders of magnitude due to water evaporation and desiccation [30], as shown in Equation 5. Because the frequency of the alternating current was not the research objective in this study, the dependence of electrical conductivity on frequency was ignored. The computation was fixed at a frequency of 460 kHz. There were some debates on how to model the blood perfusion of the biological tissue in the computational work. Most of the studies considered blood perfusion as a constant [31,32] or a piecewise function [33–35]. Some researchers [36] obtained a good agreement with in vivo animal experiments when using the foregoing constant method. It is worth mentioning that Schutt and Haemmerich [37] concluded that there were significant effects on TTN volume using different blood perfusion models. They used the piecewise model, a linear decreasing model, and a non-linear decreasing model. In the non-linear decreasing model they considered an increase of blood perfusion with an increase of degree of vascular stasis at the ablation zone boundary due to the hyperaemia. In the present study a piecewise function model of vascular coagulation was used. Particularly, the perfusion rate was considered as a constant before the biological tissue reached a temperature of 60 °C; at temperatures higher than 60 °C the blood perfusion rate was set to 0 because the coagulation eliminated microvascular perfusion [33]. Equation 6 shows the piecewise model of blood perfusion in the present study. where  = 21 °C, for the healthy liver tissue,  = 0.52 W m⁻¹K⁻¹ and  = 0.20 S m⁻¹ [38], whereas for the liver tumour,  = 0.60 W m⁻¹K⁻¹ and  = 0.50 S m⁻¹ [38,39]. The material properties used for each element are tabulated in Table 1. These values were adopted from the literature [38,40–44].

Table 1. Thermal and electrical properties of the modelling elements used in the present study.

Modelling element	Material	(kg m^−3)	C (J kg^−1K^−1)	k (W m^−1K^−1)	σ (S m^−1)	(kg m^−3s^−1)
Biological tissue	Healthy liver tissue	1080	3455	Equation 4	Equation 5	17.03
	Liver tumour	1045	3760			2.09
RF electrode	Ni-Ti	6450	840	18	1.0 × 10^8	–
Insulated shaft	Polyurethane	70	1045	0.026	1.0 × 10^−5	–
Blood vessel	Blood	1000	4180	0.49	0.667	–

The initial temperature was set to 37 °C. The electrical boundary was set as follows (Figure 1): (1) the RF electrode was set to a constant voltage () (Dirichlet) boundary condition, (2) a zero-electric-flux (Neumann) boundary condition was applied at the liver tissue exterior boundary, and (3) the ground pads were considered the other boundaries. The voltage at the ground pads was set to 0 V. Electrical continuity conditions were applied to the other inner boundaries of the whole two-compartment RFA model. The thermal boundary conditions were as follows: the liver tissue outer boundary temperature was 37 °C. The ‘heat-sink’ effect of the cooling effect of the chilled solution circulating inside the RF electrode was approximated by convective boundary conditions at the chilled fluid–electrode interface. Thus, the convective boundary condition of the chilled solution was realised by the heat transfer coefficient  = 4416.3 W m⁻²K⁻¹ and  = 10 °C. The heat transfer coefficient was calculated using Equation 7 [45]. where is the Reynolds number,  = 10.859 is the Prandtl number, D is the diameter and L is the length. For the chilled fluid circulating inside the RF electrode, which has a flow rate of 45 mL min⁻¹,  = 999.7 kg m⁻³, μ = 0.0013 kg m⁻¹s⁻¹, k = 0.588 W m⁻¹K⁻¹ and u = 0.9549 m s⁻¹ are the density, dynamic viscosity, thermal conductivity and average velocity of the fluid, respectively. The electrical and thermal boundary conditions on the four interfaces between liver tumour and healthy liver tissue, RF electrode and liver tumour, insulated shaft and liver tumour and insulated shaft and healthy liver tissue were considered as continuity, as shown in Figure 1.

The two-compartment RFA model was solved using the finite element (FE) software - COMSOL Multiphysics (Burlington, MA, USA). FE method was used to solve Equations 1–3 on the whole research domain as shown in Figure 1. The research domain was discretised into tetrahedral elements in this study. At every node of the tetrahedral element, Equations 1–3 were transferred to algebraic equations and these equations were solved by computer program. The FE mesh was generated by the free meshing generator within COMSOL. The mesh was progressively refined until the maximum temperature of RFA differed by less than 0.2 °C compared with the previous mesh. The previous mesh was considered the final mesh. The meshing results of the models of different target tissues with  = 20, 25, 30 and 35 mm were 282,867, 278,951, 280,787 and 285,765 tetrahedral elements, respectively.

The IT50 and the first-order kinetics model (Arrhenius damage model) were used to measure tissue death in this study. In the first-order kinetics model, the tissue death is related to the temperature and the ablation time using a first-order kinetics relation, as shown in Equation 8 where is the degree of tissue death, is the frequency factor, is the activation energy for the irreversible damage reaction, is the universal gas constant and is the absolute temperature, which is a function of the ablation time. The kinetic parameters A and ΔE account for the morphological changes in tissue related to the thermal degradation of proteins [46] and are dependent on the tissue type [47]. The two values (A = 7.390 × 10³⁹s⁻¹ and ΔE = 2.577 × 10⁵J mol⁻¹) for the healthy liver tissue were taken from the literature [48]. For the liver tumour tissue, A = 3.247 × 10⁴³s⁻¹ and ΔE = 2.814 × 10⁵J mol⁻¹ were taken from the literature [49]. The value of  = 1 (D63) was employed as the critical threshold to represent tissue death, which corresponds to a 63% probability of cell death [47]. At  < 1, the tissue was considered as live.

Computer simulation termination criteria and data collection

To simulate real clinical scenarios as closely as possible the standard RFA ablation time (12 min) was chosen, or the computer simulation terminates when the first roll-off occurs during the 12-min RFA. In this study we applied the finding reported by Trujill et al. [20] as the roll-off occurrence criterion, which considered that the roll-off occurs at the moment at which the RF electrode is completely encircled by the charred tissue (at 100 °C).

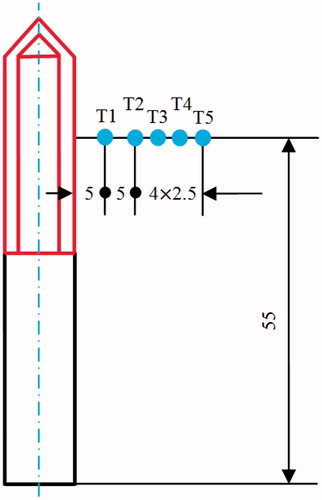
Five particular points were selected for the collection of the temperature data, as shown in Figure 2. Note that T2, T3, T4 and T5 were deliberately set on the boundaries of the four target tissues of different sizes ( = 20, 25, 30 and 35 mm, respectively). Thus, the complete TTN of each target tissue size can be investigated through an assessment of the temperatures at these particular points.

Figure 2. Placements of the five measured points (out of scale, dimension in mm).

The TTN volume in this study was the total volume of thermal damage (IT50 or D63) to the liver tissue, which was found by summation of the volumes of all tetrahedral elements in the liver tumour domain and the healthy liver tissue domain. The temperature on every node of such tetrahedral elements must be higher and equal to 50 °C or  = 1 on every node of such tetrahedral elements. The thermal damage volume to healthy liver tissue was found in the same way but just in the healthy liver tissue domain using  = 1.

Results and discussion

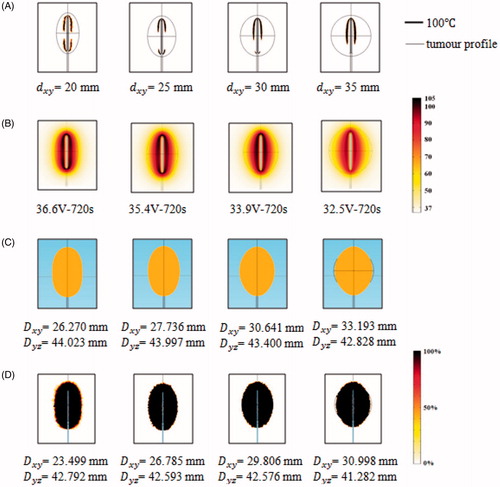
Table 2 shows the computer simulation results for the TTN area of each size of target tissue size at different voltages applied. The TTN area was found using the IT50 and the D63. and represent the longest length of the short (perpendicular to the RF electrode axis) and long (parallel to the RF electrode axis) axes of the TTN, respectively. All of the TTN were measured at the moment of the first roll-off occurrence or at 720 s, which was close to the clinical situation. For instance, 35 V–720s means that the voltage applied was 35 V and the TTN area was found at 720 s (note that no roll-off occurred at this voltage); 37 V–490s indicates that the voltage applied was 37 V and the TTN area was found at 490 s, which is the time when the first roll-off occurred. We found that the maximum value of can be achieved at a critical voltage. We also found that the critical voltage was the maximum voltage applied (MVA) at which the roll-off did not occur during a standard 12-min ablation time. It is necessary to note that all the MVAs were found using trial and error method and the accuracy of the MVAs was considered to be about 0.1 V.

Table 2. Computational results for four target tissue sizes during different RFA protocols.

Target tissue (mm)	Ablation protocol	Maximum temperature (°C)	IT50 (mm)	D63 (mm)	Complete ablation
= 20	35V–720s	105	= 23.445,  = 44.303	= 22.103,  = 42.491	Y
	36.6V–720s	105	= 26.270, Dyz = 44.023	= 23.499,  = 42.792	Y
	37V–490s	106	= 25.257,  = 43.814	= 22.562,  = 42.476	Y
	40V–170s	108	= 22.990,  = 43.165	= 18.312,  = 40.780	Y
= 25	34V–720s	104	= 26.729,  = 43.597	= 25.744,  = 42.050	Y
	35.4V–720s	105	= 27.736,  = 43.997	= 26.785,  = 42.593	Y
	36V–410s	107	= 27.057,  = 43.337	= 25.652,  = 41.611	Y
	38V–200s	108	= 25.419,  = 42.946	= 20.171,  = 40.771	N
= 30	32V–720s	104	= 29.196,  = 42.230	= 27.447,  = 41.772	N
	33.9V–720s	105	= 30.641,  = 43.400	= 29.806,  = 42.576	Y–N
	34V–620s	105	= 30.431,  = 43.208	= 28.340,  = 42.438	Y–N
	37V–185s	106	= 26.322,  = 42.407	= 19.802,  = 39.345	N
= 35	31V–720s	103	= 31.679,  = 41.846	= 29.527,  = 40.831	N
	32.5V–720s	104	= 33.193,  = 42.828	= 30.998,  = 41.282	N
	33V–525s	105	= 32.561,  = 42.818	= 20.431,  = 39.898	N
	35V–245s	107	= 28.893,  = 42.278	= 23.136,  = 40.462	N

Y: yes, N: no

Bold mean that the ablation protocols, which can achieve the largest TTN volume and complete TTN.

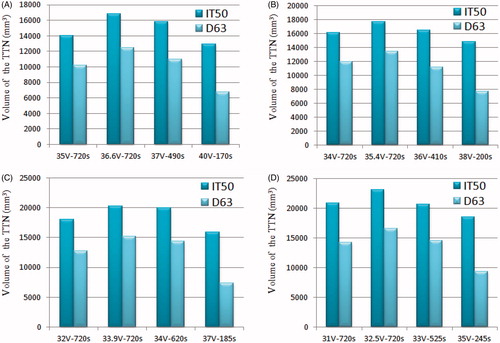
The same phenomenon can be found from the simulation results of the TTN volume. As shown in Figure 3, the TTN volume increases with the voltage and reaches the maximum value at the MVA and then decreases with the voltage. Due to the roll-off, a large TTN volume cannot be obtained by only increasing the voltage when a constant RF power supply is used.

Figure 3. TTN volume for each target tissue size at different voltages applied: (A)  = 20 mm, (B)  = 25 mm, (C)  = 30 mm and (D)  = 35 mm.

Another useful piece of information that can be observed from the results of this study is the change of MVAs for different target tissue sizes, as shown in Figure 4. We observed that the MVA decreases with an increase in the diameter of the target tissue because the target tissue that has higher thermal and electrical conductivities and lower blood perfusion is more sensitive to thermal therapy [43]. For the diameters  = 20, 25, 30 and 35 mm, the MVAs were 36.6, 35.4, 33.9 and 32.5 V, respectively. According to the results obtained in this study, it is worth mentioning that different RFA protocols should be adopted for different tumour sizes in the clinical setting. Thus, the same protocol is not the best choice for all clinical scenarios.

Figure 4. MVA without the roll-off occurrence for each target tissue size.

As shown in Figure 5, for small target tissues ( = 20 and 25 mm) complete TTN can be achieved at the MVA. However, for relatively large target tissue, such as  = 35 mm, complete TTN cannot be achieved at its MVA. This phenomenon indicates that this large target tissue is unable to be ablated cleanly using the constant RF power supply method alone. Some auxiliary methods, such as the pulsed RF power supply method [24] or the infusion of hypertonic saline solution into the target tissue [23,50], must be considered. For the critical size of target tissue, namely  = 30 mm, the IT50 result showed that the complete TTN can be obtained at the MVA, but the same finding was not demonstrated with the D63 result. It is noteworthy that the 30-mm diameter is a critical target tissue size for the prediction of whether the constant RF power supply method is suitable for RFA protocol. The results are also consistent with consensus in the field regarding RFA, which indicates that RFA alone is not effective for target tissues with diameters larger than 30 mm.

Figure 5. Computer simulation results for the TTN of target tissues of different sizes at the MVA (A) 100 °C isotherm, (B) temperature distribution (in °C), (C) tissue death (IT50) and (D) tissue death rate (%) (D63).

Minimal damage to the surrounding healthy tissue is also a critical requirement for RFA. In an ideal situation the target tissue should be completely removed (100%) but no surrounding healthy tissue should be removed (0%). In order to evaluate the thermal damage to the healthy liver tissue we proposed a volumetric percentage (VP) of the damaged healthy liver tissue, which is expressed by Equation 9 where is the volume of thermally damaged healthy liver tissue, is the volume of the liver tissue, is the volume of the liver tumour and is the volume of the healthy liver tissue. The VP of thermal damage to the healthy liver tissue for each RFA protocol is shown in Table 3. Although all the VPs were quite small (<1%), two optimal RFA protocols could be found for the 20-mm and 25-mm target tissues and they were 40 V–170s with 0.09% volumetric damage and 38 V–200s with 0.04% volumetric damage, respectively.

Table 3. Volumetric percentage of thermal damage to the healthy liver tissue during different RFA protocols.

Target tissue (mm)	Ablation protocol	(mm^3)	(mm^3)	VP (%)
= 20	35V–720s	934872.2	3093.9	0.33
	36.6V–720s		5416.9	0.58
	37V–490s		3854.1	0.41
	40V–170s		851.5	0.09
= 25	34V–720s	930631.0	1326.3	0.14
	35.4V–720s		2143.3	0.23
	36V–410s		1078.2	0.12
	38V–200s		397	0.04
= 30	32V–720s	925447.1	492	0.05
	33.9V–720s		1031.1	0.11
	34V–620s		861.4	0.09
	37V–185s		168.3	0.02
= 35	31V–720s	919321.0	347.2	0.03
	32.5V–720s		636.1	0.07
	33V–525s		466.5	0.05
	35V–245s		188.6	0.02

Bold mean the two optimal RFA protocols for the 20-mm and 25-mm target tissues, respectively.

Figure 6 shows the computationally determined temperature gradients for each target tissue size at its own MVA. The temperature differences between T1 and T2 decrease with the increase in the target tissue size, and the temperature differences range from 27.5 °C (Figure 6A) to 22.5 °C (Figure 6D) at 720 s. The temperature differences between T2 and T3, T3 and T4 and T4 and T5 become more uniform with an increase in the target tissue size. It is noteworthy that T2 through T5 are deliberately set at the boundaries of each target tissue. Using 50 °C as the standpoint for evaluating the TTN, we can find the following interesting conclusions.

Figure 6. Temperature change during the 12-min ablation procedure for each target tissue at its own MVA: (A)  = 20 mm, (B)  = 25 mm, (C)  = 30 mm and (D)  = 35 mm.

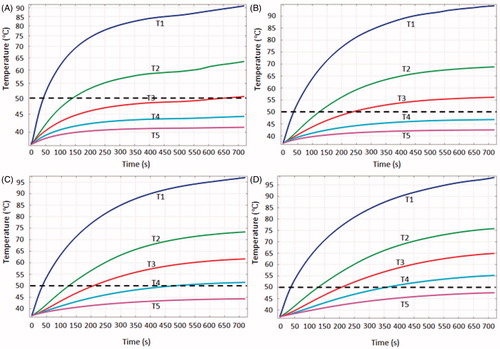
For target tissues with  = 20 and 25 mm, T2 and T3 were greater than 50 °C for 10 and 8 min respectively, which indicates that the specific target tissues have been ablated cleanly. For a target tissue with  = 30 mm, T4 was greater than 50 °C for more than 4 min. Thus, this target tissue can also be killed completely based on the 50 °C thermal criterion. However, for a target tissue with  = 35 mm, T5 never reached 50 °C throughout the 12-min RFA ablation period. The size of target tissue that can be ablated was larger than 30 mm, as shown in Figure 6(D).

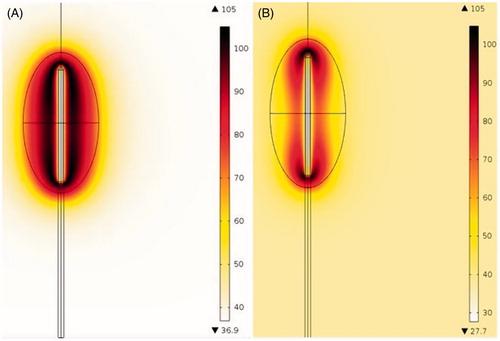
Figure 7 compares the temperature gradients obtained from the two-compartment RFA model and the one-compartment RFA model (homogenous RFA model). This result was simulated considering the 36.6 V–720s scenario, whereas for the homogenous RFA model, the electrical, thermal and perfusion properties were set equal to those of the healthy liver tissue. As shown in Figure 7, more biological tissues around the RF electrode were heated to a temperature greater than 80 °C with the two-compartment RFA model compared with those obtained with the homogenous RFA model. The 100 °C isotherm only appeared in a small area close to the distal and the proximal parts of the RF electrode in the homogenous RFA model. However, for the two-compartment model, the 100 °C isotherm almost encompassed the RF electrode. All of these differences prove that a more realistic RFA model should be considered when attempting to investigate the RFA technique using numerical modelling and computer simulation.

Figure 7. Temperature distributions (in °C) obtained with the two-compartment RFA model (A) and the homogenous RFA model (B).

One of the limitations of the present work could be the lack of experimental validation, but the authors are confident that the information presented in this manuscript is useful for understanding the deficiency of the RFA technique for the treatment of large tumour tissues and the effective treatment of target tissues of various sizes in clinical practice. The cooling effect of large blood vessels was also ignored in this study because the main objective focus was on target tissues of difference sizes. Another limitation is that we did not investigate the differences between the different types of liver tumours, such as malignant tumours and benign tumours, due to lack of data [51]. Our future and upcoming studies will aim to validate and improve the results presented in this manuscript using tumour tissue or tumour tissue phantom. Another interesting future work could be the investigation of the relationship between TTN size and target tissue size in pulsed RFA.

Conclusions

This study investigated the different results in the TTN volume on target tissues of different sizes using a two-compartment RFA model. The following three conclusions regarding the RFA procedure for the treatment of target tissues (liver tumours) can be drawn from the results of this study:

1. While using the constant RF power supply method, the largest TTN volume can be achieved at the maximum voltage applied without roll-off occurrence.

2. For target tissues of different sizes, the maximum voltage applied without roll-off occurrence is different and it decreases with an increase in the target tissue diameter.

3. The results predicted from the two-compartment RFA model are very different from those obtained with the homogenous RFA model.

Acknowledgements

This article was supported by the Saskatchewan Health Research Foundation (SHRF) through the ‘BioNEMS Phase I’ (grant no. 2539). This article was also supported by the National Natural Science Foundation of China (grant no. 51175179). The first author (Bing Zhang) also received financial support from the China Scholarship Council (CSC). Special thanks go to the anonymous reviewers’ comments on this paper, which helped to improve the paper considerably.

Declaration of interest

The authors report no conflicts of interest. The authors alone are responsible for the content and writing of the paper.