The influence of tumour blood perfusion variability on thermal damage during nanoparticle-assisted thermal therapy

Abstract

Purpose: This study investigates the influence of blood perfusion variability within a tumour and the surrounding healthy tissue during nanoparticle-assisted thermal therapy. It seeks to define ideal therapeutic parameters for a wide range of perfusion rates to attain the desired thermal damage. Material and methods: Pennes’ bioheat model and the Arrhenius model are used to evaluate the thermal damage for a two-dimensional tumour surrounded by healthy tissue. A wide range of tumour perfusion rates were modelled, ranging from moderate to high perfusion in both a homogenously and a heterogeneously perfused tumour. Results: For low perfusion rates, a temporal variation in blood perfusion does not critically influence the thermal damage. For moderately and highly perfused tumours, temporal variation in blood perfusion extends the thermal damage zone by 25–52% compared to a constant perfusion rate. For the tumour size and perfusion conditions under consideration, the ideal therapeutic parameters were found to be irradiation intensity of 1 W/cm², and irradiation duration of 105–150 s, for a nanoparticle volume fraction of 0.001%. Conclusions: It is concluded for low perfusion rates that due to shorter therapeutic duration, nanoparticle-assisted thermal therapy is relatively insensitive to changes in the perfusion rate during the therapy. For moderately and highly perfused tumours, a constant perfusion under-predicts the real thermal damage zone. This study concludes that for moderately and highly perfused tumours the spatial as well as temporal blood perfusion dynamics should be carefully accounted for to get a realistic estimate of thermal damage zone.

• Blood perfusion
• cancer
• nanoparticles
• thermal therapy
• vascular stasis

Introduction

Nanoparticle-assisted thermal therapy is evolving as a promising future treatment for cancer [1–5]. This therapy employs nanoparticles as heat sources within a tumour to selectively kill the tumour cells through thermal ablation [1,6]. This therapy utilises the wavelength band known as the ‘therapeutic window’ (600 nm–1300 nm) [7]. Within this wavelength band, the tissue absorbs radiation minimally while the nanoparticles strongly absorb it, thus considerably heating the tumour from within to cause thermal damage. Another important form of thermal therapy (currently undergoing clinical testing) utilises ferromagnetic nanoparticles to generate thermal energy for thermal ablation [8–10].

Blood flow within the tissue acts as a negative feedback mechanism to transfer heat away from the tissue to thermo-regulate healthy tissue [11]. Thus, blood flow significantly influences thermal ablation temperatures and the extent of thermal damage achieved within and around a tumour. Tumours are characterised by heterogeneous vasculature [12–14] and large variation of blood perfusion, even within tumours of the same type [15–18]. Additionally, during heating, temporal variation in the blood perfusion rate occurs as the body’s response to blood vessels experiencing thermal damage [19].

This issue of blood perfusion has been addressed widely for radiofrequency (RF) ablation and hyperthermia [15,20–22]. However, for nanoparticle-assisted thermal therapy, there exists little specific research that quantifies the role of blood perfusion. Given the considerably different heating regimes of this alternative treatment, a fundamental understanding of the influence of blood perfusion under typical nanoparticle-assisted therapy conditions is needed. This study represents the first effort in this direction and serves to quantify the extent of this issue by examining a wide range of parameters. Additionally, this research adds to further understanding in the area of gold nanorod-assisted thermal therapy [1–6,23]. As such, this study highlights the role of the spatio-temporal variability of blood perfusion within the tumour as well as the surrounding healthy tissue during these types of treatments. The temporal variation of blood perfusion is incorporated based on vascular stasis. The spatial variation of the perfusion rate is also incorporated by comparing a homogenously perfused tumour with a heterogeneously perfused tumour under similar irradiation conditions. The spatio-temporal thermal ablation temperatures and thermal damage are evaluated based on Pennes’ bioheat equation and the Arrhenius model. For each configuration, ideal therapeutic parameters (i.e. irradiation intensity and duration) and the corresponding temporal perfusion dynamics are highlighted.

Theory and methods

Skin tumour and blood perfusion variability

A two-dimensional cylindrical domain was assumed, as shown in Figure 1, approximating a typical skin tumour of 20 mm diameter and 5 mm depth. The tumour is surrounded by healthy tissue with10 mm radial thickness and a depth of 10 mm. The chosen tumour size corresponds to high risk skin cancers [24,25], which represents a set of good potential candidates for this type of treatment. The nanoparticles were assumed to be uniformly distributed (injected) within the 10 mm radius and 5 mm depth tumour region. Figure 1 is adapted from our previous work and the same two-dimensional domain is continued for the present study [23].

Figure 1. Schematic representing: (A) the tumour region surrounded by healthy skin tissue and (B) a symmetric R–Z cross-section of the tissue. The tumour is surrounded by healthy tissue of 5 mm thickness at the bottom and a 10 mm thick annulus. The symbols R and Z represent radius and depth of tissue, respectively. ΔR and ΔZ represent demarcations of the nodal region. T represents temperature at spatial location R, Z. (Figure reproduced from Soni et al. [23]).

The blood perfusion rate among tumours varies widely as compared to the tissue of origin. Depending on several factors, the perfusion rate can either be higher or lower than that of surrounding healthy tissue. A wide range of blood perfusion rates have been reported in the literature for the same tumour type [15,17,18,21,26]. For example, the perfusion rate in a breast tumour can vary by an order of magnitude from 5.3 × 10⁻³ to 5.3 × 10⁻² m³ s⁻¹ m⁻³ [16]. Further, the tumour blood flow can be modified through injection of certain agents such as hydralazine and phenylephrine [27]. Detailed studies have been presented on the tumour perfusion data [28,29].

Many of the published studies suggest that there is heterogeneous vasculature within a tumour – especially for large tumours. This results in a spatial heterogeneity of the blood perfusion. The literature also suggests that as a tumour grows, it develops a dead (necrotic) cell region at the core [14,28,30–32]. This is characterised by an absence of vasculature in this region and it is called necrotic core. Assuming this is the case, the blood perfusion in the core can be assumed to be negligible. The spatial extent (volume) of the necrotic core depends on the size of tumour.

In light of the wide range and variability of the available blood perfusion data, various perfusion conditions were included to investigate the effect of perfusion on thermal damage for the present study. Since there is so much variation in perfusion rates, this study intends to evaluate thermal damage by simply incorporating a broad range of reported perfusion data. Perfusion conditions for the case of a homogeneously perfused tumour are shown in Table 1. For the case of a heterogeneously perfused tumour, spatial variation of perfusion within the tumour is accounted for in the present model (for moderately and highly perfused tumours) by two methods: (1) different perfusion values in the tumour core and periphery, and (2) a necrotic (non-perfused) tumour core. For the tumour sizes considered in this study, the necrotic core is reportedly 40–50% of the tumour volume [30]. Thus, a tumour with a necrotic core of 50% of the total volume is assumed for this study. The perfusion values assumed for a heterogeneously perfused tumour are summarised in Table 2. During therapy, the blood perfusion rate varies as a function of vascular stasis (damage to the blood vessels), which is in turn a function of temperature and time.

Table 1. Blood perfusion values for a homogenously perfused tumour and tissue.

Perfusion	Tumour (m^3 s^−1 m^−3)	Normal tissue (m^3 s^−1 m^−3)
1. Low perfusion [26]	9.1 × 10^−4	1 × 10^−3
2. Moderate perfusion [18]	2.1 × 10^−2	4 × 10^−3
3. High perfusion [17]	5.3 × 10^−2	1 × 10^−2

Table 2. Spatial variation of blood perfusion (heterogeneously perfused tumour).

Blood perfusion	Tumour core (m^3 s^−1 m^−3)	Tumour periphery (m^3 s^−1 m^−3)	Normal tissue (m^3 s^−1 m^−3)
1. Moderately perfused tumour [15]	5 × 10^−4	1.7 × 10^−3	8.3 × 10^−3
2. Highly perfused tumour [27]	3.3 × 10^−2	4.8 × 10^−2	7.1 × 10^−3

Optical interaction of nanoparticle-embedded tumour

Gold nanoshells (GNSs) and nanorods (GNRs) are the most commonly studied particles for nanoparticle-assisted thermal therapy because they are biocompatible and their optical properties can be tuned [33–36]. In the present study GNRs were chosen as they possess up to six times higher absorbance than GNSs [2]. Size selection of the nanoparticles is critical as it governs the conversion of electromagnetic energy to thermal energy. In this study GNRs of 5 nm diameter and an aspect ratio of 3.5 were selected, based on our previous work [6]. This size ensures a much higher value of optical absorption relative to scattering. This is desirable as it will lead to efficient absorption at relatively low irradiation intensity levels. Optical absorption and scattering coefficients of GNRs (embedded with a volume fraction of 0.001% in tumour) were directly obtained from the earlier study [6]. A GNR volume fraction of 0.001% corresponds to a concentration of 0.19 mg/mL. The selected nanoparticle concentration is comparable with other published studies [2,37]. Details on the calculation of optical coefficients are also available in the study [6]. The addition of GNRs to the tumour results in a highly absorbing medium with a maximum absorption coefficient (μ_a) of 121 cm⁻¹ at the plasmon wavelength (796  nm). This is several orders of magnitude larger than the absorption value for the bare tumour (which is ∼0.06 cm⁻¹[38]). The reduced scattering coefficient (μ_s’) of a tumour is ∼0.5 times that of healthy tissue (which has a value of 3.25 cm⁻¹ [38,39]). This is due to the fact that a tumour scatters less than healthy tissue due to the lack of a well-differentiated structure [38]. The values of the optical coefficients used herein, along with other salient parameters, are given in Table 3.

Table 3. Symbols and values of the various parameters considered in this study.

Parameter	Value	Parameter	Value
Density of blood, ρb	1000 kg/m^3	Scattering cross-section of a single GNR, Csca	1.7 × 10^−18 m^2
Specific heat of blood, Cb	4200 J/kgK	Absorption coefficient of GNR, μabs	121/cm
Tissue density, ρtissue	1000 kg/m^3	Scattering coefficient of GNR, μsca	0.5/cm
Tumour density, ρtumour	1100 kg/m^3	Absorption coefficient of tumour, μa	0.06/cm
Specific heat of (tissue/tumour), Ct	4200 J/kgK	Scattering coefficient of tumour, μs’	3.25/cm
Thermal conductivity of tumour, Ktumour	0.55 W/mK	Metabolic heat of tissue, Qm_tissue	1091 W/m^3
Thermal conductivity of tissue, Ktissue	0.5 W/mK	Metabolic heat of tumour, Qm_tumour	65,400 W/m^3

Since the optical characteristics of a nanoparticle-embedded tumour are a strong function of wavelength, the spectral characteristics of the irradiation must match the optical response of the GNRs. A collimated, near-infrared radiation with a beam diameter of 20 mm (corresponding to the tumour diameter) was selected to uniformly irradiate the tumour surface. The spatial intensity of irradiation was considered with ‘top hat’ or ‘flat’ profile. The spectral emission was taken to be equivalent to a laser with peak irradiance at 796 nm and spectral width of 5 nm. The selected spectral intensity was varied within the range of 0.2–0.3 W cm⁻²nm⁻¹ and the corresponding integrated intensity in this spectral band was 1–1.5 W/cm². This intensity value is optimal for the volume fraction (0.001%) of GNR under consideration [2,6].

For an absorption-dominated medium, the irradiation absorption can be obtained using Beer’s law, as shown in Equation 1(1a) . Equation 1(1a) gives accurate results for the condition where NC_scaΔZ ≪ 1 [40]. Where, N is the number of nanoparticles per unit volume, C_sca is the scattering cross-section of GNR and ΔZ is the discretised thickness or path length. This condition is satisfied for the range of parameters considered in the present study. (1a) (1b) (2) where, represents spectral intensity of incident radiation and denotes spectral intensity attenuated through each layer of thickness ΔZ (as shown in Figure 1). The symbols μ_abs and μ_sca denote the absorption and scattering coefficients, respectively. Q_abs denotes the irradiation absorbed within the tumour. Equation 1(1a) was discretised as a function of wavelength as well as space to obtain the irradiation absorption in each cell of the tumour. The spectral region was divided into wavelength intervals of 1 nm to accurately capture the wavelength-dependent optical absorption.

Thermal damage within the nanoparticle-embedded tumour

Thermal damage to a tissue is a function of temperature and time [41–43]. There are two commonly used models to assess the thermal effects for a tissue. These are (1) a thermal damage (Ω) parameter based on the Arrhenius equation and (2) a thermal dose or cumulative equivalent minutes (CEM). The Arrhenius method, (1), provides a better estimation at higher temperatures, above 48 °C [43]. In our study, thermal damage is evaluated based on the Arrhenius equation. As per the Arrhenius equation, thermal damage over time (duration of exposure, τ) is given by Equation 3(3) [43]. (3) where, Ω, is the thermal damage parameter and it represents the fraction of damaged cells through 1−exp^−Ω. When Ω = 1 it signifies that the 64% of the cells are damaged, whereas a value of Ω = 4.6 represents 99.6% cell damage. In Equation 3(3) , the symbol A is a frequency factor and E is the activation energy; collectively these are termed the Arrhenius parameters. R_g is the gas constant, T is the temperature of the tissue and C represents the concentration of cells. The parameters E and A are selected based on tissue type [41]. The Arrhenius parameters considered in this study are mentioned in Table 4. Since temperature varies with time, Equation 3(3) was discretised in time to evaluate the thermal damage.

Table 4. Arrhenius parameters considered in this study.

Parameters	Frequency factor, A (s^−1)	Activation energy, E (J/mol)
Vascular stasis	1.98 × 10^106	6.67 × 10^5
Thermal damage	3.1 × 10^98	6.03 × 10^5

It is well known that as tissue is heated, the blood perfusion rate increases initially and then decreases due to damage to the vasculature. At a certain stage blood perfusion stops completely due to vasculature failure. This phenomenon can be accounted for while evaluating the thermal damage through a parameter termed the ‘degree of stasis’ [21,22]. The degree of stasis or vascular stasis (Θ) represents the damage to the tumour vasculature and is given by Equation 4(4) . (4)

For evaluation of the vascular stasis, the values E and A (given in Table 4) are different than those used for evaluating the thermal damage [22]. In our study, the blood perfusion rate (w_b) was varied as a function of the degree of stasis (Θ) through the use of a set of equations given by Equation 5(5a) (determined experimentally) [22]. In Equation 5(5a) , w_b0 is the initial blood perfusion rate at time t = 0. During therapy, the blood perfusion rate was varied as a function of time through calculation of vascular stasis at each time interval. (5a) (5b) (5c) (5d)

The overall spatio-temporal thermal damage was then evaluated based on the temperature obtained by solving the Pennes bioheat equation for a two-dimensional cylindrical geometry as given by Equation 6(6) . Pennes’ bioheat model is extensively used for these types of heat transfer studies [44,45]. (6) where, T(r,z,t) is the spatio-temporal temperature. T_c denotes a core body temperature of 37 °C. Q_abs denotes the irradiation absorption in the GNR-embedded tumour (evaluated using Equation 2(2) ). Q_m denotes the metabolic heat generation rate. w_b denotes the blood perfusion. The present study uses Pennes’ bioheat model for evaluating the temperatures. Pennes’ model does not account for the discrete nature of vasculature. Future studies considering this (based on CT data, for example) may be useful for this evolving research area. There are other methods (e.g. the dynamic mode decomposition method) for simulation of the ablation treatment and these successfully employed an extended version of Pennes’ bioheat model [46]. In Equation 6(6) , the blood perfusion term accounts for different perfusion conditions to evaluate its effect on the attained temperature and thus the thermal damage during treatment. The meanings of the other symbols in Equation 6(6) and their respective values are given in Table 3. 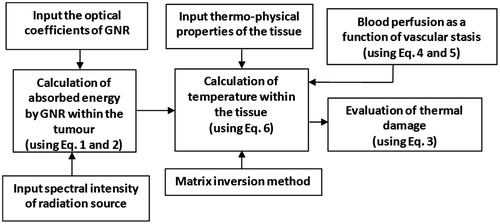Equation 6(6) was discretised using the finite difference implicit scheme. The nodal equations were generated by applying an energy balance for each nodal region [47]. Unknown temperatures were evaluated through the matrix inversion method implemented in MATLAB. An ambient natural convection boundary (10 W/cm²K, 25 °C) was considered at the top surface and a constant temperature condition of 37 °C was assumed at the other boundaries. A temperature of 35 °C was set as the initial condition for evaluating the spatio-temporal temperature field. The physical domain was discretised to radial and axial elements totalling to 81 × 41, respectively. For higher elements (101 × 51), the grid dependency of the results obtained was less than 0.1 °C. So a grid size of 81 × 41 was selected for evaluating the results. It is well known that a temperature of ∼50–60 °C is sufficient to thermally damage tissue [48]. The thermal damage parameter (Ω) was restricted to 4.6 (corresponding to 99.6% cell damage) because further increasing this parameter has little significance [20,43]. Figure 2 summarises the steps followed for evaluating the influence of blood perfusion on thermal damage.

Figure 2. Schematic representing the algorithm/steps followed in this study.

The numerical model developed was validated through comparison with published studies [1,2] as detailed in our earlier work [6].

Results and discussion

The spatio-temporal thermal ablation temperature and thermal damage evaluated for different cases of perfusion rates are presented and discussed in this section. At the end of this section we also highlight the temporal perfusion dynamics for the defined (ideal) therapeutic parameters.

Homogeneously perfused tumour

The temperatures as well as thermal damage (Ω) were evaluated considering the perfusion values (as listed in Table 1) for the conditions of constant blood perfusion and for variable perfusion (e.g. temporal variation based on the vascular stasis). The blood perfusion rate within the tumour was assumed homogeneous for obtaining the following results.

Low perfusion (almost equal perfusion within tumour and tissue)

For the low perfusion rates within the tumour and the surrounding healthy tissue, Figure 3(A) and (B) show the contours of the evaluated ablation temperature and the spatial profile of thermal damage during nanoparticle-assisted thermal therapy. Propagation of the thermal damage zone during irradiation is shown in Figure 3(C).

Figure 3. (A) Contour plot for thermal ablation temperature, (B) spatial profile of the thermal damage, at the end of irradiation duration of 105 s. (c) Contours for thermal damage zone (Ω = 4.6) at various time instants during irradiation. Irradiation intensity is 1 W/cm² for 105 s. GNR volume fraction is 0.001%. Perfusion data is as per Table 1 for the case of low perfusion. Constant blood perfusion is assumed (i.e. not varying with time).

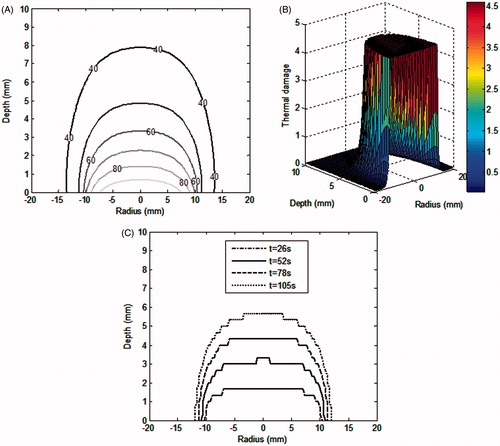
It can be seen from Figure 3(A) that the desired thermal ablation temperature is attained within the tumour region. The corresponding thermal damage zone, as shown in Figure 3(B), covers the tumour region. Figure 3(C) shows that with irradiation, the thermal damage zone propagates towards the deeper tumour region. At higher depths, the thermal damage zone narrows down along radial direction. This is due to the fact that during therapy, the blood perfusion at the tumour–healthy tissue boundary increases resulting in higher heat loss and hence lowers the ablation temperatures in this region.

Moderate perfusion

The temperatures as well as thermal damage were also evaluated considering higher perfusion values within the tumour as compared to surrounding healthy tissue. The thermal damage zone (Ω = 4.6) for the three different perfusion cases (as mentioned in Table 1) are collectively shown in Figure 4. Figure 4(A) and (B) show the results for constant perfusion and for variable perfusion (temporal variation as a function of vascular stasis), respectively.

Figure 4. Contours of thermal damage (Ω = 4.6) for three different blood perfusion values considering (A) constant blood perfusion i.e. not varying with time, (B) blood perfusion varying with vascular stasis. Irradiation intensity is 1 W/cm² for 105 s. GNR volume fraction is 0.001%. Perfusion rates are as per Table 1.

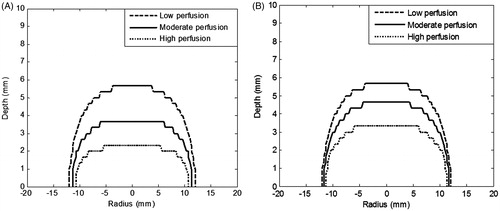
It can be seen from Figure 4(A) and (B) that for the ‘low perfusion case’, the spatial extent of thermal damage was not influenced by incorporating the vascular stasis-based variable perfusion. For these perfusion rates, the calculations showed that the temperature obtained at 5 mm depth within the tumour, T(0,5) was the same (49.2 °C) as in the constant and vascular stasis-based perfusion cases. Also, the surface temperatures were not significantly altered. So for the low perfusion rates it may not be necessary to incorporate a temporal variation of perfusion. It is to be noted that the therapy duration is quite short (∼2 min as opposed to 30–120 min in the case of conventional hyperthermia). So, for low perfusion rates, shorter therapeutic duration does not allow a significant loss of thermal energy due to blood flow (time scales of the order of 1 min). On the contrary, one study showed that blood flow may play important role in the shorter time scales of ∼8 s for ultrasonic lesion formation [49]. While this finding is not supported by our model (for low perfusion rates), more insight on this may be obtained through future studies considering the discrete nature of the vasculature.

For the moderate perfusion case, e.g. comparing Figure 4(A) and (B), it can be seen that the thermal damage spreads by 0.9 mm to a depth of 4.6 mm. Overall increase in the thermal damage zone is 25%. This means that vascular stasis aids the penetration of thermal damage to the deeper tumour region. So for moderate perfusion rates, there is a need to incorporate temporal variation of blood perfusion to get exact estimates of the thermal damage zone. But still the thermal damage does not cover the full depth of the tumour, so the tumour needs to be irradiated for a longer duration.

High perfusion

In this section, high perfusion rates (matching the highest reported values in literature) were assumed for both the tumour and surrounding healthy tissue. The perfusion rate in healthy tissue is one order of magnitude higher than that assumed in the Moderate perfusion section above. Using these high perfusion rates (as mentioned in Table 1), the thermal damage was evaluated for an irradiation duration of 105 s. The evaluated thermal damage zone for this case is included in Figure 4.

Comparing Figure 4(A) and (B), it can be seen that for the high perfusion case, the incorporation of the variable perfusion extends the thermal damage zone by 1 mm, i.e. penetration of thermal damage down to a 3.3 mm depth of tumour. In this case the thermal damage zone would be under-predicted by 52% if we consider a constant perfusion rate during the therapy. This is due to the fact that vascular stasis shuts off blood flow in the region and subsequently there is no heat loss due to blood flow. Overall, for moderate and high perfusion cases the thermal damage was extended to a depth of 4.6 mm and 3.3 mm, respectively. This shows that temporal variation in perfusion needs to be considered for moderate and high perfusion. But for fixed irradiation parameters and nanoparticle volume fractions, higher perfusion rates still result in significant heat loss from the tumour, and thus incomplete damage. So for moderate and high perfusion rates, the tumour needs to be irradiated for a longer duration to extend the thermal damage into the deeper tumour region (to a depth of 5 mm). Upon increasing the irradiation duration (of a fixed intensity) to 150 s (an increase of ∼1.5×), the thermal damage zones attained are shown in Figure 5. The irradiation duration was selected to avoid a tumour surface temperature of more than 100 °C.

Figure 5. Contours of thermal damage zone (Ω = 4.6) within the homogeneously perfused tumour and tissue considering (A) constant blood perfusion, i.e. not varying with time, (B) blood perfusion as a function of vascular stasis. Irradiation intensity of 1 W/cm² for 150 s. GNR volume fraction is 0.001%. Perfusion rates are assumed as per Table 1.

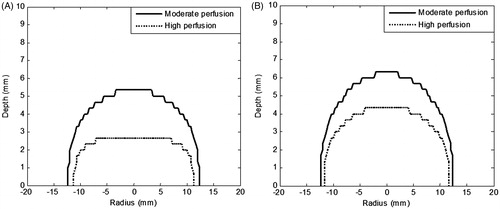
It can be seen from Figure 5(B) that for moderate perfusion the thermal damage zone covers the entire tumour depth, whereas for high perfusion the thermal damage (Ω = 4.6) was still restricted to a 4.2 mm depth which is not enough to completely damage the tumour. So there is a need to optimise for higher irradiation intensity for this case.

Importantly, the results discussed show marked variation in the thermal damage for the constant versus varying perfusion (temporal variation). The results also indicate that (for the high perfusion case) higher irradiation duration of 150 s (for a fixed irradiation intensity of 1 W/cm²) does not lead to the desired spread of thermal damage to the tumour depth of 5 mm.

Heterogeneously perfused tumour (spatial variation of blood perfusion within tumour)

For the results discussed in the previous subsection, a homogenous blood perfusion rate was assumed within the tumour. As mentioned earlier, there is a spatial variation of the perfusion in large tumours. So, considering the perfusion data in Table 2, the temperature field and thermal damage were evaluated for a moderately and highly perfused tumour (with and without necrotic core). In the present numerical model we have assumed a uniform concentration of GNRs within the whole tumour. The presence/absence of nanoparticles in the core depends on the method opted for delivering the nanoparticles to the tumour. Nanoparticles delivered through an intravenous method tend to reside around the vascularised region of the tumour, whereas nanoparticles delivered through skilled local/interstitial injection can potentially deliver a uniform concentration into the injected area. This distribution role of nanoparticle concentrations was highlighted in our earlier study [23]. The temperature contours attained for a highly perfused tumour with a necrotic core are shown in Figure 6. Figure 6(A) and (B) show the results for irradiation duration of 105 s and 150 s, respectively. The corresponding results for thermal damage are shown in Figure 7. It was found that upon increasing the irradiation duration to 150 s, the surface temperature T(0,0) just reached 100 °C. Thus, the irradiation duration was restricted to 150 s.

Figure 6. Contour plot of temperature for highly perfused heterogeneous tumour with necrotic core. Irradiation intensity is 1 W/cm² for duration of (A) 105 s, and (B) 150 s. GNR volume fraction is 0.001%. Vascular stasis-based perfusion variation is assumed . Perfusion data is for highly perfused tumour as per Table 2.

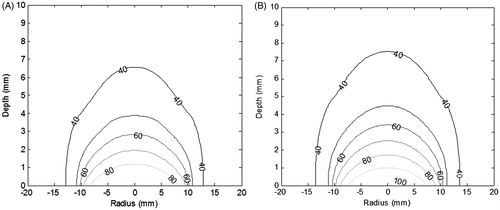
Figure 7. Contours of thermal damage zone (Ω = 4.6) for a heterogeneously perfused tumour for irradiation duration of (A) 105 s, and (B) 150 s. Irradiation intensity is 1 W/cm² and GNR volume fraction is 0.001%. The blood perfusion rate was varied as a function of vascular stasis. Perfusion rates are as per Table 2.

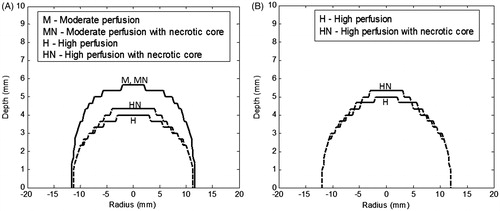
Figure 6(A) and (B) show that with higher irradiation duration there is a slight gain in temperature (at a depth of 5 mm). It can be seen that the 50 °C temperature contour is extended to a depth of 4.3 mm. But as seen from Figure 7, there is substantial gain in the thermal damage zone due to longer exposure of the tumour to the temperatures (time is also a factor for thermal damage). Figure 7(B) shows that by increasing the irradiation duration to 150 s for a highly perfused heterogeneous tumour, the thermal damage zone spreads well to ∼5-mm depth.

By comparing the temperature contours for a moderately perfused heterogeneous tumour (Figure 7A) with the homogeneously perfused tumour (low perfusion case, Figure 4(B), where perfusions are of the same order of magnitude), the spatial variation of the perfusion rate within the tumour did not significantly influence the thermal damage along the depth as well as the radius. So incorporating the perfusion heterogeneity for such perfusion rates does not alter the thermal damage zone. Also, it can be seen from Figure 7(A) that for a moderately perfused tumour there is nil variation in thermal damage upon incorporating perfusion with and without necrotic core.

Figure 7 shows that the spatial heterogeneity of perfusion plays an important role for high perfusion rates. It is inferred from Figure 7(A) and (B) that for a highly perfused tumour with a necrotic core the thermal damage penetrates deeper due to the absence of perfusion at the tumour core, but that it drops sharply at the tumour periphery.

Therapeutic parameters versus perfusion dynamics

The results discussed above imply that the spatio-temporal perfusion dynamics (during the therapy) influence the rate of thermal energy stored within the tumour as well as the rate at which the heat transfer occurs to the blood (Q_blood). So, for a given tumour tissue perfusion dataset, the external input power should overcome the Q_blood as per perfusion dynamics. Only then can ablation of the whole tumour be achieved. Figure 8(A) and (B) show the temporal variation in the thermal energy storage and heat loss rates at various depths within the tumour (considering vascular stasis-based perfusion). These are plotted for moderately and highly perfused, heterogeneous, non-necrotic tumours (data as per Table 2), respectively.

Figure 8. Temporal variation in the heat stored within the heterogeneously perfused tumour and heat lost due to blood perfusion for (A) moderately perfused tumour, (B) highly perfused tumour. Irradiation intensity is 1 W/cm² for irradiation duration of 105 s and GNR volume fraction is 0.001%. Vascular stasis-based perfusion is assumed. Perfusion rates are considered as per Table 2. Please note the different y-scale magnitude for ‘heat loss due to blood’ plots.

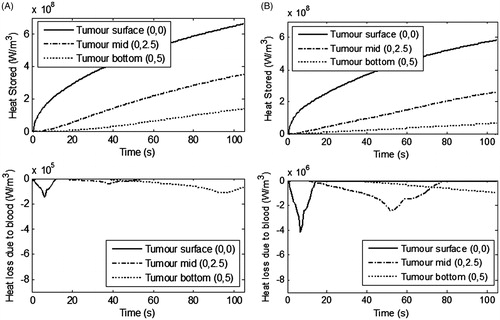
Figure 8(A) shows that for a moderately perfused tumour the thermal energy stored within the tumour is sufficient for thermal damage. Heat transfer to the blood flow is minimal and thus the desired thermal damage could be attained within the tumour for an irradiation duration of 105 s, but for the highly perfused tumour (as seen from Figure 8B), the peak heat loss due to blood flow is almost 28 times higher at the tumour surface. It can also be seen that at the mid region of the tumour the heat loss due to blood is higher and continues for longer time-scales compared to that for the moderately perfused tumour. Perfusion ceases at some time point due to complete damage of the blood vessels in this region. This considerable heat loss due to blood flow, for the same irradiation parameters (1 W/cm² for 105 s), restricts the thermal damage to a partial region of highly perfused tumour. A greater spatial extent of thermal damage can be achieved by either increasing the irradiation intensity, duration, or volume fraction of the nanoparticles. A recent study showed that for nanoparticle volume fractions higher than 0.001%, there is no significant increase in penetration of therapy deeper within the tumour [23]. So keeping a fixed dose of nanoparticles, the other parameters, i.e. irradiation intensity and duration, can be enhanced to attain the desired thermal damage. For the present case, higher irradiation duration of 150 s is used to increase the depth of thermal damage in the tumour.

For the therapeutic parameters considered here, the temporal changes in the ‘degree of stasis’ and blood perfusion rate were also highlighted for the moderately and highly perfused tumours. These plots are shown in Figure 9.

Figure 9. Temporal variation in the degree of vascular stasis and corresponding blood perfusion within the heterogeneously perfused tumour for (A) moderately perfused tumour, (B) highly perfused tumour. Irradiation intensity is 1 W/cm² for irradiation duration of 105 s and GNR volume fraction is 0.001%. Perfusion rates are as per Table 2. Please note the different y-scale magnitude for ‘blood perfusion’ plots.

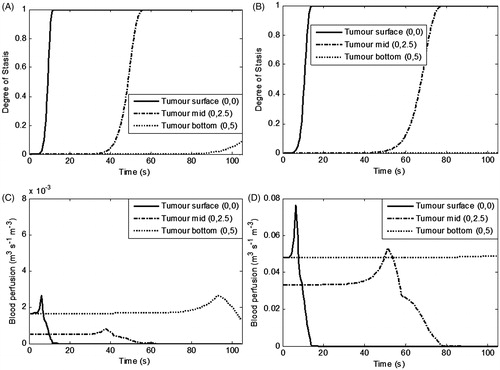
It can be seen from Figure 9 that at the tumour surface stasis occurs almost instantaneously, whereas at the tumour mid region stasis duration is influenced by the blood perfusion rate. Figure 9(B) shows that at the mid region for the highly perfused tumour tissue, the stasis completed at longer time scales (30 s) as compared to the moderate perfusion region (22 s). This is expected considering that during therapy the nanoparticles at the surface absorb a major part of the irradiation intensity. Stasis at the tumour bottom is negligible for a highly perfused tumour because, as discussed above, for 105 s irradiation, thermal ablation conditions are not attained in this region.

Regarding the corresponding blood perfusion variation, it can be seen from Figure 9 that at the tumour surface the blood perfusion rises sharply (1.5 and 1.7 times for moderately and highly perfused tumours respectively) and then drops to zero due to complete vascular stasis. Similarly, at the mid region of the tumour, there is a rise and drop in the perfusion, but this occurs at longer time scales. For the moderately perfused tumour, at the bottom region, perfusion rises due to a rise in the temperature in this region. But for the highly perfused tumour (bottom region), there is no change in the perfusion rate because the irradiation duration of 105 s was not enough to attain thermal damage at a 5-mm tumour depth. This is the why the irradiation duration was enhanced to 150 s (Figure 7B), which can provide the desired thermal damage zone for the highly perfused heterogeneous tumour. For the tumour size and perfusion conditions under consideration, the ideal therapeutic parameters were found to be irradiation intensity of 1 W/cm², and irradiation duration of 105–150 s for a nanoparticle volume fraction of 0.001%.

During hyperthermia and thermal ablation, the systemic temperature may increase. The magnitude of this increase depends on the treatment volume to which the energy is applied and on the methods to cool the patient [50]. It has been reported that for regional hyperthermia, a modest increase in the systemic temperature could counteract the increased cooling by localised blood perfusion, depending on the relative time scales [51]. However, systematic temperature increase would take several minutes to 1 h, which is unlikely to affect nanoparticle-assisted thermal therapy which takes in the order of ∼2 min. This issue may be investigated in detail in future studies.

Conclusions

In this study the role of the variability in blood perfusion for tumours and the surrounding healthy tissue was investigated during nanoparticle-assisted thermal therapy. Spatio-temporal variability of blood perfusion for various perfusion conditions was considered and the corresponding thermal damage zones were evaluated to understand the influence of blood perfusion.

The results show that for low perfusion rates the temporal variation in blood perfusion (during a therapy duration of ∼2 min) does not critically influence thermal damage. In the case of moderately and highly perfused tumours a temporal variation in the blood perfusion rate extends the thermal damage zone by 25–52% compared to the constant perfusion rate. Regarding the tumour perfusion heterogeneity (necrotic versus non-necrotic core), the spatial variation of the perfusion within a moderately perfused tumour does not alter the thermal damage zone. For highly perfused heterogeneous tumours, however, the necrotic core enables the extent of the thermal damage zone to reach deeper into the tumour region. For the tumour size and perfusion conditions considered in this study, the ideal therapeutic parameters were found to be an irradiation intensity of 1 W/cm² for a duration of 105–150 s with a uniform nanoparticle volume fraction of 0.001% within the tumour.

In conclusion, for low perfusion rates nanoparticle-assisted thermal therapy is relatively insensitive to temporal variation in the perfusion rate during therapy (due to the shorter therapeutic duration of ∼2 min as compared to the 30–120 min of conventional hyperthermia). For moderately and highly perfused tumours, the assumption of constant perfusion (during therapy) under-predicts the thermal damage zone. So relying on constant perfusion-based thermal damage results can lead to significant damage of surrounding healthy tissue due to under-prediction of the thermal damage zone. For effective therapy, the therapeutic parameters need to be selected based on perfusion dynamics to overcome the heat loss due to blood perfusion.

Declaration of interest

S.S. and H.T. wish to acknowledge the support provided by the School of Mechanical, Materials and Energy Engineering at the Indian Institute of Technology, Ropar. S.S. also acknowledges the support of CSIR - Central Scientific Instruments Organisation, Chandigarh. R.A.T. acknowledges the University of New South Wales Early Career Researcher (ECR) faculty scheme and the School of Mechanical and Manufacturing Engineering (MECH) seed research funding scheme for support. The authors alone are responsible for the content and writing of the paper.