Dose or ‘LET’ painting – What is optimal in particle therapy of hypoxic tumors?

ABSTRACT

Background. Dose painting is a concept that may increase the tumor control probability (TCP). In particle therapy of hypoxic tumors, it may also be beneficial to redistribute the linear energy transfer (LET) so that the oxygen effect is minimized; so-called LET painting. The purpose of the present study was to use TCP estimates for comparing dose and LET painting of hypoxic tumors.

Material and methods. Protons, lithium ions and carbon ions were considered. Tumor images tentatively depicting hypoxia were used as input. Optimal dose prescription maps were obtained by optimizing TCP under dose and/or LET redistribution. TCPs were compared to those resulting from conventional particle therapy with no dose or LET painting. The therapeutic gain at a given iso-effect was calculated. Treatment adaptation during therapy in response to changes in the spatial hypoxia distribution was also considered.

Results. Both dose and LET painting gave higher TCPs compared to conventional particle therapy, irrespective of particle type. The therapeutic gain from LET painting, dose painting and combined dose+ LET painting was 1.09/1.43/1.45, 1.24/1.32/1.37 and 1.16/1.23/1.28 for protons, lithium ions and carbon ions, respectively. The importance of treatment adaptation was less pronounced for particles heavier than protons.

Conclusion. Dose painting results in higher TCP than LET painting, in particular for protons. For heavier ions, LET painting may also give an enhanced tumor effect compared to conventional particle therapy. Combined dose+ LET painting may only give a marginally increased effect compared to dose painting only. Adaptive carbon ion dose painting seems to be of less importance.

Tumor hypoxia is a known contributor to radioresistance and is associated with reduced disease-free and overall survival after radiation therapy for many solid tumors [1]. Strategies to overcome hypoxia-induced radioresistance have been devised [2,3], and a meta-analysis have shown a significant benefit of hypoxia modification during radiotherapy of squamous cell carcinoma of the head and neck [4]. Modeling studies also predict a substantial benefit from selectively increasing the radiation dose to hypoxic subvolumes within the tumor [5–7]. With intensity-modulated radiation therapy (IMRT) and related techniques, dose distributions conforming to these subvolumes can be created, so-called hypoxia dose painting [5–8]. Recent advances in functional and molecular imaging are making the identification of such hypoxic subvolumes possible [9].

To realize the full potential of hypoxia dose painting with low linear energy transfer (LET) radiation, such as photons, poses several challenges. Among others, the oxygen enhancement ratio (OER) tells us that a factor three higher dose is required to eradicate hypoxic cells compared to fully oxygenated cells [10]. This calls for very steep dose gradients between hypoxic and normoxic subvolumes within the tumor, as well as between hypoxic tumor subvolumes and adjacent normal tissues [6]. Furthermore, therapeutic photon beams put physical limitations on the steepness of the intratumoral dose gradients that can be achieved [11]. Moreover, the required high dose gradients can also make the resulting treatment plans susceptible to both set up errors and variations in hypoxia during therapy [6,12]. In contrast, for intermediate to high LET particles, such as protons and carbon ions, OER decreases as LET increases [10]. Furthermore, the depth dose curves of heavy ions are markedly different to those of photons, with a substantial part of the total energy deposition taking place over the narrow Bragg peak [13]. On the one hand, this provides better dose conformation than for photons and steeper dose gradients can be achieved. On the other hand, very steep dose gradients for hypoxia dose painting may not be required in particle therapy due to lower OER. Thus, particles have attractive radiobiological and physical properties that potentially could alleviate some of the problems posed by hypoxia dose painting with photons.

In addition to dose painting, particle therapy may also offer the possibility of modulating the LET over the tumor; so-called LET painting [14–18]. As LET increases (and OER decreases) with decreasing particle energy, tumor cell kill will be maximized if LET can be redistributed according to the spatial hypoxia profile. In others words, it would be beneficial if the high-LET Bragg peaks can mainly be co-localized with hypoxic regions, while the Bragg plateau of lower LET coincides with normoxic regions. Still, it is not known whether LET painting can give similar or higher tumor control compared to dose painting.

The purpose of the present work was to investigate the potential benefit of hypoxia dose and LET painting with particles of intermediate to high LET and to compare these results to those for low LET radiation. Semi-empirical modeling of the different painting strategies was employed using the linear quadratic cell survival formalism. It is shown that both dose and LET painting may give higher tumor control levels compared to conventional treatment, but that the therapeutic gain varies with the type of particle used.

Material and methods

Concept

The aim of the current work is to estimate the tumor effect from dose and/or LET painting for protons , lithium ions and carbon ions . This requires a tumor model where the radiosensitivity and the impact of oxygen concentration is given voxel by voxel. A canine hypoxic tumor model established earlier [6] was employed. The tumor model is based on dynamic contrast enhanced magnetic resonance (DCE-MR) images, where the spatial contrast enhancement pattern was transformed to a voxelwise pO₂ distribution. The images have a voxel resolution of 0.7 × 0.7 × 5 mm³. Image series obtained prior to each of 16 delivered radiotherapy fractions were available, which was used to study adaptive strategies (see below).

For dose and LET painting, it is assumed that doses and LET values can be perfectly distributed voxel-by-voxel in the tumor, as described in the procedures below. This work does not address dose planning optimization or dose delivery, and the doses and LETs given may thus be regarded as a prescription basis for further particle therapy dose planning. The estimated tumor control probabilities (TCPs) (see below) thus reflect a situation where the prescription basis can be perfectly reproduced in the tumor.

Tumor control probability (TCP)-modeling

In order to estimate the tumor effect resulting from dose and/or LET painting, a voxel based linear quadratic probability model was developed as follows [6,7]:

where N is the number of voxels in the tumor, ρi the initial cell density in voxel i, V_i the volume of voxel i, n the number of treatment fractions, d_ij the physical dose in voxel i at treatment fraction j, and α_ij and β_ij the linear and quadratic components of radiosensitivity in voxel i at treatment fraction j, respectively.

The dependence of TCP on oxygenation and LET was incorporated in the model through the expressions for the cellular radiosensitivities α and β as follows [19]:

Here, p is the partial pressure of oxygen (in mmHg) in the given region of the tumor and L the LET of the radiation in question (in keV/μm), while is K a parameter which controls the rate of change in OER with pO₂. a₁, a₂, a₃, a₄, b₁, and b₂ are parameters obtained by fitting the experimental data given in Wenzl and Wilkens [19]. This produces the following expression for the OER:

where p_a and p_h are the partial pressures of oxygen under aerobic and hypoxic conditions, respectively and S is the survival fraction.

LET painting

The intratumoral LET distribution for a spread-out Bragg peak (SOBP) was estimated as outlined in the following. The LET L is in this work given as the unrestricted LET, i.e. the stopping power. Concepts and quantities for radiation transport were taken from Attix [10]. Briefly, simplified particle transport through a one-dimensional (1D) voxelized tumor with voxel dimension Δ was considered, neglecting straggling, scattering and creation of secondary charged particles. Thus, the particle fluence Φ_E of a given energy bin E was assumed to be constant with depth up the corresponding particle range. The relative biological effectiveness (RBE)-weighted dose at a given depth is in this case

q is the charge of the particles and L is Bethe's stopping power for water. The particle track structure was neglected, and it could thus be assumed that RBE was determined by LET only [20]. RBE was estimated from α and β and their LET dependencies, assuming fully oxygenated conditions and a survival level of 10%, using Equation 2. It is stressed that the RBE-weighted dose is only used for generating SOBPs; the dose reported elsewhere is the physical dose (in units of Gy). The distal edge δ_max of the tumor was identified, giving a measure of the required maximum particle energy E(δ_max). At shallower depths, the particle energy, and thus the LET, was determined using a recursive formula. For the SOBP, a Bragg curve corresponding to E(δ_max) was first generated through the tumor. Then, another Bragg curve was generated up to depth δ=δ_max −Δ. In this case, the required fluence of the corresponding energy bin E(δ) was numerically adjusted in order to give the same biological dose as in the voxel at δ_max. Following this procedure up to the most shallow tumor voxel an RBE-weighted SOBP could be constructed with the resulting LET spectrum of primary ions contained in Φ_E.

The purpose of hypoxia LET painting is to maximize tumor cell kill by depositing particles with the highest LET in the most hypoxic tumor regions. In the current work, a full voxelwise pO₂ map of the tumor is available and such maximization may be achieved by assigning LET values from the SOBP LET spectrum to each voxel according to the pO₂. A rejection sampling technique was used to generate a list of LET values from the spectrum equaling the number of voxels. From this list, the highest LET value is assigned to the lowest pO₂ value while the lowest LET value is assigned to the highest pO₂ value and so forth. In this way, the LET spectrum originally giving a homogenous SOBP is now inhomogeneously redistributed. The LET redistribution is done under the assumption that the tumor dose is kept constant. If no LET painting is done in the modeling, the LET values are randomly distributed throughout the tumor. It is stressed that the simplified LET painting done in the current work assumes that the LET values from an SOBP LET spectrum can be perfectly redistributed, neglecting any issues regarding plan optimization and delivery.

Dose painting

The optimal dose distribution d_ij in voxel i at treatment fraction j yielding maximal TCP was calculated under the condition of constant integral tumor dose using the Lagrange multiplier method [6,7,21]:

This gives a set of non-linear equations on the form

Following Yang and Xing [21], subscript r refers to reference values required for solving the set of equations. α_r, β_r are set to the mean parameter value taken over tumor, while d_r is the mean fraction dose. The voxel clonogen density ρ is assumed to be constant over the tumor, but its r- and i subscripts are preserved for consistency. Furthermore, we make the following assumption:

This reduces Equation 6 to one that can be solved analytically for d_ij:

The dose redistribution, or dose painting, concept outlined can be achieved with or without LET painting, as the latter only modulates α and β in the current formalism. Thus, both LET, dose and combined LET and dose painting, was modeled.

Model input

From the pO₂ images, radiation sensitivities could be calculated from Equation 2, where the following parameters were used: a₁ = 0.44 Gy⁻¹, a₂ = 0.0088 μm (Gy keV)⁻¹, a₃ = 0.19 Gy⁻¹, a₄ = 0.0056 μm (Gy keV)⁻¹, b₁ = 0.19 Gy⁻¹, b₂ = 0.0069 Gy⁻¹. It is noted that the parameter values were derived by non-linear regression of the experimental OER-LET survival data summarized by Wenzl and Wilkens [19], but that our values differ from those published by Wenzl and Wilkens. The reasons for these discrepancies were not attempted to be solved in the current work, as our parameters gave reasonable OERs (see discussion). Furthermore, K was set to 3.0 mmHg. The cell density ρi was assumed constant and equal to 10⁷ cm^-3 over the tumor, and the reference cell density in Equation 8 was also set to this value. The reference dose in Equation 8 was set to the mean tumor dose. The total number of fractions in the TCP calculations was 16, corresponding to the number of fractions for which tumor oxygen images were available.

Analysis

The optimal dose distribution d_ij for dose painting based on the hypoxia images was determined for a given particle type using Equation 8. The optimal LET distribution was derived from Equation 4 and subsequent calculations. If not otherwise stated, the resulting TCP was calculated based on daily pO₂ images for the entire treatment, taking variations in radiosensitivities α_ij and β_ij during treatment into account. TCPs were compared to that from conventional particle therapy with a uniform dose distribution in the tumor.

The therapeutic gain was defined as the ratio between the mean tumor doses for conventional therapy and hypoxia painting at an iso-effect level of 50% TCP, emphasizing the potential reduction in tumor dose that can be achieved by painting. Here, conventional therapy is defined as particle therapy with the specified ion species giving a homogenous tumor dose. The effect of replanning, or biologic adaptation, during treatment in response to spatial changes in intratumoral oxygen distribution was also investigated. Here, the dose distribution based on the pretreatment images was used only for j–1 treatment fractions before replanning was performed and a new dose distribution d_ij was employed. Various strategies with different number of replanning sessions were evaluated, corresponding to replanning once half-way during treatment, replanning once per week and replanning before each treatment session. This corresponds to 1, 2, 4 and 16 treatment planning sessions. As before, the fraction specific distribution of radiosensitivities α_ij and β_ij was used for all treatment fractions in calculating the TCP. The effect of replanning was estimated by the therapeutic gain.

Results

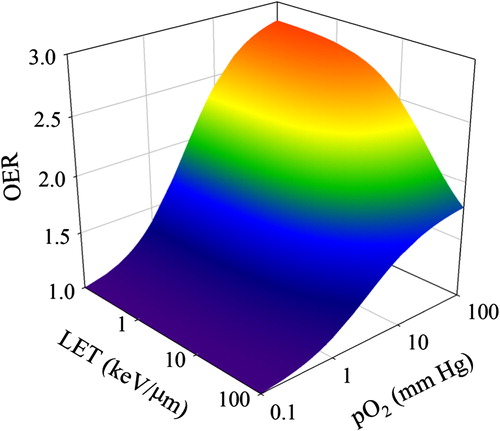
OER as a function of LET and partial oxygen pressure for the parameter values used in this study is shown in Figure 1. As expected, OER increases with increasing degree of oxygenation and decrease with increasing LET.

Figure 1. Oxygen enhancement ratio (OER) as a function of linear energy transfer (LET) and partial pressure of oxygen (pO₂), as appearing using the model parameters in the current work.

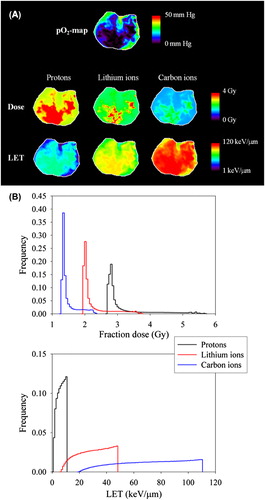
Figure 2A shows the optimal dose and LET maps for an iso-effect of 50% TCP at the first treatment fraction for the three ion species in question. As seen, high doses and high LET values are prescribed to voxels with low pO₂ (and thus high OER) in order to optimize the TCP. The full dose- and LET distributions are given in Figure 2B. The range of LET values was about 1–11 keV/μm, 6–48 keV/μm and 19–110 keV/μm for protons, lithium ions and carbon ions, respectively. For dose painting, the mean fraction dose giving an iso-effect of 50% TCP was 3.1, 2.2 and 1.5 Gy for protons, lithium ions and carbon ions, respectively. The difference between the maximum and minimum dose to the tumor, relative to the mean dose, was 0.92, 0.77 and 0.66, respectively.

Figure 2. (A) Map of the partial pressure of oxygen (pO₂) in a single slice of the tumor prior to the first treatment fraction (upper). Corresponding maps of the optimal dose and LET distribution are also given (middle and lower, respectively). The dose and LET range is indicated by the color bar with a linear and logarithmic scale, respectively. (B) Histograms of the full dose and LET distributions in the tumor in the case of dose- and LET painting, respectively.

TCP as a function of the mean tumor dose for conventional particle therapy, dose painting, LET painting and combined dose and LET painting is displayed in Figure 3. Here, full biological adaptation is assumed with a dose and/or LET prescription corresponding to each single treatment fraction. First, as the mean particle LET is increased, TCP curves become steeper and are progressively shifted towards lower mean dose values. Second, for a given particle species, TCP curves for conventional therapy is always found at the highest doses, indicating that this is the least favorable strategy. Third, TCP curves for dose painting are always found at doses lower than the curves for LET painting. Fourth, the TCP curves for combined dose and LET painting are consistently found at the lowest doses for a given particle energy, indicating that this is the most favorable strategy. These features are also reflected in the estimated therapeutic gain (Table I), where the highest therapeutic gain was found for combined dose and LET painting with protons, while the lowest corresponds to LET painting with protons. LET painting with lithium ions gives a higher therapeutic gain than LET painting with carbon ions.

Figure 3. Tumor control probability (TCP) as a function of mean tumor dose for the three ions species considered.Four strategies were considered: 1. combined dose and LET painting (DP, LP), 2. dose painting only (DP, no LP), 3. LET painting only (no DP, LP) and 4. conventional radiotherapy (no DP, no LP).

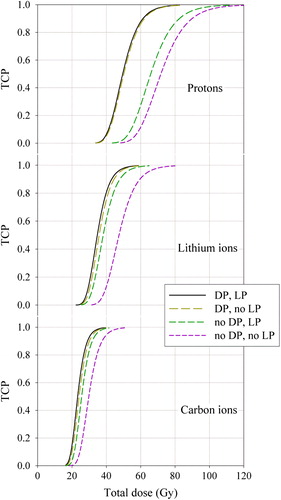
Table I. The therapeutic gain from dose-and/or LET painting, expressed in terms of the dose giving 50% TCP for a conventional treatment relative to the iso-effective dose for painting. In the case of painting, full adaption to day-to-day variations in tumor hypoxia were followed.

Ion species	No painting^a	LET only	Dose only	Dose + LET
Protons	1.00	1.09	1.43	1.45
Lithium ions	1.00	1.24	1.32	1.37
Carbon ions	1.00	1.16	1.23	1.28

^aNo painting corresponds to a conventional treatment with a homogeneous tumor dose, and gives by definition a therapeutic gain of unity.

The effect of replanning, i.e. treatment adaption, in response to changes in tumor hypoxia during treatment is also estimated by the therapeutic gain. As seen in Table II, increasing the number of planning sessions always gives an increase in therapeutic gain, but to a smaller degree for lithium ions and carbon ions. Also, just one planning session for painting (prior to the first treatment fraction) gives a considerable therapeutic gain for all ion species. The highest therapeutic gain was found for protons with daily adaptation to changes in hypoxia at each of the 16 sessions. The lowest was found for carbon ions with one planning session for painting, but here the therapeutic gain was still rather high (1.20).

Table II. The therapeutic gain from replanning of combined dose- and LET painting, expressed in terms of the dose giving 50% cure for a conventional treatment relative to the iso-effective dose for painting.

	Number of planning sessions
Ion species	0^a	1	2	4	16
Protons	1.00	1.24	1.38	1.43	1.45
Lithium ions	1.00	1.26	1.33	1.36	1.37
Carbon ions	1.00	1.20	1.25	1.27	1.28

^aZero sessions corresponds to a conventional treatment, i.e. no painting and homogeneous tumor dose, and gives by definition a therapeutic gain of unity.

Discussion

The present study demonstrates that hypoxia dose painting with particles of intermediate to high LET potentially can improve treatment outcome compared to conventional particle therapy employing a homogenous tumor dose. Hypoxia dose painting appears particularly attractive for protons, while dose painting with lithium ions or carbon ions gave somewhat lower therapeutic gains. Conversely, LET painting may also be beneficial, but the estimated clinical impact of this strategy was always smaller than for dose painting. Combined dose and LET painting gave the highest TCPs overall, but the increase in tumor effect was not substantial compared to dose painting only.

Normal tissues and their associated complication probabilities [22] were not explicitly included in the present work. For both low and high LET radiation, the presence of adjacent normal organs may modify the dose distribution that can safely be used in the tumor, particularly if a hypoxic region is localized towards the periphery of the tumor and in close proximity to a critical organ. Based on the potential for dose reduction with high LET dose painting, reduced probability of normal tissue complication is expected compared to photons. However, this should be verified in further studies.

The three different particle species were selected in the current work due to that protons and carbon ions are in clinical use and that lithium ions is of potential clinical interest [23–25]. Also, the three nuclides showed great differences in their LET spectra and optimized dose distributions. Protons have low to intermediate LET values, giving a high OER and low RBE, and thus result in high tumor dose gradients for optimal hypoxia dose painting. This was indicated by the high relative difference found between the maximum and minimum tumor dose for protons. However, if these dose painting prescription criteria can be met in the treatment planning system our results show that the therapeutic gain is the greatest for this ion species. In the case of LET painting, lithium ions gave the highest therapeutic gain. This is because the range of LET values that can be painted allows for greater differentiation in biological effect between the voxels, relative to a strategy where LET values are randomly distributed in the tumor. For carbon ions the differences in biological effect across the LET spectrum is not that great relative to the conventional strategy. Still, carbon ion LET painting requires 14% less dose (therapeutic gain 1.16) compared to conventional carbon ion therapy for the same tumor iso-effect, so LET painting may be clinically attractive. However, carbon ion dose painting reduced the integral tumor dose by 19% for the same iso-effect, indicating that this strategy is preferable over LET painting.

The parameters used in the present work to describe the dependence of OER on LET and pO₂ were derived from Wenzl and Wilkens [19]. Their approach gave a unified theory where the impact of LET and pO₂ could be modeled and further incorporated into the current TCP framework. Later, Scifoni et al. used similar considerations in calculating the OER [26], with the resulting LET-pO₂ dependence being similar to Figure 1 in the current work. Furthermore, Antonovic et al. [27] employed a LET-parameterized repairable–conditionally repairable damage cell survival model to arrive at OERs comparable to those obtained in the current study. Also, the results from the present work are in line with our previous modeling studies on low-LET dose painting with simpler modeling approaches [6], showing similar tumor control levels for dose painting. Therefore, the impact of LET and pO₂ on the intrinsic tumor radiosensitivity seems adequately taken into account in the present work.

LET painting was originally introduced by Bassler et al. [14], where the concept was explored by arranging carbon ion beams in different manners. Recently, this work was followed up in more detail, where carbon ions and oxygen ions were employed in treatment planning of a case of hypoxic oropharyngeal cancer [15]. LET painting with ‘ramped’ beams proved feasible, but the corresponding increase in TCP was not substantial for carbon ions, as opposed to the current work. The small impact of LET painting could possibly be due to that the applied doses were too low in order to observe a significant change in TCP. Still, Bassler et al. [15] could demonstrate a higher impact from LET painting with oxygen ions, in particular if an additional dose boost was delivered to the hypoxic region. The latter is in line with the current work, where combined LET and dose painting gave the highest therapeutic gain. LET painting has also been explored by other groups [16–18], but in these cases only protons were considered and hypoxia imaging was not employed. Yet, increased tumor RBE was demonstrated in spite of protons having low- to intermediate LET values. This is in accordance with the current study, where an increase in therapeutic gain (9%) from proton LET painting was found. Thus, together with published literature on the topic, the current work demonstrates that LET painting could be clinically attractive in particle therapy.

In the present modeling study, the practicality of planning and delivering the desired dose and LET distributions was not investigated. Clinical dose painting with photons is already a reality [28], and intensity-modulated particle therapy (IMPT) offers the same possibilities with respect to dose painting [29]. Still, to our knowledge, conditional LET optimization, required for LET painting, has not been incorporated in IMPT treatment planning systems. However, the particle treatment planning system TRiP has been extended to include OERs in the plan optimization, leading implicitly to LET painting [26]. Our work can potentially be used a prescription basis for dose/LET painting, where the optimal dose/LET maps can be imported into the IMPT optimizer. Still, more work is to be done before combined dose/LET painting can be fully realized with IMPT.

Biologically adapted dose painting has been advocated to take changes in tumor biology during the course of fractionated radiotherapy into account [28]. Biological adaptation to changes in tumor hypoxia was incorporated in the current work, as hypoxia images acquired prior to each of 16 radiotherapy sessions could be used to generate optimal dose and LET distributions. The therapeutic gain was found to increase with the number of dose/LET painting planning sessions for all ion species, in line with our previous study on low-LET dose painting [6]. The maximal therapeutic gain was found for protons with full biological adaptation, i.e. prescribing a new hypoxia plan at each treatment session. Carbon ions gave the lowest therapeutic gain following replanning, as could be expected due to their high RBE and low OER. However, in the case of replanning, a low therapeutic gain may in fact be an advantage, as treatment adaptation is costly and increases the complexity of the treatment. In that respect, dose and/or LET painting with carbon ions may be preferable.

There are limitations with the current work with respect to making firm conclusions on the impact of dose and LET painting. First, the longitudinal DCE-MR image series employed was for one tumor only, and the pO₂ image values have not been validated. Still, there is increasing evidence that DCE-MRI may produce images reflecting hypoxia [9]. Furthermore, a simplified method was used in the present work to calculate LET spectra in the tumor, but the LET values produced are comparable with other LET painting studies [14–18]. Also, nuclear fragmentation was not considered, which will lead to underestimated LET values in the case of carbon ions and deep seated tumors. Besides, the optimal LET and dose distributions obtained can most probably not be achieved in reality due to limitations in treatment planning optimization and in delivery of the prescribed plans. Thus, our estimated therapeutic gains are upper limits to what can be achieved clinically. Also, the tumor considered was large and highly hypoxic, and the therapeutic gain from dose and/or LET painting is thus expected to be lower for smaller and less hypoxic tumors. Furthermore, modeling studies are generally limited by the underlying theoretical assumptions and modeling parameters. Still, modeling is an attractive approach to explore novel strategies, and the current work presents a first step in assessing the impact of dose and LET painting.

In conclusion, dose and LET painting may increase the probability of eradicating hypoxic tumors, but the impact varies with the ion species employed and whether adaptation is performed. Still, further studies are needed, both with respect to improving dose and LET planning optimization tools and acquiring pre-clinical and clinical data that could support implementation of this concept.

Declaration of interest: The authors report no conflicts of interest. The authors alone are responsible for the content and writing of the paper.