Ultra-short Laser Pulse Generated by a Microring Resonator System for Cancer Cell Treatment

Abstract

A microring resonator (MRRs) system incorporated with a add/drop filter is proposed in which ultra-short single, multi-temporal, and spatial optical soliton pulses are simulated and used to kill abnormal cells, tumors, and cancer. Chaotic signals are generated by a bright soliton pulse within a nonlinear MRRs system. Gold nanoparticles and ultra-short femtosecond/picosecond laser pulses’ interaction holds great interest in laser nanomedicine. By using appropriate soliton input power and MRRs parameters, desired spatial and temporal signals can be generated over the spectrum. Results show that short temporal and spatial solitons pulse with FWHM = 712 fs and FWHM = 17.5 pm could be generated. The add/drop filter system is used to generate the high-capacity, ultra-short soliton pulses in the range of nanometer/second and picometer/second.

Keywords::

• Abnormal cells
• microring resonator
• gold nanoparticles
• laser-nanoparticle interaction

Introduction

Ultra-short laser pulse thermal-based killing of abnormal cells such as cancer cells using nanoparticles is becoming an interesting subject in nanophotonics and medical treatments (Pitsillides et al. 2003, Zharov et al. 2005, Letfullin et al. 2006). Thermal treatment using photo-absorbing generated heat from optical energy, which has many advantages compared to other treatment methodologies and cancer therapies, such as surgery and radiotherapy. A wide range of nanomaterials with strong optical absorption in the near-infrared (NIR), such as gold nanoparticle (Maltzahn 2009), nanoshells (Hirsch et al. 2003), or carbon nanotubes (Moon et al. 2009, Ghosh et al. 2009, Liu et al. 2011), can be used as photothermal. Laser energies of ultra-short pulses can be concentrated on small biological mass filled with metallic nanoparticles. Therefore, an ultra-short laser pulse shoots photons to the target, where it can be absorbed by free electrons within the particle and transferred to the lattice of subsystem, and finally to the surrounding medium. The knowledge of laser interactions with the nanoparticle requires specific models for each case, which depends upon the laser pulse duration. The model of dual-temperature for the ultra-short laser pulse mode is readily available (Wu et al. 1998, Chichkov et al. 1996).

Ultra-short pulses, specifically femtosecond and picosecond, are appropriate for medical treatment applications. Free electrons of nanoparticle materials, such as gold, absorb energy and transfer the thermal energy to the lattice. The delay time of electron cooling and lattice heating is in the order of femtoseconds and picoseconds, respectively (Inagamov et al. 2009, Krenzer et al. 2008). Two appropriate models, a one-temperature model (OTM) and two- temperature model (TTM), are well described. OTM is an operating uniform and suitable heating approximation for nanoparticle heating in the femtosecond and picosecond regimes. OTM provides an effective modeling method for further nanomedicine research and needs to be explored (Anderson and Parrish 1983). Nanoparticles in the blood and tumor are comparable to the water-surrounding medium case because the thermodynamic properties of those media are very close to each other. Fat has low-thermal characteristics compared to water. Therefore higher overheating of the gold nanoparticle can be seen at the same energy level.

The thermal equilibrium among the excited electron is within 100–175 femtoseconds. Electron cooling time due to the coupling to lattice is about 10 picoseconds. In the case of the OTM model, the heat flows from the nanoparticle into the surrounding medium and becomes noticeable after 200 picoseconds. Transferred energy from laser pulses to the medium is absorbed by the particles and cells. Gold nanoparticles can strongly absorb visible light, where it has a distinct absorption peak near 520 nm (Mie 1908).

This technique causes localized tumor damage without harmful effects on surrounding healthy tissue. Absorption of laser heat occurs at longer wavelengths for most biotissues with relatively fast treatment. Promising results are obtained with the use of gold nanoshells in the range of 800 nm using continuous laser radiation (O’Neal et al. 2004). To generate a spectrum of light over a broad range, an optical soliton pulse is recommended as a powerful laser pulse that can be used to generate chaotic filter characteristics while propagating within nonlinear microring resonators (MRRs) (Yupapin et al. 2008).

Using this technique, the capacity of the transmission data can be secured and increased when the chaotic packet switching is employed (Amiri et al. 2011). An in propose system of extremely short pulses in the range of pico- and femtosecond of soliton are used for abnormal cells oblation such as cancer or tumor. Ring resonators can be used to generate ultra-short pulses in the nonlinear regime (Yupapin et al. 2008). Two techniques are used to generate the soliton laser pulses. First, Pornsuwancharoen et al. (2008) showed that soliton pulses can be obtained using a pumped soliton pulse inside a ring system where large amplified signals are achieved. Second, a Gaussian soliton can be generated in a simple system arrangement. This application becomes an attractive tool in the area of nanomedicine applications. However, there are many research works which are reported in both theoretical and experimental works using a bright soliton pulse for soliton study (Purwins et al. 2010). In this work, a monochromatic laser source, such as a bright soliton pulse with central wavelength of 0.6 nm and 1550 µm, is used to generate a high capacity of ultra-short soliton signals within a nonlinear fiber ring resonator.

Numerical modeling

The schematic diagram of the proposed system is as shown in Figure 1. A soliton pulse with 20 ns pulse width and 500 mW peak power is input into the system. The suitable ring parameters are used; for instance, ring radii R1 = 10 µm, R2 = 5µm, and R3 = 4µm. In order to make the system associate with the practical device, the selected parameters of the system are fixed to l0 = 0.6 m and 1.55 m, n0 = 3.34 (InGaAsP/InP), Aeff = 0.50, 0.25 m² and 0.12 m² for different radii of microring resonators, respectively, a= 0.5 dBmm⁻¹, = 0.1. The coupling coefficient (kappa, κ) of the micro ring resonator ranged from 0.50 to 0.975 (Toulouse 2005).

Figure 1. Schematic diagram of a single and multiple ultra-short pulse generation for thermal-based killing of abnormal cells.

The bright soliton pulse is introduced into the proposed system, where the input optical field (E_in) of the bright soliton pulse is given by Giri et al. (2011),

A and z are the optical field amplitude and propagation distance, respectively. T is a soliton pulse propagation time in a frame moving at the group velocity, T = t − β₁ × z, is the dispersion length of the soliton pulse, where β₁ and β₂ are the coefficients of the linear and second order terms of Taylor expansion of the propagation constant. The frequency shift of the soliton is ω₀. This solution describes a pulse that keeps its temporal width invariance as it propagates, and thus is called a temporal and spatial soliton. When soliton peak intensity is , then T_o is known. For the soliton pulse in the micro ring device, a balance should be achieved between the dispersion length (L_D) and the nonlinear length , where ၵ = n₂ × k₀ is the length scale over which dispersive or nonlinear effects make the beam wider or narrower, hence L_D = L_NL. When light propagates within the nonlinear medium, the refractive index (n) of light within the medium is given by

where n₀ and n₂ are the linear and nonlinear refractive indexes, respectively. I and P are the optical intensity and optical power, respectively. The effective mode core area of the device is given by A_eff. For the MRR, the effective mode core areas ranges from 0.50 to 0.10 m² (Hiruma et al. 2012). When a soliton pulse is input and propagated within a micro ring resonator as shown in Figure 1, the resonant output is formed; thus, the normalized output of the light field is the ratio between the output and input fields E_out (t) and E_in (t) in each roundtrip, which can be expressed as

Here, κ is the coupling coefficient, and x = exp(−αL/2) represents a roundtrip loss coefficient, Φ₀ = kLn₀ and Φ_NL = kLn₂|E_in|² are the linear and nonlinear phase shifts, k = 2π/λ is the wave propagation number in a vacuum. L and α are a waveguide length and linear absorption coefficient, respectively. The optical outputs of a ring resonator add/drop filter system can be expressed by Eqs. (4) and (5) (Afroozeh et al. 2011).

where Et and Ed are the optical outputs of the through and drop ports, respectively, while the output power from the third ring of the MRR’s system is shown by E_outR3. The propagation constant is given by β = kneff, where the effective refractive index of the waveguide is represented by neff. The circumference of the add/drop ring is L = 2πR where R is the radius. When light travels in a MRR system at the point where the ring becomes close to the straight waveguide, only the resonance wavelength of light is coupled into the ring. By using the particular parameters of the add/drop device, the chaotic noise cancellation can be implemented. The coupling coefficients of the add/drop filter have been shown by κ₄ and κ₅. The micro ring resonator loss and the fractional coupler intensity loss are α = 0.5 dBmm⁻¹ and γ = 0.1, respectively, while the nonlinear refractive index can be neglected for an add/drop device (Filho et al. 2008).

Results and discussion

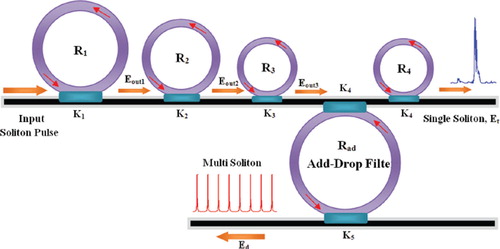
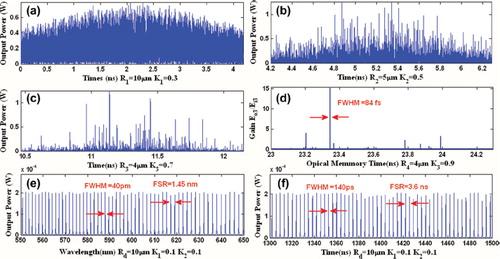
In operation, the large bandwidth within the micro ring device can be generated by a soliton pulse input into the nonlinear MRR as shown in Figure 1, where the ultra-short soliton pulses are generated. The nonlinear refractive index is n2 = 2.2 × 10−17 m²/W. The input signal is chopped (sliced) into the smaller signals spreading over the spectrum as shown in Figure 2, which shows that the large bandwidth is formed within the first ring device. The compress bandwidth with smaller group velocity is obtained within the ring R₂. The amplified gain is obtained within the R₃ microring device. The temporal soliton pulse can be formed by the constant gain condition, where a small group velocity is observed. The attenuation of the optical power within a microring device is required in order to keep the constant output gain. Similarly, the spatial soliton is obtained as shown in Figure 3. Figure 4 shows the generation of femtosecond pulse, where the radius of the rings has been selected to be R₁ = 17μm, R₂ = 13μm, R₃ = 7 μm, R₄ = 2 μm. The center wavelength of the input bright soliton is λ = 0.6μm. Spatial soliton pulse with FWHM of 0.34 nm can be generated at λ = 555 nm, as shown in Figure 5(d), whereas the steps of the filtering process are shown in Figures 5(a), (b), and (c). Figure 6 shows the results when temporal and spatial optical soliton pulses are localized within a microring device and add/drop filter system with 20,000 roundtrips, where optical an ultra-short temporal soliton of FWHM = 83 fs is generated. Here, the ring radii are R₁ = 10 μm, R₂ = 5μm, R₃ = 4 μm, R₄ = 4 μm and Rad = 200 μm with coupling coefficient of κ₁ = 0.3, κ₂ = 0.5, κ₃ = 0.7, κ₄ = 0.9, κ₅ = 0.1, and κ₆ = 0.1. Figure 7 shows the results of a localized ultra-short temporal optical soliton with 84 fs FWHM, where multi temporal optical soliton with FWHM = 140 ps and FSR = 3.6 ns are generated. The multi-spatial optical soliton have FWHM = 40 pm and FSR = 1.45 nm, where the ring radius of the add/drop filter system is Rad = 10μm and the central wavelength of the input bright soliton power has been selected to be λ = 0.6 μm.

Figure 2. Results obtained when the temporal soliton is localized within a microring device with 20,000 roundtrips: (a): chaotic signals from R₁; (b): chaotic signals from R₂; (c): trapping of temporal soliton; (d): trapped temporal soliton with FWHM of 4.8 ps.

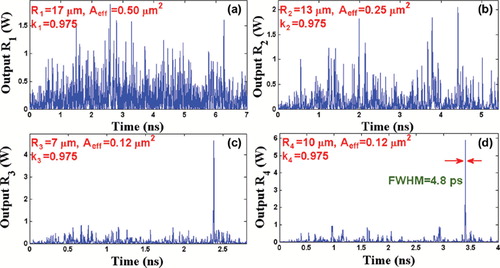
Figure 3. Results of trapping spatial soliton within a microring device with 20,000 roundtrips: (a): chaotic signals from R₁; (b): chaotic signals from R₂; (c): trapping of spatial soliton; (d): trapped spatial soliton with FWHM of 17.5 pm.

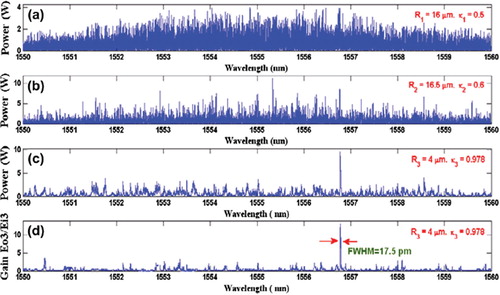
Figure 4. Results obtained when temporal soliton is localized within a microring device with 20,000 roundtrips: (a): chaotic signals from R₁; (b): chaotic signals from R₂; (c): trapping of temporal soliton; (d): trapped temporal soliton with FWHM of 712 fs.

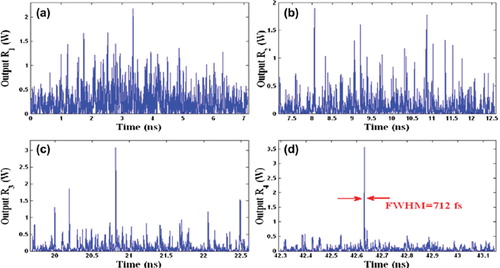
Figure 5. Results of trapping spatial soliton within a microring device with 20,000 roundtrips: (a): chaotic signal from R₁; (b): chaotic signals from R₂; (c): trapping of spatial soliton; (d): trapped spatial soliton with FWHM of 0.34 nm.

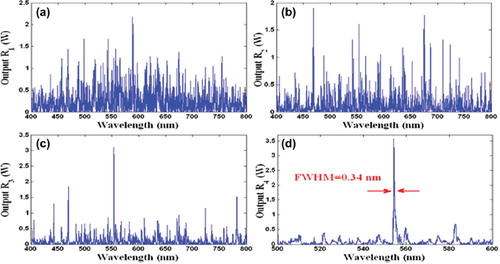
Figure 6. Results of temporal and spatial soliton generation: (a): chaotic signals from R₁; (b): chaotic signals from R₂; (c): filtering signals; (d): trapped temporal soliton with FWHM of 83 fs; (e): spatial soliton with FSR = 576 pm and FWHM = 19 pm; (f): temporal soliton with FSR = 502 ps and FWHM = 16.53 ps.

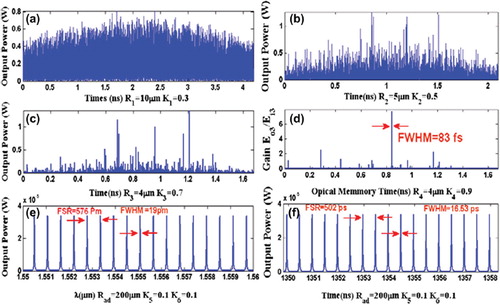
Figure 7. Results of temporal and spatial soliton generation: (a): chaotic signals from R₁; (b): chaotic signals from R₂; (c): filtering signals; (d): trapped temporal soliton with FWHM of 84 fs; (e): spatial soliton with FSR = 1.45 nm and FWHM = 40 pm; (f): temporal soliton with FSR = 3.6 ns and FWHM = 140 ps.

Precise ablation that is possible with pico- and femtosecond lasers makes them ideal candidates for high-precision surgery (Wieger et al. 2007). In the case of minimizing thermal effects in the area surrounding the abnormal target volume, femtosecond laser pulses can be used to selectively eliminate cellular components in individual cells, making them a powerful research tool. Interaction of an ultra-short laser pulse with gold nanoparticles transfer generated heat to abnormal cells such as tumor, cancer or plaque is shown in Figure 8 (Luo et al. 2008). Gold nanoparticles are the most promising candidates for photothermolysis since they are strong absorbers, photostable, and have adjustable optical properties. The gold nanoparticles in the size range of 2–250 nm form a cluster around a target molecule and are excited with a short laser pulse, act as a heat source, and generate an intracellular photothermal vapor bubble. Effects of the laser-nanoparticle interaction with the cancer cells are shown in Figure 8(d). The optical and mechanical effects of the bubble can be controlled through the laser parameters in order to tune the bubble to a diagnostic or therapeutic task (El-Sayed et al. 2005, 2006, Zhao et al. 2009).

Figure 8. Schematic of cancer cells disruption: (a): gold nanoparticles are injected to the target site; (b): gold nanoparticles interact with ultra-short laser pulse, where photothermal bubbles are generated around gold nanoparticles; (C): photothermal bubbles mechanically disrupt and remove the tissue, thus creating a channel.

Conclusion

We have proposed an interesting concept in which ultra-short temporal and spatial soliton pulses in the ranges of pico- and femtosecond can be generated using a MRR system. We have shown that a large bandwidth of the arbitrary soliton pulses can be compressed within a microwaveguide. The chaotic signal generation using a soliton pulse in the nonlinear microring resonators has been presented. A selected ultra-short light pulse can be localized and used to perform thermal-based killing of abnormal cells, tumors, and cancer. Laser pulses interact with a gold nanoparticle and generate optical and mechanical heating effects, which cause increasing temperature around the abnormal cell, leading to the cleaning and removal of the target.

Acknowledgement

We would like to thank the Institute of Advanced Photonics Science, Nanotechnology Research Alliance, Universiti Teknologi Malaysia (UTM), and King Mongkut's Institute of Technology (KMITL), Thailand, for providing research facilities. This research work has been supported by UTM's Tier 1/Flagship Research Grant, MyBrain15 Fellowship/MOHE SLAI Fellowship, and the Ministry of Higher Education (MOHE) research grant.

Declaration of interest

The authors report no conflicts of interest. The authors alone are responsible for the content and writing of the paper.