Finite element modeling for soft tissue surgery based on linear and nonlinear elasticity behavior

Abstract

New surgical techniques require fine control from the surgeon's point of view. Until recently, the necessary experience was only obtainable through traditional training protocols (using cadavers, animals, etc.). However, numerous training simulators have now been developed for use in this area. We present a new approach based on a three-dimensional finite element software and on different kinds of linear and nonlinear elastic constitutive equations that is able to predict realistic results. To classify these equations in terms of accuracy, we performed ex-vivo experimental measurements on lamb kidneys. The software has been applied to soft tissue deformation, namely lamb kidney and human uterus, and the numerical results have been compared to experimental ones.

• Surgical simulation
• 3D finite element modeling
• soft tissue elastic behavior

Introduction

New surgical procedures are increasingly complex and require specific training to guarantee surgeon qualification. Simulators have been developed to overcome the drawbacks of more traditional training systems, such as training on cadavers, live animals or real patients under the supervision of experts.

There are two main types of simulator. Those of the first type are based on a real-time approach, and are designed mainly for teaching or assessment purposes. They are often coupled to force-feedback systems, but frequently use simplifying assumptions [1], [2] (such as non-realistic constitutive equations) or simplified mechanical models (such as mass-spring systems) that lead to approximate results and provide a numerical response that can be quite different from real-life surgery.

Simulators of the second type are devoted to very accurate modeling of a given surgical procedure in order to optimize it (i.e., by determining the best operation sequence, etc.). In this case, the primary concern is the quality of the result rather than the response time [3].

This paper describes our approach, which clearly belongs to the second of the above categories by virtue of using a fine mechanical model in conjunction with a complete finite-element approximation and a precise identification procedure for soft tissue constitutive mechanical parameters. An application to modeling some classical surgical gestures in non-invasive gynaecological surgery is also presented.

An additional aim of this paper is to investigate the potential of different constitutive equations in predicting the mechanical response of soft tissues within a range of prescribed deformations. To determine which equation is best, we ran mechanical tests and compared the experimental measurements to numerical results.

Materials and methods

Numerical approach

Our computer code was developed on the basis of a 3D finite element numerical model which was itself developed in our laboratory, based on a step-by-step approach that is suitable for large plastic deformation and complex mechanical loads, and treating evolving contact conditions with tools [4].

Soft tissue mechanical behavior

(1) The linear approximation. As a first approach, the mechanical behavior of soft tissues can be considered as linear if the relative displacement with respect to the size of the organ is small, i.e., if local strains are smaller than 10% [5].

The classical linear elastic law of Hooke [equation (1)] is well suited for small strains and is easy to implement:where λ and μ are the Lamé coefficients, I the unit tensor, σ the Cauchy stress tensor, and ε the strain tensor defined from the displacement field u:Equation (1) can be rewritten aswhere s is the deviatoric stress tensor and κ is the compressibility coefficient.

Note that linear elastic incompressibility is expressed by:

When gravity forces are included and the inertia forces are neglected as a first approximation, the equilibrium equation is written asand the problem must be solved in terms of the unknown fields u and p.

There are three main kinds of boundary conditions for this problem:

• a kinematics boundary condition, due to the prescribed displacement, or velocity, of the surgeon's tools;

• a free-stress boundary condition on the free surface of the organs; and

• a non-penetration contact condition between the organs.

For any virtual velocity field v* and pressure field p*, the mixed integral formulation can be written as follows:

(2) Non-linear behavior. In surgery, local deformations often exceed the small strain assumption, and therefore the linear approach can no longer be used. According to references 2 and 5, a hyper-elastic model is preferable. The constitutive equation will be defined in terms of the following functions:

• i) the deformation gradient:where X is the coordinate of the material point in the non deformed configuration;

• ii) the Jacobian determinant: (For incompressible materials we impose J = 1.)

• iii) the Cauchy-Green stress tensor:

• iv) The first two invariants I₁ and I₂ of B.

The simplest non-linear, incompressible, elastic behavior is the Neo-Hookean model, in which the Cauchy stress tensor is written as follows:where p′ is a scalar field, homogeneous to a pressure field.

The Mooney-Rivlin constitutive equation is slightly more complicated:When the non-linearity is more severe, we can also use an exponential law of the form [2]For incompressible non-linear elastic material, the mixed formulation will be written as follows:Moreover, due to evolving contact with the surgical tools, the numerical model must use an incremental approach. The unknown is now the velocity field v^t at time t. The displacement vector will be updated according toand the incremental mixed formation becomesThe new deformation gradient at time t + Δt is evaluated according towhere the increment is computed byThe Jacobian determinant becomesIf J^t = 1 at the beginning of the increment, equation (19) can be approximated by linearization as

Finite element discretization

The tetrahedral element is probably the most convenient element for 3D meshing and remeshing of complex shapes. However, the classical linear interpolation is not compatible with incompressible or quasi-incompressible behavior [6]. For this reason, the space discretization is based on a tetrahedral mini-element, as illustrated in Figure 1.

Figure 1. Tetraheadral P1 + /P1 mini-element [4].

The velocity field v is interpolated in terms of the nodal values V_n of the velocity, and of the shape functionsN_n, defined in each sub-tetrahedron:The pressure field p is discretized using nodal values P_m, and the linear shape functions M_m in the tetrahedron:Using the finite element discretization equations (21) and (22) and the mixed integral formulations allows us to write a non-linear set of equations in terms of the V and P vectors of nodal unknowns, which is solved iteratively by using the Newton-Raphson method at each time step.

Remeshing and contact analysis

During the simulation of a surgical intervention, organs will often undergo large deformations, so that elements become highly distorted and consequently inappropriate for further finite element computation. An efficient remeshing procedure is used to regenerate locally those elements that are in contact with the tools and those that are too distorted [6]. Remeshing is also mandatory when dealing with surgical dissection, as this induces important topological modifications. Several tests are carried out after each time increment to evaluate the quality of elements, by comparison to a reference standard, and contact adaptation. The total number of nodes is, of course, kept as low as possible to avoid long computation times.

When non-linear behavior is used, the F matrices are updated using equation (17), stored for the next time increment, and interpolated when remeshing occurs.

Experimental and numerical setups

To classify the constitutive equations (1), (11), (12) and (13) in terms of accuracy, we carried out ex-vivo experimental measurements on lamb kidneys. In parallel, the different constitutive equations were introduced into the computer code. We then identified the best fit parameters for the different models by selecting the ones that led to computed measurable quantities (such as force versus displacement) that were close to the experimental ones under the same conditions (Figure 2). To obtain the most accurate results, the associated mechanical test should be as close as possible to classical surgical solicitations [7], [8]. The one selected here is an indentation test. The shape of the indentor was chosen so as to be as close as possible to that of a surgical forceps (diameter 5 mm). The 3D kidney geometry used for the simulation must also be as close as possible to that of the real kidney on which the experiments are performed. The 3D model was designed using CAD software.

Figure 2. Experimental (a) and computed (b) results for a lamb kidney indentation.

Results

Comparison between experimental and computed results

The kidney identification results are shown in Figure 3 and summarized in Table I. Identified parameters for linear behavior (Young's modulus: 0.02 MPa) lead to a good agreement for small strains (indentor displacements < 3 mm), but the computed forces are underestimated for larger strains.

Figure 3. Comparison between experimental and computed results for different constitutive equations (lamb kidney).

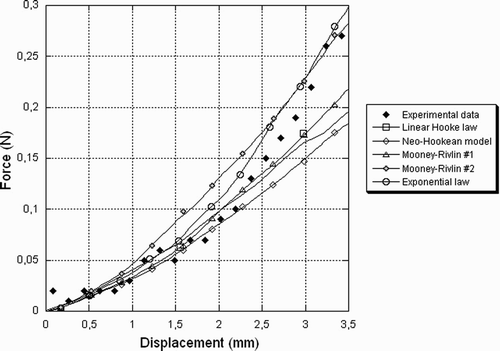
Table I.  Identification results for lamb kidney.

Law	Parameters		Least square estimation
Linear Hooke's law	Young's  Modulus = 0.02 MPa		14.18 %
Neo-Hookean law	c = 0.0034 MPa		8.12 %
Mooney-Rivlin 1	c1 = 0.00034	c2 = 0.00306	3.48 %
Mooney-Rivlin 2	c1 = 0.0004	c2 = 0.004	3.74 %
Fung-Demiray	μ = 0.0067	γ = 5.0	1.75 %

The best identified parameter for the neo-Hookean model does not fit well with the experimental data and thus does not provide improved results with respect to the linear elastic Hooke's Law. The Mooney-Rivlin constitutive equation (with two different parameters sets) gives better results, but computed forces are still underestimated for larger strains (Mooney-Rivlin #1) or always overestimated (Mooney-Rivlin #2). Finally, the exponential Fung-Demiray law, with an appropriate choice of parameters, gives a good match between numerical and experimental results.

Application to gynaecological surgery

Figure 4 shows the modeling of two different cases that can occur in gynaecological surgery. For a qualitative comparison, motion pictures were recorded during a surgical operation. As a first approximation, the computed results were obtained for a linear Hooke's Law initialized with the previously identified parameters of the kidney.

Figure 4. Qualitative comparison between a real surgical procedure (a, b) and computed results (c, d) for uterine palpation (a, c) and tubal mobility exploration (b, d).

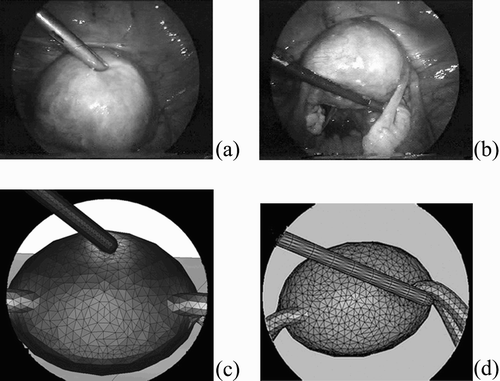
The first case deals with uterine palpation and the second with the exploration of tubal mobility in gynaecologic explorative surgery. The mechanical parameters used in these cases are derived from the soft tissue identification procedure introduced earlier. Deformation visualization was performed in these two cases and compared qualitatively with video recordings of a real surgical operation. This case shows that our model gives good quality results and that the three procedures of i) remeshing, ii) contact analysis, and iii) taking gravity into account have performed well and can deal with the various solicitations which can be observed during a surgical operation.

Discussion

Results obtained with a linear elastic law confirm that the small strain assumption is not accurate for these ranges – thus the need to use a hyper-elastic law.

The different results obtained with the various hyper-elastic constitutive equations can be of prime importance when dealing with coupled multi-organ systems. In such cases, a small difference in geometrical deformation when a force is prescribed can induce large differences in the displacements of other organs that are in contact. For future coupling with a haptic device, the force feedbacks will be higher when using a non-linear law, and thus the simulation should be more realistic than with a linear one.

The data gathered through this study will enable us to obtain a more accurate prediction of organ deformations when using virtual surgery modeling. We have shown that a combination of experimental measurements and numerical modeling can provide useful information for virtual reality simulations. The good quantitative fit of our numerical results with the experimental data is encouraging. In the case of the kidney, an exponential stress-strain law (with two parameters) seems to model accurately its mechanical behavior. The finite element model must now be extended to deal with more complex and realistic solicitations by modeling multi-organs interactions. For even more realistic simulation of the material behavior, a viscosity component will be added to the hyperelastic one in the near future. Indeed, the characteristic time for the exponential creep/recovery curve of soft tissues ranges from seconds and minutes, so viscoelasticity should be taken into account for better predictive results when deformation duration is of the same order of magnitude. For longer time scales, however, this can be assumed to be negligible.