Real-time tracking of vertebral body movement with implantable reference microsensors

Abstract

Objective: In the spine, navigation techniques serve mainly to control and accurately target insertion of implants. The main source of error is that the spine is not a rigid organ, but rather a chain of semiflexible movement segments. Any intraoperative manipulation of the patient alters the geometry and volumetry as compared to the 3D volume model created from the image data. Thus, the objective of the study was to implement the theoretical principle of microsensor referencing in a model experiment and to clarify which anatomical structures are suitable for intermittent implantation of positional sensors, as illustrated with cervical vertebral bodies.

Materials and Methods: Laboratory tests were conducted using 70 models of human cervical vertebral bodies. The first experiment investigated whether arbitrary movements of vertebral bodies can be tracked with the positional information from the implanted microsensors. The accuracy of this movement monitoring was determined quantitatively on the basis of positional error measurement. In the second experiment, different ventral and dorsal surgical operations were simulated on five models of the cervical spine. Quantifiable measurement values such as the spatial extension of the intervertebral space and the relative positions of the planes of the upper plates were determined.

Results: With respect to the differing anatomy of the individual vertebral bodies of the cervical spine, the sensors could be placed securely with a 5 × 2 mm drill. The registration error (RE) was determined as a root mean square error. The mean value was 0.9425 mm (range: 0.57–1.2 mm; median: 0.9400 mm; SD: 0.1903 mm). The precision of the movement monitoring of the vertebral body was investigated along its three main axes. The error tolerance between post-interventional 3D reconstruction and direct measurement on the model did not exceed 1.3 mm in the distance measurements or 2.5° in the angular measurements. The tomograms on the system monitor could be updated in close to real time on the basis of the positional information from the reference sensor.

Conclusions: Motion sensors implanted into the vertebral bodies communicated any change in position to the navigation system in close to real time, thus enabling the preoperative image data set to be updated. The experiments described could ultimately show that continuous real-time visualization of individual vertebral body movements along the movement axes (flexion-extension, tilting and rotation) is possible with high accuracy using implantable microsensors. A future application of such microsensors might be the integration of robot systems into spinal microsurgery.

• Image-guided surgery
• spinal navigation
• microsensors
• vertebral body movement
• real-time tracking

Introduction

Neuronavigation systems have been used in cranial neurosurgery since the mid 1980s [1–3]. Owing to the rapid technological development in the field of image processing and in computer technology, such navigation systems are now used routinely. They are helpful not only in intraoperative anatomical orientation, but also in delimitation of healthy from pathological processes and in achieving accurate alignment of instruments at the operation site. However, navigation techniques used in the spine serve mainly to control and accurately target insertion of implants [4–9].

The placement of pedicle screws is of particular importance. The screw's point of entry and its course through the pedicle into the vertebral body is planned using tomographic data that is mostly obtained preoperatively. Intraoperative placement of an implant can be optimized by comparing the image and planning data with the operation site. Besides the known technical imprecisions of the various navigation techniques [10], [11], the main source of error is that the spine is not a rigid organ, but rather a chain of semiflexible movement segments. Segments including more than one vertebral body are regarded as rigid structures, although it is precisely the relative position of the affected vertebral bodies and articular surfaces that plays a crucial role in determining the extent of later function and freedom from symptoms experienced by the patient. Consequently, each scan image only represents a snapshot of the spine, and any intraoperative manipulation of the patient leads to altered geometry and volumetry as compared to the 3D volume model created from the image data. Particularly in diseases of the cervical spine due to arthrosis, there are both osseous and discoligamental structural changes which can substantially alter the biomechanical function and statics of the cervical spine. This results in painful instabilities of one or more segments and compression syndromes due to stenosis of the spinal canal and neuroforamina. Continuous intraoperative 3D imaging of the joint and vertebral body positions would provide important information for predicting the postoperative biomechanical result in patients with such spondylarthritic changes, and also in fracture cases.

One approach to solving the problem consists of refreshing the image information by intraoperative imaging (intraoperative CT and/or fluoroscopy) [5], [12–13]. In this way, the respective positions of the osseous structures can be recorded at any time during the procedure, which is a prerequisite for precise surgery. Reference points firmly attached to the vertebral body that are independent of the physical principle of the navigation technique (optical, sonographic or electromagnetic) are used to register mechanically induced structural shifts in the operation site [14]. It is wrongly assumed that a force acting locally spreads evenly over several segments of the spine and that structural changes corresponding to a rigid model can be postulated (Figure 1). This is shown not only by biomechanical investigations [15], [16]: The inhomogeneity of the movements within the individual movement segments can be demonstrated most graphically by means of intraoperative transillumination. Various mathematical models have been developed to calculate such intersegmental movement transmissions provoked by the surgical intervention and to use them for updating the image data [16–20]. However, most of these mathematical approaches fail due to the complexity of the factors affecting a movement transmission via a discoligamentous intervertebral space or the complexity and duration of the calculation process, which make it impossible to use this information within the normal course of an operation.

Figure 1. It is wrongly assumed that a force acting locally spreads evenly over several segments of the spine.

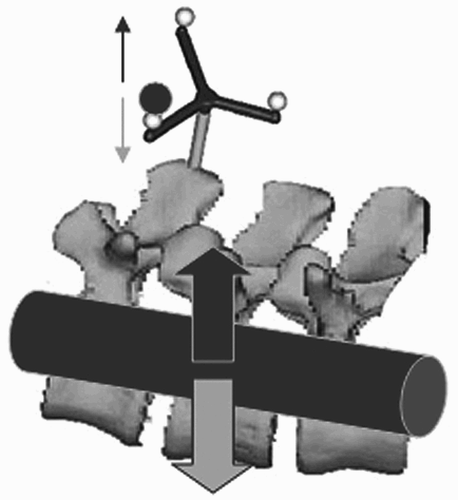
In the authors' opinion, an alternative would be to track each individual segment that is a rigid entity independently within the multisegmentally mobile spinal chain via an individual reference. It is assumed that structural deformations ultimately occur only in the soft-tissue compartments, i.e., in the region of the intervertebral discs, the articular capsules and the ligamental apparatus. The bony structures of each individual vertebral body are not deformable, so that after successful completion of the calibration process the movement of a vertebral body can be tracked with a firmly fixed reference point. If every individual vertebral body within a surgical site were to have its own reference point, each could be localized with appropriate computation and its spatial movement followed independently, along with its spatial relationship to the adjacent vertebral bodies. However, the reference systems available to date take up so much space that it is impossible to apply several of these simultaneously at one surgical site. With increasing miniaturization, however, positional sensors that can be used to determine the position and movement in six degrees of freedom (DOF) using an electromagnetic navigation technique have become available for the first time. The dimensions of these sterile encapsulated sensors theoretically allow them to be implanted directly into the relevant vertebral bodies for the duration of the operation then removed at the end of the navigation. In this way, the intraoperative movements of each vertebral body can be followed independently and in relation to adjacent segments without the reference system obstructing the operation.

An objective of the present study was therefore to implement the theoretical principle of microsensor referencing in a model experiment and to clarify which anatomical structures are suitable for intermittent implantation of positional sensors, as illustrated with cervical vertebral bodies. A further objective was to investigate to what extent and with what degree of precision individual vertebral body movements can be identified using implanted reference microsensors, and whether their relative positions can be defined computationally and by imaging with the help of simultaneous data recording and processing from several microsensors working in parallel in adjacent vertebral bodies.

Materials and methods

Vertebral body models

The laboratory tests were conducted using ten anatomical plastic models of the cervical spine (70 vertebral body models) from different production series of various manufacturers (including 3B-Scientific models A72, A21 and A58/1, Stockburger model ERL 4073/1, and Rüdiger model A213). In five of these models, the vertebral bodies C1 to C7 were isolated to register image data for later investigations of isolated vertebral body motion. The other five models were used to simulate operations on a movement segment consisting of two vertebral bodies and one intervertebral space.

Scan protocol

Five series consisting of isolated cervical vertebral body models (C1 to C7) and five connected cervical spine models (occiput-C0/C1 to C 7) were scanned to create a 3D image data set in a high-resolution spiral CT (Siemens Somatom Volume Zoom™). The layer thickness was 1 mm, and the other scan parameters were as follows: gantry tilt 0°, kernel H70, layer collimation 1 mm, table advancement/rotation 2.6 mm, matrix 512 × 512, 120 kV, eff. 200 mAs. The image data obtained were transferred via CD to the navigation system in DICOM format.

Navigation system

The electromagnetic navigation system ACCISS II™ (Schaerer Mayfield Technologies, Berlin, Germany) was used to carry out sensor-based navigation. This DC electromagnetic navigation technique works by detection of (macro-) sensors within a pulsed, homogeneous electromagnetic field. The commercially available sensors employed for this purpose are 8 mm × 8 mm × 18 mm in size with a weight of 1.2 g. They have 6 DOF (position and orientation) with an angular range of ± 180° azimuth and roll and ± 90° elevation. The static accuracy is specified by the manufacturer as 1.8 mm RMS (position) and 0.5° RMS (orientation). The static resolution is 0.5 mm (position) and 0.1° (orientation) at a distance of 30.5 cm from the transmitter. The rate of measurement is approximately 120 measurements/second. If required, the sensor can be accommodated in a watertight capsule and is connected to the navigation system with a 3-meter cable. These sensors are integrated into various pointers and surgical instruments in the version offered by the manufacturer, or serve as an additional point of reference in cranial navigation, e.g., to monitor intraoperative head movement. The intraoperative precision of the system and its substantially reduced susceptibility to interference from external metallic influences owing to the DC technique employed (as compared to conventional AC electromagnetic navigation techniques) has already been reported [21], [22]. Altogether, with a prototype module and the software version 1.9 of the ACCISS II™ platform, the system can operate up to four different sensors at once.

The microsensors used are a miniaturization of the macrosensors previously described. They have a diameter of approximately 1.8 mm, and a length of approximately 8.4 mm including the sterilizable capsule (Figure 2). The sterile sheath encloses the cable emerging from the sensor up to the connector as a continuous catheter in which the sensor is the tip of the catheter. The rigid part of the tip is approximately 10 mm long, so at least half this length (i.e., approximately 5 mm) should rest in the bone for a secure hold. The measurement of position of the microsensors is performed with a frequency of 90/s; positional data can be registered in 6 DOF, including the Cartesian coordinates for the X, Y and Z orientations. Further specifications from the manufacturer (Ascension Technologies Corporation, Burlington, VT, USA) are as follows: Translation range is from 20 cm to 71 cm in X, ± 30 cm in Y and Z. In the forward hemisphere, angular range is ± 180° for azimuth and roll; ± 90° for elevation. Static accuracy is 1.4 mm root mean square (rms) position, 0.5° rms angular. Static resolution is 0.05 mm (position) and 0.1° (orientation) at 30.5 cm from the transmitter.

Figure 2. The microsensors have a diameter of approximately 1.8 mm and a length of approximately 8.4 mm including the sterilizable capsule.

Measurement procedure and its accuracy

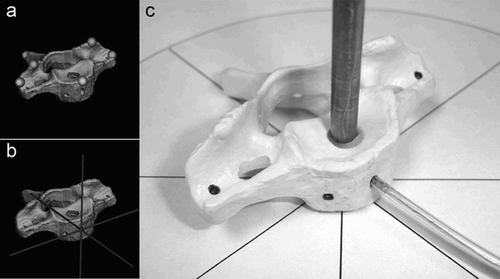
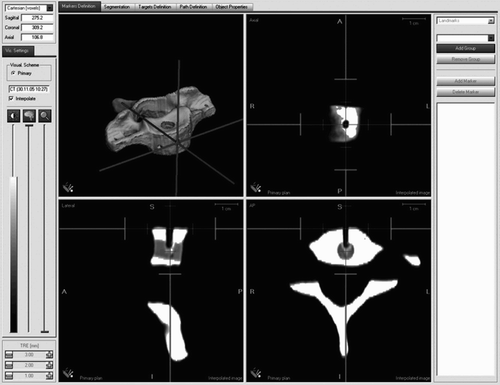
The image data information was processed in the navigation system using an auto-segmentation algorithm of the ACCISS II™ system software version 1.9. The image data was registered by point-to-point matching. For this purpose, eight prominent landmarks in the vertebral body - the transverse processes, the joint facets and the spinous process - were predefined (Figure 3a). Data acquisition entailed sequential scanning of the landmarks with the pointer of the navigation system. The positional data was recorded manually by pressing a button on the pointer. The respective vertebral body model was not fixed for the measurement process, since the implanted and firmly anchored microsensor was used as a point of reference. The method and location of microsensor fixation is described in more detail in the Results section.

The registration error (RE) as root mean square (rms) was calculated as a criterion for the quality of the calibration accuracy of the image data registration and shown on the system monitor. The RE is a qualitative value for the distance between the positions of the predefined measurement points in the image data and the actual positions of the landmarks in the model.

The RE (rms) values specified below are calculated as follows:Formula A: Registration error, RE (R = registration matrix; N = number of points; y_i and x_i = main coordinates in the corresponding coordinate system; t = translation part)

Experimental design and determination of working accuracy

The first experiment was designed to investigate whether arbitrary movements of the vertebral bodies can be tracked with the positional information from the implanted microsensor after completion of image data registration. The accuracy of this movement monitoring was determined quantitatively on the basis of the positional error (PE) measurement. For this purpose, the Cartesian data from five target points (T1–T5) were determined with the pointer-based manual data acquisition in a 0° initial position. After any given change of position, the same target points were measured once more. The spatial deviation of the coordinates was calculated as PE using the following formula:Formula B: Positional error, PE (x, y, z = Cartesian spatial coordinates; n = target 1–5)

The vertebral body was rotated in 45° increments (Figure 3b–c) around the longitudinal, sagittal and transverse axes through the respective vertebral bodies and displaced linearly in 10-mm increments along the same axes. The PEs calculated were intended to provide information as to the precision with which target points can be found again after arbitrary movement of the vertebral body, and whether the extent and direction of the vertebral body movement can affect the accuracy of the movement monitoring. PE values were determined for the vertebral bodies C1 to C7 from five models of the cervical spine, i.e., a total of 35 vertebral bodies. To reduce system-specific errors, all PE calculations were repeated five times for each axis in every angular position and direction of displacement.

Figure 3. (a) 3D segmented vertebral body with landmarks for point-to-point registration. (b and c) Vertebral body model (c) and 3D segmented model (b) during position error (PE) measurements along the sagittal axis.

Simulated surgical operations on movement segments

Three ventral and two dorsal surgical operations were simulated on five complete models of the cervical spine. A bone cement (Palacos™) implant was used for ventral fusion in segment C2/3. A ventral plate osteosynthesis was performed in segment C5/6, and a ventral fusion with cage implantation in segment C6/7. A foraminotomy was carried out on the left side from dorsal in segment C3/4, and a dorsal screw/bar osteosynthesis in segment C5/6. In all five operations, a 3D image data set was first obtained and the corresponding segment consisting of two vertebral bodies and the intervertebral space was represented as a 3D model. Both vertebral bodies were fitted with a microsensor, and the image data was registered separately for each body. The two sensors were assigned to their respective 3D vertebral body models within the system, and the spatial orientation of the two vertebral bodies relative to one another was imaged. Quantifiable measurement values such as the spatial extension of the intervertebral space and the relative positions of the planes of the upper plates were determined. The operations were then carried out with the microsensors in place. At the end of each intervention, the 3D image of the corresponding movement segment that had been updated using the positional data of the microsensors was calculated in the same way. The values for the relative positions of the upper plates and the dimensions of the intervertebral space were determined once more. These were compared with the initial values to check whether changes in the relative positions of the vertebral bodies could be registered. Finally, the computed 3D postoperative reconstruction was compared with a digital photograph of the cervical spine model after the intervention with regard to outward appearance and relative angular dimensions of the vertebral bodies (Figure 4).

Figure 4. Computed 3D reconstruction before (c) and after (d) simulated cage-fusion C6/7 compared with a digital photograph of the pre- and post-interventional spine model (a and b).

Results

Fixing of microsensors in the vertebral body

Due to the differing anatomy of the individual vertebral bodies of the cervical spine, different locations were sought for intermittent implantation of microsensors. In each case, the drill hole had to be at least 5 mm deep and 2 mm in diameter to assure a firm and non-displaceable anchorage of the sensor. In addition, the different options for attachment in ventral and dorsal access to the cervical spine were to be investigated for later clinical implementation (Table I). The local fixation in the drill channel was ensured by use of bone wax to fill the hollow spaces between the sensor and the drill hole wall and by the anchorage of the sterile sensor capsule fitted with anchoring vanes.

Table I.  Sites of microsensor implantation

	Ventral approach	Dorsal approach
	Corpus vertebrae	Processus spinosus	Massa lateralis
C1	−	−	+
C2	+	(+)	−
C3	+	+	+
C4	+	+	+
C5	+	+	+
C6	+	+	+
C7	+	+	+

+=adequate fixing possible with a 5 × 2 mm drill hole;−=adequate fixing not possible.

Preferentially, the corpus of the vertebral body was chosen for attachments to the ventral side of the cervical spine (Figure 5). Since a central screw for the locking systems must be set in most ventral instrumentations and the access route through the soft tissue of the neck is mostly from the right, the optimal placement site appears to be the left lower quadrant of the vertebral body. It was not problematic to fix the sensors there because the corpus diameter from C2 to C7 averaged 12–17 mm in all cases. An adequate fixation to the ventral side of C1 was not possible.

Figure 5. Due to the differing anatomy of the individual vertebral bodies of the cervical spine, different locations were sought for the intermittent implantation of microsensors.

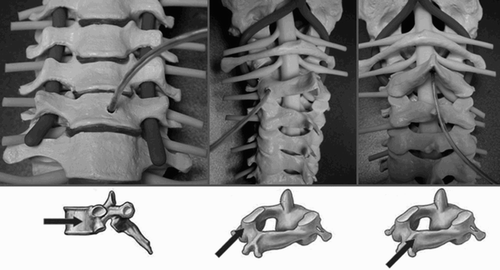
Both the spinous process and the lateral mass are suitable for attachments to the dorsal side of the vertebral bodies (Figure 5). In all models, a mono- or bicortical drill channel at least 5 mm long and 2 mm in diameter could be made in the spinous process at the level of C3 to C7 without breaking into the spinal canal. However, owing to anatomical variants of C2 (in some cases, an extremely short spinous process or duplication thereof), a firm hold for the sensor may not be attained in a third of cases. This is also reflected in the anatomical models used, although these do not, of course, take into consideration the putative norm variants in the population. In drilling the 5-mm channel in the lateral mass, a procedure was applied comparable to that used in inserting lateral mass screws for cervical instrumentation. At the level of C1, this means that the drill channel passes in the sagittal plane, rising slightly in relation to the interarticular space C1/2 and perpendicular to the frontal plane. The drill hole enters below the dorsal arch of the atlas at its transition to the lateral mass C1. At the level of C3 to C7, the drill hole enters 1–2 mm to medial and cranial from the center of the lateral mass. The channel should diverge 20–30° to lateral and parallel to the superior articular facet in the direction of the anterolateral boundary of the superior articular process. However, drilling in the region of the isthmus of C2 appears to be difficult and impractical owing to the confined anatomical situation of the nerve structures and the closeness to the vertebral canal.

Measurement accuracy

The registration error (RE, formula A) was determined as an rms error for the measurement accuracy. The vertebral bodies C1 to C7 were measured in five different models of the cervical spine. The mean value of 35 RE measurements was 0.9425 mm (range: 0.57 to 1.2 mm; median: 0.9400 mm; SD: 0.1903 mm). The anatomical form (e.g., C1 as compared to C7) had no statistically significant effect on R.E.

After successful registration of the image data, the 3D reconstruction model of the respective vertebral body could be imaged together with the axial, transverse and sagittal tomographic planes on the system monitor (Figure 6). The Cartesian coordinates of the five predefined targets (T1–T5) could be determined using a manual pointer and stored for calculation of the P.E.

Figure 6. System monitor screenshot showing the 3D reconstruction model and axial, transverse and sagittal tomographic planes.

Tracking of a vertebral body

The precision of the movement monitoring of the vertebral body was investigated with respect to the three main axes: sagittal (S), transverse (T) and longitudinal (L). For this purpose, the mean positional error (PE_r, formula B) calculated per vertebral body from five targets (T1–T5) was measured around the respective axis after rotation in 45° increments (Figure 3c). In addition, the mean positional error (PE_s, formula B) was determined in 10-mm increments in linear displacement along the axes (+30 mm to−30 mm).

The PE_r and PE_s values shown in Figures 7 and 8 in turn reflect the mean value for the measurements for all 35 vertebral bodies for the corresponding movement relative to the axes S, L and T. There were positional imprecisions of between 0.60 and 1.63 mm for the rotation around the sagittal axis, PE_r-S; between 0.75 and 1.61 mm for the transverse axis, PE_r-T; and between 0.73 and 1.46 mm for the longitudinal axis, PE_r-L. For displacment, positional imprecisions were between 0.68 and 1.52 mm for the sagittal axis, PE_s-S; between 0.76 and 1.53 mm for the transverse axis, PE_s-T; and between 0.59 and 1.61 mm for the longitudinal axis, PE_s-L.

Figure 7. Mean position errors (PE_r) for rotation around the longitudinal (a), sagittal (b) and transversal (c) axes.

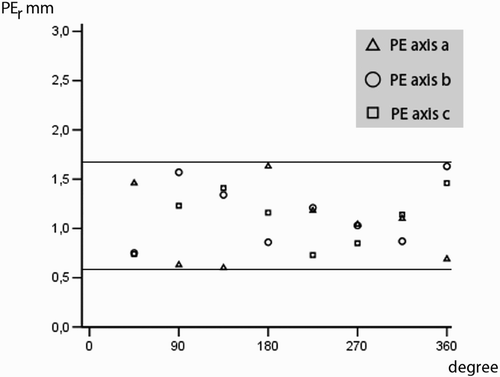
Figure 8. Mean position errors (PE_s) for displacement/shift along the longitudinal (L), sagittal (S) and transversal (T) axes.

The tomograms on the system monitor could be updated on the basis of the positional information of the reference sensor. The images were close to real time, with a computational delay averaging less than 0.5 s. The 3D reconstruction model could be aligned semi-automatically by viewing individual images in the site view mode. The computation time required to process and to create the adjusted 3D image averaged 3.4 s (±0.9 s).

Tracking of several vertebral bodies at once

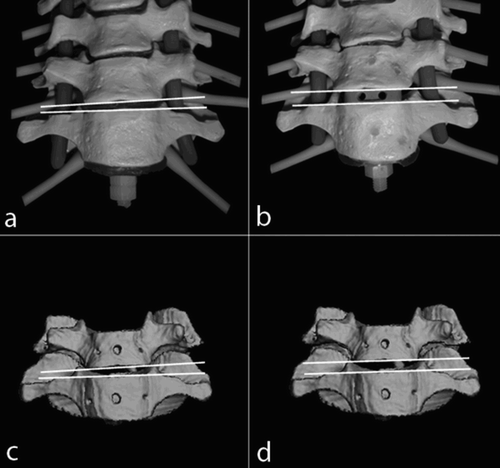
During the simulated surgical operations on movement segments with two vertebral bodies, the pre-interventionally calculated 3D reconstruction models were compared with the postoperative volume models with corrected alignment based on positional information from the microsensors. The following parameters were determined: (1) position of the vertebral body upper plates relative to one another (λ = 0° indicated they were exactly parallel); (2) height of the individual space in the a.p. projection (a in mm); (3) distance of the anterior edges of the body in the lateral projection (b in mm); (4) distance of the spinous processes from each other in the lateral projection (c in mm); and (5) angular relationship of the spinous processes in the craniocaudal projection (δ = 0° entails an exact superimposition of the spinous processes) (Figure 9).

Figure 9. During the simulated surgical operations, the relative positions of the vertebral body upper plates (λ), the height of the individual space in the a.p. projection (a), the distance of the anterior edges of the body in the lateral projection (b), the distance of the spinous processes from each other in the lateral projection (c), and the angular relationship of the spinous processes in the craniocaudal projection (δ) are determined.

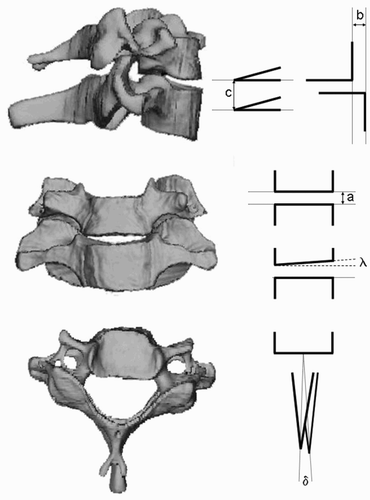
Alterations in the measurement values document the movements of vertebral bodies relative to one another, as recorded by the microsensors. These were induced iatrogenically by the forces applied in the operation. An example of this can be seen in Figure 4, which shows a ventral fusion C6/7 with implantation of a 4 × 18 mm cervical SHELL cage (Advanced Medical Technologies (AMT), Germany). After milling out the intervertebral space of approximately 2.5 mm and implanting the cage, the space is opened to 4 mm. After the intervention, the slight inclination of the upper plate to the right (λ = 6°) has almost been eliminated by introduction of the plane-parallel cage (λ = 5°). The operation was carried out with stable rotation (δ = 0° pre- and postoperatively). The distance between the spinous processes was reduced by 1.3 mm as a result of the ventral opening.

The smallest biomechanical changes were in foraminotomy, and the most pronounced in the ventral fusion with Palacos interponate. The detailed measurement values are presented in Table II. To enable comparison of the recorded positional changes with the actual results, measurements calculated on the 3D reconstruction model were also measured directly in the post-interventional model and documented by digital photographs. These measurement values are also shown in Table II. The error tolerance between post-interventional 3D reconstruction and direct measurement on the model did not exceed 1.3 mm for the distance measurements or 2.5° for the angular measurements in any of the five cases.

Table II.  Biomechanical changes after different surgical procedures.

	1		2		3		4		5
	degree		mm		mm		mm		degree
	λ pre	λ post	a pre	a post	b pre	b post	c pre	c post	δ pre	δ post
Ventral fusion with bone cement C2/3	4.0	1.0	2.6	5.0	1.0	0.4	2.5	0.4	0	1.5
Ventral plate osteosynthesis C5/6	3.0	2.0	2.8	2.9	0	0.2	2.2	2.3	0	1.0
Ventral fusion with cage C6/7	4.0	0.5	2.5	4.0	1.0	1.0	3	1.7	0	0
Foraminotomy C3/4	2.5	2.5	2.5	2.5	0.8	0.7	2.6	2.5	0	0
Dorsal screw/bar osteosynthesis C5/6	3.0	2.0	2.6	2.5	0.8	0.2	2.2	2.4	1.0	3.0

λ = relative positions of vertebral body upper plates; a = height of individual space in a.p. projection; b = distance of anterior edges of body in lateral projection; c = distance of spinous processes from each other in lateral projection; δ = angular relationship of spinous processes in craniocaudal projection; pre = pre-interventional; post = post-interventional.

Discussion

The importance of spinal navigation has increased in recent years. Various study groups have reported that spinal navigation ensures better anatomical orientation, thereby increasing the safety of the operation [6], [13], [23], [24]. However, most clinical use of spinal navigation is confined to navigated placement of pedicle screws. A large number of studies have documented that the rate of incorrect placement of pedicle screws can be significantly reduced using spinal navigation techniques [4], [5],[7–9],[12], [25], [26]. However, a disadvantage of spinal navigation is that preoperative image data sets are used to visualize intraoperative processes. Since conventional spinal navigation systems regard the segment to be operated on as a rigid system, the intraoperative positions of the individual vertebral bodies relative to one another do not necessarily reflect those in the pre-interventional images. Until now, it has only been possible to reduce this risk of possible intraoperative inaccuracy by updating the image data set with intraoperative CT or 3D fluoroscopy. However, this leads to a prolonged operation with much greater use of apparatus, as well as additional radiation exposure for the patient and surgical team in the case of intraoperative fluoroscopy.

A mathematical approach to tracking the continuous movement of individual vertebral bodies is the finite element model, in which an attempt is made by means of mathematical models to simulate the movements of ligaments, musculature and bony structures in response to forces acting on them [16-20]. This model can be used to calculate the action of various vector forces on the spine and to predict their effect on the musculoligamentous and osseous system of the spine [16]. However, until now, the intraoperative movements of the individual vertebral bodies could not be calculated using this approach owing to the limitations of computation capacity and the large number of vectors acting on the spine.

In this study, the individual vertebral bodies are segmented as single movement segments. Motion sensors are implanted into the vertebral bodies that communicate any change of position to the navigation system in close to real time and thus enable the preoperative image data set to be updated. The technical prerequisite for this was a distinct miniaturization of the macrosensors already used routinely in DC electromagnetic navigation [21], [22]. The microsensors used in this study have a diameter of less than 2 mm including the sterile capsule and can be placed directly into the vertebral bodies. The model investigations have shown that the sensors can be placed securely with a 5 × 2 mm drill. The risks of injuring the nervous structures surrounding the bone and the vertebral canal are probably equivalent to those known for spinal instrumentation with ventral screw plate systems [27] or dorsal lateral mass instrumentations [28]. However, evaluations of the first clinical applications are required for a precise appraisal. The invasive fixation technique would be risky, especially in traumatic etiologies or in osteoporotic patients. Further destabilization of the osseous structures by the iatrogenic manipulation cannot then be ruled out, so the first clinical test phase is confined to degenerative diseases.

The laboratory experiments described in this paper could ultimately show that continuous real-time visualization of the individual vertebral body movements along the movement axes (flexion-extension, tilting and rotation) is possible with high accuracy using implanted microsensors. The application precision is crucial for the clinical use of any navigation technique. It essentially describes the overall quality of the relative congruence between the “real world” of the operation site and the “virtual world” of the clinical image data. The application precision is affected by various factors. These include the accuracy of the image data set employed, the accuracy of the measurement technique used, various possibilities for error in the registration of image data, and external effects on the positional accuracy. Both the voxel size and geometrical distortions in imaging have a direct effect on the accuracy of the 3D image data set. The maximum possible deviation corresponds to the extent of one voxel and thus crucially depends on the layer thickness of the tomographic technique used. For CT with a 512 × 512 matrix, the voxel size is 0.65 mm × 0.65 mm × layer thickness (in mm). The mean error to be expected is calculated as voxel vector and amounts to 0.7 mm with the layer thickness of 1 mm laid down in the CT protocol used in this study.

The system accuracy of the electromagnetic navigation technique is essentially determined by the physical function principle, as well as by the hardware and software components implementing this principle. It is expressed technically by the positional precision and angular precision, i.e., by how accurately the position and the orientation of a sensor in space can be determined. For the electromagnetic microsensor employed in this study, the positional precision specified by the manufacturer is 1.0 mm (rms) and the angular precision is 0.5° (rms) over the entire measurement range.

The pivotal precision must also be considered when using a pointer instrument. This indicates the precision with which a moving instrument with a fixed tip can determine a fixed position in space. This value substantially depends on the length and diameter of the tip, as well as the care with which the calibration of the instrument had been carried out. For the standard stylus of the navigation system used in this study, the manufacturer specifies the pivotal precision as 1.2 mm.

Various measurement errors can be calculated as a measure for the quality of the image data registration. Inter alia, this is intended to enable comparisons between different navigation systems. In recent years, the nomenclature for analysis of measurement errors suggested by Maurer et al. [11, 29-31] has become accepted. Usually, the registration error (RE) is defined as a value for the measurement accuracy of the image data registration. The RE describes the distance between the position localized in the image data and the position measured in the operation site and transformed into the image coordinate system by means of the registration image. Important factors are the error in the positional measurement system used in determining the position in the operation site and the accuracy of the localization of the landmark positions in the image data set [11], [22], [31].

In the most unfavorable case, there may be an addition of all potential sources of error described previously, resulting in a positional inaccuracy. This is purely due to measurement error and may be potentiated by a factor of 4 to 5. In order to detect such a phenomenon at an early stage and be able to act on it, a fixed reference point should be checked at defined times over the entire period, thus checking the system for a fall in accuracy or the effect of external factors. In the ideal case, this could be a landmark that is virtually impossible to displace, such as the head of a small reference screw. However, there is controversy as to whether the introduction of a further invasive reference into the vertebral body is ethically justifiable.

Despite the substantial iatrogenic invasivity of the described technique, the authors consider it to have great clinical potential with a justifiable cost-benefit ratio. If laboratory results are successfully repeated in clinical applications in the operating theater, continuous monitoring of the biomechanical situation of the operated vertebral segment would be possible for the first time by means of the implantable microsensors. In particular, the optimal biomechanical alignment of the individual vertebral body segments, i.e., an alignment of the spine that is as physiological as possible, can be imaged in real time. This may be helpful in achieving a fusion of the spinal segments that is most physiologically favorable, especially in cases of spondylodesis of the spine, thereby improving the long-term outcome. For clinical use, the computation necessary for the real-time imaging must be minimized in order to be able to track more than two vertebral bodies simultaneously. The switch from on-demand to online imaging of the 3D reconstruction model must also be solved at the level of the system software. However, the problem of autosegmentation and isolated volume model calculation, as well as isolated representation of the position of several vertebral bodies, appears to have been solved with the prototype software version 1.9. Further studies with image data of pronounced spinal degenerations are required to show whether the segmentation algorithm chosen works adequately in the model, and also in clinical use.

A future application of implantable microsensors might be the integration of robot systems into spinal microsurgery [32], [33], for which continuous intraoperative imaging of the movement segment is also necessary. So far, this has only been possible by means of recalibration on the basis of intraoperative imaging. Implantable movement sensors could optimize the surgical precision of these systems by representing movement in real time and enable their clinical application.

The results reported above have encouraged the authors to commence a clinical testing phase.

Acknowledgements

This study was financed inter alia by funds from the Deutsche Arthroshilfe e.V and the Forschungsförderung der Charité-Universitätsmedizin Berlin (Research Fund of Charité University Hospital in Berlin). The authors also thank Dr. S. Schönherr and Mr. U. Warschewske (Schaerer Mayfield Technologies GmbH, Germany) for their technical assistance in the implementation of this project.