A topologically faithful, tissue-guided, spatially varying meshing strategy for computing patient-specific head models for endoscopic pituitary surgery simulation

Abstract

This paper presents a method for tessellating tissue boundaries and their interiors, given as input a map consisting of relevant tissue classes of the head, in order to produce anatomical models for finite-element-based simulation of endoscopic pituitary surgery. Our surface meshing method is based on the simplex model, which is initialized by duality from the topologically accurate results of the Marching Cubes algorithm, and which affords explicit control over mesh scale, while using tissue information to adhere to relevant boundaries. Our mesh scale strategy is spatially varying, based on the distance to a central point or linearized surgical path. The tetrahedralization stage also features a spatially varying mesh scale, consistent with that of the surface mesh.

Introduction

Virtual reality (VR)-based surgical simulation involves the interaction of a user with an anatomical model that is representative of clinically relevant tissues and endowed with realistic constitutive properties, by means of virtual surgical tools. This model must be sufficiently descriptive for the interaction to be clinically meaningful: it must also afford advantages over traditional surgical training in terms of improving surgical skill and patient outcome [1]. Our simulation application, endoscopic transnasal pituitary surgery, is a procedure that typically involves removing mucosa, enlarging an opening in the sphenoid sinus bone with a rongeur, making an incision in the dura mater, and scooping out the pathology with a curette, while avoiding surrounding critical tissues [2]. This entails anatomical meshing capable of accurately depicting the pituitary gland and the arteries and cranial nerves surrounding it, as well as the brain, relevant sinus bones, dura mater, and any imbedded pathology, as shown in Figure 1. This paper presents a method for tessellating tissue boundaries and their interiors, featuring surface and volume meshing stages, as part of a minimally supervised procedure for computing patient-specific models for neurosurgery simulation.

Figure 1. Endoscopic trans-nasal pituitary surgery: (a) OR set-up; (b) sagittal image of the head featuring the pituitary gland, parasellar bones, brain and cranium; (c) oblique image featuring the pituitary gland and surrounding critical tissues (reproduced with permission from reference [2]). [Color version available online.]

Our clinical application, in light of the presence of surrounding critical tissues and the correlation between lack of experience and surgical complications [3], is a good candidate for simulation. Furthermore, this application requires dense shapes in the field of view of the endoscope, while limiting the number of elements overall and still maintaining the conformality of the mesh. This argument justifies the application of a spatially varying mesh strategy. Furthermore, an important objective is the recruitment of finite element (FE) modeling in our simulation, because of the rigorous treatment and the material descriptiveness afforded by this method. Specifically, we wish to apply a recent hierarchical multirate FE software architecture [4], 5] designed for surgical simulation. This architecture partitions the underlying volume into a sparse, linearly elastic parent mesh as well as one or more dense, possibly nonlinear child meshes. It then decouples the subregions in a manner analogous to the Norton equivalent in circuit analysis: for each subregion, parent or child, it expresses the other subregion(s) encountered at each node as one equivalent impedance and force. An FE system composed of a parent and n children, characterized by a relatively large stiffness matrix k, is then reduced to decoupled systems with significantly smaller stiffness matrices is, i = 1… n + 1, where is made up of the original subsystem k as well as the Norton equivalents for the subsystems j = 1 ··· n + 1, j ≠ i. Moreover, the child mesh coinciding with the virtual tool would typically be updated at a high frequency, in conjunction with a haptic-rate time interpolation scheme.

The implications of our objectives for anatomical meshing are as follows.

1. Assuming that we have a sufficiently descriptive patient-specific tissue map as input, such as that illustrated in Figure 2 [6], the meshing must be rigorously tissue-guided, with the proviso that, for the sake of the simulation, it may be allowable, even preferable from a computational standpoint, to consider some tissue boundaries together. Also, it must specifically account for critical tissues in order to penalize gestures that cause damage to them. In contrast, existing meshing methods have been demonstrated typically on imaging data consisting of 2-class problems (inner tissue and outer background), or tissues with topologically simple boundaries (e.g., topologically equivalent to a sphere) [7], [8], whereas our simulation requires a far more descriptive anatomical mesh.

2. The method must produce as few elements as possible, to limit the complexity of the real-time problem, while meeting our requirements for haptic, visual and constitutive realism. Therefore, mesh scale must be spatially flexible, to allow small elements near the surgical target, particularly if an endoscopic view is required, while producing significantly larger elements far away, thereby limiting the number of elements overall, and still maintaining the conformality of the mesh. The hierarchical multirate FE model described in reference [4] suggests a way of treating this mesh that alleviates adverse effects on the condition number of the system, provided that parent and child systems are not themselves too ill-conditioned.

3. The meshing must reflect the topology of the underlying tissue: if a tissue features one or more inner boundaries, as well as an outer boundary, these boundaries must be accounted for if the clinical and constitutive realism of the simulation requires it. Proceeding this way gives us the option of modeling the ventricles filled with corticospinal fluid, as opposed to viewing the brain as an uninvaginated solid, and also allows us to model sinuses of arbitrarily complex topology on a patient-specific basis. By the same token, we can experiment with a meshing that accounts for only the subset of the vasculature that immediately surrounds the structure of interest, and discount the rest.

4. Next, the method should afford both 2D and 3D elements, as some tissues are better modeled as collections of surface elements, such as the dura mater, thin cranial bones and vasculature (the latter might be simplified as a curvilinear element, were it not for the requirement that cutting through it should appear realistic and be appropriately penalized in our simulation), while others are inherently volumetric. Existing methods that are purely volumetric [7] suffer from their inability to model tissues that are inherently curviplanar: rather than use just a few shell elements that feature no short edges, they are condemned to using a needlessly large number of small tetrahedra or hexahedra to limit the proportion between the longest and shortest edge of each for numerical stability [9].

5. Finally, the meshing method must produce high-quality triangles and tetrahedra: within each 2D or 3D element the edges should be of near-equal length, as opposed to 1 or 2 edges being significantly shorter than the others, for the sake of rapid convergence of the FE method [9]. Also, wherever smooth anatomical boundaries are involved, the surface visible to the user should be continuous, except where surgical interaction invalidates this assumption. To do otherwise is potentially confusing, from a visual and haptic realism standpoint. Existing methods can also achieve continuous surfaces as well as high-quality triangles [10], but have not yet demonstrated a mesh scale strategy sufficiently flexible to meet our endoscopic simulation requirements.

Figure 2. Tissue map computation from CT and MR, exploiting the tubular structure of critical tissues and the embedded structure of other soft tissues (from reference [6]). [Color version available online.]

The goal of the surface meshing procedure is to establish the topologically faithful tissue surfaces bounding each class or contiguous subset of classes, where each surface mesh exhibits the required edge scale pattern. Given our objectives, we have opted for a surface-model-based approach to tessellating anatomical boundaries, featuring the well-known simplex model [11], illustrated in Figure 3a. Its topological operators, specifically the Eulerian T₁ and T₂, as illustrated in Figure 3b, as well as the edge swap T₇ [11], provide explicit control over individual faces and edges. This surface meshing stage is followed by a tetrahedralization stage that also meets our mesh scale objectives and that uses as input the triangular boundaries produced by the surface meshing stage.

Figure 3. Tissue-guided simplex models: (a) 2-simplex mesh and dual triangulation; (b) T₁ and T₂ Eulerian operators defined on 2-simplex mesh. Prior results [19]: (c) radially varying simplex and (d) dual triangulated surface, topologically equivalent to a sphere. This topological limitation is addressed in the current paper. [Color version available online.]

Topologically accurate tissue-guided simplex meshing with spatially varying edge scale

As shown in Figure 3a, the m-simplex mesh (black) is a discrete active surface model [11], characterized by each vertex being linked to each of m + 1 neighbors by an edge. A surface model in 3D is realized as a 2-simplex, where each vertex has 3 neighbors, and this representation is the dual graph of a triangulated surface (blue), with each simplex vertex coinciding with a center, and each simplex edge being bisected by an edge, of a triangle. A balloon force can act on this mesh to cause it to expand until some image-based force halts this expansion. Furthermore, this surface model also features other internal forces [11] that nudge each simplex face, and consequently each dual triangle, towards having edges of equal or locally consistent length, and towards , or continuity, for example. The edge scale can be constant, within some tolerance, or spatially varying as in Figure 3c, consistent with a decomposition into parent (in white) and child (blue) subsystems, and leading to a triangulated surface of comparable scale. Finally, as shown in Figure 3c, our on-going research also deals with minimally supervised methods for computing a tissue map, accounting in particular for critical tissues and making use of spatial constraints such as the locally tubular structure of vasculature and cranial nerves, the embedded structure of soft tissues in relation to bone and air, and the contiguity of tissues in general.

This model has been limited by its topological equivalence with a sphere, in the absence of topological adaptivity. While topological adaptivity is achievable, based on operators published in reference [11], the convergence of the surface to the intended boundary, involving hundreds of iterations of a model integrating internal and image forces, is fraught with local extrema, a situation exacerbated by the capability of splitting or fusing. To alleviate this issue, we instead initialize the simplex model with a dense surface mesh of high accuracy and topological fidelity, resulting from Marching Cubes (MC) [12], based on the duality between a triangular surface and a 2-simplex mesh. We start from a densely triangulated surface produced by Marching Cubes, post-processed by an existing, topology-preserving, decimation method [13], which is somewhat more computationally efficient than ours, in order to reduce the number of triangles to a manageable number, as well as with identification and area-thresholding of contiguous structures, all VTK-based [14]. We then decimate the simplex mesh in a highly controlled, spatially varying manner, which we endow with topological adaptivity and explicit control over mesh scale, while exploiting a previously computed tissue map to guide the model on a tissue-specific basis. The final simplex boundaries can be converted to triangulated surfaces by duality.

This way of proceeding allows us more control over the decimation than existing algorithms that are not based on surface models, as our spatially varying control over mesh scale allows us to resolve the relevant anatomical surfaces densely enough for endoscopic simulation, while still limiting the number of triangles and tetrahedra sufficiently to make real-time interaction feasible. Control over mesh size is typically implemented through the T₁ and T₂ operators, as triggered by geometric measurements of each simplex face or edge. For example, if the smallest edge of a face is smaller than the edge scale objective at that position, to produce a sparser mesh we delete that edge by a T₁ operation. (The T₁ operation actually replaces 5 edges with 2, so it is permissible to target one of the edges adjacent to the intended edge if this leads to a better fusion of two faces, e.g., one that involves a smaller angle between the normals of the two faces fused, or one that produces a less elongated new face.) Also, if a simplex face has more than k vertices (k = 7 usually), coinciding with a triangular mesh vertex with more than k incident, typically elongated, triangles, we also use T₁ and T₂ to reduce the number of simplex vertices and improve surface mesh quality.

It should also be emphasized that our procedure identifies anatomical surfaces prior to volumetric meshing, rather than proceeding directly from the classification to tissue-guided volumetric meshing, because some tissues are inherently curviplanar rather than volumetric and are more efficiently modeled by shell elements than tetrahedra or hexahedra. Also, a purely volumetric approach will generally not produce a mesh that is as smooth and that closely agrees with the anatomical boundary: from a haptic and visual rendering standpoint, an anatomical model with jagged or badly localized boundaries would detract from the realism and clinical relevance of a surgical simulator, in addition to confusing the user.

This stage produces a set of triangulated surfaces that we convert to simplex meshes by duality. From geometric tests to ascertain the shortest edge of each face, we iteratively perform T₁ operations on those faces whose shortest edges are furthest from their respective objective. We use heap-sorting to fix the “worst” edge first. We note that when the curvature of the boundary is sufficiently pronounced, with respect to the edge scale objective, T₁ operations lead to faces whose center lies too far from the boundary (only the vertices of each face are attracted to the boundary by image forces). At that point, the optimal representation may be a trade-off between the desired edge scale and the desired proximity of the face center to the boundary (a parameter). This trade-off entails the recruitment of T₂ operators to partition each ill-fitting face into two.

Spatially varying edge scale strategies: radial and surgical path-based distance

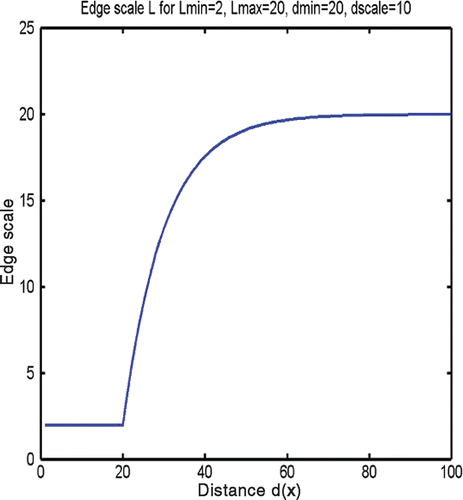
As demonstrated in Figure 3, control over simplex mesh edge scale can be exercised with a radially varying surface mesh scale function . This function is defined at any x in the volume spanned by the mesh, based on the Euclidian distance from a user-provided central point p_c (e.g., on the pituitary gland). For example, we define

where and specify the smallest and largest edge scales of the simplex mesh, and d_min andd_scale determine the behavior of the function bridging the two values: an exponential function of the distance from the midpoint x_m,ei of the edge e_i to the central point, p_c. This scale function, illustrated assuming typical parameters in Figure 4, thereby produces consistently small edges near the pituitary gland and, beyond a transition whose abruptness is controlled by the parameter d_scale, longer edges away from it.

Figure 4. Edge scale function, assuming typical parameter values.

Alternately, we can also enforce a face area function, which can be derived from the edge scale, based on the duality with regularly triangulated data. Assuming an ideal of near-equilateral triangles, a triangular face area scale is related to an edge length scale by . After some manipulation, where by duality the number of faces is related by and [11], we have a simplex face-area to edge-length relationship . Also, more than one child is possible, at the cost of selecting other “central” points of interest x_c,i, in which case we define .

For anatomical meshing cases that require dense meshing in an elongated volume near an intended surgical path, rather than a spherical volume, we can alternately specify at any x a surgical path-based mesh scale function , substituting d_SP for d_R in expression (1), where S = {E_i(p_i, p_i + 1)} is a set of linear edges E_i. Each edge E_i connects two user-provided points p_i and p_i + 1, and together they approximate an intended surgical path:where u, v ∈ [0, 1] [15]. This expression defines the minimum distance from x to the set of edges S that is a linearized approximation of the intended surgical path.

This notion of using proximity to a point or to an intended surgical path to optimize mesh size can be extended to choices about constitutive and clinical realism. For example, within a distance threshold ε_d from a point or a path, we may elect to model soft tissues as nonlinearly elastic, beyond which we are content with linearly elastic behavior. The distance threshold need not be constant along a path: if, for example, we had to model a cranial procedure, as the inwards arclength s of the path increases, ε_d(s) would tend to be larger at the surface (s = 0) and become smaller along the path. Or, for any x where d_SP (x, S) > ε_d, we may model skin, muscle, fat and bone as having a prescribed null displacement, thereby effectively eliminating them from the real-time FE problem, whereas closer to the surgical path, we can account for the material properties of mucosa, muscle and even bones, as in the case of the sphenoidal sinus. Finally, far away from the path, it is expedient to not account for critical tissues, which can be obtained based on processing of MRI data with the method described in reference [6] and of MRA data with a method such as that described in reference [16], as this subset of critical tissues is less relevant to the simulation and otherwise would only add to computational overhead.

Almost-regular volumetric meshing with spatially varying resolution control

The last stage in our procedure partitions each volume bounded by a triangulated mesh, coinciding with a tissue class or contiguous subset of tissue classes, into tetrahedral elements consistent with the FE method. The volumetric meshing stage is based on a technique published by Fuchs [17] that automatically produces an optimal tetrahedralization from a given polygonal boundary, such as a triangulated surface. In this case, optimality is defined as near-equal length of the tetrahedral edges, along with a sharing of each inner vertex by a nearly consistent number of edges and tetrahedra.

This method features the optimal positioning of inner vertices followed by a Delaunay tetrahedralization. The resulting near-regularity is important for FE stability and efficiency [9]. More importantly, and in keeping with the philosophy of our method, vertex positioning is governed by a prescribed density function ρ(x), which can be spatially varying and correlates with the edge length objective pursued so far.

The positioning of vertices is divided into two stages:

• Construction of an initial configuration of vertices, based on the notion of a canonical tetrahedron, and in accordance with the specified density function ρ(x);

• Adjustment of vertex positions by minimization of a penalty functional.

A canonical tetrahedron leads to a partitioning of R³ with congruent tetrahedra, whose intersection is either empty, or a vertex, an edge, or a face. In addition, it is invariant under subdivision.

Ideally, tetrahedralization should be based on equilateral tetrahedra, but Fuchs argued that this shape does not permit a congruent partion of space. Nevertheless, near-regular elements are desirable for FE applications, which justified his investigation of almost-regular canonical tetrahedra. These conditions of congruence and subvision-invariance could be fulfilled through any one of 4 canonical shapes, with the final choice being the one that differs the least from an equilateral shape: a tetrahedron with canonical verticeswith x₁ set to 1/3. This shape has 4 dihedral angles of 60° and 2 of 90°, for an average of 70.53° and a standard deviation of 14.15°, as well as four edges of length 1 and two of length , for a standard deviation of 0.089 from the equilateral case. Each inner vertex should be shared by 24 tetrahedra.

Based on the relationship between the number of simplex and triangle vertices V_t ≈ V_sm/2 [11] and a corresponding target simplex mesh size of , the triangle or a tetrahedral mesh size works out to be . In summary, we modify the Fuchs tetrahedralization technique by specifying the target edge length based on a distance from each tetrahedral vertex to a point or to a linearized surgical path, depending on the requirements of the simulation. The separation of the resulting tetrahedral mesh into child and parent is as follows: contiguous tetrahedra whose edge lengths approach comprise the child mesh, while the other elements constitute the parent.

Results and discussion

Figures 5 and 6 contrast an existing, curvature-sensitive (but otherwise spatially consistent) decimation algorithm [13] with our spatially varying, simplex-based surface mesh decimation. Figure 5 displays a synthetic cube with 4 tubular openings through it, along axes x and y, to which we have added a synthetic hemispherical “gland” in its inner ceiling: Figure 5a shows the surface as originally identified by MC; Figure 5b shows it as decimated by the existing method. Its dual, featuring 1224 faces, initializes our spatially varying method, whose results are shown in Figure 5c, featuring 585 faces and dense faces on the gland, where edge color from white to fully saturated red indicates a tissue proximity varying between 0 and 3 mm, and whose dual triangulated surface appears in Figure 5d. We choose a proximity threshold that is tight at the gland and looser far away. A halt is triggered here by a near-constant number of faces, where scale-based T₁ and proximity-based T₂ operations offset each other. Figure 6 shows results for a brain surface, going from the prior method in Figure 6a to the results of our method in 6b and c. The graphs in Figure 6d illustrate the evolution in terms of the number of simplex faces and average distance to the tissue boundary: the reduction of the number of faces is traded off against proximity to the boundary, especially far from the area of surgical interaction. Here, T₁ and T₂ operations are applied every 3 iterations.

Figure 5. Contrasting decimation methods on a synthetic invaginated cube surface, featuring a hemispheric inner gland: (a) wireframe of MC results; (b) existing decimation method [13] displayed as a 3D wireframe overlaid on a surface rendering; (c) and (d) radially varying simplex mesh, featuring final simplex and dual triangular results. [Color version available online.]

Figure 6. Contrasting decimation methods on the brain surface: (a) the existing method, featuring a wireframe of the overall brain surface mesh and a closeup of the wireframe overlaid on the rendering of the brain surface, centered on the pituitary gland; (b) a radially varying simplex mesh, featuring wireframe and overlay closeup views as in (a); (c) a radially varying triangular surface, dual to the simplex mesh in (b). (d) Decimation statistics: (top) the number of faces, and (bottom) the average distance to the boundary plotted against simplex iteration, in going from the dual of (a) to (b) (2618 to 1051 faces). [Color version available online.]

Next, Figure 7 illustrates the flexibility and clinical applicability of the surface meshing method, in its ability to characterize relevant critical tissues, which are currently modeled as hollow and meshed at constant density. Blood vessels irrelevant to the simulation are not considered.

Figure 7. Clinically useful meshing: superposition of relevant critical tissue meshes with the brain surface. Basilar arteries and optic and oculomotor nerves are shown as triangular mesh. [Color version available online.]

Figure 8 depicts how a combination of path-based (ε_d,SP = 10 mm) and radial (ε_d,R = 25 mm) distance allows us to convert “distant” extra-cranial tissue to “null displacement” tissue to exclude it from the real-time biomechanical problem. These two distances are then used to determine the mesh scale.

Figure 8. The use of radial and path-based distance to convert “distant” extra-cranial soft tissue to tissue of null displacement and determine edge scale: (a) original tissue map [6]; (b) null-displacement tissue (in orange); (c) final wireframe and rendering of triangulated surface, with dense results visible within 10 mm of the path. [Color version available online.]

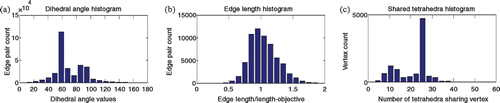
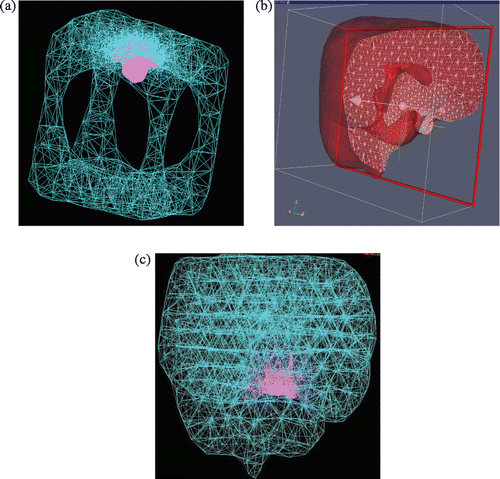
Finally, Figures 9 and 10 illustrate our topologically accurate, radially varying tetrahedralization. Figure 9 illustrates typical results on the cube and brain volumes. The former meshing is visualized as a wireframe composed of all tetrahedral edges. The brain tetrahedral meshing is shown as a semi-transparent volume whose intersection with a clipping plane is shown as a set of triangles, as well as a wiremesh of all edges in a manner comparable to the cube. Figure 10 provides statistics from the brain tetrahedralization, in the form of histograms of dihedral angles of edge pairs, edge lengths in relation to spatially varying edge length objectives, and the number of tetrahedra shared by each vertex. As expected, the dihedral angles have a large mode at 60° and a smaller mode at 90°, the edge length/length-objective statistic is peaked at 1.0, and the histogram expressing number of shared tetrahedra per vertex has two modes: a large one at 24, and a smaller one at 12, coinciding with boundary vertices.

Figure 9. Topologically accurate, radially varying brain volume tetrahedralization: (a) invaginated cube visualized as 3D wireframe of all tetrahedral edges, with child mesh in pink and parent mesh in turquoise; (b) brain mesh visualized as semi-transparent boundary of clipped volume, where triangular intersections of tetrahedra with the clipping plane are shown as a white wireframe; and (c) brain mesh visualized as a 3D wireframe rendering.

Figure 10. Distributions of (a) dihedral angles of edge pairs, (b) edge length over length-objective, and (c) number of shared tetrahedra for each vertex.

Conclusions

This paper presented a new meshing strategy for computing patient-specific anatomical models comprised of triangles and tetrahedra coinciding with, or for computational efficiency idealized as, homogeneous tissue, in a manner that addresses the requirements of endoscopic pituitary surgery simulation. Our surface mesh method combines the strengths of Marching Cubes and the simplex mesh model for computing triangulated boundaries, in terms of topological fidelity and control of mesh characteristics such as edge scale. While each method on its own is well researched, the combination of the two, and in particular the edge scale strategy, is novel. Our strategy offers promise for dealing with the conflicting requirements of narrowly focused, and especially endoscopic, visualization and haptic rendering, as well as the computation of body forces and displacements over large volumes, particularly if combined with hierarchical multirate finite elements. Our notion of edge scale extends flexibly to decisions about constitutive and clinical realism, such as which subset of tissues to consider as having null displacement. This method is conceived to be extensible to surgery simulation in general, and appears able to deal with any tissue shape as well as most practical requirements for tissue mesh size. In short, it offers promise as a meshing stage for computing anatomical models for medical simulation, and eventually for constitutively realistic, patient-specific surgical planning.

In the near future, the particular choice of parameters for our application will be settled in conjunction with improvements to the prior tissue classification and with the application of HMFEs to our models. We will also investigate a conformality-preserving simplex force, which would cause two contiguous boundaries to share vertices wherever desirable. A more thorough validation of these methods will follow, based on a refinement of the MNI digital head phantom [18] to account for bone and critical tissues.