Finite element analysis of an elastic model of the brain: Distortion due to acute epidural hematoma–the role of the intra-ventricular pressure gradient

Abstract

Introduction: Recent studies on biomechanical properties of brain tissue have focused on computer simulation of this tissue during impacts, simulation of neurosurgical procedures, and improvements in navigational systems for image guided surgery. Several models have been proposed to explain the mechanical behavior of brain tissue in different conditions (dynamic, static and quasi-static), but the role of the ventricles and intra-ventricular pressure has not been studied so much, especially under static loading. It is clear that the ability of biomechanical models to predict the displacement of midline structures secondary to epidural hematoma could effectively improve the accuracy of intra-operative navigational systems. In addition, simulation of midline shift can help us to understand the mechanisms involved in pathogenesis of these conditions. Plain strain computer modeling based on finite element methods has been used to study the degree of displacement and deformation of the ventricles in acute epidural hematoma to determine the more important factors in achieving a more accurate model.

Materials and Methods: A patient with an acute epidural hematoma was used to produce a plain strain elastic model of brain tissue. The model was based on the CT data. The displacement of reference points in the modeled ventricle with changing intra-ventricular pressure gradients was compared with the displacement of similar points in the real ventricle as calculated from the CT scan, and the pressure gradients that resulted in the minimum error were determined.

Results: Our data showed that best results were achieved when the pressure gradient was 1.25 KPa (9.4 mm Hg). Also, the ventricle ipsilateral to the hematoma was predicted to be compressed from both the medial and lateral walls.

Conclusion: In the plain strain biomechanical modeling of the brain in unilateral strain loading (conditions similar to those used in image guided systems), the intra-ventricular pressure gradients should be considered in order to achieve accurate results. In addition, the so-called “strain shadow effect” is emphasized.

• Brain modeling
• elastic
• finite element
• epidural hematoma
• intra-ventricular pressure

Introduction

The biomechanical behavior of brain tissue has been one of the most problematic and controversial modeling issues [1–5]. The earliest modeling systems employed were impact models [4], [7–9]; these were soon followed by animal studies with static, quasi-static, and dynamic biomechanical models. With the introduction of neuronavigation, image registration systems and robotic neurosurgery, enthusiasm for brain modeling became more pronounced [8], [10–16].

Prediction of the magnitude of final displacement of the midline structures has been an important problem in brain modeling. Many studies performed on animals have been published, though their relevance and applicability to humans may be a matter of dispute [8]. Despite their limited availability, cost and complexity, intra-operative imaging systems yielding precise images have brought about alternative solutions, the most important being the ability to update pre-operative data with biomechanical modeling of brain displacement [17], [18].

Epidural hematoma is a classic and familiar condition that enables neurosurgeons to correlate the effects of an acute unilateral cortical displacement with the shift of midline structures. It has the advantage of not confronting interstitial tissue parameter changes, as commonly seen with subdural and intra-cerebral clots.

As most of the intra-operative displacements occur in the superficial layers, these systems are concerned more with cortex [18]. It has also been suggested that placing fiducials near the ventricle may be a source of error [11].

In this study employing a plain strain biomechanical model of the brain, taking into account the role of the intra-ventricular pressure gradient, the displacements of midline structures have been calculated and compared to actual findings.

Material and methods

A 31-year-old man with a 35-mm-thick left temporoparietal epidural hematoma three hours after sustaining blunt head injury was used as the main model. There was no evidence of associated edema or contusion on his CT scan (Figure 1).

Figure 1. Patient's CT scan with left parietal epidural hematoma. Note the midline shift; the imaging is otherwise normal.

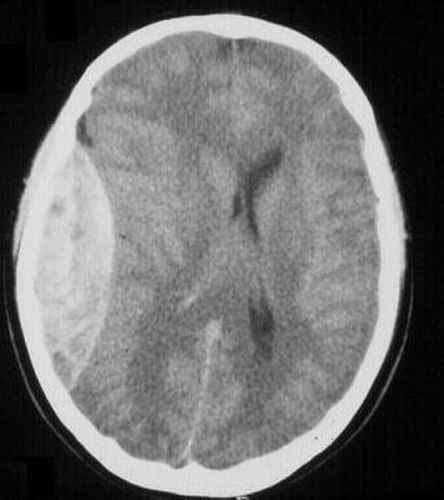
A control CT scan was performed 3 months later after successful treatment of the patient to estimate normal ventricular size and position.

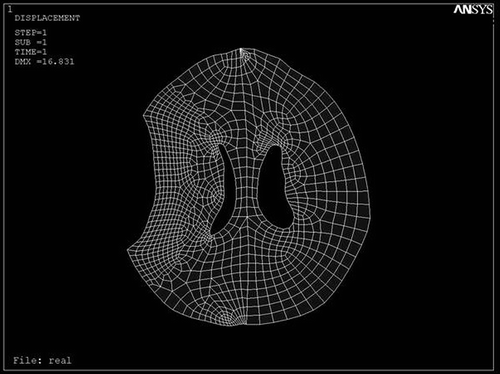
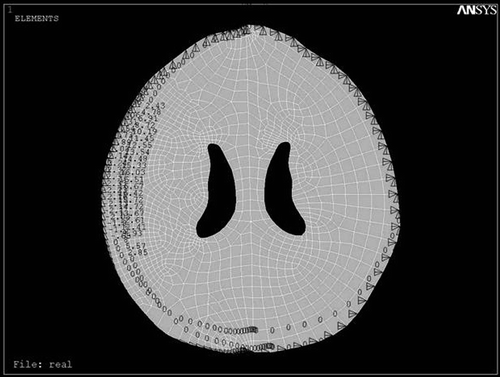
The patient had a Glasgow Coma Scale score of 12 and the CT scan was performed parallel to the orbito-meatal plane with slices 10 mm apart. The corresponding DICOM file was obtained and visualized by Acculite DICOM viewer software. The outlines were defined in the modeling software (Mechanical Desktop Version 2004), then the geometric model was constructed in the mechanical analysis software (CATIA 5R 11). Meshing was performed with ANSYS 8.0 software and refined in the vicinity of the hematoma. The boundary conditions for the hematoma perimeter, internal calvarial surface, and interior of the ventricle were defined, then strain loading was applied (Figure 2).

Figure 2. Biomechanical modeling of the CT data after meshing and applying boundary conditions in ANSYS 8.0. Note the refinement in the vicinity of the load.

Assuming brain parenchyma to be homogenous and isotropic with material parameters E = 10, ν = 0.45 (Young modulus and Poisson ratio, respectively) [19], the predicted midline shift was recorded. The results obtained were compared quantitatively to baseline values deduced from the brain CT scan acquired 3 months later (i.e., without the hematoma), and the ventricular shape was compared qualitatively.

Results

In the CATIA software, the ventricular border of the loaded model was marked by 15 reference points (Figure 4), and the shifts were calculated by comparison with the delayed CT scan of the patient after 3 months.

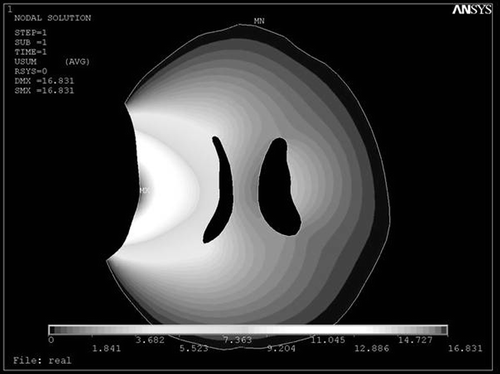
Figure 3. Displacement field of modeled brain after loading the displacements of the hematoma with intra-ventricular pressure of 1.25 kPa in ANSYS 8.0.

Figure 4. Nodal solution of the modeled brain with p = 1.25 kPa in ANSYS 8.0.

The effect of the ventricular pressure difference was calculated at different values (0–1.5 Kpa in steps of 0.25 KPa) for each ventricle (Tables I and II). Employing the least-square method for displacement of 15 reference points, the error magnitude was estimated (Table III).

Table I.  The difference (d) between displacement of reference points on the modeled brain and the patient's left ventricle with different pressure gradients (P = intra-ventricular pressure in kPa; D = displacement).

P
D	P = 0.25	P = 0.50	P = 0.75	P = 1.00	P = 1.25	P = 1.50
d1	3.47	2.83	2.93	3.06	2.78	3.00
d2	2.67	2.43	2.45	2.62	2.71	3.01
d3	2.61	2.28	2.46	2.68	2.72	2.95
d4	1.80	1.78	2.00	2.22	1.91	2.24
d5	1.14	1.28	1.58	1.51	1.69	1.82
d6	0.82	1.29	1.39	1.35	1.57	1.75
d7	1.14	1.63	1.86	2.08	2.34	2.50
d8	1.74	2.20	2.36	2.55	2.96	3.03
d9	4.90	4.16	3.79	3.35	3.12	2.94
d10	6.10	5.13	4.47	3.87	3.18	2.69
d11	6.00	5.15	4.33	3.61	2.78	2.14
d12	5.36	4.85	4.08	3.22	2.84	1.89
d13	5.45	4.74	3.91	3.37	2.46	2.45
d14	5.19	4.59	3.87	3.42	2.82	1.97
d15	4.72	4.41	3.59	2.96	2.76	2.05

Table II.  The difference (d) between displacement of reference points on the modeled brain and the patient's right ventricle with different pressure gradients (P = intra-ventricular pressure in kPa; D = displacement).

P
D	P = 0.25	P = 0.50	P = 0.75	P = 1.00	P = 1.25	P = 1.50
d1	0.76	1.24	1.04	1.53	1.39	1.66
d2	1.13	1.41	1.93	1.33	2.92	3.52
d3	1.02	1.29	1.80	1.22	3.17	3.66
d4	0.95	1.36	2.06	1.19	3.16	4.11
d5	0.64	1.40	1.88	0.78	3.43	4.12
d6	0.65	1.39	1.68	0.67	3.31	3.84
d7	0.77	1.02	1.09	1.02	1.74	2.01
d8	1.57	1.51	1.26	1.11	1.62	1.37
d9	1.59	1.41	1.13	1.55	1.62	1.72
d10	1.63	1.36	1.23	2.77	1.08	0.96
d11	1.67	1.55	1.23	2.83	0.82	0.66
d12	1.63	1.28	1.08	2.88	0.74	0.75
d13	1.61	1.41	1.18	2.63	0.86	0.84
d14	1.49	1.52	0.92	2.48	0.90	1.11
d15	1.34	1.41	1.01	1.71	1.16	1.49

Table III.  The mean square value of differences in the displacements of reference points of the modeled ventricle and the patient's ventricles with different pressure gradients (P = intra-ventricular pressure in kPa).

Σdi⁁2/n
P	Right ventricle	Left ventricle
P = 0.25	1.66	16.03
P = 0.5	1.89	12.54
P = 0.75	2.02	10.07
P = 1.00	3.51	8.31
P = 1.25	4.45	6.86
P = 1.50	6.14	5.00

Our results revealed that the least relative error for both ventricles could be obtained when Δp = 1.25 Kpa. Also, the predicted ventricular shape and shift were compared qualitatively with the patient's CT scan. As shown in Figure 3, the ipsilateral ventricle is compressed from both medial and lateral surfaces, and a “strain shadow” is actually spread over the contralateral hemisphere.

Discussion

Investigation into the mechanical properties of very soft tissues like brain has been the focus of recent efforts [14]. Traditionally, development of epidural hematomas has been known to cause brain deformity and ventricular shift. The magnitude of this displacement, as well as the extent of ventricular collapse, is a function of tissue parameters (Poisson ratio and Young modulus), compensatory mechanisms, and hematoma volume.

The tissue parameters may change during craniotomy due to the effect of anesthetic agents, mannitol, and hyperventilation. In our patient, however, the parameters were close to those of normal brain under the same regimen.

Gray and white matter, as well as basal ganglia, have been differentiated in various studies; however, the net effect of this dichotomy has not been addressed by other authors [9], [18], [20]. Therefore, we have assumed the brain to be homogenous and isotropic, and have neglected the effect of basal ganglia and corona radiata on focal material parameters.

As can be seen in Figure 3, the strain field is concentrated around the medial and lateral surfaces of the ipsilateral ventricle to collapse it. This “strain shadow” effect protects the contralateral hemisphere from disturbance, and may be attributed to the particular geometry of the ventricle.

Intra-ventricular pressure theoretically and mechanically defines the boundary condition of the ventricle in our model. This pressure increases with increasing hematoma volume, and this effect in turn prevents premature collapse of the ipsilateral ventricle (Figure 3). Also, the “strain shadow effect” of the ipsilateral ventricle leads to relatively larger size for the contralateral ventricle.

Some workers have defined sub-domains for basal ganglia and the internal capsule with specific tissue parameters. Although the results obtained with such models are more precise, they require approximately 35 hours to be processed [11], while our method takes less than 15 minutes to obtain the final results. Employing mesh-warping algorithms would also be easier with our method.

In conclusion, it seems that elastic homogenous and isotropic modeling for acute brain distortion is safe, keeping the error level within an acceptable range, and that the material parameters are close to normal brain values. It is also noted that ipsilateral intra-ventricular pressure determines the final shape of the ventricles.