Evaluation of a computerized measurement technique for joint alignment before and during periacetabular osteotomy

Abstract

Periacetabular osteotomy (PAO) is intended to treat a painful dysplastic hip. Manual radiological angle measurements are used to diagnose dysplasia and to define regions of insufficient femoral head coverage for planning PAO. No method has yet been described that recalculates radiological angles as the acetabular bone fragment is reoriented. In this study, we propose a technique for computationally measuring the radiological angles from a joint contact surface model segmented from CT-scan data. Using oblique image slices, we selected the lateral and medial edge of the acetabulum lunate to form a closed, continuous, 3D curve. The joint surface is generated by interpolating the curve, and the radiological angles are measured directly using the 3D surface. This technique was evaluated using CT data for both normal and dysplastic hips. Manual measurements made by three independent observers showed minor discrepancies between the manual observations and the computerized technique. Inter-observer error (mean difference ± standard deviation) was 0.04 ± 3.53° for Observer 1; −0.46 ± 3.13° for Observer 2; and 0.42 ± 2.73° for Observer 3. The measurement error for the proposed computer method was −1.30 ± 3.30°. The computerized technique demonstrates sufficient accuracy compared to manual techniques, making it suitable for planning and intraoperative evaluation of radiological metrics for periacetabular osteotomy.

• Periacetabular osteotomy
• inter-observer error
• radiographic angles
• preoperative planning
• acetabular coverage
• cartilage segmentation

Introduction

Developmental dysplasia of the hip (DDH) commonly leads to early arthritis and the need for hip replacement. If DDH is diagnosed before degenerative changes have occurred, the hip joint of younger adults (less than ∼ 55 years old) can be realigned surgically using a technique called periacetabular osteotomy (PAO) [1], [2]. The PAO attempts to restore the abduction, flexion, and version of the acetabulum to provide optimum coverage of the femoral head [3]. Reorientation evenly distributes stresses through the hip joint during weight bearing, lessens pain, and reduces the risk of future arthritis. Surgeons typically use measurements from radiographs [4–6] to diagnose DDH and to correctly reorient the acetabulum during PAO. Computed tomography (CT) offers the advantage of characterizing the three-dimensional (3D) abnormal anatomy. Methods for preoperatively planning of PAO include CT-based surface rendering and coverage area [7–10], biomechanical estimations of contact pressures within the joint [11–14], and angular measurements of acetabular coverage of the femur on reformatted CT slices [15–18].

Angular measurements used to describe the acetabulum include the Center-Edge (CE) angle of Wib [4], [16], the Acetabular Index (AC) indicating the obliquity of the sourcil [19], the Superior-Anterior coverage (S-AC) angl [18], [20], and the Acetabular Anteversion (AcetAV)[7], [21], [22]. These manually measured angles indicate deficient coverage due to DDH compared to normal values[18], [20], [23], and are the basis for planning the PAO surgery. There is currently no method by which these angles can be updated as the acetabular fragment moves. Because the radiographic angles are measured according to the irregular bony anatomy of the acetabulum, which is moving with respect to the patient's anatomical axes during realignment, only a limited correlation exists between the true rotation of the acetabular fragment and the preoperative surgical aims for the radiographic angles.

During PAO, the surgeon reorients the acetabular bone fragment using apparent anatomical landmarks or by fixing references (e.g., Kirschner wires [11]) to the pelvis and fragment to measure relative motion. An AP fluoroscopic radiograph of the hip is checked intraoperatively to assess the position of the fragment before securing it with screw fixation. Positioning the acetabular fragment during PAO is difficult even for experienced surgeons, and the 3D nature of the hip deformity adds to this difficulty. A computerized system that can template corrections to the radiological angles using CT scans and provide intraoperative verification with a navigation system has the potential to greatly enhance the surgeon's ability to achieve reproducibly the preoperative aims of the osteotomy [11]. This paper reports the development of a unique computational algorithm, called the Lunate-Trace method, for measuring the radiological angles commonly used to assess hip joint coverage in real time, and compares the accuracy of this method to manual angle measurement.

Materials and methods

Patients

To evaluate the accuracy with which the Lunate-Trace algorithm measures radiological angles, CT scans were evaluated from two patient groups. The first group included 12 consecutive patients who underwent PAO as a result of symptomatic hip dysplasia, and the second group included 12 patients without signs of dysplasia that had previously undergone an investigative CT scan for other reasons (e.g., trauma or tumors) unrelated to osteoarthritis or structural anomalies. Institutional review board approval was obtained for this study. In accordance with current clinical protocols, patients with dysplasia underwent CT scans both before and at a minimum of 16 weeks after PAO [20]. Thus, three sets of CT data (12 dysplastic preoperative PAO, 12 postoperative PAO, and 12 normal hips) were available for measurement and analysis.

Patients were scanned supine from approximately 4 cm superior to the hip joint to 6 cm inferior. At the time of scanning, the radiologist took care to align the patient's midline with that of the CT table in order to obtain true transverse slices of the femoral heads. Anatomical landmarks including the superior aspect of the pubic symphysis and the coccyx apex were visible within the scanned volume. Original scan formats varied, but the median voxel dimensions were 0.684 × 0.684 × 2 mm (xy range: 0.625 to 0.938 mm; z range: 0.5 to 4 mm).

Manual measurement of radiological angles

Three trained observers independently measured the radiological angles from CT data using conventional techniques. These observers comprised an attending musculoskeletal radiologist (K.T. – Observer 1), an attending orthopaedic surgeon (S.C.M. – Observer 2), and a biomedical engineer (R.S.A. – Observer 3) with knowledge of the bony anatomy of the pelvis and an understanding of the definitions of the characteristic angles used in this study. The observers independently selected points on CT image slices in sagittal, coronal, or transverse views. Each observer selected the anatomical landmarks, including the femoral head centers, as points. For angular calculations, line segments were drawn between the appropriate points and the measurement was automatically calculated. The observers either confirmed or repeated the selections before saving the data digitally.

Each observer measured and recorded the four angles characterizing the acetabular coverage of the femur (CE, AC, S-AC, AcetAV) unilaterally on a patient-specific basis. During measuring, the observer first selected the center point of the femoral head using crosshairs controlled by a computer mouse. The center point defined the coronal, sagittal, and transverse slices used to measure subsequent angles. The second task was to measure each of the four angles (Figure 1.) using enlarged, full-screen views of the reformatted CT slices.

Figure 1. All angles were measured from the three reformatted CT slices (coronal, sagittal, and transverse) passing through the center of the femoral head on the ipsilateral side. In the coronal view, the CE angle and the AC angle were measured. The CE angle is defined by the most lateral aspect of the acetabular rim, the center of the femoral head, and a point vertical (superior) to the center point. The AC angle measures the obliqueness of the acetabular roof based on the most lateral and the most medial aspects of the sourcil, and a horizontal (lateral) line. The S-AC angle and the AcetAV are measured from image reformats in the sagittal and transverse planes, respectively. In the sagittal plane, the most anterior portion of the acetabular rim, the top of the acetabular roof, and a horizontal line make the S-AC angle. The acute AcetAV angle is measured by a line parallel to the acetabular opening and one perpendicular to the centers of the femoral heads on the transverse plane. [Color version available online.]

Computerized measurement method

Using MATLAB® (Mathworks, Natick, MA), we designed a custom computer application named Lunate-Trace, which allows the user to load CT data in DICOM format into a software environment, segment the acetabulum lunate, and automatically measure radiological angles. User input is required only to trace the outline of the joint from CT data. After segmenting the joint surface, the application automatically measures the radiological angles directly from the 3D surface approximation of the acetabulum lunate (Figure 2.).

Figure 2. The oblique slicing method for segmenting the acetabulum lunate. A) Reformatting CT slices are acquired circumferentially about the medial-lateral joint line. This allows the lunate to be traced using the two intersections (medial, lateral) on each slice. B) The creation of the parametric surface implements an oblique plane (blue) rotated about the medial-lateral axis of the joint to find and interpolate points. The acetabulum of this right hip is viewed from the posterior-lateral direction. [Color version available online.]

Outlining the acetabulum lunate. The acetabulum lunate segmentation process began with bilateral selection of the femoral head center to define a reference axis in the medial-lateral direction (inter-capital line). Image-processing algorithms automatically cropped the data to a single cubic subvolume (72 mm on each side) centered about the ipsilateral joint center. The algorithm next resampled the volume using cubic interpolation, yielding voxels of uniform cubic dimensions (edge-length 0.6 mm). Oblique CT image slices were taken circumferentially about the medial-lateral axis of the joint at 7.5° increments.

Using the oblique image slices, the user traced first the lateral and then the medial edge of the lunate surface by selecting the boundary points of the subchondral bone sequentially on each slice. The selected points bound a closed 3D curve (3^rd order polynomial spline) which defined the continuous margin of the acetabulum lunate. Approximately 75 points spaced approximately 3.5 mm apart were required to complete the trace. A cubic-spline smoothing algorithm was applied to reduce non-physiological regions of high curvature. To describe the interior load-bearing surface of the joint, we interpolated the radius of curvature of the hip joint between the medial edge and lateral rim of the lunate surface at fixed intervals. Using this method, we avoided making a spherical assumption about the joint and more closely matched the contour of the dysplastic hip. The interpolated vertices were then tessellated with triangular faces to form a continuous, curved surface describing the boundary and contact region of the hip joint.

Radiological angle calculation

We developed the Lunate-Trace algorithm to solve instantly radiological angles using the 3D model of the hip joint. The CE and AC angles were measured by first calculating the intersection between the 3D curve and the coronal plane defined at the femoral head center. Using the intersection points, each angle was calculated using methods analogous to the image-based angle definitions (Figure 3.). Similarly, the algorithm measured the AcetAV angle using the intersections of the lateral trace of the lunate outline with the transverse plane.

Figure 3. Transparent views of the acetabulum. The 3D Lunate-Trace curve is shown as a blue outline, and the region in red is the interpolated surface of the acetabulum lunate. The angles are defined using the segmented model, and are analogous to those in Figure 1. [Color version available online.]

The calculation of the S-AC angle differed slightly from that of the other three angles because one of the defining points is the most superior aspect of the acetabulum on a sagittal plane. This point was not part of the 3D curve, but rather lay on the interpolated surface. The computer algorithm calculated the superior roof of the acetabulum by first creating a vertical ray originating from the femoral head center. The intersection of this ray with the contact surface was solved mathematically in a method know as ray firing. The most superior aspect of the joint was used with the anterior intersection of the 3D curve on the sagittal plane to calculate the S-AC angle.

Determining the center of acetabular curvature

Due to the increased slope of the acetabulum and insufficient coverage associated with DDH, the femoral head may subluxate (move) upwards and laterally, and therefore the femoral and acetabular centers may not coincide. To investigate this effect, the points selected by the user for tracing the acetabulum lunate were used to calculate the acetabular curvature independent of the femoral head center. We used a least-squares spherical fit of the 3D trace-points to solve the center of curvature of the acetabulum. The solved acetabular center point was then compared vectorally to the manual observer selection of the femoral head center. A discrepancy in these two points would justify the use of CT image data rather than 2D radiographic extrapolation of the 3D joint contact surface, because the 2D algorithms rely on an assumption of spherical hip joint congruity to resolve the third Cartesian dimension of points defining the acetabulum [10], [24–26].

Data analysis

Statistical analysis was used to identify the sources and extent of possible error in the computerized model. Due to the varying individual morphology of the patients, the angle measurements were expected to vary widely. Therefore, to compare the data between observers and methods, we used the mean results of the three manual observers as a control observation group. The differences between each recorded measurement and the control measurements were studied to highlight discrepancies between observers and to evaluate the computer technique. In this study, the term “error” refers to the difference between any measurement and the corresponding value of the control set. A one-way analysis of variance (ANOVA) was used to test for a significant difference (p < 0.05) between techniques. Additionally, we divided the measurements into groups to identify factors that might contribute more to the individual measurement error. These groups were based on angle type (CE, AC, S-AC, AcetAV) and patient type (Dysplastic PreOp, Dysplastic PostOp, Normal). Post-hoc multiple comparisons of means based on the ANOVA results were also performed with the Tukey honestly significant difference (HSD) criterion using MATLAB® (Statistics Toolbox, Mathworks, Natick, MA).

Results

Inter-observer measuring error

The computerized Lunate-Trace technique for measuring radiological angles was evaluated for accuracy first by comparing all recorded measurements for all three groups of patients to the corresponding values in the control data set. Table I. shows the complete list of angle measurements by each of the observers and the Lunate-Trace method for the 12 preoperative dysplastic cases, 12 corresponding postoperative dysplastic cases, and 12 normal cases. Three observations (marked –) are not recorded because the angle was undefined (i.e., at least one of the anatomical features required for angle calculation was not visible on the chosen slice plane due to variations in morphology).

Table I.  Recorded radiological angle measurements (in degrees) for manual observers (O1–O3) and the computerized Lunate-Trace method (LT) for a total of 24 patients (Pt). A (−) entry indicates that no measurement was recorded because the required anatomical features were not visible on the slice plane.

	Dysplastic - PreOp					Dysplastic - PostOp					Normal
Angle	Pt	O1	O2	O3	LT	Pt	O1	O2	O3	LT	Pt	O1	O2	O3	LT
CE	1	14	15	23.4	20.5	1	29	25.8	28.9	29.8	13	61	49	55.6	49.1
AC		24	21.3	17.7	22.6		11	10.9	12.8	12.3		5	−13	−8.6	−12
S-AC		−30	−32	−24	−28		−29	−25	−27	−31.9		−36	−31	−34	−35
AcetAV		28	28.2	27.8	28.1		26	27.8	27.9	28.1		23	21.5	22.6	22.8
CE	2	20	16.9	20.4	17.6	2	41	34	41.3	39.8	14	44	37.2	47.3	36.9
AC		23	24.2	20.9	24.8		8	5.4	6.1	3.4		2	4.2	0	0.5
S-AC		−28	−25	−28	−30		−29	−31	−32	−36.6		−32	−31	−25	−28
AcetAV		21	17.3	13.7	16.8		–	14.4	17.7	13.7		24	22.5	25.5	21.7
CE	3	18	13.7	14.7	15.1	3	28	26.6	26	28.5	15	34	33.4	46.2	37.1
AC		15	22.3	22	21.9		14	10.9	6.8	11.2		−4	−6.6	−7.7	−6.5
S-AC		−34	−35	−33	−36		−32	−34	−28	−33.7		−34	−33	−40	−32
AcetAV		20	27.8	24.2	26.2		28	29.8	27.8	29.4		20	19.7	23.6	19.6
CE	4	14	7.5	10.6	7.5	4	36	26.7	29.6	31.9	16	45	41.3	49.4	39.8
AC		26	34.3	24.9	30.7		3	5.9	0	9		2	1.1	9	3.1
S-AC		−31	−37	−23	−34		−29	−35	−32	−29.4		−34	−31	−29	−33
AcetAV		13	25.2	26.2	18.2		9	28.6	25.1	11.6		10	8.8	10.4	7.9
CE	5	11	2.4	0	3	5	66	61.1	50.5	60.4	17	40	29.2	30.5	29.1
AC		21	25.6	16.2	21.6		−12	−14	−15	−11.9		−3	0	0	0.8
S-AC		−32	−26	−26	−37		−28	−32	−23	−34.2		−35	−31	−31	−31
AcetAV		15	18.2	18.2	18.9		13	17.7	15.9	17.7		26	28.2	28.2	28.1
CE	6	12	11	14.7	10.9	6	42	35.6	42.2	36.8	18	45	42.4	49.4	42.2
AC		23	27.2	26.6	27		−4	0.9	−5.7	−2.1		−1	−9.4	−11	−12
S-AC		2	−15	−7.4	−21		−38	−42	−39	−43.2		−31	−34	−33	−36
AcetAV		27	26.6	24.6	26.1		−2	2.8	5.6	−0.8		12	9.9	13.2	11.6
CE	7	3	3.4	7	3.5	7	33	26.9	32	29.8	19	31	26.6	30.3	28.5
AC		20	24.9	24.1	21.4		0	3.2	0	2.5		8	15.8	12.7	13.6
S-AC		−20	−3.2	−9.8	−9.5		−40	−38	−40	−40.8		−28	−33	−29	−33
AcetAV		10	16.8	16.2	15.7		0	1	3.8	−3.8		13	16	13.5	15.7
CE	8	−1	−6.1	−5.7	−9	8	51	35.3	50.9	41.3	20	36	35.3	35	36.7
AC		27	45.3	41	44.8		9	3.7	3.9	3.2		−3	3.5	6.5	1.2
S-AC		−4	−2.2	−13	–		−16	−10	−14	−25.6		−36	−34	−35	−34
AcetAV		29	27.2	26.2	26.1		42	35.5	39.4	39.1		18	14.5	12	15.7
CE	9	31	19.2	25.4	24	9	51	44.7	46.7	47.9	21	58	46.3	56	46.4
AC		8	5.5	6.8	8.2		−13	−12	−10	−10.6		−1	1	0	−1.9
S-AC		−31	−27	−27	−32		−27	−32	−29	−34.9		−33	−32	−39	−34
AcetAV		17	15.8	16.8	15.2		29	26.1	25.6	24.7		14	13.8	16.3	13.7
CE	10	15	13.1	18.4	18.4	10	42	38.5	38.1	39.4	22	46	37	40.2	36.9
AC		22	20.9	10.3	17.9		3	4.5	5.6	5.6		3	3.7	0	2.6
S-AC		−27	−21	−14	−27		−33	−27	−27	−36.7		−35	−34	−33	−35
AcetAV		21	19.8	19.9	17.5		25	15.3	15.9	14.4		28	25.5	24.4	24.4
CE	11	22	19	20.4	21.8	11	46	39.2	42.4	44.1	23	41	37.8	38.4	39.1
AC		18	24.3	20.9	22		1	0.1	0	−0.6		0	0.5	0	−1.3
S-AC		−22	−21	−16	−29		−28	−28	−22	−34		−31	−30	−26	−32
AcetAV		31	28.3	27.6	29		37	35.7	34.4	36.5		20	17.3	15.7	16.5
CE	12	13	6.9	9.2	9.6	12	41	30.9	39	33	24	41	32.5	37.4	32.5
AC		24	38.9	27.1	32.8		2	5.8	12.6	6.7		11	13.1	13.8	12.1
S-AC		−6	−1.4	−6.1	−8.8		−29	−24	−23	−27.6		−33	−35	−33	−34
AcetAV		32	37.1	37.8	39		27	33.8	34.7	32		15	26.4	23.2	–

Using the control data set, the mean difference (± standard deviation) between each observer and the control data was found: 0.04 ± 3.52° for Observer 1 (O1); −0.46 ± 3.13° for Observer 2 (O2); and 0.42 ± 2.71° for Observer 3 (O3). The mean difference (± standard deviation) of the computerized method was −1.30 ± 3.30°.

The maximum difference between any two manual observers was 19.6° and was observed between O1 and O2 when measuring the postoperative AcetAV of Patient 4. A comparison between the computerized technique and the average manual observations shows a maximum discRepancy of 11.9°. Figure 4. shows a histogram of the errors of each observation with respect to the control data, and demonstrates a normal Gaussian distribution.

Figure 4. Histograms of measuring error for observers 1–3 (O1-O3) and the computer assisted Lunate-Trace method (LT).

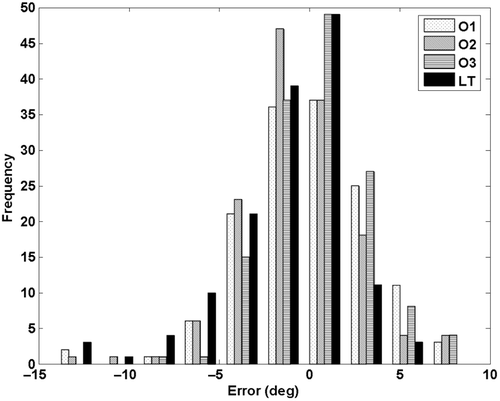
A one-way ANOVA including all the measured angles indicated a significant difference (p < 0.001) between the observation groups. The post-hoc multiple comparison of the ANOVA results identified the mean error for the computer technique as being significantly different from that for two of the three manual observers (O1 and O3).

Factors analysis

Each data set was also analyzed to identify a possible discrepancy associated with a particular angle type (CE, AC, S-AC, AcetAV). Two of the manual observers (O1, O2) had significantly more error (p < 0.001) associated with the CE angle than with the other measurements. Grouping the data by angle type also demonstrated that, for the computerized measurement technique, significantly different mean error was associated more with the S-AC angle on the sagittal plane than with any other (p < 0.001). The inter-observer errors for the CE, AC, S-AC, and AcetAV are presented in Table II..

Table II.  Error distributions (mean ± standard deviation) for each observer based on the type of angle measured. Two manual observers showed significant (p < 0.01) discrepancies in measuring CE angles. The computerized Lunate-Trace method (LT) showed significant error associated with the S-AC angle measured on the sagittal plane.

Angle	O1	O2	O3	LT
CE	2.2 ± 3.0*	−3.1 ± 2.5*	1.0 ± 3.0	−1.3 ± 2.7
AC	−0.3 ± 3.6	1.0 ± 3.1	−0.7 ± 2.5	0.2 ± 2.5
S-AC	−0.9 ± 3.0	−0.15 ± 3.1	1.1 ± 2.8	−3.4 ± 4.1*
AcetAV	−0.8 ± 3.5	0.45 ± 2.2	0.4 ± 1.9	−0.8 ± 2.5

Based on the patient type (dysplastic preoperative, dysplastic postoperative, and normal), an analysis of variance indicated that the mean error did not differ significantly on the basis of joint pathology using the Lunate-Trace method (p = 0.58). The analysis shows that the computer algorithm is valid for hips classified as normal or dysplastic.

Acetabular versus femoral center

Under dysplastic conditions, the acetabular and femoral centers may not coincide. We found that the average difference between the acetabular center of curvature and the femoral head center was 4.18 ± 2.06 mm for the dysplastic preoperative group, as compared to 1.69 ± 0.87 mm for the normal group. This difference was significant (p < 0.001). The predominant direction of the femoral head center with respect to the center of rotation of the acetabulum for the dysplastic cases was superior (3.2 ± 2.3 mm), medial (0.9 ± 1.7 mm), and anterior (0.6 ± 1.1 mm) (see Figure 5.). The center of the femoral head for the normal patients was found, on average, to be directed 0.7 ± 1.1 mm medial, 0.2 ± 0.6 mm anterior, and 0.7 ± 1.1 mm inferior to the acetabular center of curvature.

Figure 5. Vector plots of location of femoral head with respect to acetabular joint center (mm) in the superior-lateral (frontal plane) and superior-anterior (sagittal plane) directions. [Color version available online.]

Discussion

In this study, we developed a custom algorithm (Lunate-Trace), designed for intraoperative use, for measuring radiological angles based on a segmented model of the hip joint, and evaluated its performance in comparison to expert manual observation. The mean and standard deviation of error for the computerized Lunate-Trace method was comparable to the errors of the manual observers. The mean difference between the computerized measurements and the control data set was 1.3°. While this mean error was significantly different from that for two of the three manual observers, we consider it to be reasonable in terms of the PAO procedure, which involves rotations of the fragment in the coronal plane that averaged 27° for our 12 cases (range 11–55°). The standard deviation of errors for the computer method (3.31°) was comparable to the standard deviations within the manual observer group (range: 2.71–3.52°).

Statistical analysis showed that the S-AC angle in the sagittal plane was the major contributor to error in the computerized method. The computer measures the S-AC angle from the superior roof of the acetabulum, which is based on an interpolation of the medial and lateral edges. This is a likely source of the error, because the measurement is not based on true CT image data. Future revisions to the algorithm will investigate methods for more accurately determining the acetabular roof and hence the S-AC angle.

For the manual observers, the maximum error (19.6°) occurred when measuring the AcetAV angle in the transverse plane for the postoperative outcome of Patient 4. Because of the PAO reorientation, the anterior portion of the fragment was situated such that a drastic change in anteversion occurred over only a few sequential transverse slices. Since the center of the femoral head was selected manually and predicates the transverse slice used for measuring, considerable differences can result if observers estimate differently in the superior-inferior direction [21].

Other sources of inter-observer error lie in the use of anatomically based landmarks from CT data. For the four angles measured manually in this study, error originates with the accuracy/consistency with which the observer selects the femoral head center and the acetabular landmark. The error associated with picking a landmark on CT image data of finite resolution is found in radians (assuming small angles) as the quotient of the resolution and the measuring distance. A landmark selected with an accuracy of ±1 voxel with a resolution of ∼1 mm over a distance of 28 mm (femoral head radius) results in ± 2° error. Selection of the femoral head is critically important for CT-based measurements because it defines the sagittal, coronal and transverse slices presented to an observer to permit measurement of the anatomical angles. This limitation is unique to CT reformats, since only a single image slice of finite resolution is used for measuring angles.

Janzen et al. [16], [17] described a method in which oblique CT reformat slices were acquired at the level of the femoral head center and rotated about a superior-inferior axis in 10° increments from anterior (0°) to lateral (90°) to posterior (180°). The center-edge angles (CEAs) were measured on each slice to characterize normal and dysplastic joint coverage. Their study did not define the entire joint margin, including the medial and lateral aspects. By connecting the points around the acetabulum to form a closed and continuously defined 3D spline curve, as in our study, the radiographic angles can be measured continuously at any orientation, not just at discrete locations. In the study of Janzen et al., inter-observer error using oblique CT slices ranged from 1.7° to 7.9° [16] between two observers, with greater error along the posterior acetabular rim. In our study, the maximum discrepancy between three manual observers was higher.

The main limitation of this computerized technique is its reliance on manual input during the segmentation aspect of the computational procedure. The observer makes selections on 2D images acquired circumferentially about the hip joint. Inputting more data points requires more time than with the traditional radiological techniques; however, we designed the application to minimize user input and reduce segmentation time. The entire process takes less than 5 minutes to finish and allows a more complete characterization of the anatomy. Once segmented, the angle calculations are instantaneous as the contact surface is reoriented. A second limitation is that the radiological metrics evaluated (CE, AC, S-AC, AcetAV) rely on the selection of the femoral head center, which determined the CT slices in the coronal, sagittal, and transverse planes. Evaluation of these angles on patients with non-spherical femoral heads may introduce additional errors. Finally, the segmentation method relies on the continuous nature of the lunate surface of the acetabulum. If the joint space is compromised during the PAO, this invalidates the continuity assumption and will result in errors in reporting the angles because the actual lunate surface no longer corresponds to the preoperatively segmented surface.

The use of radiographs versus CT data for describing the 3D nature of the hip joint has been debated[9], [10], [27]. Previously, some authors used AP radiographs to describe the acetabular contact surface by mathematical interpolation based on the femoral head center and radius [10], [24–26], [28]. Because our algorithm allows characterization of the acetabulum independent of the femur, a parameter comparing the center of the acetabulum and the femoral head center point is possible. In this study, we showed that the separation distance between the femoral head center and the center of curvature of the acetabular cup was significantly greater (p < 0.001) for dysplastic hips preoperatively (mean: 4.2 mm) than for normal hips (mean: 1.7 mm). The results justify the use of CT data rather than radiographs for characterizing the geometry of dysplastic hips when the curvature centers may not be coincident. The dissociation of acetabular and femoral centers is consistent with the onset of joint subluxation and abnormal joint morphology associated with DDH. Evaluating the acetabulum independently of the femur offers a potential method for assessing subluxation and its correction during surgery.

Successful intraoperative navigation of some surgical instruments during PAO has been reported [15], [19–31]. Tracking of the acetabular fragment has also been described, but the fragment orientation was reported only as macroscopic rotations about the anatomical planes. Because the bony anatomy is a 3D non-uniform structure, attempting to apply rotations to the acetabular fragment about multiple axes will result in uncorrelated changes in the anatomically based angles. In order to better plan and execute the PAO procedure, an accurate and complete computer model of the contact surface of the joint is important. The Lunate-Trace computerized method, described in this paper, completely defines the load-bearing lunate surface of the acetabulum, and thus has the potential to extend the application of intraoperative navigation to include optimization of fragment alignment and continuous feedback regarding radiological angles.

To conclude, the comparison between this algorithmic method and careful manual measurement yields comparable accuracy. The advantage offered by the computational Lunate-Trace technique is the automatic angle calculation and recalculation during reorientation of the acetabulum, with potential applications in preoperative planning and image-guided surgery.

Acknowledgments

This work is supported by grant number R21 EB002881-01 from the National Institute of Biomedical Imaging and Bioengineering (NIH/NIBIB).