HMM assessment of quality of movement trajectory in laparoscopic surgery

Abstract

Laparoscopic surgery poses many different constraints for the operating surgeon, resulting in a slow uptake of advanced laparoscopic procedures. Traditional approaches to the assessment of surgical performance rely on prior classification of a cohort of surgeons’ technical skills for validation, which may introduce subjective bias to the outcome. In this study, Hidden Markov Models (HMMs) are used to learn surgical maneuvers from 11 subjects with mixed abilities. By using the leave-one-out method, the HMMs are trained without prior clustering of subjects into different skill levels, and the output likelihood indicates the similarity of a particular subject's motion trajectories to those of the group. The results show that after a short period of training, the novices become more similar to the group when compared to the initial pre-training assessment. The study demonstrates the strength of the proposed method in ranking the quality of trajectories of the subjects, highlighting its value in minimizing the subjective bias in skills assessment for minimally invasive surgery.

• Laparoscopic surgery
• training
• Hidden Markov Model
• skills assessment

Introduction

Minimally Invasive Surgery (MIS) was first introduced over 20 years ago [1], [2]; however, many surgeons are still restricted to performing relatively simple procedures, for example, laparoscopic cholecystectomy and diagnostic arthroscopy. The uptake of advanced MIS procedures, such as laparoscopic colectomy for cancer [3] and therapeutic arthroscopy, is still very slow in many countries. These procedures are mainly reserved for tertiary referral centers and are performed by highly sub-specialized surgeons.

The constraints imposed by the MIS environment have been well documented; the lack of 3D vision [4], limited haptic feedback [5], and the fulcrum effect [6] restrict the variety of surgery performed. It is quite clear, however, that some surgeons are superior to others in performing these tasks [7]. This has motivated extensive research into the objective assessment of surgical skills [8]. The methodology has now evolved from subjective qualitative assessment by the trainers and knowledge assessment using post-graduate examinations [9] to objective quantitative approaches using time or movement parameters [10]. Quantitative methods for assessing surgical dexterity have been widely validated for a number of open and laparoscopic procedures [11]. The validation of these methods, however, relies upon prior definition of expertise, and this classification is mostly based on the assumption that experience equals technical excellence.

Rosen et al. applied Hidden Markov Models (HMMs) using a series of 14 finite states defined by the surgeons’ instrument-tissue interactions [12]. These states were based on the force and torque (F/T) signatures collected by using two sensors to measure the forces and torques applied at the interface between the surgeon's hand and the instrument. The HMMs classified the actions into specific maneuvers and the transitions between them. The skill level of each surgeon was then calculated by the statistical distance of their HMMs from those of the expert surgeons. The method, however, relied on a previous definition of expertise, and the scoring system was based on the individual difference from this definition. To obtain the F/T signatures, each video frame was also visually analyzed by two experts.

The purpose of this study is to examine the use of HMMs based on view-invariant trajectory representations for assessing MIS tasks. To increase the complexity of hand-eye coordination, view rotation tasks have been introduced. The effect of such complications has been studied previously [6], [13], [14], with the results indicating a detrimental effect on the performance of surgeons and novices. Furthermore, it has been suggested that the ability to handle mental rotation tasks is indicative of innate ability in mastering laparoscopy [15]. We demonstrate that, with the proposed method, a probabilistic framework can be formulated to allow the observation of trajectories without prior, arbitrary classification of the subjects’ abilities, thus minimizing subjective bias in MIS skills assessment.

Methods

Instrument tip tracking and calibration

To obtain the trajectory of the instrument tips in Euclidean space without interfering with the experimental task, a tracking device was attached rigidly to the handles of the laparoscopic instruments. For accurate positioning of the tracking device, a Polaris infrared (IR) tracker (Northern Digital, Inc., Waterloo, Ontario) with 6 degrees of freedom (DOF) was used. The Polaris is able to track a number of passive, active, wired and wireless IR tools in real time simultaneously. Data interfacing was achieved through RS-232 and the provided tracking accuracy is 0.35 mm RMS at a sampling rate of 60 Hz. The offset of the instrument tips from the IR markers was calculated using the Pivot function in the NDI ToolViewer Software version 3.02.01.

The accuracy of the instrument tip tracking arrangement was further assessed by mounting the laparoscopic instrument on a Stäubli RX60L robotic arm with repeatability accuracy of ±0.02 mm and 6 DOF. Ten points for calibration were set up using the robotic arm to manipulate the instrument whilst the IR markers were being tracked.

Subjects and experimental setup

Eleven subjects were recruited for the study (9 medical students and 2 practicing surgeons; 2 subjects were left-handed). None of the medical students had previous experience with simulated or real laparoscopy. The subjects were randomized into two groups. All subjects were consented prior to the study, and were given a short introduction to laparoscopic surgery and the instruments used. Both groups were required to perform a laparoscopic task in a box trainer, after familiarization with the instruments and environment. A Karl Storz laparoscopic stack with an S1 camera head, Xenon Nova light source, and Hopkins II 0° endoscope was used for the experiment, along with two laparoscopic graspers with IR tracking devices rigidly attached.

For both groups, the first task was to locate two standardized points (A and B) on a simulated plastic small bowel model, as illustrated in Figure 1, using laparoscopic graspers. Each point was attached to an in-house-designed touch-sensitive circuit switch to mark the beginning and end of each trajectory. Each time the circuit was completed, an alarm indicated a successful contact. The subjects were then asked to touch alternately the points A and B 10 times with the left instrument, and then with the right instrument, and this step was repeated. A total of 36 trajectories were obtained between the two points. For the second task, subjects were required to repeat the first task with the laparoscopic camera rotated 90° counter-clockwise for Group 1 subjects and 90° clockwise for Group 2 subjects.

Figure 1. Experiment setup showing the arrangement of the IR sensors in relation to the laparoscope tools (a), and the plastic small bowel model with a simulated omental flap with and without the camera view being rotated (b, c). [Color version available online.]

Five subjects (3 from Group 1 and 2 from Group 2) underwent further training in which three sessions were completed with the laparoscopic camera rotated 90° counter-clockwise and three sessions with the camera rotated clockwise, followed by a final post-training assessment using normal camera orientation.

For the analysis of the trajectories, the experiments were divided into (1) left instrument motion from point A to B; (2) left instrument motion from point B to A; (3) right instrument motion from point A to B; and (4) right instrument motion from point B to A.

View-invariant representation of 3D trajectories

Prior to HMM analysis, the 3D trajectories were mapped to a view-invariant representation based on the Centroid Distance Function (CDF) [16]. The instrument tip positions from IR tracking after offset correction were modeled as a parametric curve:

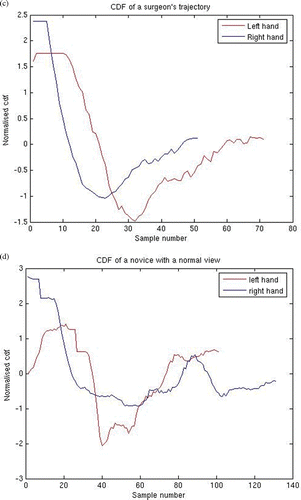
CDF is a feature that is affine-invariant, and is also widely used in image retrieval applications [16]. The centroid is defined as the weighted average of all the points of each particular trajectory, and, in essence, CDF describes a time series of the Cartesian distance of each point in the trajectory from the centroid. Scale normalization transforms the CDF values into standard normal distributions which are rotational and translational invariant. Other affine-invariant representations based on local angle and velocity measurements [17] were considered; however, these methods were sensitive to local variations in the trajectories and were not used for this study. A previous study compared CDF with curvature scale space, and showed that CDF with HMMs yielded better recognition of trajectories [16]. Both methods, however, offered rotation-invariant representations of trajectories. CDF significantly simplifies the subsequent HMM classification by foregoing cumbersome pre-processing steps. Figures 2a and 2b show the CDF projections of instrument trajectories for a surgeon and a novice, respectively.

Figure 2. (a, b): 3D trajectories of surgeon and novice; blue represents the right hand and red the left. (c, d) (on next page): CDF representation of the same trajectories. [Color version available online.]

Hidden Markov Modeling

Hidden Markov Models are finite-state stochastic machines that allow dynamic time warping for modeling time series data. HMMs have been used to classify movement trajectories, though segmentation was necessary to avoid violating the Markovian property which assumes independence of a current state from past states given the previous one [18]. Each trajectory was regarded as one independent action, and the CDF for the trajectory was used as input signal to the HMM, hence the notion that each trajectory adhere to the Markovian assumption. In this study, HMMs were used to learn each trajectory of a given experiment and view rotation. The leave-one-out method was used to train the HMM from all subjects excluding the test subject's data. The trained HMM was then used to calculate the log likelihood of the test subject and indicate similarities to or differences from the learned model.

An HMM can be described by three model parameters representing the relationship between the hidden states (h) and the observed data (x). These parameters are:where π_i is the initial state probability, a_ij the transition matrix between the hidden states, and p(x|h) the probability of generating an observation given the hidden state. In this study, a fixed number of states were used. However, in order to have a more flexible model, the observation probabilities were modeled by a Gaussian Mixture Model (GMM). Thus p(x|h) can be defined as:where c_m is the mixing parameter, and μ_m and Σ_m are the mean and covariance matrix of the component m of the GMM.

The K-means algorithm was used to initialize the parameters of the observation GMM (mainly the means μ_m). Two versions of the K-means algorithm were implemented to compare performance, using Euclidean distance and Derivative Dynamic Time Warping [19] to calculate the similarity between two trajectories. The second option can take signal “warping” into consideration when finding cluster centers, and the length of the “warping” was then used to normalize the distance between the two trajectories. As the resulting cluster centers were identical with both methods, Euclidean distance was used as it was more computationally efficient. The Expectation Maximization (EM) algorithm was used to calculate the maximum likelihood of the parameters of the HMM, namely the means and covariances of the components of the GMM and the parameters π_i and a_ij.

The parameters of the HMM, including the number of Gaussians in the observation GMM, as well as the number of hidden states of the HMM, were selected experimentally. Parameters that led to the least variation in the values of the test data likelihoods were selected as the parameters that could provide good data representation for this dataset. The number of hidden nodes was selected as 4 with a mixture of 2 Gaussians for the GMM.

Categorized observational score

The videos of all the tasks were scored by two independent observers who were blinded to the identity of the subjects. The scoring system used was a modified version of the Objective Structured Assessment of Technical Skills (OSATS) global rating scale. This is a widely validated score developed by Martin et al. [20], using 8 categories each with a Likert scale of 1–5 anchored by descriptors. The modification was necessary as 3 of the categories (suture handling, knowledge of procedure, and quality of final product) did not apply to this particular experiment (see Table I). Inter-observer reliability was calculated using Cronbach's alpha test.

Table I.  Modified version of the Objective Structured Assessment of Technical Skills (OSATS) global rating scale.

GLOBAL RATING EVALUATION OF PERFORMANCE
Please circle the number corresponding to the candidate's performance regardless of their level of training
Respect for tissue
1	2	3	4	5
Frequently used unnecessary force on tissue or caused damage by inappropriate use of instruments.		Careful handling of tissue but occasionally caused inadvertent damage.		Consistently handled tissues appropriately with minimal damage.
Time and Motion
1	2	3	4	5
Made unnecessary moves.		Efficient time/motion but some unnecessary moves.		Clear economy of movement and maximum efficiency.
Instrument
1	2	3	4	5
Frequently asked for wrong instrument or used an inappropriate instrument.		Competent use of instruments although occasionally appeared stiff or awkward.		Fluid moves with instruments and no awkwardness.
Flow of operation
1	2	3	4	5
Frequently stopped operating or needed to discuss next move.		Demonstrated some forward planning and reasonable progression of procedure.		Obviously planned course of operation with efficiency from one move to another.
Overall
1	2	3	4	5
Very poor		Competent		Clearly superior

Results

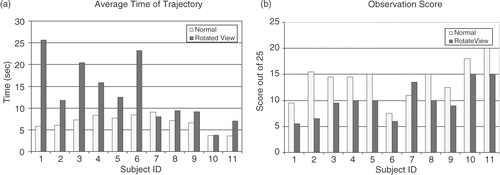
To demonstrate the extent by which view rotation increases the complexity of the tasks, Figure 3a illustrates how the average time for a subject to complete a trajectory increases when the view is rotated. Figure 3b demonstrates how the OSATS global rating scale (with strong inter-observer agreement, α = 0.914) decreases with view rotation; however, this does not completely correlate with the time measurement (r = −0.818, p = 0.002). For example, Subject 2 in the rotated task had the third lowest score in OSATS, but had the fifth longest time. There is a significant correlation between mean (unfiltered) path length and time taken (r = 0.916, p < 0.001) and, in the rotated task, between path length and OSATS score (r = −0.873, p < 0.001). Interestingly, one subject improved slightly in the rotated task (Subject 7).

Figure 3. (a) Average time for the trajectories of each subject. (b) Modified OSATS score for all subjects involved in the experiments.

CDF representations of motion trajectories are illustrated in Figure 4a. This figure shows that, in this particular experiment, the surgeon's trajectory generally lies closer to the mean of all the CDFs than that of the novice. However, the average CDF trajectory is distinctly different in shape from either of the sample trajectories.

Figure 4. (a) Mean CDF trajectory for one of the experiments with standard deviation. Examples of a practicing surgeon's trajectory (in black) and a novice's trajectory (in pink) are shown. (b) The HMM learned curve is shown in green. [Color version available online.]

In Figure 4b, the HMM learnt curve is plotted. This is the average of ten observations after training the HMM. Examples of surgeon and novice trajectories are plotted for comparison, showing that the surgeon's trajectory is more similar in shape to the HMM learnt curve. However, the set of trajectories showed a large variability with effects of time warping. By calculating the likelihood to the HMM, a measure of similarity of a certain trajectory to the whole group can be obtained.

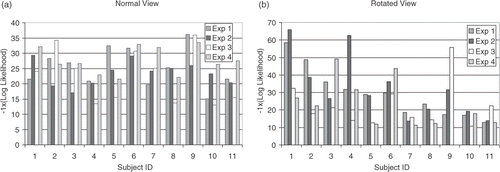
The log likelihoods of the subjects’ trajectories belonging to the training data sets by using the leave-one-out method are shown in Figure 5a and b. Lower values indicate that the subjects’ trajectories are more likely to match the models learnt by the HMMs. The log likelihood values are negative. The effect of view rotation accentuates the difference between the subjects, as shown in Figure 5b.

Figure 5. Negative log likelihood of the subject in each experiment belonging to the group (a) in the normal view orientation and (b) in the rotated orientation.

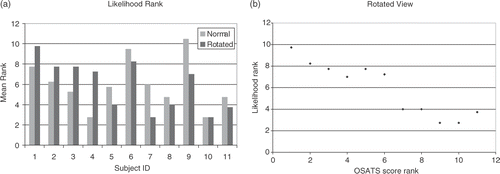
In this study, the log likelihood values are ranked in each experiment independently, rank number 1 representing the most similar. The mean rank of experiments 1–4 for each subject is calculated for both normal and rotated view in Figure 6a. In order to compare this with the most validated surgical rating scale, this ranking is plotted against the ranking in the OSATS score in Figure 6b. There is a very significant correlation between the rankings (r = 0.93, p < 0.001).

Figure 6. (a) Mean rank of subjects’ likelihood of belonging to the test group. (b) Scatter plot of the rank of likelihood generated by the trained HMM against OSATS score ranking in the rotated tasks.

Pre- versus post-training

Figure 7 shows the CDF representations of the post-training motion trajectories. This series of figures shows that the means of the post-training trajectories generally lie closer to the means of all the CDFs. This appears to be more pronounced in Trajectories 3 and 4, which are the movements of the right hand.

Figure 7. Means of CDF for all four trajectories with standard deviation. Means of the pre- and post-training data are plotted in black and pink, respectively. [Color version available online.]

The log likelihoods in Figure 8 were calculated using the leave-one-out method as described above; however, only the five novices’ pre- and post-training and the two surgeons’ trajectories were used as the training data sets. Figure 8a shows that, in all 4 experiments, the log likelihood is lower (i.e., more similar to the training data sets) in the post-training sessions; however, this is not statistically significant. Figure 8b illustrates the likelihood rank of individual subjects’ trajectories before and after training.

Figure 8. (a) Box plot of the negative log likelihood of subjects’ pre- and post-training data belonging to the test group where the median (line), inter-quartile range (shaded box), range of the data (whiskers), outliers (circles) and extremes (stars) are plotted. [Color version available online.] (b) Likelihood ranks of individual subjects’ trajectories before and after training.

Discussion

This study has shown that Hidden Markov Modeling can be used to learn models of surgical motion trajectories, even in a group of subjects with mixed abilities, without prior classification of technical skill levels. The proposed models learn all the trajectories between two targets from the subjects, and then rank the subjects in terms of consistencies to the trajectories. As the subjects’ skill levels improve, their movements between the two targets become more consistent, and hence lead to a lower likelihood output. This seems to be particularly effective when the tasks are performed in difficult laparoscopic environments, e.g., with camera rotation, where the difference in skills performance is more pronounced. Furthermore, this technique is shown to be sufficiently sensitive to distinguish the effect of the short duration of skills training on the subjects.

Although objective quality scoring systems such as OSATS have been validated and shown to be reliable, these methods are labor intensive and require invaluable time from surgical experts. The speed of a surgeon has long been used as a benchmark for skills; however, time is considered a crude metric for performance, whereas OSATS concentrates on the quality of technique. Even in this study, discrepancies are apparent between the ranking of OSATS and time performance. Dexterity analysis has been developed to provide a more efficient approach to surgical skills assessment; again, parameters such as path length and number of movements may have neglected the importance of the quality aspect in skills evaluation. Nevertheless, it remains an effective tool for assessing the performance of simple and highly standardized procedures.

In this study, HMMs calculated the likelihood of similarity between each individual subject and the learnt trajectories of the group, using the leave-one-out method. This likelihood correlated very well with the observation scores, and perhaps this can provide an automated quality scoring system. The second advantage of HMMs is the ability to learn models of surgical motion trajectories in a group of subjects with mixed abilities, and the approach successfully calculated the likelihood of the practicing surgeons as being amongst the most representative trajectories (subjects 10 and 11 in Figure 6a). Subject 7 had a lower likelihood rank than Subject 11 (a surgeon), and this was reflected in Figure 6b, where the OSATS score was ranked at 9. This was due to the following factors: First, there may have been a “ceiling” effect where the subject's performance was limited by the methodology used and the scoring system was inadequate to discriminate the performance further due to the simplicity of the task [21]. Second, Subject 7 had unusual spatial awareness, most likely due to her previous training as an airplane pilot.

A potential criticism of the study would be the small study population, and the biased proportion of novices as compared to surgeons. It should be noted, however, that even with 11 subjects a significant correlation could be found between the HMM-calculated likelihood and OSATS, which is considered to be the “gold standard” in skills assessment. This further illustrates the sensitivity of the current method. Furthermore, the inclusion of the data for the two surgeons enabled a demonstration of its ability to differentiate subjects both within the same skills group and in different skills groups.

One of the important considerations in applying the proposed HMM scheme is the feature representation of the trajectories. In general, it should be invariant to affine transformation, as this can cope with trajectories with different starting points, rotations, and approach directions. In this study, we have used CDF as a means of invariant feature representation. Other approaches based on extremes in acceleration measured by high-frequency wavelet coefficients are also applicable [22]. This technique should be explored in complex laparoscopic procedures and validated in a larger-scale study.