New approaches to online estimation of electromagnetic tracking errors for laparoscopic ultrasonography

Abstract

In abdominal surgery, a laparoscopic ultrasound transducer is commonly used to detect lesions such as metastases. The determination and visualization of the position and orientation of its flexible tip in relation to the patient or other surgical instruments can be a great support for surgeons using the transducer intraoperatively. This difficult subject has recently received attention from the scientific community. Electromagnetic tracking systems can be applied to track the flexible tip; however, current limitations of electromagnetic tracking include its accuracy and sensibility, i.e., the magnetic field can be distorted by ferromagnetic material. This paper presents two novel methods for estimation of electromagnetic tracking error. Based on optical tracking of the laparoscope, as well as on magneto-optic and visual tracking of the transducer, these methods automatically detect in 85% of all cases whether tracking is erroneous or not, and reduce tracking errors by up to 2.5 mm.

• Electromagnetic tracking
• optical tracking
• hybrid tracking
• image-guided surgery
• augmented reality
• laparoscopic surgery

Introduction

Laparoscopic ultrasonography (LUS) nowadays plays an increasing role in abdominal surgery. Its main application areas include the examination of the liver, biliary tract, and pancreas. Unfortunately, LUS is often difficult to perform, especially for novice surgeons. Therefore, several groups have tried to support surgeons by providing navigated LUS, in which the position and orientation (“pose”) of the ultrasound transducer is estimated using robot or optical tracking (OT) [1], electromagnetic tracking (EMT) [2–5], or magneto-optic tracking, i.e., a combination of OT and EMT [6].

Optical tracking, known to be one of the most accurate tracking technologies, always requires an unobstructed line of sight to OT bodies. This cannot be established using flexible instruments in minimally invasive surgery. Mechanical tracking, i.e., the use of robotic control and thus additional hardware, is only justified in the presence of a robotic guidance system such as the da Vinci telemanipulator. The only currently available method for tracking flexible instruments is EMT.

When using EMT clinically, fast sensor movements and distortion of the EMT field are significant problems which lead to erroneous tracking data. Electrically powered or metallic objects within or close to the working volume can cause this distortion. For example, operating room equipment such as surgical tools, instruments, the operating table, or imaging devices such as a C-arm and CT scanner can lead to tracking errors of several millimeters or centimeters [7], [8]. Many calibration techniques have been presented to correct measurement errors caused by the presence of stationary ferromagnetic objects [9]. To use such a calibration technique, the user or a robot has to record many well-distributed distorted measurements inside the EMT volume, along with their corresponding undistorted values. These measurements are used for a field distortion function based on polynomials or look-up tables, which reduces the static errors caused by a specific stationary operating room setup. This time-consuming and laborious calibration process needs to be repeated for every new intervention, as the operating room setup, and hence the distortion field, changes between interventions. Additionally, instrument movements or the relocation of the EMT transmitter can cause dynamic changes in the field distortion, and a previously computed distortion correction function will not be able to deal with such dynamic changes. Therefore, researchers began to develop solutions for detecting dynamic changes in the field distortion [10], [11]. Their common idea is to integrate two (rigidly connected) EMT sensors into a pointer or instrument in order to obtain redundant measurements. If these measurements do not reflect the fixed distance between the two sensors, tracking errors can be identified and a plausibility value generated.

This paper builds upon our previous work [12–14] and describes two new approaches to detecting and partially correcting EMT errors online, i.e., intraoperatively, without a pre-computed distortion correction function. Both methods are applied to a flexible laparoscopic transducer, the pose of which is determined by a magneto-optic tracking system. A rigorous accuracy evaluation of both online EMT error estimation methods was conducted. As an exemplary application of the improvement in the tracking quality, the B-scan images of the transducer are overlaid on the live images of an optically tracked laparoscope in real time. This may provide surgeons with a better understanding of the spatial relationship between the two imaging modalities and guide them with the required accuracy and reliability.

System setup

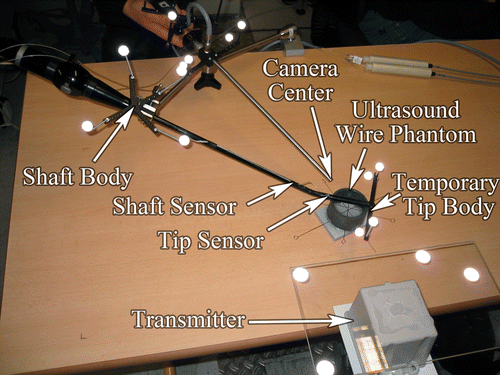
Our hardware setup consists of the following components: A SONOLINE Omnia ultrasound system (Siemens Medical Solutions) equipped with a flexible laparoscopic linear array transducer (LAP8-4, 5 MHz, 10 mm diameter); a laparoscopic camera with a forward-oblique 30° HOPKINS telescope (Storz); a workstation PC including two frame grabbers (for capturing the transducer and camera video in real time); and our hybrid magneto-optic tracking system. Its optical component comprises 4 ARTtrack2 cameras and a book-size PC running the DTrack tracking software. The electromagnetic component is a 3D Guidance unit (Ascension Technology Corporation, Burlington, VT) equipped with a mid-range transmitter and insulated 1.3-mm sensors, which have a total diameter of 1.7 mm including the vinyl tubing. Time synchronization of all (video and tracking) data streams, visualization, and the user interface is implemented within our medical augmented reality software platform CAMPAR [15].

Methods

In the following section, the term “body” always refers to an optical tracking (OT) body usually consisting of four or more retroreflective spheres, while “sensor” always refers to a wired electromagnetic tracking (EMT) sensor. Both types are used to acquire 6-DOF pose information in their respective tracking coordinate frames.

In addition to an OT body, which is attached to the transducer handle (referred to below as the “shaft body”), two EMT sensors are attached to the transducer: one to the flexible tip (“tip sensor”) and the other to the rigid shaft (“shaft sensor”), as close to each other as possible. Another OT body is mounted on the EMT transmitter (“transmitter body”). This setup allows us to co-calibrate EMT and OT and to obtain redundant tracking information for the rigid part of the transducer shaft, which is important for detecting EMT errors. Finally, two OT bodies are attached to the laparoscopic camera, one to the head (“laparoscope body”) and the other to the telescope to adjust for telescope rotations.

System calibration

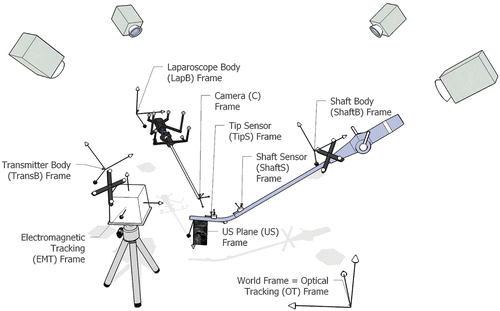
Spatial and temporal system calibration is performed offline in a distortion-free environment. All coordinate frames, which we calibrate to one another, are shown in Figure 1.

Figure 1. Coordinate frames associated with our hybrid magneto-optic tracking setup to localize the laparoscope and the tip of the laparoscopic ultrasound.

Hand-eye calibration

To compute the Euclidean transformation between the shaft body and the shaft sensor frames, the transducer is moved to a set of n stations with distinct rotation axes, so n pairs of poses can be recorded in both the OT and EMT coordinate frames. Two stacked matrices and are then generated from all m = n(n − 1)/2 possible unidirectional motions between these pose pairs. Each stacked matrix therefore consists of m homogeneous transformation matrices. The stacked matrices are related to each other by the equation system , which is commonly written as AX = XB and solved by hand-eye calibration [16].

The same transducer stations can also be used to estimate the rigid hand-eye transformation between the EMT transmitter coordinate frame and its rigidly mounted OT body.

In a final optimization step, the two hand-eye calibration matrices and are optimized for all recorded poses using the Levenberg-Marquardt algorithm. The matrix T_δ ∈ ℝ^4×4 resulting from the transformation chain “shaft sensor to shaft body to OT to transmitter body to EMT to shaft sensor frame”, which ideally would be an identity matrix in an error-free setup, represents the accumulated transformation errors:

From the rotational part R_δ ∈ ℝ^3×3 and the translational part t_δ ∈ ℝ³ of T_δ we can compute a cost function δ that weights translational errors in millimeters to rotational errors in degrees in the ratio 1:3:where the rotational error δ_rotational is the rotation angle of R_δ decomposed into axis-angle parameters.

The 1:3 ratio reflects the root mean squared (RMS) error ratio provided independently by the two tracking system manufacturers: The RMS measurement errors of the OT system are stated as 0.4 mm (position) and 0.12° (orientation), and the static RMS errors of the EMT system as 1.4 mm and 0.5°. (See also http://www.ar-tracking.de and http://www.ascension-tech.com for the specifications of the typical accuracy of both tracking systems.)

We actually optimize both sought transformations and using the results of a closed-form solution [16] as starting values. Although, to our knowledge, no work has been undertaken to evaluate a further optimization, we strongly believe that minimizing the error component relevant to our particular approach improves our performance. The Levenberg-Marquardt algorithm works in real time, as we have a very good initialization. With this initialization, any other iterative optimizer would have given very similar results.

The maximum error δ_thresh of all recorded poses determined after optimization is chosen as a measure of distrust for the overall performance of the hand-eye calibration (see the Online error detection section). Alternatively, an optimal δ_thresh can be selected for specific requirements according to computed receiver operating characteristics (see the Receiver operating characteristics section).

Laparoscopic camera calibration. For camera calibration of the forward-oblique laparoscope, the projection geometry including distortion coefficients [17] and the transformation from laparoscope body coordinates to camera center coordinates are estimated [18]. A more detailed description of this can also be found in our previous work [19].

Transducer tip axis calibration. We calibrate the axis of the transducer tip by rotating a calibration cylinder, which contains an additional EMT sensor at one end, around the transducer tip. Overall, two full 360-degree rotations are performed, the second one with the calibration cylinder flipped. The measurements during the two rotations of the additional sensor describe two circular patterns, which can be used to estimate the transducer tip axis. The axis is stored as a “base point” b_TipS, which is the point on the axis closest to the origin of the tip sensor coordinate frame, and a directional unit vector d_TipS, which points towards the tip, both given in the local coordinate frame of the tip sensor mounted on the flexible transducer tip [13].

Temporal calibration. To provide a smooth visualization without lag, all data is given a time stamp and brought into the same timeframe. While the OT PC and our workstation are synchronized via the Network Time Protocol (NTP) to the same reference time, the ultrasound and EMT systems require a more advanced synchronization. As these systems do not automatically provide reliable time stamps corresponding to the actual data acquisition time, a time stamp is generated when their data arrives at the workstation. Therefore, a fixed offset is subtracted from this time stamp to compensate for any lag introduced while traveling to the workstation. To determine this offset, the magneto-optically tracked transducer is moved up and down and the translation along the principal motion axes is compared, as proposed by Treece et al. [20].

Online error detection

Intraoperatively, for all measurements of the pose of the shaft sensor the deviation from ideal tracking is computed using equation (1). If the corresponding distrust value δ (see equation (2)) is bigger than our previously determined threshold δ_thresh, the surgical staff is automatically warned. Such errors are often caused by dynamic or static field distortions. Additionally, as the tip sensor is in close proximity to the rigid one, its measurements will most likely be affected by these distortions as well, and this can be used for a redundancy-based approach to error correction.

Online error correction

Redundancy-based correction. To also approximate a correction of erroneous measurements of the tip sensor, one approach (also referred to as the tracking redundancy-based approach) is to apply the deviation between the previously hand-eye calibrated (“calib”) and the measured (“meas”) transformation of the shaft sensor to the measured tip sensor transformation, all relative to the fixed OT (world) reference frame:Vision-based correction. Following common surgical procedures, the LUS probe tip already has to be constantly monitored to prevent inadvertent injury to the patient, so laparoscopic images of it are readily available.

As the intrinsic and extrinsic camera parameters of the laparoscope, and hence the spatial location of the image plane, are known, another approach to improving the tracking accuracy of the tip sensor is to automatically detect the transducer tip in the images of the laparoscope camera and align the detected transducer tip axis with the tracked axis.

For an automatic detection of the ultrasound tip, we follow approaches that have already shown promising results under conditions close to real laparoscopic surgery: in a similar manner to Climent and Marés [21] and Voros et al. [22], we use an edge detection filter and a Hough transformation [23] to extract edges from laparoscopic images. We also use additional information to select candidate lines belonging to the transducer edges. Voros et al. [22] and Doignon et al. [24] use information concerning the insertion points of laparoscopic instruments, which stay relatively fixed during an intervention and can thus be used to support the segmentation of instruments. In our case, however, the laparoscopic ultrasound transducer might be bent so that its edges are no longer aligned with the insertion point. Instead of infosssrmation on the insertion point, we use the tracking data of the tip sensor.

1. Line detection. The results of our transducer tip axis segmentation algorithm are illustrated in Figure 2.

Figure 2. Screenshot of axis segmentation. Lines classified as belonging to the transducer tip edges are automatically colored yellow; lines belonging to the transducer (but not to the edges) are colored blue; and the corrected transducer axis is the thick red line. Lines belonging to the pencil are rejected (colored green), because they do not match the measured transducer axis rotation. [Color version available online.]

To find the 2D image coordinates of the transducer tip axis, the Open Source Computer Vision Library (http://www.intel.com/technology/computing/opencv/) is used to automatically segment the transducer tip axis in the undistorted laparoscope images in real time. First, the Canny edge detection algorithm [25] is applied to provide a binary image of edges, which is fed into a Hough transform [23] to give a set of lines in the camera image. We obtain the end points of each line.

To find the two lines corresponding to the two edges of the transducer tip, the whole set of segmented lines is first back-projected into 3D space, i.e., each end point x_C given in image coordinates (pixels) is projected back to X_C given in camera coordinates (millimeters):where K is the 3 × 3 camera calibration matrix containing the principal point and focal length [17] and X_C lies on the image plane, i.e., Z_C = 1. Together with the camera center, each line represented by its two end points and defines a plane, which can be completely described by its unit normal .

As illustrated in Figure 3, all planes are now compared to the measurements of the transducer tip axis (which is defined by b_TipS and d_TipS in tip sensor coordinates; see the Transducer tip axis calibration section), acquired by EMT and transformed into camera coordinates:where

Figure 3. Back-projection of a segmented line and its comparison to the transducer tip axis measured by EMT. [Color version available online.]

is the transformation from the laparoscope OT body to the camera center, is the transformation from the world (OT) coordinate system to the laparoscope OT body, and is the transformation from the EMT transmitter OT body to the world (OT) coordinate system.

To obtain a unified representation of all planes, we adjust each of the respective normals n to point in the same direction as the vector defined by the cross product of d_C and b_C (see Figure 3), i.e., if n · (d_C × b_C) < 0, we will negate n.

The angle α between the measured transducer tip axis and each plane can be determined byThe distance d between the base point of the measured transducer tip axis and the plane is described byDepending on whether d is positive, negative, or zero, the base point b_C of the measured transducer tip axis will be above (on the half-space to which the normal is pointing), beneath, or on the plane.

For each line, |α| and |d| are compared to the thresholds α_thresh and d_thresh, respectively. If both parameters are below the corresponding threshold, it can be assumed that the current line corresponds to an edge of the transducer tip. To provide enough tolerance to compensate for erroneous EMT measurements, the thresholds are chosen in such a way that on the one hand segmented lines are selected which are definitely part of the transducer tip, and on the other hand lines are rejected which are actually part of the image background. We empirically determined values of α_thresh = 5 (degrees) and d_thresh = 30 (mm). These values gave a good balance between stability against distortions and the potential for additional error correction.

2. Correction transformation. To compute the final correction transformation, we analyze the previously evaluated set of lines belonging to the edges of the transducer tip, as illustrated in Figure 4. Iterating over all these lines, the distance d between the plane described by the back-projection of each line and the base point of the measured transducer tip axis is computed, and in both directions the greatest distance is stored. Because the sign of d is different for both directions, this is equivalent to storing the maximum negative distance d_negmax and the maximum positive distance d_posmax. Ideally, the absolute difference between these distances |d_posmax − d_negmax| is equal to the diameter of the ultrasound transducer tip, which is 10 mm. If this absolute difference stays within certain limits, e.g., 10 ± 2 mm, it can be assumed with high probability that lines were extracted which belong to both edges of the transducer.

Figure 4. Back-projection of four segmented lines, which generates four planes and their corresponding normals n₁, n₂, n₃, and n₄ (plane coloring according to Figure 2). For each plane j, its distance d_j to b_C and angle α_j to d_C are computed. We suppose that all four planes satisfy |α_j| < 5° and |d_j| < 30 mm. Because d₁ is the maximum positive distance from b_C, and d₄ the maximum negative distance from b_C, we can set d_posmax = d₁ and d_negmax = d₄. If |d_posmax − d_negmax| = |d₁ − d₄| stays within 10 ± 2 mm, we continue our computations. For all distances i unequal d_posmax and d_negmax, we check whether d_posmax − d_i < 2 mm or d_i − d_negmax < 2 mm. All planes not satisfying this criterion are excluded from further computations, as for plane 2 (blue). Using the remaining three yellow planes, a mean plane (red) defined by and is determined. The transducer tip axis can finally be translated along for d_est = 0.5(d₁ + d₄) mm and rotated by around . [Color version available online.]

Because of (for example) reflections on the transducer tip surface, there might be artifacts affecting lines across the tip, so we want to exclude lines that are not closely aligned with its probable edges. Thus, for the computation of the correction transformation we use information about lines within a certain maximum distance, e.g., 2 mm, from the outermost lines. This is the case for all lines i, where either d_posmax − d_i < 2 mm or d_i − d_negmax < 2. From these i = 1 … n lines we compute the mean plane normal and the mean angle between transducer tip axis and plane.

The distance d_est between the segmented transducer axis and the electromagnetically measured transducer axis can be estimated as the average of the minimum and maximum distances d_est = 0.5(d_posmax + d_negmax).

When translating the measured transducer tip axis along the mean plane normal by the estimated distance d_est, the axis origin will be in the middle of the segmented transducer tip. Next, the tip axis must be rotated into the plane. Since the rotation axis r has to be orthogonal to the plane normal as well as to the measured tip axis direction, it can be computed as . Together with the mean angle between the measured tip axis and plane, a homogeneous correction transformation can be estimated: The translation component along the mean plane normal can be calculated as and the rotation component can be computed from r and using Rodrigues' rotation formula [26]. This transformation maps the electromagnetically measured tip axis to a pose, from where it can be projected onto the image plane in such a way that it is exactly aligned with the segmented axis of the transducer tip.

Note that for the computation of the correction transformation we only used the original electromagnetic tracking measurements of the tip sensor and the laparoscope video as input into our algorithm for adjusting the axis alignment of the transducer tip. No initial correction is performed beforehand, e.g., by applying the redundancy-based method.

Experimental evaluation results

To reliably achieve meaningful results, all EMT measurements were acquired in a tracking volume of 20–36 cm for x, and ±15 cm for y and z, which has been verified by Ascension Technology Corporation for their microBIRD system [27] to yield the most accurate measurements for the sensors and transmitter used. We did not experience any difficulties at the borders of this volume, so we certainly expect our method to be applicable to larger volumes, especially since our artificially introduced distortions should by far outweigh any inaccuracies that may arise from exceeding the optimal tracking volume.

Error detection

To estimate the laparoscope augmentation errors automatically, an additional OT body (“tip body”) was temporarily attached to the transducer tip and co-calibrated to the tip sensor by another hand-eye calibration (see System calibration section and Figure 5). One marker of the tip body was chosen as a reference and automatically segmented whenever visible in the laparoscopic video. We compared its center coordinates to the projection of its respective OT coordinates onto the image plane. The corresponding EMT measurements, as well as their approximated corrections, were projected using the previously determined hand-eye calibration transformations.

Figure 5. Setup for error evaluation.

Figure 6. ROC curves for error prediction. (a) Prediction of an error of 5.0 mm or greater. (b) Prediction of an error of 7.5 mm or greater.

Evaluation data was recorded using a laparoscope-to-marker distance d_{lap_to_m} of 5 to 10 cm, which is a typical intraoperative working distance. The current distance can be recovered from OT data and the camera calibration parameters, and thus from the position m_C of the marker with respect to the camera coordinate system. m_C can be computed similarly to equation (7) bywhere is the transformation from the laparoscope OT body to the camera center, is the transformation from the world (OT) coordinate system to the laparoscope OT body, and m_OT is the current position of the marker with respect to the world (OT) coordinate system. The current laparoscope-to-marker distance d_{lap_to_m} can now be determined from m_C by simply computing its norm: d_{lap_to_m} = ‖m_C‖.

We also used this information to scale pixel units to millimeters. The distance in pixels from the projected OT marker center to the camera center can be computed from the in-plane distance to the principal point as follows:where and are the distances of the projected OT marker center from the principal point in the x and y direction, respectively, and is the focal length in pixels. As our laparoscope camera has nearly square pixels, can be defined as the mean between the focal lengths given in the x and y direction. The current ratio between millimeter units (referring to the spatial position of the marker) and pixel units (referring to its position in the image plane) can then be computed as .

For each of six evaluation series, the transducer was fixed at a different pose and the laparoscope was used to measure the projected distances from five differing poses, each in an undistorted and a distorted environment. To distort the EMT field, two alternative approaches were evaluated: A metal plate was placed on the table to simulate primarily static distortions caused, for example, by an operating table. For dynamic distortions, a steel rod of diameter 10 mm was brought close to the transducer to simulate a surgical instrument, its proximity and angle to the transducer being changed in five measurements.

To evaluate our distrust function statistically, we computed the distrust level (cf. equation (2)) for each of the poses. An offset between the segmented marker and the EMT projections of more than 2 mm was regarded as erroneous measurement. In this case, we expect a distrust level δ of more than δ_thresh (during hand-eye calibration, δ_thresh was empirically determined to be 20). We defined the following cases for our evaluation:

• A true positive is a measurement in which the EMT error was above 2 mm with a distrust level above 20 – the detector rejected an erroneous reading correctly.

• A true negative is a measurement in which the EMT error was below 2 mm with a distrust level below 20 – we correctly accepted the original EMT data.

• A false positive (type 1 error) is a measurement in which the EMT error was below 2 mm, but the distrust level was above 20 – we were unable to detect a correct value and rejected it without necessity.

• A false negative (type 2 error) is a measurement in which the EMT error was above 2 mm, but the distrust level was below 20 – the record was accepted although the real error was large.

The results are listed in Table I. In approximately 85% of all cases, we correctly detected the true situation (true positives and true negatives).

Table I.  Distortion detection rate by our distrust level without distortion, with static, and with dynamic field distortion.

Distortion		True	False
Without	positive	40.0%	10.0%
	negative	30.0%	20.0%
Static	positive	100.0%	0.0%
	negative	0.0%	0.0%
Dynamic	positive	73.8%	13.8%
	negative	12.4%	0.0%
Average	positive	71.3%	7.9%
	negative	14.1%	6.7%

Receiver operating characteristics. Additionally, for our set of distorted measurements we computed several receiver operating characteristics (ROC) for predicting errors between 2.5 mm and 10 mm. ROCs have the benefit of considering not just a single, possibly manually chosen threshold, as in the evaluation above, but the whole range of possible thresholds. They therefore extend the analysis of our error prediction performance.

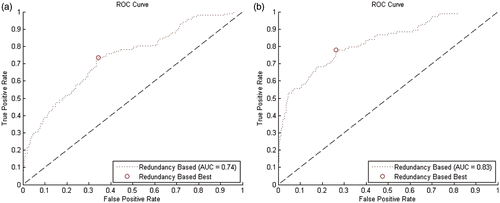
Our error prediction algorithms compute a distrust level for each measurement, and using this distrust level the measurement can be considered as either correct or erroneous in comparison to a selected threshold δ_thresh. The computation used to determine the distrust level remains fixed, but, according to the selected threshold, various rates of false positive or false negative decisions can be achieved. An ROC curve visualizes the interdependence between low false-positive and low false-negative rates, displaying all possible trade-off results based upon all possible thresholds. The performance of our redundancy-based method for classifying measurements of the flexible tip sensor position is shown in Figure 6.

A key metric for evaluating ROCs commonly used in statistics is the Youden index [28], which is defined as follows:where a is the fraction of true positives, b the fraction of false negatives, c the fraction of false positives, and d the fraction of true negatives. The possible range of values is from zero to one inclusively. In Figure 6, we also marked those values with the maximum Youden index, because those can be considered to yield the best trade-off. Depending on the application, other values might be favored, i.e., if low false-positive rates are favorable over low false-negative rates or vice versa.

In addition to the figures, we also present the key values for each ROC in Table II. For both algorithms we give the area under the ROC curve (AUC) and the maximum Youden index J_max. For J_max we also give the corresponding threshold value δ_thresh, sensitivity (= true positive rate, TPR) and specificity (SPC), and both the smallest false-positive value FP_min and the greatest false-negative value FN_max are given. FP_min and FN_max are the most extreme case where our method would have led to a wrong classification.

Table II.  Receiver operating characteristic key figures for prediction of distortion errors of at least 2.5, 5, 7.5, and 10 mm.

	AUC	Jmax	δthresh	TPR	SPC	FPmin	FNmax
2.5 mm	0.65	0.24	6.26	0.91	0.33	0.84	6.44
5.0 mm	0.74	0.39	11.34	0.74	0.66	0.84	13.69
7.5 mm	0.83	0.52	13.98	0.78	0.74	0.85	13.69
10.0 mm	0.86	0.67	27.75	0.72	0.94	0.88	14.29

The redundancy-based prediction of an error of 5 mm or greater would have achieved a sensitivity of 74% and a specificity of 66% in the best case, i.e., it would have correctly predicted 74% of all errors of 5 mm or greater and 66% of errors below 5 mm. For the prediction of an error of 7.5 mm or greater, sensitivity and specificity of our method would have been 78% and 74%, respectively. For the remaining values, including those for 2.5 mm and 10 mm, see Table II.

Error correction

For assessing the overlay accuracy in both the undistorted and distorted case, the ultrasound transducer was fixed in various poses and the laparoscope was used to observe the transducer tip from various angles and distances.

In the course of these experiments, the transducer tip was steered to different angles and the laparoscope was also rotated around its own axis. To distort the magnetic field we again used the steel rod with a diameter of 10 mm.

For each measurement, the uncorrected position of the flexible tip sensor, the tracking redundancy-based corrected position of the flexible tip sensor, and the vision-based corrected position of the flexible tip sensor were transformed using the transformation from the flexible tip sensor to the flexible tip OT body. The resulting positions were then projected into the image plane, the spatial location of which was known from camera calibration. Also, the measured 3D position of the flexible tip body (centered in one of the markers) was projected into the image plane. The distance in millimeters within the image plane to the segmented midpoint of the OT marker was computed and taken as a measure for the overlay accuracy.

Only measurements within a distance of 5 to 20 cm between the OT marker and the camera center were accepted. This rather large distance of up to 20 cm is required in order to observe both the transducer tip (for axis segmentation) and the marker at the same time. Maintaining such a large distance is, however, very unlikely during surgery, and the laparoscope was thus calibrated to be most accurate for a maximum working distance of approximately only 10 cm. This reduces the overlay accuracy when the laparoscope is more than 10 cm away, so theoretically the results obtained here could be further improved.

To assess the overlay accuracy of the two error correction methods we took 207 undistorted and 935 distorted measurements. We projected the target point onto the image plane using the OT alone (projected OT), the EMT alone (projected EMT), the combined OT and EMT (redundancy-based correction), and the correction using the image information (vision-based correction), and computed its distance to the centroid of a marker segmented in the image.

For the results in both undistorted and distorted cases see Table III, where we computed the minimum (Min), maximum (Max), mean, and root mean squared (RMS) errors and their standard deviation (SD). As illustrated, the simple tracking redundancy-based error correction, as well as the vision-based error correction approach, yielded improvements over the uncorrected flexible tip sensor. In both undistorted and distorted environments, the vision-based method is superior to the redundancy-based method.

Table III.  Overlay errors in an undistorted and a distorted field.

	Min	Mean	SD	RMS	Max
Undistorted (mm)
Projected OT	0.11	2.67	1.38	3.00	7.57
Projected EMT	0.17	3.57	2.49	4.35	11.81
Redundancy-based correction	0.38	3.73	1.99	4.23	11.19
Vision-based correction	0.20	2.91	1.75	3.39	9.51
Distorted (mm)
Projected OT	0.05	1.81	1.02	2.08	6.10
Projected EMT	0.11	10.03	7.81	12.71	39.84
Redundancy-based correction	0.07	8.55	7.63	11.45	36.66
Vision-based correction	0.17	7.77	6.60	10.19	38.43

Exemplary application: Ultrasound augmentation

Ultrasound calibration. For the determination of the pixel scaling of the ultrasound B-scan plane and its transformation to the tip sensor frame, a single-wall calibration is performed [20]. Instead of scanning the planar bottom of a water bath, we scan a nylon membrane stretched over a planar frame, as proposed by Langø [29].

After acquiring 40 tip sensor poses and their corresponding lines that were automatically detected in the B-scan images, the calibration matrix was computed using the Levenberg-Marquardt optimizer. To determine the ultrasound calibration accuracy, a single EMT sensor with tip coordinates given in the EMT frame was submerged in the water bath. Its tip was segmented manually in 5 regions of the B-scan plane, which was repeated for 4 poses of the transducer differing from the ones used during calibration. The tip coordinates were transformed into the B-scan plane coordinates and compared to the segmented tip coordinates (scaled to mm). An RMS error of 1.69 mm with standard deviation of 0.51 mm and maximum error of 2.39 mm was obtained.

Visualization of the detected EMT error. To visually inspect the overlay of the B-scan plane on the laparoscopic live video, we constructed a cylindrical phantom containing straight wires which extend through the walls of the phantom. This was filled with water of known temperature. Adjusting the pixel scaling factors to an adequate speed of sound, the B-scan plane was augmented, allowing the camera to view a wire on the augmented plane and its extension outside the phantom walls. A typical augmented laparoscope image can be seen in Figure 7.

Figure 7. Ultrasound plane augmented on the laparoscope video – the red line is added manually to show the extension of the straight wire, which matches its ultrasound image. [Color version available online.]

Whenever the occurrence of an error is determined, it is shown by drawing a red frame around the ultrasound plane. Otherwise, the frame is drawn in green. An attempt to correct the error can be shown in yellow. The supplementary video demonstration (http://campar.in.tum.de/files/publications/feuerste2007miccai.video.avi) summarizes the results of all the experiments and allows the observer to qualitatively evaluate the performance of automatic distortion estimation.

Discussion

The flat tablet transmitter recently presented by Ascension Technology Corporation may be an alternative means of overcoming field distortions caused, for example, by the operating table. However, because of its lower excitation, in the same setup it performed worse than the mid-range transmitter for ultrasound calibration, resulting in errors of approximately 4-8 mm. Larger sensors could be used to improve the accuracy, but this would probably require larger trocars. Using 1.3-mm sensors, the total diameter of the laparoscopic transducer is only 11.8 mm (including the sterile cover), so it would still fit a regular 12-mm trocar.

Conditions in laparoscopic gastrointestinal surgery differ from those encountered in neurosurgery or orthopedic surgery, for example. Generally, it is sufficient to distinguish between structures of approximately 5 mm in size. For instance, canalicular structures such as bile ducts and vessels can be considered relevant and critical if they are at least 5 mm in size, and lymph nodes are suspected to be tumorous if they are at least 10 mm in diameter. Therefore, an error of approximately 2-3 mm, as obtained for the distortion-free environment, is acceptable for clinical conditions. Errors of more than 2 mm are successfully detected by our system in most cases.

As an alternative to the error correction methods presented here, all possible transducer tip movements can be modeled relative to the shaft body to correct the tip sensor measurements. This model-based error correction method is not, however, the focus of the present paper; it will be described in a future publication from our group.

In comparison to a model-based correction, the advantages of the vision-based correction method proposed here are that no assumptions are necessary concerning the internal configuration of the transducer or any calibration thereof. However, for accurate overlay purposes, a calibration of the extrinsic and intrinsic camera parameters of the laparoscope should be readily available. The imposed constraints of transducer tip size or shape (cylindrical with a diameter of 8-12 mm) should be applicable to a wide range of transducer models without the need for further modification.

Conclusion

We have presented new methods for detecting EMT tracking errors online and partially correcting these errors using a magneto-optic tracking setup. We have improved the state of the art [1], [6] for augmenting laparoscopic ultrasound images directly on the laparoscopic live images to give surgeons a better understanding of the spatial relationship between ultrasound and camera images. The laparoscopic ultrasound transducer tip is flexible. Therefore, our method could be applied to a larger set of applications. We are using two attached sensors, and are thus also able to provide a distrust level for the current EMT measurements. The system is therefore able to automatically update and warn the surgical staff of possible inaccuracies.

Declaration of interest: The authors report no conflicts of interest. The authors alone are responsible for the content and writing of the paper.