Needle-tissue interaction modeling using ultrasound-based motion estimation: Phantom study

Abstract

Needle insertion simulators find use in a number of medical interventions, such as prostate brachytherapy. A needle insertion simulator has three main components: the needle model, the tissue model, and the model of interaction between the needle and the tissue.

In this paper, a new methodology is introduced for the joint modeling of tissue and needle-tissue interactions. The approach consists of the measurement of tissue motion using ultrasound, and of the needle position and base force. Tissue motion is determined using a correlation-based algorithm that processes the ultrasound radiofrequency data. The tissue elastic parameters and the parameters of the tissue-needle interaction model are determined by using numerical optimization to match the response of the needle insertion model to the measured data.

Phantom experiments were carried out in which a brachytherapy needle was inserted into a two-layer non-homogeneous phantom mimicking a prostate and its surrounding tissue. Experimental results show good agreement with the model obtained. In particular, the parameters of a three-parameter force model were identified for each layer of the phantom to fit the measured force to the simulated one. Also, the Young's modulus of each layer was identified to match the measured and simulated nodal axial displacements. This is the first report of the use of ultrasound radiofrequency data to characterize tissue motion during needle insertion. As the method is non-invasive and does not involve ionizing radiation, its application in patient studies is feasible.

• Needle insertion
• tissue deformation
• ultrasound imaging
• tissue modeling
• finite element method
• prostate brachytherapy

Introduction

Advances in medical robotics during the last decade have contributed to the widespread application of robots in surgical procedures [1]. The use of robotics for percutaneous needle insertion and guidance has been proposed by several groups (see, for example, references [2–5]). There has been extensive research in the use of robots for prostate brachytherapy, a treatment for localized prostate cancer in which a number of radioactive capsules (seeds) of ¹²⁵I or ¹⁰³Pd are delivered to the prostate and peri-prostatic tissue using long needles. The seed positions are carefully planned in the pre-operative stage so as to maintain a level of radiation sufficient to kill cancerous cells while delivering only a tolerable dose to the urethra, rectum and bladder. During the operation, the physician inserts the needles with the aid of a guiding grid. This grid allows the needle to move in parallel to the trans-rectal ultrasound (TRUS) probe axis (see Figure 1). Trans-rectal ultrasound and real-time X-ray fluoroscopy are used for image guidance during the operation.

Figure 1. Needle insertion during prostate brachytherapy. [Color version available online.]

The needle insertion forces deform and displace the prostate [6], and these deformations and displacements may lead to misplacement of seeds, resulting in treatment errors (over-dosed or under-dosed areas) and complications (impotence or urinary incontinence [7], [8]). Taking the tissue deformation into consideration during needle insertion requires considerable experience and skill on the part of the physician, and therefore extensive training. Needle insertion simulators can be used for physician training, path planning and robotic insertion.

Recently, a number of needle insertion simulators have been developed [9–11], as well as path planners [12–17] and robots for inserting the needle automatically [2], [3], [18] or assisting the physician in orienting the needle before manual insertion [4], [5], [19], [20]. A needle insertion simulator has three major components: a deformable model to simulate tissue deformation; a model to simulate the needle bending if the needle is flexible; and a needle-tissue interaction model to combine the needle and tissue models into one simulator.

The Finite Element Method (FEM) [21] is widely used to simulate tissue deformation during surgery [22] and needle insertion [11], [23–25]. Different flexible needle models have also been developed and used in path planning [13], [17], [26], [27].

This paper introduces a new method for studying and identifying a model of the tissue and the needle-tissue interaction. Needle-tissue interaction models have been studied extensively [23], [28–32]. Okamura et al. divided the force during insertion of a needle into a bovine liver into three components: a force due to the capsule and organ stiffness, modeled by a non-linear spring; a friction force, modeled by a modified Karnopp model; and a cutting force occurring at the needle tip, modeled by a constant force dependent on a particular tissue property [28]. The model parameters were identified using the needle insertion force, without measuring tissue displacement. The needle tip and friction forces applied by a needle during insertion into a canine prostate were reported by Kataoka et al. [29]. A patient- and procedure-specific model was devised by Podder et al. to predict the maximum force that is applied to a needle during insertion into the prostate and perineum [30]. A Best Linear Unbiased Estimator (BLUE) was used for this purpose. The patient-specific parameters in the model were age, body-mass index, ethnicity, prior treatment, stage of cancer, prostate-specific antigen (PSA) level and Gleason score, while the procedure-specific ones were needle diameter and average needle insertion speed and acceleration. The insertion force data collected during brachytherapy of 25 patients were used to identify the model coefficients.

Another approach to modeling the needle-tissue interaction is to combine the measurements of tissue deformation with measurements of needle insertion forces. Tissue deformation can be measured with different modalities and is used to identify the model parameters. DiMaio and Salcudean used this approach to model the needle-tissue interaction during insertion of a needle into a PVC phantom [23]. They measured the tissue deformation by tracking several tissue surface markers in two dimensions using a video camera. The force and displacement data were incorporated through a non-linear finite element model for the tissue phantom. The elastic properties of this phantom were identified prior to the experiment. They introduced a force model with a peak force density at the needle tip followed by a constant force density along the rest of the needle shaft. In order to be used in a simulator, the force density was integrated with a stick-slip model [33]. The stick-slip interaction method was later used in several other studies [11], [14]. Crouch et al. extended this work to three dimensions [32]. They implemented a grid of fiducials inside a homogeneous silicon gel tissue phantom and measured their displacements in three dimensions during the needle insertion, using a stereo video camera system. The tissue phantom was transparent to enable the video cameras to track the implanted markers. A linear finite element analysis was carried out to identify the force model parameters from the force and displacement data. This group introduced a force model composed of a peak force density near the needle tip followed by a dip and then a constant force density along the shaft. They also studied the velocity dependency of these parameters and the effects of tissue relaxation. Hing et al. implanted several fiducial beads inside tissue and measured their displacement during insertion using a dual C-arm fluoroscope system [24]. They identified a local effective modulus for the tissue before puncture and an approximate cutting force for soft tissue samples.

In this paper, a new experimental method is introduced to model needle-tissue interactions. In this approach, ultrasound (US) radiofrequency (RF) signals are used to measure the tissue displacements [34], [35]. The needle position within the tissue, the needle base force, and the tissue deformation measurements are combined to identify the force distribution parameters for a two-layer phantom using a linear finite element model. The elastic moduli of the layers are identified at the same time. In contrast to other studies, US imaging enables us to measure the internal tissue motion without implanted markers. Furthermore, US imaging is a common imaging modality in many image guided interventions, including biopsies and prostate brachytherapy, so this method is easily adaptable to patient studies. Previously, Langevin et al. [36] used RF signals to measure tissue displacements during acupuncture. However, they did not derive a needle-tissue interaction model.

To demonstrate the feasibility of our method, we carried out experiments with a prostate phantom. A brachytherapy needle was inserted with controlled speed into a non-homogeneous, non-transparent two-layer prostate phantom with unknown elasticity parameters. Using the recorded needle position and base force and the tissue displacement estimates obtained from RF signals, a finite element model was used to identify the force model parameters and elastic moduli jointly from a single insertion.

The next section begins with details of the experimental setup designed to insert the needle into the tissue phantom and collect data. This is followed by a description of the phantom, an introduction to the tissue displacement measurement method, and a description of its experimental validation. Next, a three-parameter needle shaft force distribution model is introduced, followed by descriptions of the parameter identification algorithm and the simulation method employed. The subsequent sections present the experimental results and discussion, followed by conclusions and a note on possible avenues for future work.

Materials and methods

Experimental setup

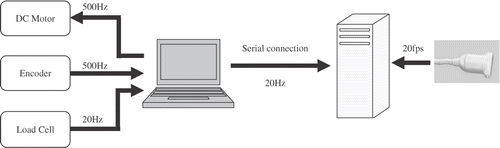
In order to insert the needle into the phantom and measure the insertion forces and tissue displacements, a translational lead-screw stage equipped with a load cell was used to insert an 18-gauge brachytherapy needle (Bard, Murray Hill, NJ) into a prostate phantom with controlled speed. The linear stage was powered by a Maxon DC motor with an optical encoder. The stage and motor combination has a resolution of approximately 1 µm. A proportional controller was used to control the heavily geared DC motor at a rate of 500 Hz. The needle insertion force was measured via a load cell (MBD-2.5, Transducer Techniques, Temecula, CA) mounted at the base of the needle.

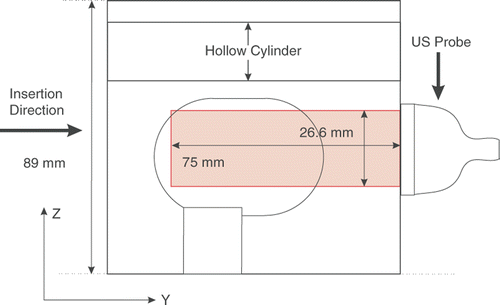
B-mode images and digitized radiofrequency signals were recorded simultaneously using a Sonix RP PC-based ultrasound machine and an L12-5 38-mm linear probe (Ultrasonix Medical Corporation, Richmond, British Columbia, Canada) mounted at the back side of the tissue phantom. The experimental setup and the position of the probe can be seen in Figure 2. The ultrasound machine recorded the RF data at 20 frames per second (fps). The computer that controlled the insertion speed also transmitted the encoder and load cell data to the US machine PC through the serial port connection at 20 Hz. The schematic diagram of the data flow between different devices is shown in Figure 3.

Figure 2. The experimental setup. [Color version available online.]

Figure 3. Schematic diagram of data flow in the experimental system.

Phantom design

A non-homogeneous phantom was constructed for the experiment. The phantom consists of an inclusion made of 100% polyvinyl chloride (PVC) plasticizer (M-F Manufacturing Co., Inc., Fort Worth, TX), a softer surrounding made of 66.7% PVC plasticizer and 33.3% plastic softener (M-F Manufacturing Co., Inc.), and a hollow cylinder. The phantom is shown in Figure 4. The harder inclusion is composed of a cylinder with a hemisphere at each end, connected to the base by another cylinder. The inclusion is designed to mimic the prostate and its rotation around the pubic bone, while the hollow cylinder is designed to simulate the rectum. During the experiment, a stiff cylinder was inserted inside this hole to mimic the effects of the trans-rectal probe on the motion of the prostate. To create enough scattering effect for US imaging, cellulose was added to the inclusion and the surrounding material.

Figure 4. The tissue phantom, showing the inclusion and the hollow cylinder. [Color version available online.]

It is important to choose the phantom material carefully, as needle friction forces and material brittleness vary significantly among materials having similar Young's moduli. PVC was chosen over agar and bovine gels as it produces needle forces closer to the insertion forces perceptible during brachytherapy (forces recorded during brachytherapy are reported in reference [37]). Commonly used agar (1–3% agar added to water) and bovine gels (up to 20% gelatin added to water) create very small needle insertion forces compared to PVC. The needle insertion forces for agar, gel and PVC tissue phantoms with variable compositions are reported in reference [38], which shows that the insertion force for PVC is significantly higher than those for the strongest agar or gelatin phantoms. In addition, since the tissue displacement algorithm used in this work is based on US imaging, the quality of US images directly affects the outcome of the algorithm. PVC materials with added cellulose yield US images of higher quality than those obtained using the other materials.

Tissue displacement measurement

The phantom was imaged to a depth of 75 mm using a linear-array probe with 128 elements. The line density and sector were set to 256 and 70%, respectively, to capture RF frames with 178 lines in the lateral direction and a density of 6.7 lines per millimeter. The transmit center frequency was set to 5 MHz and digitized at 40 MHz, and the echo signals were captured at 20 fps. The RF signals were up-sampled with a factor of two to increase the accuracy of the estimation algorithm. The relative positions of the ultrasound probe and imaging plane with respect to the tissue phantom are shown in Figure 5.

Figure 5. Cross section of the tissue phantom, showing the position of the probe and the US imaging plane.

The recorded data were processed off-line using a normalized cross-correlation-based time delay estimator. To reduce the computation time, the standard algorithm was replaced with the time delay estimator with prior estimates (TDPE) [34], [35]. TDPE works similarly to the standard algorithm but reduces the size of the search region by predicting the motion using previous estimates. To ensure that the prediction will not result in losing track of motion, TDPE also monitors the corresponding correlation coefficients. If the estimation based on the prediction results in poor correlation coefficients, the prediction is ignored and a standard cross-correlation algorithm over a larger search region is used to recover the actual displacement. To process the data, each RF line was divided into 120 overlapping windows with axial length of 1 mm each (52 samples). A portion of a typical RF line and three overlapping windows are shown in Figure 6. To reduce the bias and variance introduced by finite sampling intervals, sub-sampling using a cosine fit was used in both directions [39]. The axial and lateral components of the displacements (along the y and z axes according to Figure 5) between the reference and displaced frame were estimated using TDPE. Initially, the first frame was set as the reference frame. To compensate for the de-correlation caused by the large displacements and deformations, a dynamic reference update method was used. In this method, every time the average cross-correlation value corresponding to the latest simulated displacement dropped below a threshold (e.g., 0.95 in this study), the reference frame was replaced with the latest frame. Therefore, despite the deformation in the tissue, the deformation between each window and its corresponding window in the last reference frame was small. Using this algorithm, the absolute displacement for every spatial location was the sum of the relative displacement of the current location from the corresponding location in the last reference frame plus the displacement of the current reference frame from the initial frame.

Figure 6. A portion of a normalized RF line and three overlapping windows.

TDPE validation

An independent experiment was conducted to validate the accuracy of the TDPE algorithm in measuring phantom material displacement. In order to be able to measure the material displacement with another device and compare it to the TDPE results without the addition of markers, a known rigid motion was applied to the material with respect to the probe. The ultrasound probe was mounted on the lead-screw stage that provides controlled motion for the probe. In addition, the tissue phantom was placed inside a box, the front side of which was closed with a thin layer of wrapping plastic. The box was filled with water, and the probe was in contact with the plastic membrane in front of the box (see Figure 7). In this configuration, a layer of water and a thin plastic membrane separated the probe from the tissue phantom. Therefore, the probe was able to move axially without deforming the tissue phantom, causing a relative rigid motion for the tissue phantom in the opposite direction. The probe was moved axially in sinusoidal paths with variable amplitudes and frequencies, while the tissue was imaged at 20 fps. The displacement of the phantom material within a region of interest was measured using TDPE. Since the motion was rigid, the displacement within this region of interest was spatially constant. The probe position was measured by the encoder and was considered as the real displacement. Figure 8 shows the recorded probe position and the average tissue displacement in the region of interest. The maximum average and standard deviation of the error are summarized in Table I, showing the accuracy of the TDPE method.

Figure 7. The schematic of the setup used for TDPE validation. The tissue phantom is in a box filled with water. The probe motion is not transmitted to the tissue phantom due to the presence of water between them.

Figure 8. The probe motion and estimated tissue displacement for different frequencies and amplitudes. In each case, the blue broken line represents the probe position and the solid red line represents the average tissue displacement in the region of interest. [Color version available online.]

Table I.  Validation results for TDPE.

Frequency (Hz)	0.25	0.25	1.0	0.25–2.5
Amplitude (mm)	1.0	2.0	1.0	0.5
Max. avg. error (mm)	0.08	0.15	0.4	0.15
Max. Std error (mm)	5e-3	0.03	0.025	0.019

Force and displacement measurement

During the experiment, the needle was inserted using the linear stage with a controlled position along the y axis, as shown in Figure 9a. To avoid the deteriorating effects of the metallic needle on the ultrasound images and increase the accuracy of the tissue motion-tracking algorithm, the needle was inserted 5 mm out of the US image plane. The tissue phantom was meshed with 4-node tetrahedral elements to be used in a finite element analysis. The axial and lateral displacement of the mesh nodes located in the US image plane were measured with TDPE and are reported in Figures 9c and 9d. The lateral motion estimates are insignificant compared to the axial motions. In addition, the resolution of the lateral motion estimation is one order of magnitude lower than the resolution in the axial direction. Therefore, the accuracy of the lateral motion estimation can be low, especially when the lateral motion is less than a line's width. As a result, in the rest of this study, only the axial motion estimation was used for modeling. The axial insertion force applied to the needle during the insertion is shown in Figure 9b. A needle base force equal to zero after t = 118.5 s indicates the full retraction of the needle. However, the tissue displacement measurements show an average displacement of 0.5 mm after the full retraction in Figure 9c. This error may result from the accumulation of residuals caused by the dynamic frame update method, slight rigid movement of tissue during retraction of the needle, and minor topological changes in the tissue caused by the needle. As can be seen in Figure 9a, the needle motion has two stop-periods. Relaxation effects in the tissue can be seen as a decrease in force and displacement during these two periods. Dealing with the viscoelastic properties of tissue is beyond the scope of this paper and is the subject of further research. The needle was partially retracted and inserted after each stop. Since the needle was inserted again along the same path, tissue cutting did not occur to the same extent. Therefore, the second and third force peaks (at t = 60 s and t = 80 s) are smaller than the main force peak (t = 40 s).

Figure 9. (a) Needle tip position; (b) Measured insertion force; (c) Axial displacement of the mesh nodes located in the US imaging plane; and (d) Average lateral displacements of the nodes above and below the needle. The needle was partially retracted and inserted again after the main insertion. Since in the second and third insertions the needle was inserted along the same path as in the first insertion, less tissue cutting occurred. Therefore, the second and third peak forces (t = 60 and 80 s) are smaller than the first one (t = 40 s). [Color version available online.]

Needle shaft force distribution

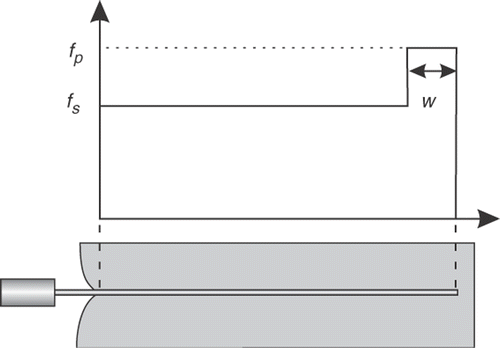
The needle base force during penetration (t ≤ 40 s) consists of four regions which are marked in Figure 9b. Knowing that the tissue phantom has two components, these four regions can be reduced to two major components: regions 1 and 3 belong to a tissue puncturing phase, while regions 2 and 4 occur after puncturing and can contribute to normal penetration. Inspired by the shape of the needle base force and the model introduced in reference [23], a three-parameter force distribution – two consecutive pulses with variable amplitude and extent – was adopted to model the needle-tissue interactions for each layer of the tissue. As shown in Figure 10, the model is composed of a peak force density near the needle tip f_p, a shaft force density f_s, and the width of the peak force density w. This model is identified to simulate the force during the main insertion phase (i.e., 0 ≤ t ≤ 40 s). The needle-tissue interactions during relaxation or retraction of the needle are not modeled.

Figure 10. The needle shaft force density.

Parameter identification method

The elastic properties of the tissue phantom were not known prior to the experiment. Therefore, in addition to the force model parameters, the elasticity parameters of the phantom material had to be identified. A finite element model was used to identify these parameters jointly through simulation. The tissue phantom was meshed for FEM simulation (see Figure 11). The needle tip position, the needle insertion force, and the axial displacement of the mesh nodes located in the US plane were fed into the identification algorithm as experimental data. Through successive simulations, the force model and elasticity parameters of the tissue phantom were identified in order to fit the simulated forces and displacements to the measured ones. The data from the main insertion phase were chosen for this purpose.

Figure 11. Tissue mesh with tetrahedral elements. [Color version available online.]

The measured displacement drift is less than 1 mm at t = 120 s. From the three sources suggested for this drift, the integration of residuals increases over time and the rigid movement of the tissue phantom during the retraction occurred after t = 40 s. Therefore, the drift in displacement during 0 ≤ t ≤ 40 s is assumed to be negligible compared to the extent of tissue material displacement in this period. The unknowns to be identified for each tissue phantom region are three parameters for the force model and two elasticity parameters (Young's modulus E and Poisson's ratio v, assuming a linear elastic behavior for the tissue phantom material). To simplify the identification, the Poisson's ratios were pre-assigned to decrease the number of unknowns to four for each layer of phantom. As shown in Figure 9b, the measured force in the main insertion phase should be divided into four regions. To clearly define the width and slope of the force in each of these regions, a piece-wise linear model was fitted to the measured force (see Figure 12). This model has seven parameters to be optimized. Four of these are the slopes of each region and the other three are the needle positions at which the transition from one region to the next occurs. These parameters were optimized using the Nelder-Mead method [40]. In the rest of this work, the force model parameters are optimized to fit the simulated insertion force to this model.

Figure 12. The measured force (red broken line) and the piece-wise linear model (solid blue line). [Color version available online.]

In the identification algorithm, an initial set of force model parameters and Young's moduli are given as the inputs to a needle insertion simulator. The needle insertion simulation is achieved using the given parameters and provides a needle base force and a set of nodal displacements. In an inner loop, the force model parameters are updated to match the simulated and measured insertion forces. To accomplish this, the parameter f_p for each layer of the tissue phantom is adjusted so that the slopes of the simulated forces in parts 1 and 3 closely match the slopes of the corresponding recorded forces (see Figure 12). The same procedure is applied to the parameter f_s to match the slopes of the recorded and simulated forces in parts 2 and 4. The parameter w for each layer of the tissue phantom is also adjusted so that simulated regions 1 and 3 have similar width to the corresponding regions in the measured force. The inner loop iterations are terminated when the error between simulated and measured forces is smaller than a threshold. The parameters f_p and f_s are rounded to the closest integer, since higher precisions did not show a significant effect on the results. In an outer loop, the Young's moduli are updated using the Nelder-Mead search algorithm [40]. The cost function to be minimized is:where and are the simulated and measured axial displacements of the mesh node i in the US plane, l is the needle tip position, and W(l) is a weight function that puts more weight on regions 2 and 4, since in this work the accuracy of simulation was more important during the normal penetration phase than during the puncture phase. The outer loop iterations were terminated when the size of the final triangle in the Nelder-Mead method [40] was sufficiently small. The final values for the identified Young's moduli were tested using perturbations to ensure they were to local minima.

Simulation method

The tissue phantom was meshed using 4,453 linear tetrahedral elements with 991 nodes, as shown in Figure 11. The linear finite element method with linear strain was used for the simulation. The tissue phantom was fixed at the back and the bottom, and the hollow cylinder surface was also fixed using a hard plastic bar. Therefore, mesh nodes located on these surfaces were assumed to be fixed boundary conditions. With these boundary conditions, the tissue cannot rotate or deform easily during needle insertion. It has been shown in reference [41] and elsewhere (e.g., reference [42]) that boundary conditions play a major rule in deciding whether non-linear models are necessary. If the tissue is confined and cannot undergo large deformations and rotations, the difference between linear and non-linear models is insignificant. Under these conditions, the use of an efficient linear finite element model does not compromise the simulation accuracy [41].

Due to the low speed of insertion, the simulation is performed in a quasi-static mode. The force profile shown in Figure 10 was implemented in the simulation. This profile was integrated on the part of the needle which was inside the tissue phantom. This part is shown as L in Figure 13. As can be seen, this part is measured in the deformed configuration. Therefore, at each iteration, L is part of the solution. Thus, an iterative method was used to integrate the force over the equilibrium length. To distribute the force on the mesh nodes in contact with the needle, the following procedure was used. The resultant force from integration of the force density from the needle tip to the first node was applied to the first node, and the integration result from the first node to the second node was applied to the second node. The same procedure was used to apply forces to the other nodes in contact with the needle. In this simulation approach the force boundary conditions are applied to the nodes; however, a needle may enter an element from any point on the surface of the element. Therefore, mesh adaptation [11] was used to increase the accuracy of the simulation. With mesh adaptation, every time the needle tip reaches the surface of an element, the closest node on that surface is relocated on the needle tip in the undeformed mesh. The stiffness matrix is updated using the Woodbury matrix identity to accommodate the topological change in the mesh with low computational costs [11]. No external force is applied to relocate the node, since the modifications are applied to the undeformed mesh. A force boundary condition is applied to every node in contact with the needle, in the axial direction of the needle. Two displacement boundary conditions are applied to the same nodes in the other two orthogonal directions to maintain the nodes on the needle.

Figure 13. The length L over which the force is integrated in the deformed configuration. The broken lines show the elements in the undeformed configuration. [Color version available online.]

Results

The identification method takes the measured needle force and nodal axial displacements as input data. In addition, the Poisson's ratio has to be set as a known parameter. Two values of Poisson's ratios – 0.45 and 0.49 – were considered for both the inclusion and the substrate. In the second case, with Poisson's ratio of 0.49, the tissue is nearly incompressible, which is one of the characteristics of real tissue [43]. The identified force model parameters and Young's moduli for each case are presented in Table II.

Table II.  Needle shaft force density and elastic parameters.

v	Tissue	fs(N/m)	fp(N/m)	w(mm)	E(kPa)
0.45	Inclusion	70	200	12.5	41.0
	Surrounding	61	168	2.5	8.5
0.49	Inclusion	69	206	12.0	24.0
	Surrounding	63	117	3.0	7.0

Figure 14 shows the measured and simulated needle base forces for both cases, while Table III presents the maximum mean and standard deviation of the errors in the prediction of the displacements as functions of time.

Figure 14. Simulated and measured needle forces for two different Poisson's ratios. [Color version available online.]

Table III.  Simulation errors.

v	Max. mean disp. error (mm)	Max. Std error (mm)
0.45	0.5	0.5
0.49	0.4	0.6

Figure 15 illustrates the simulated and measured position of the nodes located in the US plane in the deformed and undeformed configurations for v = 0.49. As can be seen, nodes closer to the needle show higher errors. This may be due to the higher displacements of these nodes.

Figure 15. Position of the nodes in the US field of view. Squares denote the original positions, stars simulated positions, and circles the positions measured with TDPE. The broken line shows the projection of the needle on the US plane. Only axial displacements are considered. The Poisson's ratio is 0.49. [Color version available online.]

Discussion

In this work, the force model parameters and the Young's moduli were identified jointly for a two-layer phantom using the experimental data from a single needle insertion. In the presence of several layers of tissue, the joint identification can be very complex due to the mutual effects of different layers of tissue on each other. However, for specific procedures such as brachytherapy, it will be useful to identify both the tissue model and the interaction model at the same time. Furthermore, the methodology introduced in this paper can be used to identify the force model parameters based on the availability of elasticity properties from other sources. The inner loop of the identification algorithm can deliver the force model parameters for many layers of tissue if the Young's moduli are known. It is therefore useful to identify tissue elasticity parameters independently, if possible. Research in the field of vibro-elastography is in progress to determine the elasticity parameters of the prostate and surrounding tissue [44].

The Young's modulus of the inclusion material was independently measured using rheometry and was between 30 and 36 kPa. The Young's modulus varies based on the heating and cooling procedure during PVC fabrication. It also changes with time after the fabrication. Note that the identified Young's moduli are not close to the real Young's moduli of the tissue. As shown in this work, the identified Young's moduli depend on the assumed Poisson's ratio. The mesh quality affects the accuracy of the identified parameters too. Large tetrahedral elements show over-stiffness, since they impose their constant strain field over a large volume of tissue [45]. A mesh with higher resolution can yield identified elasticity parameters with higher accuracy at the expense of higher computational burden. The minimization cost function can also change the identified parameters. As a comparison, the elasticity parameters in reference [46] were adjusted to fit the average of the simulated axial displacements to the measured ones. The identified parameters in that study are different from the results provided in the current paper. However, it should be noted that the ultimate goal of this work is to achieve accurate insertion force and tissue displacement prediction. Therefore, mechanically inaccurate values for Young's moduli are acceptable if they lead to accurate simulation of tissue deformations.

In the identification algorithm, the cost function in Equation (1) was used as a similarity measure. However, other similarity measurements can be used with the same method. The similarity measure in reference [46] was the average of nodal displacements. Since positive and negative errors can cancel each other in the average of nodal displacements, the simulated displacements in reference [46] have higher standard deviations of the errors.

A linear FEM model was used to increase the computational speed. However, it is possible to replace this linear model with a non-linear one without increasing the number of unknowns. As an example, the Lamé parameters (interchangeable with Young's modulus and Poisson's ratio) are the only parameters necessary to build the constitutive equations for neo-Hookean material models [47]. Therefore, such a model can replace the linear model if higher accuracy is necessary and computational time can be increased.

The tissue displacement estimation method was validated when the tissue motion was rigid. Although tissue deforms during needle insertion, the reference frame update algorithm was used to compensate for this deformation. The TDPE algorithm can be validated in the presence of deformation by tracking the position of several implanted beads and comparing the results with those obtained using other tracking methods.

Conclusions and future work

In this work, a new methodology for the investigation of needle-tissue interaction was introduced. In this approach, ultrasound radiofrequency data are recorded during the insertion and used for tissue displacement measurement. The tissue displacement data, together with the needle base position and needle insertion force data, are used to identify the parameters of a three-parameter force distribution along the needle. In this paper, these parameters were identified for a two-layer non-homogeneous PVC prostate phantom. The tissue phantom was composed of a harder inclusion mimicking the prostate surrounded by a softer tissue. The phantom was not transparent and had no fiducial beads or markers. Prior knowledge of the elastic properties of the phantom was not used to determine the needle-tissue interaction model. The Young's moduli of the tissue phantom were identified jointly with the force model parameters with the aid of a linear finite element simulation. The tissue phantom was meshed for this purpose and the displacements of the mesh nodes located in the US plane were measured using a cross-correlation method. In an inner loop the force model parameters were adjusted to match the simulated and measured forces, and in the outer loop the Young's moduli were adjusted to minimize the cost function in Equation (1). Two different cases with two different Poisson's ratios were assumed. The identified force parameters and elastic properties can be used to build a needle insertion simulator for physician training, path planning, and robotic insertion.

In this work, a linear probe was used to acquire the images during insertion. However, during the brachytherapy procedure a trans-rectal probe is used to image the prostate in the sagittal/parasagittal and transverse planes. Therefore, during brachytherapy, the major displacement of tissue can be best seen in the lateral direction of the US image, which has significantly lower resolution (by approximately one order of magnitude) than the axial motion estimation. The effect of this discrepancy in resolution on the model depends on the tissue properties and will be the subject of further research.

The proposed algorithm will be used with finer meshes to increase the accuracy of the identification. The inner loop of the suggested method should be combined with other tissue identification algorithms (e.g., vibro-elastography) to identify the force model parameters for real tissue with several layers. The visco-elastic properties of the tissue and their effect on the identified parameters will be investigated in the future. Effects of needle insertion speed on the force model will also be studied. The tissue and force model parameters were identified using a single insertion. Further validation to show the efficacy of the model in simulating tissue deformation and insertion force for other insertion trajectories is also part of the planned future work.

Acknowledgment

This work was supported by NSERC and CIHR.