On combining internal and external fiducials for liver motion compensation

Abstract

This paper presents an in-vivo accuracy study on combining skin markers (external fiducials) and fiducial needles (internal fiducials) for motion compensation during liver interventions. We compared the target registration error (TRE) for different numbers of skin markers n_s and fiducial needles n_f, as well as for different transformation types, in two swine using the tip of an additional tracked needle as the target. During continuous breathing, n_f had the greatest effect on the accuracy, yielding mean root mean square (RMS) errors of 4.8 ± 1.1 mm (n_f = 0), 2.0 ± 0.9 mm (n_f = 1) and 1.7 ± 0.8 mm (n_f = 2) when averaged over multiple tool arrangements (n = 18, 36, 18) with n_s = 4. These values correspond to error reductions of 11%, 64% and 70%, respectively, compared to the case when no motion compensation is performed, i.e., when the target position is assumed to be constant. At expiration, the mean RMS error ranged from 1.1 mm (n_f = 0) to 0.8 mm (n_f = 2), which is of the order of magnitude of the target displacement. Our study further indicates that the fiducial registration error (FRE) of a rigid transformation reflecting tissue motion generally correlates strongly with the TRE. Our findings could be used in practice to (1) decide on a suitable combination of fiducials for a given intervention, considering the trade-off between high accuracy and low invasiveness, and (2) provide an intra-interventional measure of confidence for the accuracy of the system based on the FRE.

• Image-guided systems
• tracking
• respiratory motion compensation
• internal fiducials
• external fiducials
• navigation
• deformation model
• interventional radiology

Introduction

The liver is one of the most common sites for metastatic disease, irrespective of the primary tumor. As many patients are not eligible for surgery, minimally invasive procedures such as radiofrequency ablation (RFA) and cryotherapy are emerging as important additional therapy modalities for the treatment of liver tumor [1]. These procedures rely heavily on image guidance for accurate placement of the instrument within the target area. In general, the needles can be placed under real-time image guidance (ultrasonography (US), fluoroscopy) or under magnetic resonance (MR) or computed tomography (CT) guidance [2]. Real-time imaging modalities can continuously visualize the instrument in relation to the patient's anatomy and at the same time capture tissue motion secondary to patient movement, respiration and cardiac motion. However, these modalities are not always available or sufficient for guiding the procedure (e.g., because the tumor is not visible in the image), while radiation dose concerns may prohibit their use. When sonographic placement is not possible, CT is often the method of choice. In this case, the operator has to “mentally” register the patient with the planning CT image acquired pre-interventionally in order to transfer the planned trajectory to the patient, which requires a lot of practice, especially when in-plane needle insertion is not possible. To reduce the risk of needle misplacement, the needle position is checked repeatedly in control CT scans, leading to high radiation exposure for the patient and long procedure times.

Computer guidance appears to be a solution to the problem, but clinically available navigation systems have only been designed for use with rigid structures, such as the skull or spine, where the target remains in a constant position relative to certain reference points. The liver, however, exhibits significant motion due to respiration [3]. To address this issue, several research groups are investigating methods for applying established guidance concepts to soft tissue (see references [4–9]). The proposed approaches differ mainly in the following aspects:

1. Tracking method: Most groups use optical [6–8] and/or electromagnetic [5], [6], [9] systems to continuously locate surgical instruments during an intervention. Optical tracking systems are highly accurate, but require an uninterrupted line of sight between the tracking system and the tracked sensors. Electromagnetic systems, on the other hand, are less robust and accurate, but allow for integration of the sensors into the tip of an instrument.

2. Registration: To visualize surgical instruments in relation to anatomical structures extracted from pre-interventional images, it is necessary to register the tracking coordinate system with the image coordinate system. To achieve this, the most common approach is to construct fiducials that can be located by the tracking system and that are clearly visible in the CT images. Prior to the intervention, these markers can be mounted on the skin of the patient (external markers) [5], [6], [8], [9] and/or be inserted into the liver (internal markers) [5], [7].

3. Motion compensation: The most common approach to compensating for organ motion is to apply respiratory gating techniques, which are based on the assumption that the liver re-occupies the same position at identical points in the respiratory cycle. By performing the intervention in full expiration or inspiration only, the liver can be approximated as motionless. Alternatively (or additionally), a real-time deformation model can be applied, which estimates the position of a target structure continuously from the positions of tracked fiducials [5], [11].

During CT-guided interventions, the proposed systems require the position of the liver during needle insertion to be identical to its position during the planning CT-scan acquisition. When breathing freely (as opposed to being ventilated), the patients must thus be able to accurately reproduce a specific state within the breathing cycle, which can be challenging - especially in stressful situations. To overcome this problem, we introduced a needle-based navigation system for CT-guided punctures of the liver [7] in which a real-time deformation model is used to continuously estimate the position of an initially determined target structure from a set of percutaneously inserted fiducial needles. The workflow is illustrated in Figure 1. We showed that three fiducial needles are significantly better than two in capturing the deformation of the liver over the entire breathing cycle [11]; however, this results in a high degree of invasiveness for the intervention.

Figure 1. Workflow for navigated needle placement. Prior to the intervention, a set of fiducial needles is inserted in the vicinity of the target. Next, a planning CT scan is acquired and a trajectory to the target is planned. Finally, the image coordinate system is registered with the tracking coordinate system based on the fiducial positions. During the intervention, the fiducial needles are continuously located by an optical tracking system and a real-time transformation is used to estimate the position of the target point accordingly. A suitable visualization scheme guides the physician towards the moving target. [Color version available online.]

To allow navigated liver punctures to be conducted during free breathing and at the same time minimize the invasiveness of the intervention, we propose combining external and internal fiducials, as well as using the tracking data to automatically detect those time slots during the intervention which match the pre-interventional state. This study was performed to optimize percutaneous liver interventions, but is also relevant in the context of motion compensation during radiotherapy treatment.

The remainder of this paper is structured as follows: In the next section we introduce the tools constructed for this study and describe our experiments in detail. We then present the results of the study and discuss our findings in the context of related work.

Material and methods

Tools

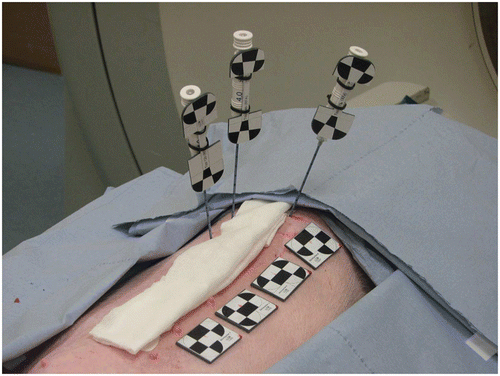
We used the MicronTracker 2, model H40 (Claron Technology, Inc., Toronto, Ontario, Canada), as the optical tracking system for this study. The following two tool types were designed (Figure 2):

1. Fiducial needles: Commercial RFA probes (LeVeen® CoAccess™ Electrode System; Boston Scientific Corporation, Marlborough, MA) equipped with printed target patterns which are localizable by the tracking system. The needles can be affixed firmly within the liver by means of the umbrella-shaped “anchors” (Figure 2).

2. Skin markers: Thin pieces of plastic with printed target patterns as recommended by Claron Technology.

Figure 2. Fiducial needle with extended soft tissue anchor and skin marker.

Data acquisition

This study was approved by the Committee for Animal Care and Research of the Karlsruhe Regional Council. Our experiments were conducted in two anesthesized, intubated swine. For each swine P_i (i = 1, 2), we examined three tool configurations Cj (j = 1, 2, 3), where each configuration represented an arrangement of three needles and four skin markers, as shown by way of example in Figure 3. For each configuration (P_i, C_j), we conducted the following workflow:

1. The skin markers S = {s₁, …, s₄} were attached to the skin of the swine, as shown in Figure 3.

2. Three needle-shaped tools N = {n₁, n₂, n₃} were inserted randomly into the liver such that the tracking system had an unobstructed view of all tools.

3. A CT scan was acquired to verify that all needles were placed inside the liver.

4. Beginning in full expiration, the tool positions were recorded over seven breathing cycles.

Processing of the recorded data for a given configuration (P_i, C_j) requires definition of a target needle n^target ∈ N, a set of fiducials F ⊂ N\{n^target} ∪ S, and a transformation type Φ_def ∈ {RIGID, AFFINE, TPS}, with TPS representing a thin-plate spline transformation.

Figure 3. Example of tool configuration.

To evaluate our methods on a maximum amount of data, we permuted the target needle and (if possible) the fiducials for the individual configurations. A set of experiments can be defined by three values: (n_f, n_s, Φ_def), where n_f < |N| = 3 denotes the number of fiducial needles used for the real-time computation and n_s ≤ |S| = 4 denotes the number of skin markers applied. As we can permute the target needle and the fiducials, we obtainnumber of experiments for the selected set, where n_c is the number of configurations.

Data processing

To process the recorded data for a given configuration (P_i, C_j), a target needle n^target, a set of fiducials F, and a transformation Φ_def, the following workflow was performed:

1. Initialization: The tip of n^target (which is extrapolated from the shaft position) was defined as the target. To store the initial positions of all tools, we extracted a set of landmarks from the first recorded sample: three landmarks from each skin marker and two landmarks from the axis of each fiducial needle. When only one fiducial needle (and no skin markers) was used for motion compensation, we added an additional landmark (extracted from the target pattern of the tool) because at least three landmarks are required. The original position of the target t⁰ was also stored. The deformation model Φ_def was then initialized with the original fiducial positions L⁰. Affine transformations and TPS were only applied for n_f · n_s > 0 to assure a robust registration.

2. Training: For each sample k within the first two breathing cycles, we extracted a set of landmarks representing the current positions of the fiducials. The deformation model was updated with L^k yielding the current transformation . For Φ_def ≠ RIGID we further computed a rigid transformation , mapping the original landmarks L⁰ onto the current landmarks L^k based on the least square method by Horn [10]. The associated FRE served as an indicator of the deformation of the tissue (FRE_rigid = 0: no deformation), and the entire data from the Training phase was then used to compute a threshold representing expiration:

3. Real-time estimation: The actual intervention was represented by the remaining five breathing cycles. For each sample k, the deformation model was updated with the current control point positions , yielding the current transformation . Next, FRE_rigid^k, the target displacement , and the TRE were computed with

For further analysis, we annotated each sample k with the corresponding state within the respiratory cycle state(k) ∈ {expiration, inspiration}. For this purpose, the median of was used as a threshold to classify the data, and the resulting binary curve was manually corrected by relabeling outliers (to obtain expiratory and inspiratory phases of reasonable duration). Finally, the following measures were computed from the values obtained in the Real-time estimation step:

ε_RMS: The root mean square (RMS) error in {TRE^k}

ε_RMS(exp): The RMS error in {TRE^k | state(k) = expiration}

ε_RMS(θ_rigid): The RMS error in {TRE^k |FRE_rigid^k < θ_rigid}

Results

The mean RMS TRE ε_RMS for different numbers of fiducial needles n_f ≤ 2 and skin markers n_s ≤ 4 during continuous breathing is shown in Figure 4. It can be seen that the TRE decreases drastically when combining fiducial needles and skin markers as opposed to using only one fiducial type. In fact, adding one fiducial needle to a set of skin markers led to an increase in accuracy of over 50% during continuous breathing. On the other hand, applying two arbitrarily placed fiducial needles for motion compensation, as opposed to just one, resulted in only a small difference.

Figure 4. Mean root mean square (RMS) target registration error (TRE) for different combinations of skin markers and fiducial needles averaged over all possible permutations in two swine (see Equation 1). The corresponding transformation was affine when both fiducial needles and skin markers were used and rigid otherwise. For n_f = n_s = 0, the RMS target displacement is shown. The corresponding transformation was affine for n_f > 0 and rigid otherwise (n_s = 4). [Color version available online.]

According to our results, the placement of the fiducial needles plays an important role. When n_f = 2 needles were arranged such that they enclosed the target in the craniocaudal direction (a placement strategy which we recommended in reference [11]), error dropped by 34% from 1.8 ± 0.9 to 1.2 ± 0.5 (affine transformation, n_s = 4). This, however, could also be due to the location of the target itself: we achieved error reductions of 12% and 20%, respectively, for n_f = 0, 1 when using as the target only the most centrally located needle within the liver (i.e., the one enclosed by the other two in the craniocaudal direction). In contrast, the location of the skin markers had no major effect on the accuracy, i.e., we obtained similar results when permuting the skin fiducials for a given n_s. According to Figure 4, the accuracy for n_s = 2, 3 and 4 skin markers was comparable.

Table I compares the performance of different transformation types for different numbers n_f of fiducial needles (n_s = 4). While affine transformations and TPS clearly outperform rigid transformations during continuous breathing, the transformations yield comparable results when applied at expiration only. The best respective mean RMS errors for n_f = 0, 1, 2 fiducial needles were 4.8 ± 1.1 mm, 2.0 ± 0.9 mm, and 1.7 ± 0.8 mm during normal breathing, which correspond to error reductions of 11%, 64% and 70%, respectively, compared to the case when no motion compensation is performed, i.e., when the target position is assumed to be constant. At expiration, the lowest errors for n_f = 0, 1, 2 fiducial needles were 1.1 ± 0.3 mm, 0.9 ± 0.2 mm, and 0.8 ± 0.2 mm, but no error reduction in general was achieved.

Table I.  Mean root mean square (RMS) TRE (in mm) for different transformation types and numbers n_f of fiducial needles during free breathing (ε_RMS) and at expiration only (ε_RMS(exp)) averaged over all possible permutations in two swine (see Equation 1). All skin markers were applied for motion compensation (n_s = 4). Note that affine transformations and TPS cannot be applied for n_f = 0 fiducial needles because the skin markers approximate a plane.

		nf = 0	nf = 1	nf = 2
εRMS	RIGID	4.8 ± 1.1	3.8 ± 1.1	3.4 ± 1.2
	AFFINE	–	2.0 ± 0.9	1.8 ± 0.9
	TPS	–	2.1 ± 1.0	1.7 ± 0.8
εRMS(exp)	RIGID	1.1 ± 0.3	0.9 ± 0.2	0.8 ± 0.2
	AFFINE	–	1.0 ± 0.4	0.9 ± 0.3
	TPS	–	1.0 ± 0.4	0.8 ± 0.3

In general, FRE_rigid correlated highly with the TRE (Pearson product-moment correlation coefficient; p < 10⁻²). Furthermore, we obtained similar results for the manually labeled states representing expiration and those classified automatically, as shown in Figure 5. It should be pointed out that (apart from several outliers) the automatically generated gating curves were identical to the manually generated ones. Figure 6 exemplarily visualizes the TRE, the target displacement δ_target, and the FRE_rigid over four breathing cycles for different numbers of fiducial needles.

Figure 5. Mean root mean square (RMS) target registration error (TRE) for different numbers of fiducial needles during continuous breathing (TRE), at expiration (TRE(exp)) and with automatically detected favorable time slots based on FRE_rigid (TRE(T_rigid)), as described in the Data processing section, averaged over all possible permutation in two swine (see Equation 1). The corresponding transformation was affine for n_f > 0 and rigid otherwise (n_s = 4). [Color version available online.]

Figure 6. Sample diagrams showing the TRE, the target displacement and the FRE of the associated rigid transformation (FRE_rigid) over four breathing cycles for different numbers of fiducial needles n_f ∈ {0, 1, 2}. [Color version available online.]

Discussion

We investigated combining external and internal fiducials for real-time motion compensation during liver interventions. We compared the TRE in vivo for different numbers of skin markers n_s and fiducial needles n_f, as well as for different transformation types. During continuous breathing, n_f had the greatest effect on accuracy, and both affine transformations and TPS outperformed rigid transformations. In contrast, we obtained comparable results for various settings at expiration. The results of this study can be used in practice to choose an appropriate set of fiducials for a given intervention, considering the trade-off between high accuracy and low invasiveness. Furthermore, our data showed that the FRE of a rigid transformation reflecting tissue motion (FRE_rigid) generally correlates highly with the TRE and can thus be used intra-interventionally as a measure of confidence for the estimation accuracy of the system.

Soft tissue navigation with internal markers is gaining increasing attention in the literature. One of the first motion compensation approaches based on internal markers was proposed by Schweikard et al. [12], who combined real-time tracking of skin markers with occasional detection of implanted internal markers based on X-ray imaging for motion compensation during radiosurgery. Another related study was performed by Zhang et al. [13], in which one electromagnetically tracked fiducial needle was used in addition to skin markers to improve registration precision during percutaneous liver punctures. However, the skin markers were not tracked and the authors did not evaluate the TRE for different numbers of skin markers and fiducial needles. Moreover, only rigid registration was performed, and the tracking data were not fed into a (non-rigid) deformation model to compensate for liver motion in real time. A study closely resembling ours has recently been published by Krücker et al. [14], who performed experiments in a swine model to investigate registration and motion correction methods in the presence of respiratory motion. The authors applied either a set of skin markers or a set of fiducial needles for this purpose. Similar to us, they concluded that respiratory motion can be compensated for throughout the respiratory cycle when using internal fiducials. Even though this work was similar to our own, there are some major differences. First, the authors did not investigate combining internal and external markers for continuous motion compensation. Second, they only tracked the tips of the fiducial needles and did not feed additional points from the axes of the tools into the deformation model. Hence, they effectively used 3-degree-of-freedom (3-DoF) tools, as opposed to 5-DoF or 6-DoF tools. Third, an electromagnetic tracking system was employed, which (according to the authors themselves) may have led to inaccurate tracking data due to interference with the CT scanner. Finally, the reference target needle position was potentially inaccurate because the tools were not anchored within the tissue. Hence, the two studies, while overlapping in part, can be regarded as complementary.

To our knowledge, we are the first to combine internal and external markers to compensate for organ motion in real time. Based on the results of this study, we suggest using one fiducial needle and (at least) two skin markers, as well as applying an affine deformation model for motion compensation during CT-guided liver punctures.

Several issues remain to be addressed. In this study, we concentrated on the accuracy of the deformation model by assuming an ideal initial registration of the tracking coordinate system with the CT coordinate system. Future work should evaluate the calibration accuracy of the navigation tools and of locating them in the CT image (fiducial localization error (FLE)). In a previous study [11], we performed an experimental investigation in a respiratory motion simulator of suitable placement strategies for two fiducial needles. This work could be extended from a theoretical point of view by estimating the TRE for different fiducial arrangements based on the distribution of the FLE (see references [15] and [16]). Our study suggests that monitoring of FRE_rigid could be used for performing gated interventions. It remains to be shown, however, that continuous monitoring of FRE_rigid can be used to support an intervention in practice. When extracting a binary gating curve from the tracking data based on FRE_rigid, a Kalman filter could be applied to prevent outliers from making the interventional phases too short. Still, even visualization of FRE_rigid by itself during an intervention could be helpful. If deep inhalation yields a higher FRE_rigid than flat inhalation, for example, the patient can be asked to adjust the breathing pattern accordingly. It is worth noting that our proposed motion compensation approach could also be applied in radiotherapy treatment. In this case, the tracking data would have to be fed into a prediction model to take into account system latency.

In conclusion, the results of this study could be used in practice to decide on a suitable combination of fiducials for a given intervention, considering the trade-off between high accuracy and low invasiveness, and to provide an intra-interventional measure of confidence in the accuracy of the system based on the FRE of a rigid transformation reflecting tissue motion.

Acknowledgements

The present study was conducted within the context of “Research Training Group 1126: Intelligent Surgery - Development of new computer-based methods for the future workplace in surgery”, funded by the German Research Foundation (DFG).