A computer aided method for closed reduction of diaphyseal tibial fracture using projection images: A feasibility study

Abstract

A computer aided method for closed tibial shaft fracture reduction based on measurements of 12 projection parameters (6 angulations and 6 translations) from an anteroposterior radiograph, a lateral radiograph, and a transverse projection photograph is examined. The development, validation and reliability of the computer aided method are presented. A custom-made unilateral external fixation device consisting of 7 calibrated one-degree-of-freedom joints was employed to execute the reduction. Five tibial fracture phantoms with initial deformities that covered a wide range of misalignments were tested. The mean (standard deviation) resultant rotational and translational errors after the reduction were 3.32° (0.96°) and 1.65 (0.86) mm, respectively, which indicates good reduction accuracy. Three independent raters made the measurements of the projection parameters to test inter-rater reliability. The intra-class correlation coefficients were found to range between 0.935 and 1, indicating good reliability. Since ideal patient positioning for AP, lateral and transverse image acquisition is not easily attainable, the effect of patient positioning errors on the measurement of projection parameters was explored using a tibial phantom. The preliminary results revealed that 10° deviations in positioning do not greatly affect the measurement of AP and lateral angulation parameters (<1.7°). However, a 10° positioning error about the long bone axis may result in a change of as much as 10.7° in the measurements of transverse projection angulation parameters. In addition, a 10° positioning error about an arbitrary anatomical axis may result in translational projection parameter changes of up to 6.8 mm. For these reasons, a previously validated method that allows for accurate positioning of the tibia about its long axis and a two-step reduction strategy to achieve the best possible deformity reduction are proposed. Procedures to facilitate reliable measurement of tibial torsion are also discussed. It appears that the projection-based reduction method exposes the patient to less radiation and allows for simple, quick and accurate reductions, making it an attractive choice for acute clinical applications.

• Closed reduction
• tibial shaft fracture
• external fixation
• computer aided surgery

Introduction

The tibia is the most commonly fractured long bone in the body. Alho et al. reported an annual incidence of two diaphyseal tibial fractures per 1000 individuals [1]. Diaphyseal tibial fractures commonly occur after falls, car accidents and sports injuries. They can be treated by several methods, including casting, intramedullary nailing, screws and plates, and external fixation, depending on the type of fracture and alignment of the tibia. External fixation is commonly used to treat displaced diaphyseal tibial fractures, especially those involving severe soft-tissue injuries and open wounds [2]. Prior to external fixation, closed reduction must be done to realign the fracture fragments. Accurate anatomical reduction has been shown to have beneficial effects in reducing the time to union [3],[4], lowering the likelihood of malunion and nonunion [5], and improving the function and appearance of the limb [6].

The conventional approach to closed reduction using an external fixator is a subjective and time-consuming process. It involves repeated unlocking of the fixator joints, manipulation of the fracture site, re-locking of the fixator joints, and viewing of the alignment based on static two-dimensional (2D) fluoroscopic images. It is challenging to reduce a three-dimensional (3D) deformity based on the limited field of view and static 2D fluoroscopic images. The complexity of this process often results in the surgeon making a compromise between the quality of reduction and the time taken. This approach may also cause excessive tissue disruption around the fracture site, comprising tissue integrity. In addition, both the surgeon and patient are exposed to a substantial amount of radiation [7].

To improve the reduction accuracy, computer assisted navigation techniques have been employed in closed fracture reduction. Hofstetter et al. [8],[9] and Weil et al. [10],[11] used fluoroscopy-based navigation techniques, in which the bone fragments are displayed through superimposed line graphics on multiplanar intraoperative fluoroscopic images to provide the real-time spatial relationship between the bone fragments in a pseudo-3D manner. Several groups [12–14] have developed CT-based navigation systems, for which the bone fragments are segmented and reconstructed in three dimensions from the preoperative CT images, registered with the intraoperative data, and tracked intraoperatively using an optical kinematic tracking system. Although these navigation techniques provide pseudo-3D or 3D images to aid the reduction process, the surgeon must still manipulate the fracture site indirectly by viewing the visual cues from the computer monitor. Significant skill is still required to control precisely the spatiotemporal relationship between the fracture fragments and to maintain eye-hand coordination while performing the adjustments.

Various specially designed fracture-reduction devices have also been developed to improve the reduction process [15–19]. These devices allow the reduction maneuvers at each degree of freedom to be implemented independently of one another, and hence give the surgeon greater control during the reduction process. However, they do not provide a knowledge-based technique that calculates the adjustment requirements of the apparatus being used to reduce a fracture deformity; the surgeon must still rely on subjective judgment to adjust each control component.

Knowledge-based fracture reduction using special ring-type external fixators [i.e., the Taylor Spatial Frame (Smith & Nephew, Memphis, TN) and Hexapod Ilizarov fixator (LITOS GmbH & COKG, Hamburg, Germany)] has been reported in the literature [20–23]. The fixator systems are similar, each consisting of two rings connected by 6 telescopic struts at special universal joints. By adjusting the strut lengths according to the adjustment requirements calculated by a computer program, one fracture fragment can be positioned with respect to the other. This approach is attractive because it makes the reduction process more objective and experience-independent; however, the success of the reduction depends very much on the measurement accuracy of the input parameters. For instance, the Taylor Spatial Frame requires a surgeon to measure 13 parameters preoperatively, including six deformity parameters, three frame parameters and four mounting parameters. Errors in any one parameter propagate through the entire preoperative plan. Of the input parameters, axial rotational deformity is especially prone to error because it is only determined by clinical examination [21],[22]. Errors associated with limb positioning during X-ray projections may also affect the accuracy of the other five deformity parameters. Nonetheless, these issues have not been addressed in the literature.

A unilateral external fixator, namely the Bone Reposition Device (BRD), was recently developed [24] to facilitate the implementation of a CT-based reduction method [25]. Although the CT-based method allows a surgeon to perform fracture reduction in an objective and accurate manner, the high cost, limited availability, patient transport concerns, and other logistical requirements make CT less feasible in small clinical settings. These practical constraints ground the premise of the current study. This paper presents a projection-based method that uses the BRD to perform knowledge-based reduction of diaphyseal tibial fractures. Of special interest is the testing of the validity of the projection-based reduction algorithm, exploring the impact of limb positioning errors on input parameters, and evaluating inter-rater reliability in the measurement of input parameters. Part of this research has previously been reported in abstract form [26].

Methods

Theoretical consideration

The Bone Reposition Device (BRD) is a unilateral external fixation device which features seven one-degree-of-freedom joints, each allowing for continuous adjustment, and is equipped with measurement components to facilitate accurate positioning (see reference [24] and Figure 1). With the BRD attached to a tibia with a displaced diaphyseal fracture, the bone-device complex can be regarded as an open kinematic chain allowing rotation and translation at the fracture site through adjustment of the BRD joints. By defining a local coordinate system on each device component, pin clamp and fracture fragment, the spatial relationship between the proximal and distal fracture fragments before [Equation (1)] and after [Equation (2)] the reduction can be expressed as products of transformation matrices: where A and B represent “after” and “before” reduction, respectively, D and P represent the distal and proximal fracture fragment, 1 and 8 represent the distal and proximal pin clamp, and 2–7 represent the six device components from distal to proximal. Each item within the equations is a 4 × 4 homogenous transformation matrix, which describes the spatial relationship of the subscript local coordinate system to the superscript local coordinate system [27]. Given that the elements within are functions of the positions of the BRD joints, the configuration of the BRD that reduces a fracture deformity can be computed, provided that [^DT_p]_A,[⁸T_p]_Aand[^DT₁]_A can be accurately estimated preoperatively.

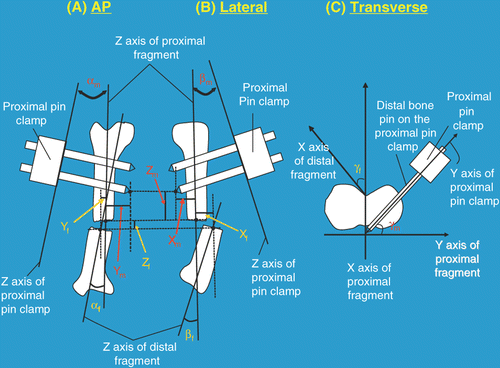
Figure 1. Definitions of the twelve projection parameters. Six parameters (i.e., 3 translations and 3 angulations) are required to quantify the fracture deformity and a further six parameters (i.e., 3 translations and 3 angulations) are required to quantify the spatial relationship between the proximal pin clamp and the proximal fracture fragment. (1) Angulation parameters: Lines are drawn along the longitudinal axes of the proximal and distal fracture fragments on both the AP (A) and lateral (B) X-ray images. The angles between them are the AP view fracture site angulation (α_f) and the lateral view fracture site angulation (β_f), respectively. Lines are also drawn along the longitudinal edge of the proximal pin clamp on the AP and lateral X-ray images. The angles between the pin clamp line and the proximal fracture fragment line on the AP and lateral view are the AP view mounting angulation (α_m) and lateral view mounting angulation (β_m), respectively. On the transverse projection photograph (C), the angle between the AP axes of the distal and proximal fracture fragments is the transverse view fracture site angulation (γ_f). The angle between a line along the distal bone pin of the proximal pin clamp and the lateral axis of the proximal fracture fragment is the rotational mounting offset (γ_m). With the frontal plane of the proximal tibial fragment positioned parallel to an examination table, the AP and lateral axes of the proximal fracture fragment correspond to vertical and horizontal lines on the transverse photograph. (2) Translation parameters: On both the AP (A) and lateral (B) X-ray images, the origins of each fracture fragment are defined as the centroid of the outline of each fracture end. The three components of fracture site translations (x_f, y_f, z_f) correspond to the x, y, z components of a vector from the origin of the proximal fracture fragment to the origin of the distal fracture fragment in terms of the local coordinate system of the proximal fracture fragment. The origin of the proximal pin clamp is defined as the tip of the distal bone pin of the proximal pin clamp. Hence, the three components of mounting translations (x_m, y_m, z_m) are the x, y, z components of a vector from the origin of the proximal fracture fragment to the origin of the proximal pin clamp in terms of the local coordinate system of the proximal fracture fragment. z_f and z_m can be measured in both the AP and lateral view.

Matrix estimation

Prior to the reduction, the BRD is attached to the anteromedial side of the fracture fragments in an arbitrary configuration to temporarily stabilize the fracture site. Twenty parameters are measured preoperatively, including 7 device configuration parameters, 7 mounting parameters and 6 deformity parameters. The device configuration parameters represent the joint positions of the BRD before the reduction. They can be read directly from the measurement components of the BRD's joints, which define transformation matrices [¹T₂]_B, [²T₃]_B, [³T₄]_B, [⁴T₅]_B, [⁵T₆]_B, [⁶T₇]_B and [⁷T₈]_B in Equation (1). Two radiographs are acquired such that the X-ray film plates are aligned with the frontal and sagittal planes of the proximal tibial fragments, respectively. Five deformity parameters [i.e., the AP and lateral view fracture site angulations (α_f, β_f) and the three components of the fracture site translations (x_f, y_f, z_f)] and five mounting parameters [i.e., the AP and lateral view mounting angulations (α_m, β_m) and the three components of the mounting translations (x_m, y_m, z_m)] are measured from the radiographs using ImageJ 1.36b (National Institutes of Health, Bethesda, MD) in accordance with Figure 1A and B. With the frontal plane of the proximal tibial fragment positioned parallel to an examination table, a digital photo is also taken perpendicular to the transverse plane of the proximal tibial fragment. Projection angles between the X axes of the distal and proximal fracture fragments [i.e., the transverse view fracture site angulation (γ_f)] and between the Y axes of the proximal pin clamp and the proximal fracture fragment [i.e., the rotational mounting offset (γ_m)] are measured from the photo in accordance with Figure 1C. The pin offset distance is the last mounting parameter and is measured directly with a caliper as the distance between the blunt end of the distal bone pin of the proximal pin clamp and the side surface of the proximal pin clamp (Figure 1A).

With these mounting and deformity parameters, [⁸T_P]_B and [^DT_P]_B can be determined according to the formulation described in the Appendix. Hence, one can solve Equation (1) to get [^DT₁]_B. Since each pin clamp can be regarded as being rigidly connected to its respective fracture fragment via a pair of bone pins, the spatial relationship between fracture fragment and pin clamp will be the same before and after reduction (i.e., [⁸T_P]_B = [⁸T_P]_A and [^DT₁]_B = [^DT₁]_A). By definition, the local coordinate systems of the proximal and distal fracture fragment are assumed to overlap with one another after the reduction (i.e., [^DT_P]_A is an identity matrix). Hence, Equation (2) can be solved for the final joint positions that reduce the fracture deformity using non-linear least square optimization [24].

Use of the BRD as a reduction template

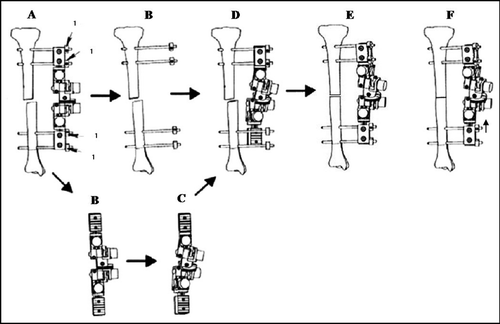
Once the joint adjustment requirements are determined, four pin offset locators are attached next to the side surface of the proximal and distal pin clamps (Figure 2A). The BRD is then detached, leaving the bone pins still secured to the fracture fragments (Figure 2B). Next, the BRD is adjusted and locked off-site according to the calculated adjustment requirements, except that additional translation of, say, 10 mm, can be applied to the proximal/distal telescopic joint (Figure 2C). Once adjusted, the proximal pin clamp of the BRD is re-attached to the proximal bone pins with the side surface aligned with the respective pin offset locators (Figure 2D). Hence, the distal pin clamp can now serve as a template to guide the surgeon in manipulating the distal fracture fragment until the distal bone pins are positioned back at the distal pin clamp at the original pin offset distance (Figure 2E). Finally, the proximal/distal telescopic joint is adjusted to close the fracture gap and complete the reduction (Figure 2F).

Figure 2. Workflow for using the Bone Reposition Device (BRD) as a template to guide the reduction process (1 = pin offset locator).

Validation of the Algorithm

A laboratory experiment was conducted on 5 tibia phantoms (Sawbones, Pacific Research Laboratories, Inc., Vashon, WA) to test the validity of our projection-based reduction algorithm. A fracture deformity was arbitrarily introduced to each phantom so that together they covered a wide range of misalignments (Table I). Two Acrylite® rectangular blocks with faces parallel to the anatomical planes were attached to the proximal and distal ends of the tibia phantoms (Figure 3C). The proximal block facilitated accurate positioning of the tibia phantoms for image acquisition, whereas the distal block facilitated the measurement of transverse view fracture site angulation. AP and lateral radiographs as well as a transverse projection photo were acquired for each fracture model (Figure 3) and the deformity and mounting parameters were measured. These parameters, along with the initial configuration parameters, were used as input into the projection-based reduction algorithm to calculate the adjustment requirements. The BRD was then adjusted off-site and acted as a template to guide the reduction.

Figure 3. Anteroposterior (AP) X-ray (A), lateral X-ray (B) and transverse photo images (C) of a tibia phantom used in the laboratory validation. Lines and origins were superimposed and six deformity and six mounting parameters were then measured from the images. Pin offset distance and 7 joint configuration parameters were also measured preoperatively.

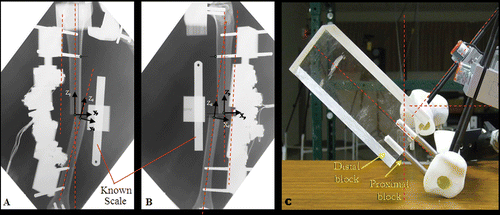
Table I.  Initial deformities of the five displaced tibial fracture models.

				Euler angles (°)				Translations (mm)
Phantom	Side^1	Fracture type^2	θ (°)	1	2	3	d (mm)	x	y	z
A	L	T	22.76	−13.29	13.11	14.73	29.28	−23.51	14.74	−9.33
B	L	T	12.08	6.78	−3.90	−8.99	42.39	33.93	22.34	12.11
C	L	O	17.14	2.49	−9.51	14.27	36.45	−36.39	−2.10	−0.70
D	R	T	47.98	−4.67	9.30	−46.52	41.96	−19.66	30.09	21.66
E	R	O	32.85	8.48	19.11	−26.96	36.24	−28.12	1.00	22.84

¹L: Left; R: Right. ²T: Transverse fracture; O: Oblique fracture. θ represents the resultant rotation before reduction. d represents the distance between the origins of the proximal and distal local coordinate systems before reduction. The Euler angles and translation components are expressed in terms of the anatomical coordinate system.

The reduction accuracy was quantified by an anatomical-based method [24]. In brief, the method defines a local coordinate system on each fracture fragment which corresponds to the anatomical coordinate system of an intact tibia. These local coordinate systems overlap with one another if the fracture fragments are perfectly aligned. Therefore, any discrepancies between these local coordinate systems can be regarded as reduction errors. Three translation error components (x_e, y_e, z_e), representing the x, y and z coordinates of the origin of the distal fragment with respect to the local coordinate system of the proximal fragment, and three rotational error components, representing the Euler angles θ₁, θ₂ and θ₃ based on the X-Y-Z rotational sequence [28], were calculated and used to quantify the rotational and translational errors of the projection-based reduction method. The resultant rotational (θ_r) and translational errors (d_r) were also computed.

Inter-rater reliability analysis of projection parameters

Due to uncertainty in defining the projection axes and boundaries of the fracture ends, the measurement of projection parameters may vary between raters. This will in turn affect the joint configuration calculated by the algorithm. The inter-rater reliability of the measurement of projection parameters was evaluated. Three raters measured the projection parameters from the radiographic images of five tibia phantoms independently using ImageJ. Each was blinded to the measurement results from the others. One rater had extensive anatomical background, while the other two had a basic anatomical understanding. Before making the measurements, a training session was provided to each rater. A user manual was also provided to each rater throughout the analysis to ensure consistency of the measurement protocol among the raters. Intra-class correlation coefficient (ICC) models were applied to study the degree of correspondence and agreement among the raters. ICC(3,1) was calculated for all projection parameters on the radiographic images except z_f and z_m, which were quantified using ICC(3, 2) because these two parameters could be measured in both the AP and lateral X-ray images. The F ratios associated with the rater effect were used to test the extent of agreement among the raters [29].

Effects of limb positioning on projection parameters

A preliminary study was conducted using a tibia phantom (Model D) to explore the influence of limb positioning on the deformity and mounting parameters. AP and lateral projection parameters (i.e., α_f, β_f, α_m, β_m, x_f, y_f, z_f, x_m, y_m, z_m) were measured with the tibia positioned at ±10° rotation about the y and z axes and the x and z axes, respectively. The transverse view fracture site angulation (γ_f) and rotational mounting offset (γ_m) were measured at ±10° rotation about the x, y and z axes, respectively. These rotations were achieved by placing a 10° wedge under the proximal block along the corresponding direction. Rotation about the x axis was not evaluated for the AP projection because it has no effect on the AP projection parameters since the rotation is in the same plane. Similarly, rotation about the y axis was not evaluated for the lateral projection. Translation between fragments is measured from an origin on the proximal fragment to an origin on the distal fragment. The choice of origins is wide open as long as they are coincident in the reduced state. In this study, a pair of radiopaque fiducial markers were embedded at the tip of the proximal and distal fragments in such a way that they were coincident in the reduced state. This defined a control origin pair, which allowed study of the effects of limb positioning on translation parameters. A second origin pair was defined as the centroids of hand-drawn outlines about the end of each fracture fragment computed by ImageJ. The third origin pair was defined as the center point of each fracture end based on the best guess of the rater. Changes in projection parameters were evaluated as the mean absolute difference between the parameter as measured in the true frontal, sagittal and transverse planes and the same parameter as measured in a plane with introduced error to explore the effects of limb positioning.

Results

The reduction error of the projection-based method implemented using the BRD is summarized in Table II. The mean values of each translational (i.e., x_e, y_e and z_e) and rotational (i.e., θ₁, θ₂, θ₃) error component were 0.80 (SD = 0.70), 1.07 (SD = 1.04) and 0.33 (SD = 0.42) mm, and 1.99° (SD = 4.47°), 1.69° (SD = 0.69°) and 1.23° (SD = 1.30°), respectively. The mean resultant rotational (θ_r) and translational (d_r) errors were 3.32° (SD = 0.96°) and 1.65 (SD = 0.86) mm, respectively. These results demonstrated the validity of the projection-based reduction algorithm. The pre- and post-reduction of one of the phantoms is shown in Figure 4 as an example to illustrate the reduction accuracy.

Figure 4. Bone alignment before and after projection-based fracture reduction of model A. Left: Before reduction (θ_r = 22.76°, d_r = 29.28 mm); Right: After reduction (θ_r = 3.07°, d_r = 1.41 mm).

The ICCs of the ten projection parameters were found to range between 0.935 and 1 (Table III), which indicates good reliability. The F ratios also revealed that the rater effect on the projection parameter measurements was not significant (P > 0.05 for all parameters; see Table III).

Table II.  Reduction accuracy for the five tibia phantoms.

				Euler angles (°)				Translations (mm)
Phantom	Side^1	Fracture type^2	θr (°)	θ1	θ2	θ3	dr (mm)	xe	ye	ze
A	L	T	3.07	−0.102	−2.799	−1.265	1.41	0.965	−0.865	−0.553
B	L	T	2.30	0.860	−1.732	1.251	0.80	−0.099	0.790	−0.095
C	L	O	2.63	2.466	−0.909	0.023	3.04	0.098	−2.884	0.972
D	R	T	3.95	−3.634	−1.523	0.293	1.80	1.705	0.580	0.019
E	R	O	4.64	−2.910	−1.465	−3.335	1.17	1.142	0.248	0.012

¹L: Left; R: Right. ²T: Transverse fracture; O: Oblique fracture. θ_r represents the resultant rotation after reduction. d_r represents the distance between the origins of the proximal and distal local coordinate systems after reduction. The Euler angles and translation components are expressed in terms of the anatomical coordinate system.

Table III.  Inter-rater reliability of the projection parameters on the X-ray images.

Parameters	ICC (3,1)	F ratio	P
AP-view fracture site angulation (αf)	0.996	0.477	0.637
AP-view mounting angulation (αm)	0.977	2.404	0.152
Lateral-view fracture site angulation (βf)	0.991	0.879	0.452
Lateral-view mounting angulation (βm)	0.973	0.410	0.677
Fracture site translation (yf)	0.999	0.959	0.423
Mounting translation (ym)	0.935	0.437	0.660
Fracture site translation (xf)	0.997	2.444	0.148
Mounting translation (xm)	0.965	1.256	0.335
*Average fracture site translation (zf)	1	2.247	0.168
*Average mounting translation (zm)	1	1.862	0.217

*Given that z_f and z_m can be measured from both AP and lateral X-ray projections, the average of the two measurements was used for the analysis. Hence, ICC (3, 2) was used instead.

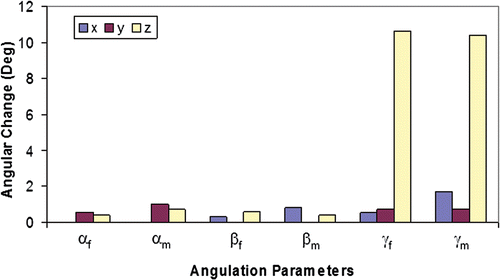
The effects of limb positioning on the fracture site and mounting angulation parameters are summarized in Figure 5. The 10° positioning error about the z axis in the transverse view resulted in changes of 10.41° and 10.64° in the rotational mounting offset (γ_m) and transverse view fracture site angulation (γ_f), respectively. However, a 10° positioning error about the other axes did not substantially change the other angulation parameters (i.e., α_m, α_f, β_m, β_f). Differences with respect to those parameters measured at true projection ranged from 0.33 to 1.69°.

Figure 5. Effects of limb positioning errors on angulation parameters: Measured changes in angulation parameters (α_f, α_m, β_f, β_m, γ_f, γ_m). Changes are expressed as the mean absolute difference between the parameter as measured in the true frontal, sagittal and transverse planes and the same parameter as measured in a plane with introduced error of ±10° about the axis indicated.

Changes in fracture site and mounting translation parameters resulting from a 10° positioning error about each axis are shown in Figure 6. Average values of 3.20 (SD = 1.55) and 1.16 (SD = 0.64) mm; 3.33 (SD = 2.01) and 1.67 (SD = 0.94) mm; and 3.21 (SD = 2.07) and 1.58 (SD = 0.91) mm were found for the “Fiducial”, “Centroid” and “Best Guess” methods, respectively.

Figure 6. Effects of limb positioning errors on translation parameters: Measured changes in translation parameters (X_f, Y_f, Z_f, X_m, Y_m, Z_m). Changes are expressed as the mean absolute difference between the parameter as measured in the true frontal, sagittal and transverse planes and the same parameter as measured in a plane with introduced error (x, y, z indicate the axis about which ±10° was introduced). The parameters resulting from three methods of identifying the fragment origins (Best Guess, Centroid, and Fiducial) are compared.

Discussion

By measuring 6 deformity, 7 mounting, and 7 joint configuration parameters of the BRD, we were able to calculate the final configuration of the BRD that reduced a fracture deformity. The time required for parameter measurements and solution calculation was estimated to be less than 20 minutes. We have shown with laboratory experiments that the algorithm used in the projection-based reduction method results in good reduction accuracy, as evidenced by the small residual reduction errors. The method also has a high degree of reliability, as evidenced by the calculated ICC and F values.

In this study, we modified the tibia phantoms by using the proximal block to clearly define the anatomical coordinate system for the purpose of validating our algorithm. In doing so, we eliminated the uncertainty in producing true AP, lateral and transverse projection images. In a clinical situation, ideal patient positioning for AP, lateral and transverse image acquisition is not easily attainable. It has been found that patient positioning errors can affect the measurement of a variety of parameters commonly collected from 2D radiographic data, including bone density, bone deformity, and alignment angles [30–33]. Therefore, the introduction of systematic positioning errors allowed us to assess the effect of such errors on projection parameters. Our preliminary results revealed that small deviations in positioning do not greatly affect the measurement of AP and lateral angulation parameters (α_m, α_f, β_m, β_f). However, positioning error about the z axis has a direct effect on measurement of transverse projection angulation parameters (γ_f, γ_m) due to the fact that γ_f and γ_m are defined with respect to the vertical and horizontal line on the transverse projection image, respectively. Errors in the measurements of γ_f and γ_m would result in rotational malunion, which is a major cause of morbidity following tibial fracture fixation. Consequently, in a clinical situation, it is important to accurately position the tibia about the z axis. It has been reported that accurate positioning of the proximal tibia parallel to its AP anatomical plane can be achieved precisely with as little as 1° offset using a fluoroscopic method [34] (described in detail below).

In a majority of cases in current clinical practice, evaluation of rotational deformity is performed without the aid of an instrument and the degree of tibial torsion is estimated on the basis of clinical examination [35]. It has been shown that a large percentage of these estimated torsion angles exceed an acceptable limit and are missed upon clinical examination [35]. To improve the measurement accuracy for rotational deformity in a clinical setting, we propose to use the contralateral side as a reference and determine the rotational deformity of the fractured tibia as follows:

The subject is placed supine on an examination table with the knee joint of the intact leg fully extended. This makes axial rotation of the knee joint impossible (i.e., the tibia and femur can be regarded as a functional unit). The long bone axis of the intact tibia is first positioned parallel to the examination table. The foot is firmly supported in the neutral position against a vertical Plexiglas support at the end of the table. Under fluoroscopic control, the leg is rotated in such a way that the posterior contours of both femoral condyles are superimposed on one another in the horizontal plane [34],[36–39]. With the leg rested in the aligned position, the table surface is defined as the frontal plane of the tibia. On the Plexiglas support, a reference line is drawn from the center of the heel toward the interspace between the first and second toes. The angle between this line and a line perpendicular to the examination table is denoted as θ. A line inclined by θ with respect to the reference line is drawn on the sole of the fracture side. The positioning procedure is then repeated for the fracture side. A digital camera is mounted perpendicular to the Plexiglas support, which captures a projection image of the foot on the transverse plane of the proximal tibia. The projection angle between the line marked on the sole (i.e., the AP axis of the distal fragment) and a vertical line on the Plexiglas support (i.e., the AP axis of the proximal fragment) is denoted as the transverse view fracture site angulation (γ_f). It is believed that this procedure will substantially reduce the potential errors resulting from positioning errors of the tibia about the z axis, and make the measurement of transverse projection angulation parameters more accurate.

In this study, we used fiducial markers to create well defined and easily measured points representing the origins of each fracture fragment. Although this method is difficult to implement in actual clinical practice, it reflects the induced translational projection parameter changes associated with positioning error alone. Increased changes and larger variance in translation input parameters introduced by the “Centroid” and “Best Guess” methods are seen when compared with the “Fiducial” method. These increases may be attributed to human error either in defining the “best guess” origins or in outlining the fracture fragment ends. We have shown that, while there are inherent errors associated with estimating the origins in planar views of a 3D deformity, these errors do not result in huge changes in the translational input parameters. Neither the “Best Guess” nor “Centroid” methods appear to be superior in defining coincident origins. We believe that consistency among raters will be improved by using the “Centroid” method, since it is better delineated and less subjective. It appears that both the means and standard deviations of changes in the fracture site translation parameters are larger than those for the mounting translation parameters. At each orientation, the weight of the BRD may cause the bone pins to bend slightly in a different direction, which would affect the measurement of fracture site translational input parameters.

Malunion is generally defined as a fracture that has healed with an angular deformity of greater than 5° in any anatomical plane or a translational deformity greater than 10 mm [40]. Our laboratory results demonstrate the ability of the projection-based method to successfully prevent malunion immediately after reduction for all five tibial phantoms (Table II). However, we have also shown that a 10° positioning error about an arbitrary anatomical axis results in translational changes as large as 6.8, 4.9, 5.1, 3.6, 2.2 and 2.0 mm for x_f, y_f, z_f, x_m, y_m and z_m, respectively (Figure 6). Hence, it is possible that, after the primary reduction, a significant amount of residual translation may still exist. For this reason, calculation of a secondary reduction configuration may be necessary to achieve the best possible reduction. Given that the angular deformity should have been adequately reduced after the primary reduction, measurement of translational input parameters for the secondary reduction will be less sensitive to positioning errors. With this proposed additional methodology we would expect exceptionally accurate and reproducible fracture reduction outcomes.

Unlike the CT-based method developed for use with the BRD, which uses a 3D reconstruction of the fracture fragments and calculates the reduction based purely on the bone's geometry [24], the 12 projection parameters used in the reduction algorithm in this study are specific to the tibia. It is plausible that a similar set of parameters could be developed and used to reduce fractures in other bones. However, the reduction of rotation about the long axis of the bone may prove particularly difficult in some instances. If we assume bilateral symmetry, then using the transverse photograph we can approximate the amount of rotation needed to match the rotation seen in the unaffected limb. A similar image needed to evaluate the rotation about the long axis is not apparent for each bone that may need to be re-aligned.

There are a few potential sources of error that may affect definition of the local coordinate system on both the proximal and distal fracture fragments. The long bone axis of the proximal fragment defines the direction of the y and z (x and z) axes in the AP (lateral) projection. Therefore, variation in defining the long bone axis not only affects the AP and lateral view angulation parameters, but also the translation parameters. The assumption made in the alignment algorithm implies that when the two fracture fragments are perfectly aligned the two local coordinate systems are also perfectly aligned and overlapping and can therefore be represented in the algorithm as an identity matrix. Improper definition of either fracture fragment local coordinate system will affect the validity of this assumption. The assumption of an identity matrix in this case implies that each anatomically defined axis can be approximated faithfully from the parameters measured. Proper definition and measurement of each parameter is crucial to the accuracy of the method, and we have shown here (via intra- and inter-reader reliability assessments) that consistent measurements can be made, but that errors in patient positioning may also have small effects on the measurement of projection parameters.

To the authors’ knowledge, the Taylor Spatial Frame and Hexapod Ilizarov fixator are the only commercially available systems that incorporate a computational algorithm to correct fracture deformity [20–23]. The concept of our projection-based method resembles the total residual deformity correction method of the Taylor Spatial Frame, except that a unilateral external fixation device is used to execute the reduction. However, there is no quantitative data available in the literature regarding the accuracy and reliability of reduction with these systems. We therefore plan to conduct a comparative study to evaluate their ease of use, accuracy and reliability.

In summary, the projection-based method reported here allows surgeons to perform closed fracture reduction in an objective, efficient and accurate manner. It also reduces radiation exposure for both the surgeon and the patient. With the BRD acting as a targeted guide, the surgeon can concentrate on manipulating the fracture fragments to facilitate a smooth transition from the displaced, initial position to the reduced, final position. Theoretically, this will be a less experience-dependent means of executing the reduction, and will lessen the extent of periosteum and soft tissue disruption around the fracture site. It therefore appears that the projection-based reduction method is an attractive choice for acute clinical applications.

Acknowledgments

The authors would like to thank Dr. John A.M. Taylor for the use of X-ray equipment and his fruitful advice on X-ray imaging, Dr. Mathew Richardson for his technical support in taking the X-ray images, Dr. Arthur F.T. Mak for providing the Bone Reposition Device, Dr. Jeanmarie Burke for her general support of the project, and Mr. Cory Bingham, Ms. Stefanie Coforio, Ms. Artella Oh, Mr. Matthew Dimond and Mr. Erik Uuksulainen for their assistance in conducting the validation experiment. This study was supported by Foot Levelers, Inc.

Appendix: Determination of and []_B

(1) Determination of from deformity parameters

Based on the x, y’, z’’ rotation sequence about the instantaneous axes of {D}, the 4 × 4 transformation matrix [^DT_P]_B can be expressed as follows: where is a rotation matrix and is the position vector that locates {P}'s origin with respect to {D} at the state of “before” reduction; c and s represent cosine and sine; and 1, 2 and 3 represent the three Euler angles.

Each component of can also be written as the dot product of a pair of unit vectors: where x_P, y_P, z_P and x_D, y_D, z_D are the unit vectors of the proximal and distal fracture fragments, respectively.

Euler angle 1

Based on the AP projection (i.e., the projection on the yz plane of the proximal fragment), the unit vectors (x_D, y_D, z_D) of the distal fragment can be determined from the projection only within an unknown scale coefficient (respectively, fr_x, fr_y, fr_z) [41]. These vectors have the following coordinates, obtained from Equation (4): where ify stands for the y coordinate of the frontal projection of the x_D unit vector.

From (5), where α_f is the AP view fracture site angulation (i.e., the angle between the z_P and z_D projected on the yz plane of the proximal fracture fragment).

Euler angle 2

Based on the lateral projection (i.e., the projection on the xz plane of the proximal fragment), the unit vectors (x_D, y_D, z_D) of the distal fragment can be determined from the projection only within an unknown scale coefficient (respectively, sa_x, sa_y, sa_z) [41]. These vectors have the following coordinates, obtained from Equation (4): where isx stands for the x coordinate of the sagittal projection of the x_D unit vector.

From (7), where β_f is the lateral-view fracture site angulation (i.e., the angle between the z_P and z_D projected on the xz plane of the proximal fracture fragment).

Euler angle 3

Applying the decomposition procedure as described above to the transverse projection (i.e., the projection on the xy plane of the proximal fragment), Euler angle 3 can be expressed as follows: where γ_f is the transverse view fracture site angulation (i.e., the projected angle between the x_P and x_D projected on the xy plane of the proximal fracture fragment).

Translation parameters [(x), (y), (z)]

Fracture site translation components [y_f, z_f] can be determined from the AP X-ray projection after the magnification factor of the AP radiograph is taken into account. Similarly, fracture site translation components [x_f, z_f] can also be determined from the lateral X-ray projection. These magnification factors were estimated by placing a known metal scale parallel to the projection plane and at a latitude similar to that of the tibia phantom. The position vector can then be calculated by the following relationship: where

This concludes the demonstration of how [^DT_P]_B can be determined from AP, lateral and transverse projections.

(2) Determination of [⁸T_P]_B from mounting parameters

Similarly to (4), rotation matrix can be expressed as follows: where x_P, y_P, z_P and x₈, y₈, z₈ are the unit vectors of the proximal fracture fragment and the proximal pin clamp, respectively.

Euler angles 1 and 2, as well as the three translation parameters of , can be determined by substituting the deformity parameters with the mounting parameters. i.e., where α_m is the AP view mounting angulation. where β_m is the lateral view mounting angulation. where = [x_m, y_m, z_m]^T and x_m, y_m, z_m are the mounting translations.

Applying the similar decomposition procedure as described above to the transverse projection (i.e., the projection on the xy plane of the proximal fragment), Euler angle 3 can be expressed as follows: where γ_m is the rotational mounting offset (i.e., the projected angle between the y_P and y₈ projected on the xy plane of the proximal fracture fragment).

This concludes the determination of [⁸T_P]_B.