Error analysis for determination of accuracy of an ultrasound navigation system for head and neck surgery

Abstract

Objective: The use of conventional CT- or MRI-based navigation systems for head and neck surgery is unsatisfactory due to tissue shift. Moreover, changes occurring during surgical procedures cannot be visualized. To overcome these drawbacks, we developed a novel ultrasound-guided navigation system for head and neck surgery. A comprehensive error analysis was undertaken to determine the accuracy of this new system.

Materials and Methods: The evaluation of the system accuracy was essentially based on the method of error definition for well-established fiducial marker registration methods (point-pair matching) as used in, for example, CT- or MRI-based navigation. This method was modified in accordance with the specific requirements of ultrasound-guided navigation. The Fiducial Localization Error (FLE), Fiducial Registration Error (FRE) and Target Registration Error (TRE) were determined.

Results: In our navigation system, the real error (the TRE actually measured) did not exceed a volume of 1.58 mm³ with a probability of 0.9. A mean value of 0.8 mm (standard deviation: 0.25 mm) was found for the FRE. The quality of the coordinate tracking system (Polaris localizer) could be defined with an FLE of 0.4 ± 0.11 mm (mean ± standard deviation). The quality of the coordinates of the crosshairs of the phantom was determined with a deviation of 0.5 mm (standard deviation: 0.07 mm).

Conclusion: The results demonstrate that our newly developed ultrasound-guided navigation system shows only very small system deviations and therefore provides very accurate data for practical applications.

• Error analysis
• accuracy
• ultrasound navigated soft tissue surgery
• ENT
• reference free
• target registration error
• fiducial registration error
• fiducial localization error

View correction statement:

Erratum

Introduction

It has long been desired to improve image-guided visualization of the anatomical situation in the head and neck region during (minimally) invasive procedures, mainly because of the close proximity of vital structures [1],[2]. Conventional navigation systems for Computer Assisted Surgery (CAS) rely on preoperative computed tomography (CT) or magnetic resonance imaging (MRI) scans [3–5], which only show a “still frame” of the situation before surgery. With such systems, fiducial points (markers) are fixed to the patient before the head is scanned, and a point-based (point-pair) registration method is used: the coordinates of the markers in the strata pictures are defined manually, while the coordinates of the real markers are detected manually with the pointer. The correlation of both sets of marker values forms the basis of the registration. A visual verification of the registration is also performed (if, for instance, the pointer points to the tip of the nose, the cursor on the monitor will appear in the corresponding layer of the CT or MRI data). The definition of accuracy for such navigation systems is based on evaluating the Fiducial Localization Error (FLE), the Fiducial Registration Error (FRE) and the Target Registration Error (TRE).

An important drawback of this procedure is the fact that it is a “static” and not a “dynamic” visualization [6]. Changes that occur during or as a result of surgical interventions cannot be shown. Furthermore, such procedures can only be executed in close relation to bone structures serving as landmarks. If surgery is performed in soft tissues far away from any such landmarks, navigation will become very inaccurate because of so-called “tissue shift” [7].

Here, sonographically assisted navigation systems offer an alternative. The primary advantage of sonography is its “dynamic” character [8–10], enabling immediate visualization of tissue changes during surgery. Fortunately, sonography is a relatively cheap, easy to handle and radiation-free method with high resolution and good depth penetration [11],[12]. The navigation system described in this paper is based on a navigated ultrasound scanner and a navigated instrument. Its special feature is that there is no requirement for prior acquisition of CT or MRI scans of the patient with fiducial markers in place. Instead, the anatomy is visualized in real time by a navigated ultrasound probe.

An alternative to ultrasound data acquisition is the use of intraoperative MRI or CT equipment, which enables the image data to be updated periodically during the procedure. However, real-time sonography has the advantage of being able to provide continuous updates without involving any radiation exposure, though it should be noted that availability of the radiation-free option of intraoperative MRI (e.g., using the O-arm™ Imaging System by Medtronic) is increasing.

In this paper we describe an error analysis specially developed to determine the accuracy of our ultrasound navigation system. It is a modification of the already established error assessment for navigation (CAS) systems based on CT or MRI: FLE (Fiducial Localization Error) is the possible error in localizing the registration points; FRE (Fiducial Registration Error) is defined as a possibly erroneous distance between registration points in reality and in the scan; and TRE (Target Registration Error) defines the distance between corresponding points within the operating field that were not used for the registration. For the error analysis, a point-pair registration was performed by means of a marker plate over four points (markers). The coordinates of the markers in the ultrasound image were registered with mouse clicks, while the actual ones were registered manually and then acquired with the reference rigid body. The registration was performed by means of correlating marker (pair-) points.

Error definition for the point-based registration method in CT- or MRI-aided navigation

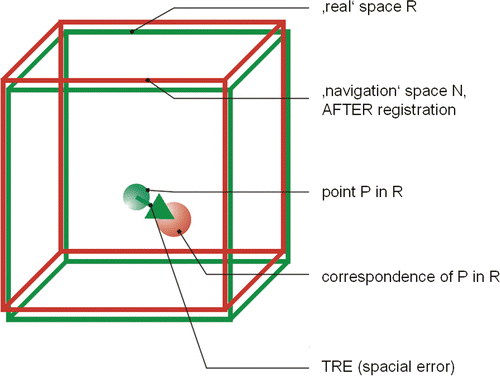
Registration plays a crucial role in medical navigation. There are two “spaces” in image-supported navigation: the picture created by the visualization method, e.g., MRI or CT, and the navigation space represented by the coordinate tracker. However, image information can only be used for navigation when a correlation between these two “worlds” or “spaces” is known. Markers can then be registered that are realized in both systems. The description of the same physical markers from the perspective of two different coordinate systems (see Figure 1) principally allows the calculation of a correlation between these two coordinate systems. In a three-dimensional (3D) space, at least three markers have to be taken into account [5]. In this paper, only Cartesian coordinate systems with orthonormal coordinate axes in a 3D space will be considered. The correlation between two coordinate systems expresses itself mathematically in the form of a 4 × 4 transformation matrix, consisting of a rotation aspect and a translation aspect. The action of calculating this transformation matrix is called registration.

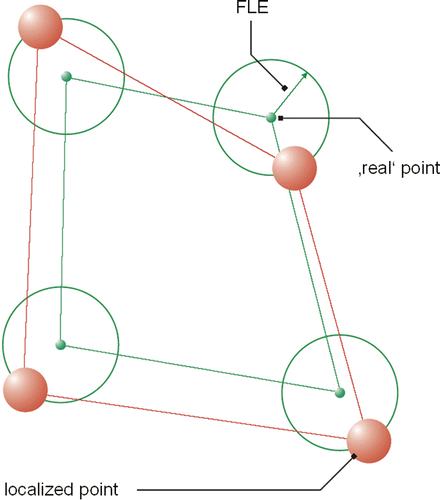
Figure 1. Graphical representation of the test method. The registered coordinates from two different coordinate systems are made congruent. The 3D error (distance) of two corresponding points is calculated.

The basic problem of registration is the technical capture of the marker positions in space. Irrespective of the technology used, every measuring device is subject to several errors which cause aberrations in the measured readings compared to the real values. It is therefore impossible to calculate a transformation that flawlessly makes markers from the first coordinate system and those from the second coordinate system congruent. That is why a “best fit” algorithm is used to calculate transformations: “best fit” describes the transformation that constructs a congruency of the marker positions in two coordinate systems with the least possible discrepancy between the corresponding marker positions in both systems. That is, the transformed points do not describe the second coordinate system, but rather a “best fit” coordinate system which approximates to the second system as well as possible with respect to all six degrees of freedom. In this best possible approximation, the relative distances of the markers are preserved. As shown in Figure 1, the registration describes a “best fit” coordinate system, which is not exactly identical to either coordinate system. Rather, the markers are defined by this “best fit” coordinate system in an “averaged” position. However, “averaged” in this case must be understood as indicating not an arithmetical mean value, but the position with the least possible registration error.

As previously explained, the assessment of accuracy of navigation systems is based on the calculation of the Fiducial Localization Error (FLE), the Fiducial Registration Error (FRE) and the Target Registration Error (TRE) [13]. An important factor in the calculation of the FLE and FRE is the Root Mean Square (RMS) value, defined aswhere RMS is the root mean square, n the number of measurements, x the arithmetical mean of the results (in mm) and x_i the results (in mm).

FLE

This is the error resulting from locating the fiducial points with the Polaris localizer. In terms of figures, this is a single error per marker used (see Figure 2). If, for instance, a measurement uses four markers, this may result in four errors. In the literature [14], a difference vector between real and measured points has sometimes been used. To reduce this swarm of errors to a single figure, we will consider the RMS value of all vector components in this paper. Thus, this value is clearly illustrated as the radius around the actual point within which approximately 66% of all registered points are situated. Factors possibly influencing FLE are the position of the spheres in the passive rigid body of the instrument, the technical accuracy of the Polaris localizer, and the calibration accuracy of the ultrasound scanner.

Figure 2. Fiducial localization error (FLE), which is the error in locating the fiducial points.

FRE

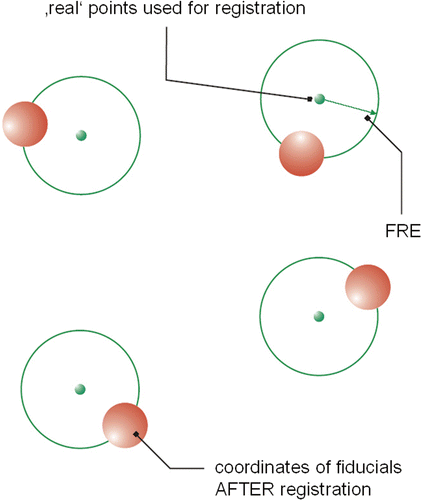
The FRE is defined as the distance between corresponding registration points in the image and in reality. The FRE error analysis is based on the methods of CT- or MRI-based navigation, i.e., the safe and precise transfer of preoperatively measured image data (CT or MRI) into the intraoperative situation [15]. For the “fiducial registration”, the markers are scanned along with the patient and should be clearly visible in the stratigraphic scans. The same markers are again addressed intraoperatively with a pointer in the course of the relevant registration. A comparison of the marker point location within the image and the coordinates freshly registered with the pointer enables correlation of the images to the navigation system. To investigate the accuracy of our navigation system, scans of a test body were taken. The test body was then registered manually in the navigation system, with the defined test points being addressed with a pointer. As the exact position of the markers was known, a comparison of the position of the freshly recorded points relative to one another gave evidence of the registration quality. The “quality of registration” indicates the accuracy with which a “best fit” algorithm matches the virtual (image) and real markers (see Figure 3). An RMS value may be formed from these values, which corresponds to the FRE.

Figure 3. Fiducial registration error (FRE), which is the distance between corresponding fiducial points after registration.

TRE and TTRE

TRE is the distance between corresponding points other than the fiducial points after registration, that is, the error definition for any point of the system, and reflects the error that is relevant for surgical applications. It has been shown that this error depends on the distance to the center of the marker used for registration and its position in space [16] (see Figure 4). The term “target” here refers to the direct association to the target point of the tracing procedure. It is practically impossible to determine the TRE directly intraoperatively, as no additional markers are applied to the patient: To completely investigate the TRE, an infinite number of markers would be necessary. Instead, the surgeon must rely on statistical error predictions, which are either definable based on the knowledge of the position accuracy of the registration points (RMS[FLE]) or measurable by adjustment of the registration points (RMS[FRE]).

Figure 4. Target registration error (TRE), which is the distance between corresponding points other than the fiducial points after registration.

The theoretical TRE (TTRE) is a value calculated for any point from the registration matrix that is not used for registration [17]. Given that the real TRE cannot be calculated intraoperatively, it is always necessary to investigate in vitro (i.e., in the laboratory) whether the real TRE may be used instead of the TTRE. It is therefore obligatory to compare the real TRE with the TTRE and quote the difference.

The FRE comprises registration errors as well as all FLE errors. Errors influencing the precision of the pointer and the ultrasound probe directly influence the registration process and its accuracy. As the FRE comprises the FLEs, so the TRE comprises the FLE and the FRE.

The objective of this article is to transpose the error description of our navigation system, originally developed for CT-based navigation, to applications in soft tissue surgery as well.

The ultrasound-aided navigation system

Any sonographically aided target approach for a surgical instrument in the head and neck region has to fulfil the following requirements [18],[19]:

1. Real-time visualization and verification of the individual anatomy based on ultrasound data [20],[21].

2. Planning and indication of an intervention access path (with a choice of alternative access paths) with respect to entry point and inclination of the surgical instrument, while taking into account the need to protect neighboring structures.

3. Permanent verification of the position of the surgical instrument relative to the target structure.

Components of the navigation system

Ultrasound device, navigated ultrasound probe, navigated instrument

A conventional ultrasound system (Echo Blaster 128 INT-1Z, Telemed, Lithuania) with a 9-MHz linear probe and 40-mm field of view was used. The ultrasound probe has an interface to a rigid body for navigation, the position of which is kept stable by a fixed holder. Thus, only one calibration process is necessary; the data recorded are saved in the storage device and can be fallen back on at any time. A passive rigid body was used for the calibration device as well as for the ultrasound scanner.

Navigated puncture device

A commercial device for fine needle punctures (Cameco Ltd., London, UK) was combined with a fixture and an interface to the sender. A 10-ml syringe (B. Braun Melsungen AG, Melsungen, Germany) was combined with a 20 G needle (BD Microlance, Fraga, Spain) and fixed to the puncturing device. Prior to application, this appliance was calibrated.

PC and software

Hardware was a Dell Latitude D620 computer featuring Intel Core Duo T2300E, 1.66 GHz, 1 GB RAM, MS Windows XP, NVIDIA Quadro NVS 100M graphics card, and MS Visual Studio C++. Custom software was developed for the calibration process, as well as for practical use in surgery. This enables the presentation of a real-time digitalized ultrasound image on the screen, with the length units converted into millimeters.

Coordinate tracker

Target accuracy was determined with a coordinate tracker using the Polaris system (Northern Digital Inc., Waterloo, Ontario, Canada). The system's inherent accuracy for finding a spot in a 3D room is 0.24 mm. This value is registered as the FLE of the coordinate tracker.

Calibration of the ultrasound probe

Calibration is necessary to adjust the two-dimensional (2D) ultrasound image of the navigated scanner to the coordinates of navigation [22],[23]. We used the Polaris system as a video-optical coordinate tracker. The calibration process is based on the use of a calibration body with fixed passive rigid bodies (see Figure 7). This calibration body contains nine 0.04 mm filaments (fishing line threads) arranged in the form of an N in three different, parallel planes. The exact position of these threads was ascertained previously with a UMM 850 coordinate measuring machine (Carl Zeiss AG, Oberkochen, Germany). The exact positions of the calibration body and the transducer were then conveyed to the coordinate tracker. The calibration body was immersed in a tank of water at 37°C. The threads of the calibration body were visible in the ultrasonic picture, and the measured distances of the crossing points allowed a precise determination of the position of the ultrasound probe.

Visualization and practical application

The greatest challenge encountered in sonographically controlled invasive procedures with a surgical instrument (a puncture needle, for instance) is the adequate representation of the instrument tip in the 2D image. This tip can only be visualized correctly when it is exactly in the image plane [24] (Figure 5). This difficulty is overcome by a method we call sonographically navigated surgery [25]. Combining a navigating ultrasound scanner with a navigated puncture device allows visualization of the 3D relationship between the needle tip and the anatomy at any time during the procedure. This is achieved by real-time integration of the needle tip position (3D data set) into the ultrasound image (see Figure 6). A navigation system allows alignment of the needle with respect to insertion angle and insertion depth even before actually perforating the skin (see Figures 7 and 8). The “virtually prolonged” tip enables the planning of the least traumatizing insertion path to the target structure. Thus, the tip of the instrument approaches the target structure very precisely. The navigation system also provides information on the direction of the instrument and the distance of its tip from the target point.

Figure 5. Three-dimensional space and a 2D ultrasound image. Blue: Behind the plane–the instrument is visible, but the instrument tip is not visible. Red: Above the plane–neither the instrument nor its tip are visible. Green: Exactly in the plane–the instrument tip is visible.

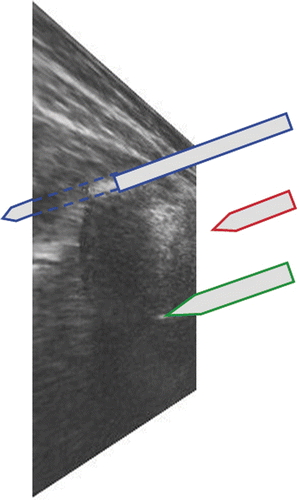
Figure 6. The position of the instrument tip (3D dataset) is integrated simultaneously into the 2D dataset of the ultrasound image. The instrument tip is visible in the ultrasound scan. The right bar and arrow indicate the trajectory of the instrument in the side view (up/down). The lower bar and arrow indicate the trajectory of the instrument in the top view (left/right).

Figure 7. Calibration procedure. Left: Calibration body and navigated ultrasound probe. Right: The ultrasonic image shows the “N-shaped” filaments in the calibration body. The exact position of the ultrasound probe in relation to the calibration body can be determined from the distances of the points from one another using a contour-seeking algorithm.

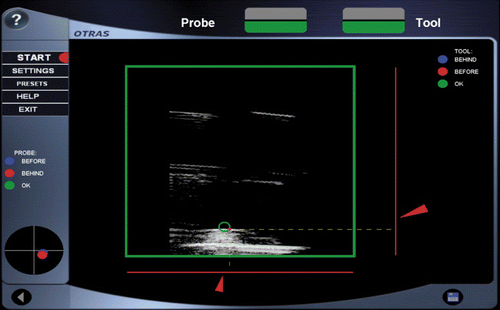
Figure 8. Target structure in the ultrasound image (green circle). The red navigation aids (bars, arrows, point) indicate the distance to the target structure and the proposed insertion channel for the surgical instrument. When the target has been successfully touched, the color of the navigation aids will change to green.

Error definition and error analysis for the ultrasound-aided navigation system

Based on the error analysis for point-related registration methods in CT- or MRI-based navigation described above [26],[27], we conducted an error analysis of our newly developed prototype for real-time sonography in the head and neck region.

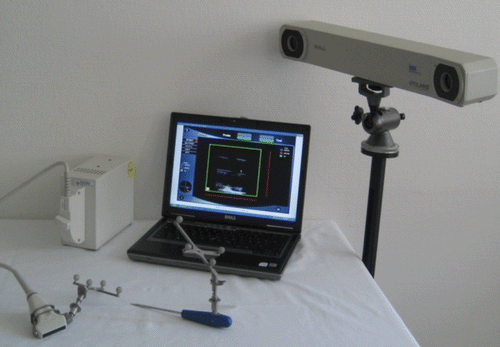
The aim of these efforts was to develop a method to define the accuracy of our ultrasound-based navigation system. Digital measurements of a test body (a marker plate) have to be possible, and the “human error” factor (in scanning, registration, etc.) must be minimized. The error analysis was performed in a test setup (see Figure 9), because the navigation method described does not require a point-pair registration.

Figure 9. Components for sononavigation: ultrasound device with navigated scanner (left), navigated pointer, PC with custom software (center), and Polaris coordinate tracker (right).

Measuring devices

Marker

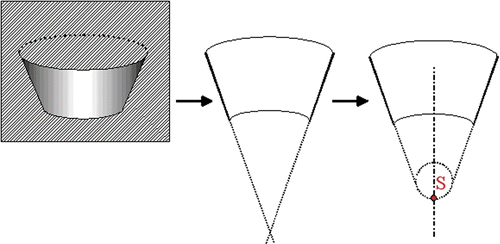
Exactly defined marking is indispensable in order to be able to visualize a point on the screen and steer for this point in reality (see Figure 10). This marking is sine qua non for a precise registration. The marker features a small indentation with a very exactly defined deepest point (S). Furthermore, the geometry of the calibration body must allow this deepest point to be reached by a pointer.

Figure 10. CAD illustration of the new marker. The centre of gravity (S) of this structure lies at the deepest point of the hollow cone. When the apex of this indentation is visible there is a typical ultrasound reflection.

Stepper motor activated verification device

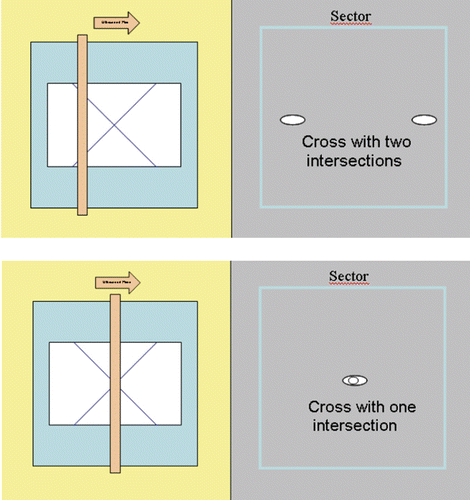
The navigating ultrasound scanner is fixed to an autonomously steered stepper motor system and immersed in a water tank at a temperature of 37°C (Figure 11). A metal plate showing a defined geometry of crossing lines is integrated into the system. The ultrasound scanner was advanced step-wise to the points of intersection until the crossing point was reached (Figure 12). An additional task was to determine the accuracy of the ultrasound image even in those regions not directly focussed on by the scanner. We therefore defined five sectors of the ultrasonic image and conducted additional measurements as described above (definition of intersection points). Identification of outlines and calculation of point areas were accomplished by means of a specially developed algorithm. The values found indicate how precisely a point in the ultrasound image was found.

Figure 11. Stepper motor device for verification of the ultrasound probe. The three motors move the test probe along the x-, y- and z-axes in relation to the reference to reach the exact point of intersection.

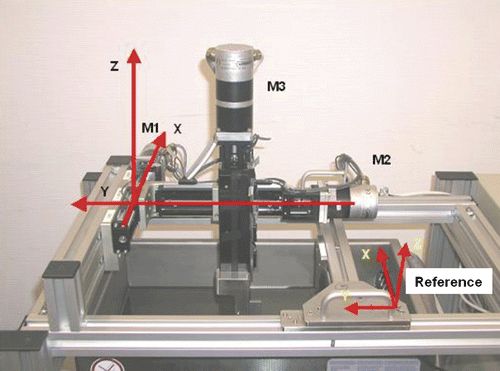
Figure 12. By means of a stepper motor verification device, the ultrasound probe was advanced to the point of intersection of the lines (given geography on a metal plate). In the upper panel the ultrasonic plane does not lie in the intersection region of the lines. In the lower panel the point of intersection has been found.

Marker plate for registration

An 80 mm × 80 mm plate (Figure 13) with ten glued-on markers was fixed in a rigid fixture and connected with an interface to the rigid body. Four markers were used for registration; the other six served to determine the TRE. Before application, a measurement was made with the coordinate measuring machine (CMM) to obtain a standard of comparison.

Figure 13. Marker plate with ten reference points.

Interpretation procedure

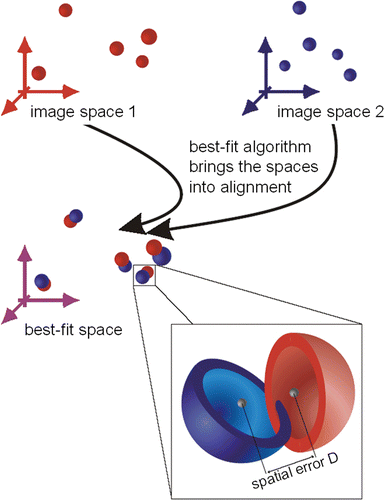
The interpretation takes into consideration five different data sets. It must be kept in mind that these data do not exist in the same coordinate system. If we wish to compare the coordinates, the different coordinate systems (image spaces) must be made congruent as thoroughly as possible. This is achieved by summing the distances of two corresponding (pair-) points (point 2 of image space A and point 2 of image space B). The “best fit” state is defined as the smallest value for the sum of differences. To reach this “best fit” (see Figure 1), we used the ITRQ3d algorithm (Northern Digital Inc.) [28]. The result will be the absolute spatial error, that is, the mean distance of the corresponding points (see Figure 1), which can be expressed as RMS error.

Ultrasound image plane data

Data collected in the calibration process were verified by means of the stepper motor activated verification device in a tank of water at 37°C. In this device, five positions were registered. As these data were to be located in the ultrasound plane, we call them image plane data. The calibration data describe the transformation between the adapter of the rigid body and the ultrasound image plane.

Thread phantom data from measuring room

The coordinates of intersection points of the thread phantom were measured with a UMM 850 coordinate measuring machine (Carl Zeiss, Inc., Jena, Germany) in the fine measuring room of Aesculap AG. Five such locations were registered.

Marker plate data from measuring room

The coordinates of the deepest points of the plate's cone-shaped markers were registered with the coordinate measuring machine in the fine measuring laboratory of Aesculap AG. This machine allows accuracy down to 2 µm. Thus, the difference from the accuracy of the Polaris localizer is sufficiently high that we can neglect the error of reference data collection. As we were only interested in the 3D position of the cone and not its actual dimensions, only the inner surface of the cone was measured (see Figure 14). These data from the fine measuring laboratory were transferred into a CAD system, and the inner cone surface was cut by a plane through the symmetry axis of the cone. By extending the resulting lines to their point of intersection we found the exact position of the deepest marker point. However, as the real marker points show a radius of 0.7 mm at the deepest point, the tip was rounded accordingly. The coordinates to be used for reference derive from the deepest point of the cone (the apex) and correspond to the center of gravity of the marker.

Figure 14. The apex S (deepest central point) is calculated from the cone surface.

Coordinate tracker data

We performed ten measurements over ten markers of the marker plate. For each measurement, the cone apex coordinates of the marker plate for all ten markers within the Polaris localizer's coordinate system were registered by a pointer.

Sononavigation data

The second method of registering the cone apex of the marker plate was the algorithm for navigated real-time sonography described above (see section headed The ultrasound-aided navigation system). The markers were always registered at the deepest point (apex) of the cone (see Figure 10).

Analysis of FLE

Quality investigation of the coordinate tracker

A marker plate was used to investigate the accuracy of the coordinate tracker (see Figure 13). First, we registered the marker plate data in the fine measuring lab and the coordinate tracker data. As they are not positioned in the same coordinate system, these coordinates were made thoroughly congruent for comparison (see also the Interpretation procedure sub-section). Finally, the RMS between corresponding points could be calculated.

Quality investigation of coordinates of intersection points in the thread phantom

To test the accuracy of the probe, and to allow predictions of the real tracking accuracy, possible distortions or inaccuracies of the ultrasound system, the calibration data were scrutinized. The accuracy of the ultrasound navigation was tested with the stepper motor machine (see Figure 11), with the measurements being repeated ten times. The results of these measurements were compared with the results from the fine measuring laboratory (thread phantom data). After application of the “best fit” algorithm, the first spatial differences (five distances corresponding to five positions) could be interpreted. To obtain a statistically reliable statement, a further five calibrated probes were used. In accordance with the methods described above, data sets for these probes were registered (thread phantom data and ultrasound image plane data). By means of the “best fit” procedure, all six probes were compared, so 10 × 6 vectors with three coordinates were investigated. The RMS error was equal to the FLE.

Analysis of FRE

To check the repercussions of ultrasound and real-time image generation on the overall accuracy, several registrations were performed with our real-time navigated sonography system and the marker plate on four of the ten markers. With no CT image, we registered point by point on the marker plate using real-time sonography (sononavigation data). The 3D position of the pointer or the thus-registered apex of the cone, respectively, was taken into account in this registration process. To allow for a statistically reliable statement, five registrations were performed in accordance with the above-mentioned procedure. The RMS error was equal to the FRE.

Analysis of TRE

The measurements made in these investigations were performed in a water tank. Six markers were used, other than those used for the registration process. The investigator held the navigating ultrasound scanner in one hand and the pointer in the other. The deepest point of the indentation was marked with the cursor on the screen. This marked structure was then tracked by means of a surface-seeking algorithm. Every movement of this marker point in the ultrasound image was followed by the “target point”. Without visual control, the pointer was advanced toward the target point. The virtual image of the pointer tip was shown on the display and its coordinates were transmitted to the interpretation software. Thus, after manual registration, ten measurements each were performed for six points on the marker plate that were not used for calibration. The sononavigation data and the coordinate tracker data of the six markers were used for the subsequent calculation. The results of these ten measurements were 10 × 10 vectors with three coordinates. They were interpreted with regard to the volume V(α) of the physical position in space within which the point would lie with a probability of α at each subsequent measurement. If, for example, the volume V(0.5) = 10 mm³ was calculated, the measured point of the following registration would lie within this volume with a probability of 50%.

To calculate this V(α), the α-quantiles of all measured points were determined for the x-, y- and z-coordinates, respectively. For the α-quantiles, Tα = x, where x is the value for which p(y ≤ x) = α applies, the probability of obtaining a value of y ≤ x is still α. The segments s(α)x, s(α)y and s(α)z define parts of the x-, y- or z-axis within which the coordinates of subsequently registered vectors will be located with a probability of α. As all three segments may be regarded as equivalent, it follows that the probable physical positions in space describe a cuboid. The volume of this cuboid is

The theoretical TRE was calculated with this formula to verify the statements of West and colleagues and to check their applicability within a navigation system [14],[17],[27].

Results

FLE

Quality of coordinate tracker

The ten points of the marker plate registered with the pointer (coordinate tracker data) deviated by an average of 0.4 mm from the real points registered on the plate in the fine measuring laboratory (marker plate data) (standard deviation: 0.11 mm). Thus, this results in an FLE of 0.4 ± 0.11 mm (mean ± standard deviation).

Quality of coordinates of intersection points in the thread phantom

The points of ultrasound image plane data registered with the stepper motor machine differed by a mean of 0.5 mm (standard deviation: 0.07 mm) from the values of the thread phantom data (from the measuring room).

FRE

As described above, five registrations (over four markers) on the marker plate (marker plate data) were performed. These reference points were defined with the pointer and also with the navigation software (sononavigation data). The evaluation was performed using the “best fit” procedure described above. The RMS error equals the FRE. For the FRE, a mean value of 0.8 mm (standard deviation: 0.25 mm) was calculated.

TRE

The following V(0.9) values for all six markers were calculated: 1.4, 1.8, 1.5, 1.5, 1.6 and 1.7 mm³, based on the marker plate data and the sononavigation data. The mean value is 1.58 mm³. This indicates a 90% probability that the point of a subsequent measurement will be positioned within this volume of 1.58 mm³.

The difference between TTRE and TRE for all six markers amounts to 0.14 mm when registered by the sononavigation system with pointer. Thus, the real TRE is shown to be generally smaller than the theoretical TRE.

Discussion

We have developed a navigation system for sonographically aided surgery of tumors in the head and neck region [25]. Accuracy is therefore more of a concern than would be the case in a system primarily for thoraco-abdominal interventions, for example. Both the ultrasound scanner and surgical instrument are navigated, with their 3D positions being precisely known at any time. The distance of the instrument from and its relation to the ultrasound image plane as well as to the target structure is appropriately integrated into the 2D ultrasound image. This enables an exact approach of the surgical instrument to the target structure. The advantage of this navigation method is the real-time visualization; any shifts or changes in the target structure are shown directly.

In comparison to CT- or MRI-based navigation, the ultrasound-aided system offers the following advantages:

1. Unlike conventional CAS systems, e.g., for surgery near the skull base or for bone surgery [29],[30], the application of a fixed reference rigid body to the patient's body is dispensable. This rigid body, which has to be fixed in the very vicinity of the operating site, is necessary to guarantee a safe navigation, even when the rigid body or the position of the object will shift. The navigation system described in this paper does without such a reference rigid body as the ultrasound scanner and needle are both navigated in real time. Thus, shifts in the surgical site and the changing position of the surgical instrument are visualized virtually immediately in the ultrasound image. The great advantage of this navigation method for soft tissue surgery in the neck region derives from the fact that there are no anatomical structures in close proximity to the operating site which permit a simple fixation of a reference rigid body [17].

2. This novel procedure fulfils the requirements of minimally invasive diagnostics: any surgical instrument can be advanced towards the target very safely under sonographic real-time control, and changes in the target structure are immediately visualized. This manipulation is easy, cost-effective, and avoids exposure to radiation. Any ENT professional can perform this procedure, and extensive checkups or radiological interventions (CT- or MRI-based biopsies) are no longer necessary.

3. This procedure furthermore fulfils the requirements for minimally invasive therapies. Possible future applications may be the well-targeted delivery of drugs or high-intensity focused ultrasound (HIFU): our system will provide the necessary position information for such applications.

The system was scrutinized with respect to the accuracy with which the instrument tip can approach the target. The marker plate used for this investigation was designed so as to cover a maximum volume of 50 mm × 50 mm × 20 mm, representing the normal dimensions of invasive procedure sites. All findings presented in this paper refer to this previously determined volume.

One aim of this study was to investigate the “real” error, that is, the actually measured TRE. When aiming at an error volume of 1.58 mm³, considered as good target accuracy in our system, 10% of the registered values drop out (i.e., 10% of measured points lie beyond this volume). The FLE and FRE analysis of our study allows quantitative statements as to the quality of the coordinate tracker (FLE = 0.4 ± 0.11 mm), the quality of the coordinates of the intersection points of the thread phantom (FLE = 0.5 ± 0.07 mm) and the FRE of the system (FRE = 0.8 ± 0.25 mm). These findings show the experimentally calculated error values inherent to the accuracy values of the whole system. Thus, the TRE that was actually measured comprises the FLE and FRE error values. The theoretical calculation of FLE and FRE with different methods was not the subject of this paper.

We subsequently registered the difference between the measured TRE and the theoretical TRE (TTRE). The aim here was to validate plausibly the inaccuracies of the instruments, as well as to put the TTRE at the disposal of the operator as a measure of intraoperative accuracy.

Our system works without a point-based registration as is necessary for navigation based on CT or MRI. Nevertheless, a complete laboratory registration was performed to provide accuracy information comparable to that available for a CT-based navigation.

These markers were used in an earlier study [31] for analysis of point-based registrations in computer aided head surgery (CAHS). The markers were scanned during registration and their apices calculated automatically from the gray-scale value distribution of the CT images. Stability or spread of error distances during registration could be improved considerably compared to manual registration. The TRE results of this earlier study are comparable to our results. Thus, the targeted precision of CT-based navigation yielded results comparable to those of an ultrasound-supported procedure.

As the “human factor” of imprecision in freehand registration is reduced to a minimum, the entire navigation sequence (scanning of the reference points using sononavigation software) with the marker plate can be evaluated and compared.

In summary, we may state that our newly developed ultrasound-aided navigation system produces very precise values. The system deviation for the TRE investigated does not exceed the volume of 1.58 mm³ with a probability of 0.9.

Conclusion

To analyze the cornering predictability of our novel ultrasound-based navigation system, a complete laboratory registration with subsequent error analysis has been performed. This included the determination of the FLE, FRE and TRE, using methods adapted from a point-based registration method for CT- or MRI-based navigation. The results of our research show that deviations with our new system are limited to a volume of 1.58 mm³ with a probability of 0.9. Thus, a very precise and reliable navigation system is now available for practical application.

Acknowledgments

We thank Dr. Siegwart Peters for his assistance in preparing this manuscript.