Femur statistical atlas construction based on two-level 3D non-rigid registration

Abstract

The statistical atlas is a 3D medical image analysis tool to enable more patient-oriented and efficient diagnosis. The atlas includes information on geometry and its variation across populations. The comparison with information from other patients is very useful for objective quantitative diagnosis. The statistical atlas can also be used to solve other challenging problems such as image segmentation. As a key to the construction of statistical atlases, 3D registration remains an important yet unsolved problem in the medical image field due to the geometrical complexity of anatomical shapes and the computational complexity arising from the enormous size of volume data.

In this work we developed a two-level framework to efficiently solve 3D non-rigid registration, and applied the method to the problem of constructing statistical atlases of the femur. In contrast to a general multi-resolution framework, we employed an interpolation to propagate the matching instead of repeating the registration scheme in each resolution. The registration procedure is divided into two levels: a low-resolution solution to the correspondences and mapping of surface models using Chui and Rangarajan's thin-plate spline (TPS)-based algorithm, followed by an interpolation to achieve high-resolution matching. Next, principal component analysis (PCA) is used to build the statistical atlases. Experimental results show the shape variation learned from the atlases, and also demonstrate that our method significantly improves the efficiency of registration without decreasing the accuracy of the atlases.

• Statistical atlas
• femur
• two-level
• 3D non-rigid registration

Introduction

Statistical atlases are used as references in interpreting CT and MRI images [1], and represent the shape or appearance of human anatomical structures [2], [3]. Some atlases are based on physical properties, such as elastic models [4], [5], “snakes” [6], geometric splines [7], and finite element-based models [8]. Others are modeled from the statistical perspective: Szeliski [9] introduced the statistical atlas to analyze shape variation between patients. To analyze shape and appearance variation, principal component analysis (PCA) is widely used [10], [11], [12]. The two most common statistical atlases are the shape atlas [13] and the appearance atlas [14]. The shape atlas uses only geometric information such as landmarks, surfaces (boundaries of 3D objects) or crest lines [3], while the appearance atlas uses both geometric features and the intensity of pixels or voxels.

As a key to the construction of atlases, 3D registration has been studied for many years in the context of computer vision, but remains a critical problem in the medical image field due to the geometrical complexity of anatomical shapes and the computational complexity arising from the enormous size of volume data. Three-dimensional registration has numerous clinical applications, such as statistical atlas construction for group study and statistical parameter analysis [15], [16], mapping anatomical atlases to individual patient images for disease analysis [17], [18], [19], and image segmentation [20], [21].

Depending on the type of transformation involved, registration can be rigid or non-rigid. If the shape does not change between the two images, registration should be rigid, such as in intra-subject inter-modality (same patient; different imaging system) registrations, where images are captured at the same time. However, when we take into account the time, i.e., when two images are captured at different times, as in intra-subject registrations, most are non-rigid due to the shape variation of the anatomical structures caused by swelling, prostate probing, bone fractures, tumor growth, intestinal movements and so on. In addition, inter-subject (different patients) registrations are usually non-rigid because of the local anatomic difference between patients. So far, non-rigid (or deformable) registration remains a challenging problem [22].

Non-rigid registration is used to find a non-rigid transformation from one 3D surface to the reference surface by minimizing the distance between two surfaces. In general, a non-rigid transformation is represented by a global rigid or affine transformation plus a local non-linear deformation, which can be represented by radial basis functions (RBFs) [23], octree splines [24], thin-plate splines [25], [15], geometric splines [7], finite elements [8], or free-form B-splines [12], etc. To evaluate the results of registration, different similarity measurements are selected according to the different image features and imaging modalities. For example, the sum of squared distance (SSD) is usually used for geometric features [26], but correlation coefficients (CC) [27], Ratio Image Uniformity (RIU) [28] and mutual information (MI) [29] are used for intensity features. Registration can be simplified given known correspondences, e.g., when using markers [30]; however, markers are not permissible or even available in many scenarios. Alternate estimations of correspondences and transformations are widely used for both rigid cases [26] and non-rigid cases [15], [25], [31]. Moreover, with the increase in data size and geometrical complexity, a multi-resolution strategy has been adopted for the registration framework [19], [32], [33]. Sparse matrices are also used to handle the computational complexity [34].

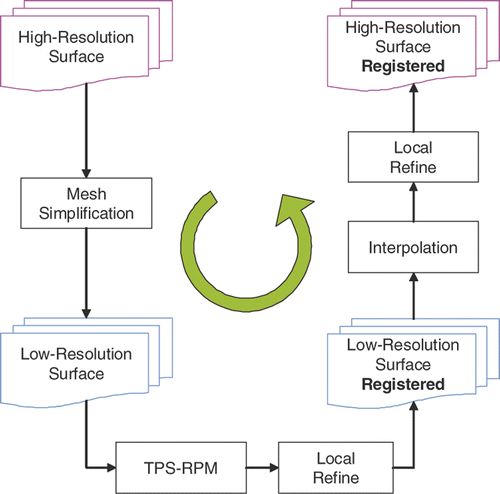
To build a femur statistical atlas given partial 3D surfaces, we developed a two-level approach inspired by Chui and Rangarajan's thin-plate spline-based algorithm [25] and the previous multi-resolution work [33]. Since Chui and Rangarajan's algorithm is unable to handle more than 2,000 3D points [34], we broke down registration into a two-level process to deal with both the computational and geometrical complexity. We first applied the algorithm to the simplified low-resolution surfaces. To improve the efficiency, instead of successively matching each resolution from coarse to fine, we directly propagated the correspondences from low resolution to high resolution by interpolation. A local refine procedure was introduced for both low-resolution and high-resolution surfaces to improve matching. Finally, we applied PCA to the aligned surfaces to construct the femur atlas. Figure 1 shows a flowchart of our two-level framework.

Figure 1. Two-level non-rigid registration framework.

Two-level framework

Mesh simplification: decreased resolution

Garland and Heckbert's quadric error metrics (QEM)-based mesh simplification [35] method was used to compute low-resolution surfaces. QEM is based on iterative contraction of vertex pairs. The cost of contraction is represented by a quadric error, and the whole process is an iterative minimization of the quadric error. Since QEM provides a fast and simple way to guide the entire process with relatively minor storage costs, the simplification step is extremely fast.

An important parameter involved in the simplification process is the number of vertices on the low-resolution surfaces. To maintain the trade-off between accuracy and efficiency, an appropriate number is selected based on a series of leave-one-out experiments (for details see the Selection of simplification parameters section below).

Low-resolution non-rigid registration: point-to-point

We applied Chui and Rangarajan's non-rigid registration method [25] to the simplified surfaces. With this method, fuzzy correspondences and a smoother optimization process can be achieved. A dual update strategy conjoined with a deterministic annealing technique is adopted to estimate the correspondences and transformation alternately. The non-rigid transformation is parameterized using thin-plate splines to generate a smooth spatial mapping.

Initial alignment

Given the particularity of the femur data, it is necessary to perform a pre-alignment to eliminate the effect caused by the missing shape. We obtained CT scans of 87 patients, all with healthy femurs, using the same scanner. As most surgeries are performed on the joints, only the top portion including the femoral head and the bottom portion including the condyles were scanned to build surfaces.

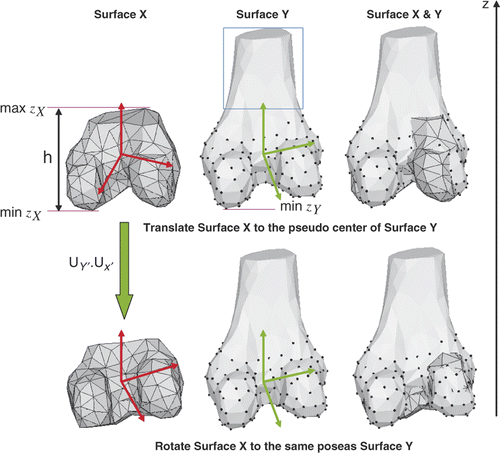
In Figure 2, the bottom portion of the femur is used as an example. It can be seen that surface Y has more femur shaft than surface X. If we were to simply align both centers as in previous work [25], experiments have shown that the registration process would be very slow and might not converge in several cases. The reason for this is that part of surface Y (bounded by blue in Figure 2) has no counterpart on surface X. Therefore, in order to improve upon the process, it was decided to estimate the pseudo-center of Y instead of the true center. The poses of the two surfaces were then estimated and aligned.

Figure 2. Illustration of the rigid transformation from surface X to surface Y. The upper row compares the translated X with Y. Black points on Y are used to compute the pseudo-center. The lower row compares the translated and rotated X with Y. Red axes represent the pose of X, green axes that of Y.

The height of X was used to estimate the pseudo-height of Y. Assuming the axis 𝒵 is in the scan direction from knee to hip, we selected those points bounded by the pseudo-height of Y (indicated in black in Figure 2) to estimate the pseudo-center κ_{Y ′} and the covariance matrices for the point set {p_X} and {p_{Y ′}}:where N_{Y ′} is the number of points {p_{Y ′}} on Y which satisfy (z_Y − min z_Y) < (max z_X − min z_X). We can solve for the principle axes by decomposing the covariance matrix using the moment analysis:

Each column of U_X represents a principle axis of the point set {p_X}, and U_{Y ′} for {p_{Y ′}}. As shown in Figure 2, three axes represent the pose of the point set: red for {p_X} and green for {p_{Y ′}}. The rotation from coordinates of X to Y ′ is computed by U_{Y ′} · U_X′. We thus applied a rigid transformation [U_{Y ′} · U_X′|(κ_{Y ′} − κ_X)] to the point set {p_X} and the two point sets were finally aligned. Experiments have shown that such alignment increases the rate of convergence from 78% to 95.2%.

Local refining procedure: point-to-surface

The result of the registration in the preceding sub-section can be further improved by minimizing the point-to-surface distance. This idea is illustrated by Figure 3. x_i is a vertex on the deformed surface X, whose corresponding vertex on surface Y is y_i. The neighboring triangles which share the same vertex y_i are S₁, S₂ and S₃. We can compute the distance from x_i to each neighboring triangle (the distance computed from the vertex x_i to the plane where the triangle lies), i.e., d₁, d₂ and d₃. If any of these is smaller than d₀ = ‖x_i − y_i‖, we use the corresponding projected point to replace y_i in order to achieve a smaller surface distance.

Figure 3. Illustration of the local refine procedure between the vertex and surface. x_i is a vertex on the deformed surface X, whose correspondence on the surface Y is y_i. The projection of x_i to each triangle S_t sharing y_i is denoted by . d_t is the distance between x_i and (t = 1, 2, 3, …).

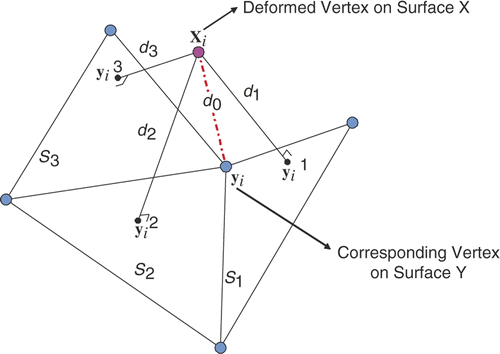
For those cases where different vertices on the surface X correspond to the same surface point on Y, we assign this corresponding surface point to the vertex on X with the smallest distance and mark it as unavailable to other vertices on X.

Low-resolution to high-resolution interpolation

Once we obtained the correspondences in low resolution (X^L and Y^L), we propagated them to high resolution (X^H and Y^H) by interpolation. The surface interpolation method is a derivative of methods known jointly as “moving least squares” [36]. Radial basis functions (RBFs), finite elements, and multivariate splines, such as thin-plate splines (2D bivariate splines) and triharmonic thin-plate splines, are popular techniques used in surface interpolation. Carr et al. [37] applied the multivariate splines method to RBFs by using splines as kernel functions. In the present work, we chose a Gaussian kernel due to its simple mathematical representation and fewer restrictions on nodes [37]. More specifically, we used a linear affine function plus a series of RBFs to construct the interpolation function:where is a vertex on the low-resolution surface X^L whose correspondence on the low-resolution surface Y^L is , i = 1, 2, …, N (N is the number of vertices on X^L). and are both 3 × 1 vectors with three coordinates. c₁ is a 3 × N coefficient matrix of RBFs. is a symmetric RBF. We selected a Gaussian kernel φ(u_i, u_j) =exp(−‖u_i − u_j‖/0.5), as suggested by Pighin et al. [38]. c₂ and c₃ are coefficients for the affine transformation. c₂ is a 3×1 vector and c₃ is a 3×3 matrix. Given N correspondences, there are N equations for each axis (𝒳, 𝒴 and 𝒵):where c₁^k, c₂^k and c₃^k denote the k^th row of c₁, c₂ and c₃, respectively. denotes the k^th row of , where k can be 1, 2 or 3, corresponding to the axes 𝒳, 𝒴, and 𝒵. There are 3N equations in total:P is a 3N × (N + 4) matrix. To ensure smooth interpolation, additional orthogonality constraints [39] were added to Equation 5, where c_1,i denotes the i^th column of c₁:

The least-squares solution for this linear system, Qc = w, is given by c = (Q^TQ)⁻¹Q^Tw.

Finally, the correspondence of a vertex in the high-resolution surface X^H can be computed by using Equation 4: , for j = 1, …, M (M is the number of vertices on X^H). We also refined the resulted high-resolution surface by the procedure described in the preceding sub-section.

Femur atlas construction

Given the aligned surfaces, rigid pose alignments are applied to eliminate the effect of imaging poses [40] prior to atlas construction. Suppose we have K aligned surfaces and each surface is represented by a 3M × 1 vector v_i(i = 1, …, K), where M is the number of points on each surface and 3 denotes three coordinates 𝒳, 𝒴, and 𝒵. We compute the mean vector κ and covariance matrix Ψ, and then apply PCA to the data set:

Therefore, any surface model in the data set can be represented by a mean vector plus a linear combination of principal components (modes):where η_i is a K × 1 coefficient vector obtained by projecting v_i onto each principal axis. New surface models not included in the data set can be generated by manipulating the coefficient η_i.

Selection of simplification parameters

In the two-level framework, the resolution of the simplified surfaces affects the final result. The smaller the number of points, the faster low-resolution registration is achieved, but results for high-resolution registration are less accurate. To maintain both accuracy and efficiency, an appropriate number is selected based on a series of leave-one-out experiments. For some extreme cases with symmetry shapes, fewer points may result in a perfect match in the low-resolution registration but a misalignment in the high-resolution registration. Therefore, not only the resolution parameter but also some landmarks are necessary to handle such ambiguity. Since the shape of the femur is already complex enough, we do not consider such extreme situations, and thus do not require any landmarks in our method.

Let denote the number of vertices on the low-resolution surfaces. For each surface v_i(i = 1, …, K), K = 87, we used other K − 1 surfaces to construct the atlas using Equations 8 and 9. Let denote the first S columns of the principal component matrix U_i, which constitutes 95% of the shape variation. Then, v_i(i = 1, …, K) can be reconstructed by this atlas:

We compared the surface distance between the original surface v_i and the reconstructed surface by computing the surface mean error and root mean square (RMS) error. We repeated this procedure for each surface and computed the average mean error and RMS error based on K leave-one-out experiments:

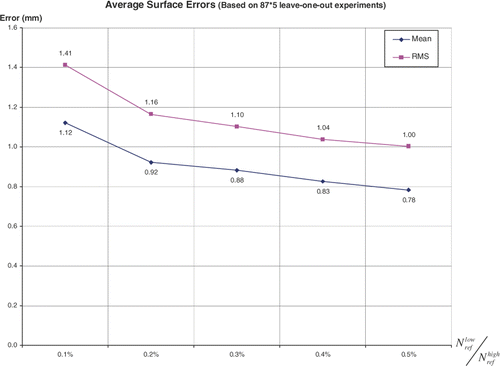
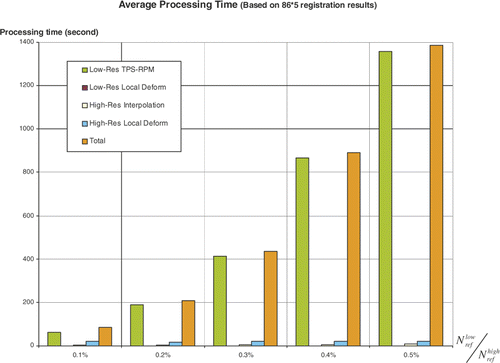
By tuning the number , we compared the error and and processing time for the two-level registration as well. Figure 5 shows when , will be less than 1 mm, which is a practical number for clinical applications. Figure 6 shows that when , the average processing time for the two-level registration will exceed 5 minutes (using a 2.4-GHz Pentium PC with 1 GB of RAM). Therefore, was finally used in our algorithm to construct femur atlases and estimate the error distributions illustrated in Figure 13.

Experiments and discussion

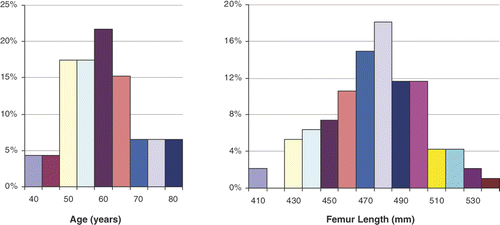
Over a period of several years, we obtained CT scans of 87 patients, all with healthy femurs, at the West Pennsylvania Hospital and Shadyside Hospital in Pittsburgh, Pennsylvania. The patients comprised 53 males and 34 females ranging in age from 39 to 78 years old; 43 left femurs and 44 right femurs were scanned, and the femur length ranged from 400 mm to 540 mm (Figure 4 shows the data distribution in terms of age and femur length). The CT volumes were segmented to provide triangulated surface models using the Marching Cubes (MC) algorithm. All surface models were smoothed by the method proposed in reference [41]. Given that most surgeries are performed on the joints, only the top portion including the femoral head and the bottom portion including the condyles were scanned to build surfaces. As a result, each set of femur data comprised two separated surfaces containing the femoral head and condyles, respectively.

Figure 4. Patient data distributions in terms of age and femur length.

Figure 5. Reconstruction errors and in terms of .

Figure 6. Processing time in terms of .

Evaluation of two-level registration

Figures 7–12 show an example of how the surface distance is decreased at each step of the two-level framework. Here we use the bottom portion of the femur as an example, given its important relationship with the knee. In this case, there are two high-resolution surfaces X^H (21,130 vertices, 42,256 triangles, 65.8 mm in the z-axis) and Y^H (26,652 vertices, 53,300 triangles, 105.9 mm in the z-axis) (Patient X was a 79-year-old female with femur length of 472.6 mm; Patient Y was a 53-year-old female with femur length of 477.6 mm). We first computed the point-to-surface distance from X^H to Y^H [42]:where ‖ · ‖₂ is the Euclidean norm. The HSV (hue, saturation, value) color of each vertex on X ^H denotes the distance d(p, Y^H). We also computed the mean error d_m(X ^H, Y ^H) and root mean square error d_RMS(X ^H, Y^H) between X ^H and Y ^H based on Equation 13:

1. Figure 7 shows the high-resolution surfaces X^H and Y^H. With respect to the bounding box diagonal of Y^H (158.5 mm), the mean error is 6.49% and the root mean square error is 7.70%.

2. Figure 8 shows the low-resolution surfaces X^L (169 vertices, 334 triangles) and Y^L (213 vertices, 422 triangles) after simplification. With respect to the bounding box diagonal of Y^L (158.3 mm), the mean error is 6.53% and the root mean square error is 7.74%.

3. Figure 9 shows the deformed low-resolution surfaces X^L(1) and Y^L after applying Chui and Rangarajan's non-rigid registration [25] to X^L. With respect to the bounding box diagonal of Y^L, the mean error is 1.68% and the root mean square error is 2.13%. The surface distance has been significantly decreased by applying Chui and Rangarajan's method.

4. Figure 10 shows the deformed low-resolution surfaces X^L(2) and Y^L after applying a local refine process to X^L(1). With respect to the bounding box diagonal of Y^L, the mean error is 0.68% and the root mean square error is 1.42%, which shows that the local point-to-surface refining procedure can further decrease the surface distance.

5. Figure 11 shows the interpolated high-resolution surfaces X^H(1) and Y^H after applying the interpolation to X^H. With respect to the bounding box diagonal of Y^H, the mean error is 1.65% and the root mean square error is 2.10%. The surface distance slightly increases by interpolation because only 0.80% of the vertices on X^H(1) have correspondences computed from low-resolution registration; the other correspondences were obtained by interpolation.

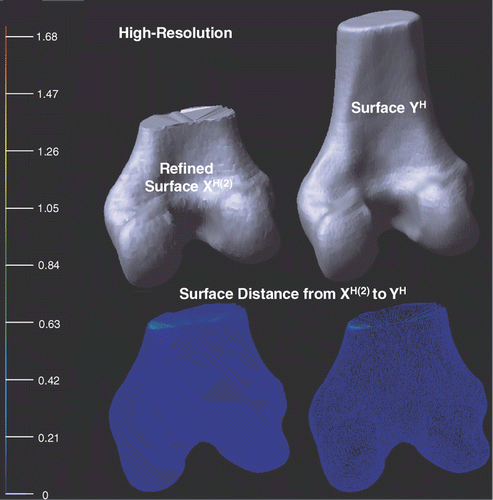
6. Figure 12 shows the deformed high-resolution surfaces X^H(2) and Y^H after applying a local refining process to X^H(1). With respect to the bounding box diagonal of Y^H, the mean error is 0.28% and the root mean square error is 1.26%, once again demonstrating that local point-to-surface refining procedure is helpful for decreasing surface distance.

Figure 7. Illustration of the high-resolution surfaces X^H and Y^H. Point-to-surface distances from X^H to Y^H are illustrated by an HSV color map: the color of each vertex on X^H represents the distance d(p, Y^H), p ∈ X^H. Both surface (left) and mesh (right) are shown on the bottom row.

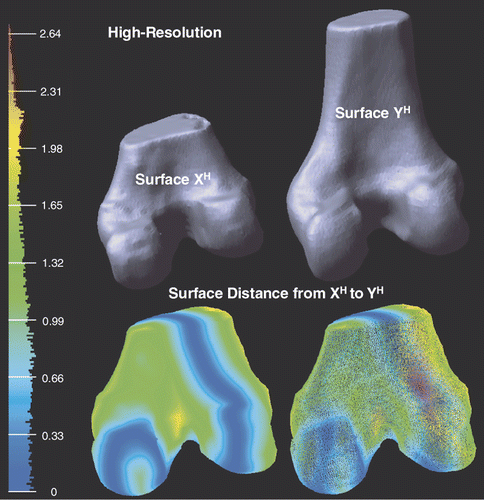
Figure 8. Illustration of the low-resolution surfaces X^L and Y^L after applying the mesh simplification (see Mesh simplification sub-section) to both X^H and Y^H. Point-to-surface distances from X^L to Y^L are illustrated by an HSV color map: the color of each vertex on X^L represents the distance d(p, Y^L), p ∈ X^L. Both surface (left) and mesh (right) display modes are shown on the bottom row.

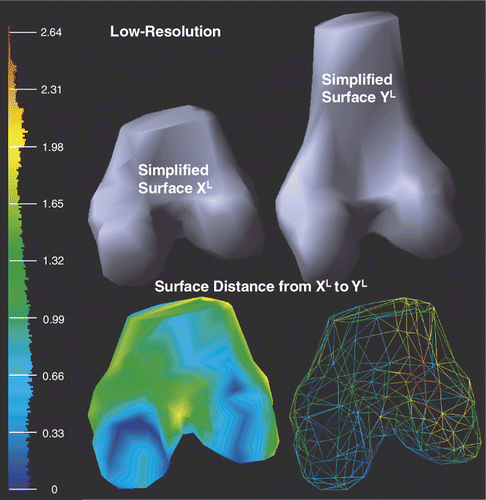
Figure 9. Illustration of the deformed low-resolution surfaces X^L(1) and Y^L after applying Chui and Rangarajan's non-rigid registration method (see Low-resolution non-rigid registration sub-section) to X^L. Point-to-surface distances from X^L(1) to Y^L are illustrated by an HSV color map: the color of each vertex on X^L(1) represents the distance d(p, Y^L), p ∈ X^L(1). Both surface (left) and mesh (right) display modes are shown on the bottom row.

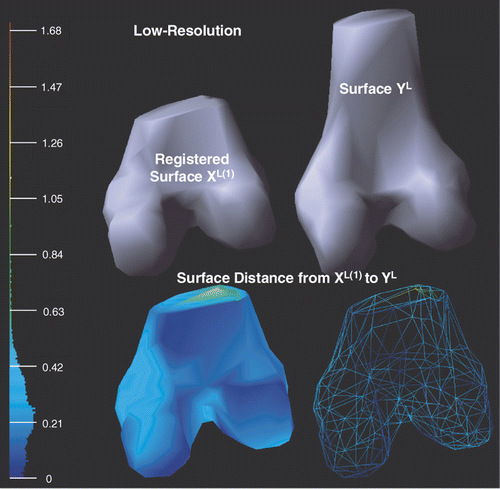
Figure 10. Illustration of the deformed low-resolution surfaces X^L(2) and Y^L after applying the local refinement (see Local refining procedure sub-section) to X^L(1). Point-to-surface distances from X^L(2) to Y^L are illustrated by an HSV color map: the color of each vertex on X^L(2) represents the distance d(p, Y^L), p ∈ X^L(2). Both surface (left) and mesh (right) display modes are shown on the bottom row.

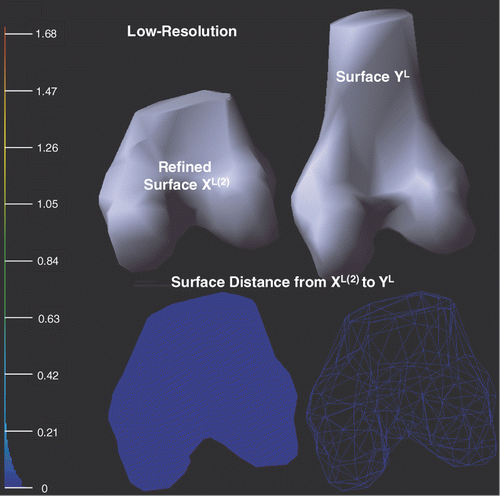
Figure 11. Illustration of the deformed high-resolution surfaces X^H(1) and Y^H after applying the interpolation (see Low-resolution to high-resolution interpolation sub-section) to X^H. Point-to-surface distances from X^H(1) to Y^H are illustrated by an HSV color map: the color of each vertex on X^H(1) represents the distance d(p, Y^H), p ∈ X^H(1). Both surface (left) and mesh (right) display modes are shown on the bottom row.

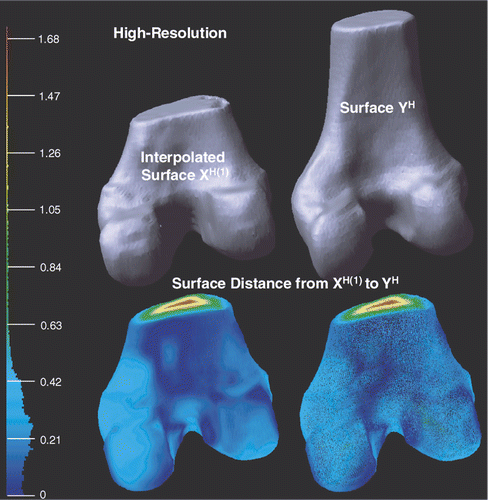
Figure 12. Illustration of the deformed high-resolution surfaces X^H(2) and Y^H after applying the local refinement (see Local refine procedure sub-section) to X^H(1). Point-to-surface distances from X^H(2) to Y^H are illustrated by an HSV color map: the color of each vertex on X^H(2) represents the distance d(p, Y^H), p ∈ X^H(2). Both surface (left) and mesh (right) display modes are shown on the bottom row.

Comparison to other registration methods

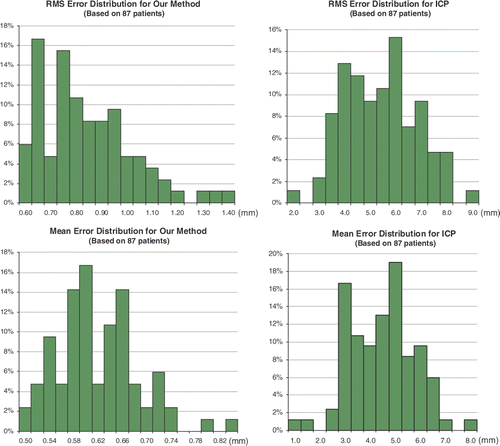
We compared our registration algorithm with the classical iterative closet point (ICP) method since the latter is widely used in many medical image registration problems. Given 87 training surfaces, the distributions of the RMS error and mean error of the two approaches are shown in Figure 13. For the RMS error, the distribution is centered between 0.6 and 1.0 mm (max: 1.4 mm) with our method, but with ICP the range is between 3.1 and 6.5 mm (max: 8.5 mm). For the mean error, the distribution is centered between 0.5 and 0.7 mm (max: 0.9 mm) with our method, but with ICP the range is 2.5 to 6.5 mm (max: 7.5 mm). From this it is apparent that the two-level non-rigid registration has a better performance than ICP.

Figure 13. RMS and mean error distributions for our method and for ICP.

Since Chui and Rangarajan's thin-plate spline (TPS)-based method cannot deal with the complexity of our data, it is not possible to compare the two methods directly. Alternatively, it can be seen from Figure 6 that our method only requires 5 min or less to match any size of surfaces with less than 200,000 vertices. In contrast, the method of Chui and Rangarajan takes 5 min for 350 vertices, 10 min for 460 vertices, 20 min for 610 vertices, and so on. It is therefore clear that our algorithm represents a significant improvement in efficiency. To maintain a good level of accuracy for practical applications, a best simplification parameter was selected based on a series of leave-one-out experiments (see details in Selection of simplification parameters section).

Evaluation of atlases

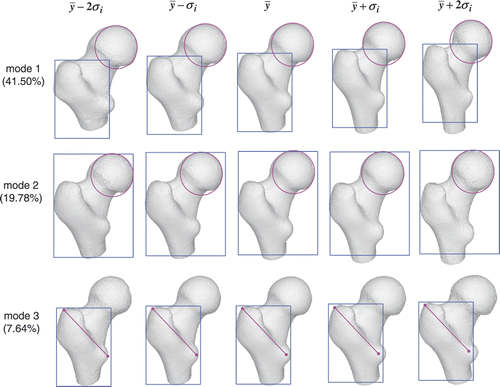
We built three atlases for the femoral head, the condyles and the entire femur. Figure 14 shows the shape variation in the first three modes of the femoral head atlas. The pink and blue shapes are used to highlight the local variation. For example, the size of the femoral head (denoted by the pink circle) gradually reduces along the first mode, but remains almost unchanged along the second mode. The greater trochanter (denoted by the blue rectangle) becomes longer but progressively narrower along the first mode, whereas it remains the same length but becomes progressively wider along the third mode.

Figure 14. Femoral head atlas: illustration of the shape variation in the first, second and third modes. The first mode encodes 41.50% of the shape variation, while the second and third modes encode 19.78% and 7.64% of the shape variation, respectively. The color shapes highlight the local shape variation.

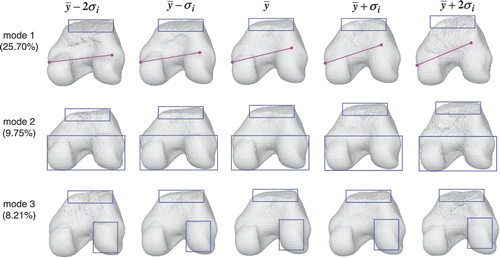
Figure 15 shows the shape variation in the first three modes of the condyle atlas. We noticed that the top of the condyles (denoted by the blue rectangles) changed considerably along each mode. This is because each scan was cut differently. The top area can only be estimated from the reference surface without any refining from the original surfaces. The lateral epicondyle (on the right) becomes progressively larger along the first mode, compared to the medial epicondyle (on the left). This is similar to the trend seen in the third mode but the change is smaller; the condyles become progressively longer but narrower along the second mode.

Figure 15. Condyle atlas: illustration of the shape variation in the first, second and third modes. The first mode encodes 25.70% of the shape variation, while the second and third modes encode 9.75% and 8.21% of the shape variation, respectively. The color shapes highlight the local shape variation.

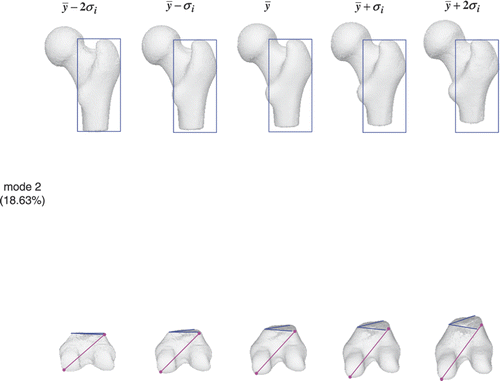
Figures 16 and 17 show the shape variation in the first two modes of the entire femur atlas. For the first mode, the femoral head and greater trochanter exhibit a similar change to that shown in Figure 14, while the condyles become progressively longer and narrower as in Figure 15. The atlas of the entire femur behaves in a manner similar to that of the individual portion in the first mode. For the second mode, the greater trochanter becomes shorter but remains the same as in Figure 14, while the condyles become much longer but keep the same length as in Figure 15. This means that the second dominant mode in the individual atlas may not be the second dominant mode in the conjunction case.

Figure 16. Femur atlas: 27.67% of the shape variation is encoded in the first mode. The color shapes highlight the local shape variation.

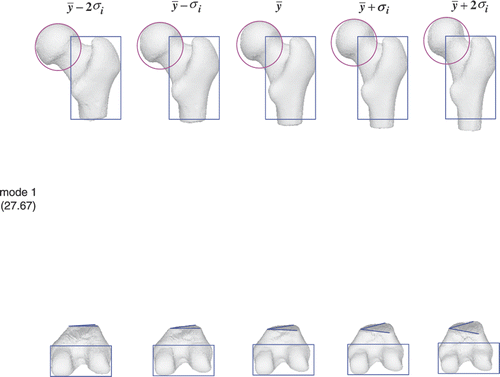
Figure 17. Femur atlas: 18.63% of the shape variation is encoded in the second mode. The color shapes highlight the local shape variation.

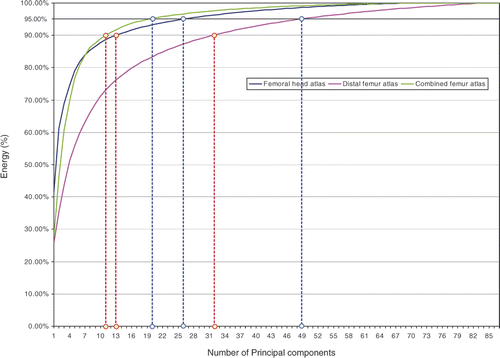
Figure 18 shows the shape variation encoded in the modes of each atlas. To keep 95% of the shape variation we only need 26 modes for the femoral head atlas, 49 modes for the condyle atlas, and 20 modes for the entire femur atlas. The condyle atlas needs more modes to retain most of the shape variation because the training surfaces of the bottom portion of the femur change shape considerably (i.e., each surface contains a different length of femur shaft).

Figure 18. Illustration of the shape variation encoded in the modes of the femoral head atlas (blue), condyle atlas (pink) and entire femur atlas (green).

Conclusion

In this paper we have developed a two-level framework to efficiently tackle non-rigid registration challenges caused by geometrical and computational complexity. Our work is mainly inspired by the method of Chui and Rangarajan [25], but performs much faster and requires less memory. Experiments have demonstrated that our method significantly improves the efficiency of registration without decreasing the accuracy of the atlases. Shape variation learned from both femur atlases can be used for clinical studies and diagnosis in the future. Moreover, femur atlases can be used as a statistical prior for shape reconstruction from other imaging modalities such as endoscopy, and also for the segmentation of 3D surfaces from DICOM images.