Surgically oriented measurements for three-dimensional characterization of tunnel placement in anterior cruciate ligament reconstruction

Abstract

Objective: To develop and evaluate the feasibility and reliability of an alternative three-dimensional (3D) measurement system capable of characterizing tunnel position and orientation in ACL reconstructed knees.

Methods: We developed a surgically oriented 3D measurement system for characterizing femoral and tibial drill tunnels from ACL reconstructions. This is accomplished by simulating the positioning of the drill bit originally used to create the tunnels within the bone, which allows for angular and spatial descriptions along defined axes that are established with respect to previously described anatomic landmarks and radiographic views. Computer-generated digital phantoms composed of simplified geometries were used to verify proper calculation of angular and spatial measurements. We also evaluated the inter-observer reliability of the measurements using 10 surfaces generated from cadaveric knees in which ACL tunnels were drilled. The reliability of the measurements was evaluated by intraclass correlation coefficients.

Results: The digital phantom evaluation verified the measurement methods by computing angular and spatial values that matched the known values in all cases. The intraclass correlation coefficient was calculated for four users and was found to range from 0.95 to 0.99 for the femoral and tibial measurements, demonstrating near-perfect agreement.

Conclusions: The characterization of ACL tunnels has historically concentrated on two-dimensional (2D) measurements; however, it can be difficult to define ACL tunnel placement using 2D methods. We have presented novel techniques for defining graft tunnel placement from 3D surface representations of the ACL reconstructed knee. These measurements provide exact tunnel location spatially and along axes that offer the potential to comparatively analyze ACL reconstructions post-operatively using advanced imaging. These methods are reliable, and have been demonstrated to be applicable to multiple single-bundle techniques for ACL reconstruction.

• ACL reconstruction
• 3D measurement
• virtual model
• tunnel angle
• aperture location

Introduction

Disruption of the anterior cruciate ligament (ACL) is a common injury of the human knee, especially in athletes. It has been estimated that nearly 175,000 ACL reconstructions are performed each year, with an estimated cost of up to $1 billion [1–4]. Despite generally good outcomes after ACL surgery, research continues into ways of preventing post-reconstruction problems such as the need for ACL revision reconstruction or the development of osteoarthritis. One of several potential reasons for adverse outcomes following ACL reconstruction is poor tunnel placement [4], [5].

Biomedical researchers have developed image processing and modeling software packages to address various issues in imaging research. In addition to the commercial software options, the BRAINS2 open-source software package is a set of tools used to process and segment three-dimensional (3D) images for the purpose of surface generation and measurement [6]. BRAINS2 was originally designed for brain researchers, but others have used it to validate the accuracy of surface representations of CT images for orthopaedic structures [7]. The manipulation of surface representations for surgical simulations using the National Library of Medicine's open-source Visualization Toolkit (VTK) has also been reported [8], [9]. These open-source tools offer flexibility in addressing a number of imaging-related research questions; here, we have applied them to the evaluation of ACL reconstruction tunnel placement variability.

The characterization of ACL tunnels has largely concentrated on two-dimensional (2D) measurements from standard radiographic views. The European Society of Sports Traumatology Knee Surgery and Arthroscopy (ESSKA) Scientific Workshop on Reconstruction of the Anterior and Posterior Cruciate Ligaments has provided guidelines for describing tunnel locations on the distal femur and proximal tibia [10]. Two-dimensional tunnel evaluation studies using plain films have been performed using these guidelines and variations on them [11–15]. However, it can be difficult to define actual ACL tunnel placement using 2D methods [16]. Previous work has also demonstrated a wide range of inter-rater agreement based on post-ACL radiographs [17].

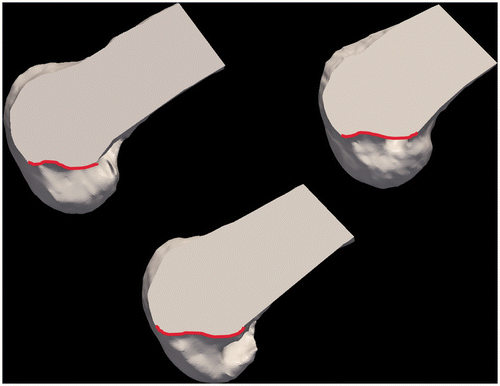
With the advent of CT technologies, several studies have extrapolated the 2D measurements to CT slices [16], [18], [19]. Surface generation from CT images has also been investigated as a method of tunnel placement evaluation [20–24]. Three-dimensional surface-based techniques are desirable due to their ability to visualize not only the bone but also the tunnels through the bone. However, prior systems for evaluating tunnels using CT scans are not readily applied to cadaveric specimens where the malleolar axis is unavailable. In addition, previous tunnel analysis systems [23], [24] have referenced measurements off Blumensaat's line, which the present authors have found to be highly variable and often undulating (Figure 1). Several prior techniques used to analyze the ACL and ACL reconstruction tunnels rely on descriptive anatomical landmarks such as the distance to articular cartilage and small bony ridges, which may or may not be reproducibly evident on advanced imaging after surgery [14], [23], [25].

Figure 1. Three surface representations of cadaveric femurs demonstrating variability in Blumensaat's line (red) when viewed as sagittal sections looking towards the medial wall of the lateral femoral condyle.

The purpose of this study was to create a reproducible ACL tunnel analysis system that allowed 3D characterization of ACL tunnels, and to evaluate the system's feasibility and reliability. Here, we describe our novel methods and evaluate the inter-observer reliability by calculating the intraclass correlation coefficients across multiple raters. We hypothesize that 3D surface representations of the knee and virtual drill bits can be used reliably to characterize ACL tunnel position and orientation in three dimensions for ACL reconstructed knees.

Materials and methods

Three-dimensional measurement system

A three-dimensional measurement system for characterizing femoral and tibial drill tunnels from ACL reconstruction was developed based on commonly used surgical and radiologic landmarks. This includes the usual “notch view” which most surgeons have during arthroscopy when performing ACL reconstruction. During this procedure, the surgeon flexes the knee at approximately 90° and views the notch approximately along the anatomic axis of the femur. Most ACL tunnel radiographic studies have been based on a perfect lateral radiograph, and our measurement technique takes this into consideration as well. Our ability to characterize the drill tunnels relies on simulating the positioning of the drill bit used to create the tunnels within the bone. Based on positioning virtual drill bits within previously generated 3D surface representations of bone, we are able to describe the drill tunnels with angular and proportional spatial measurements. The following sub-sections describe the methods used to develop a standardized 3D orientation, align the bone surfaces to this orientation, generate and align virtual drill bits, match virtual drill bits to drill tunnel apertures, and automatically measure the ACL tunnels spatially and angularly.

Standardized orientation

To ensure accurate and reproducible measurements in three dimensions, a standardized orientation is required for both the femur and the tibia. We have created separate orientations for the femur and tibia based on radiographic and anatomic views. For the femur, the Z-axis is defined by the femoral diaphysis after compensating for 7° of anatomic valgus (Figure 2A). This orientation is established by rotating the femur such that the intermedullary canal is linearly aligned with the Z-axis. The X-axis is defined by a line through the femoral condyles such that the lateral condyle equally overlaps the medial condyle (Figure 2B), which correlates with a perfect lateral 2D radiograph. This orientation is established by rotating the femur relative to the defined Z-axis such that there is perfect overlap of the femoral condyles. The Y-axis is then mathematically defined by the cross-product of the X- and Z-axes.

Figure 2. The standardized orientations of the femur and tibia. For the femur, the Z-axis is aligned with the femoral diaphysis (A) and the X-axis is defined by a line that allows the medial and lateral condyles to be aligned as in a perfect lateral 2D radiograph (B). (The figure demonstrates a femur with modified transparency to allow visualization of the overlap.) For the tibia, the X-axis is aligned with the medial-lateral slope of the tibial plateau (C) and the Z-axis is aligned such that the posterior-most aspects of the medial and lateral condyles of the tibial plateau are linearly aligned (D).

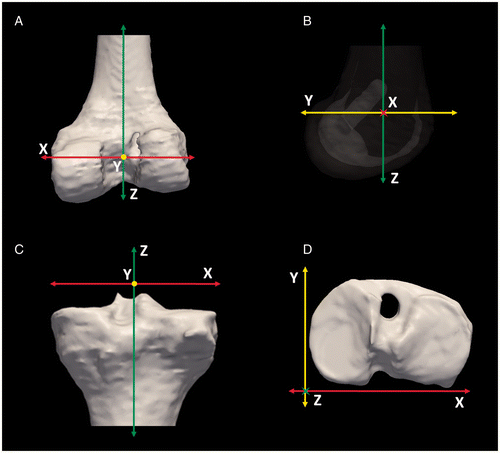
For the tibia, the X-axis is aligned with the medial-lateral slope of the tibial plateau (Figure 2C). This is established by aligning the tibia in an anterior-posterior fashion and then rotating the tibia such that the slope of the tibial plateau from medial to lateral is parallel to the X-axis. The Z-axis is aligned such that the posterior-most aspects of the medial and lateral condyles of the tibial plateau are linearly aligned (Figure 2D). This is accomplished by taking a “bird's-eye view” of the tibial plateau and ensuring that the X-axis is tangent to the posterior-most aspects of the plateau. The Y-axis is then mathematically defined by the cross-product of the X- and Z-axes.

Estimating ACL tunnel position

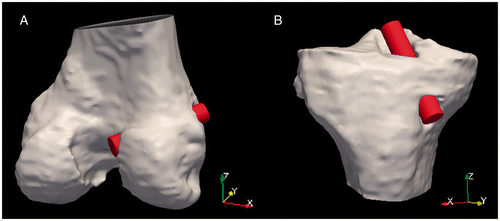
As an estimate of the drill bit used for the surgical procedure, a cylinder was generated with a diameter equivalent to that of the drill bit. For this study, all procedures were performed using a drill bit with a diameter of 10 mm; thus, a virtual drill bit of the same diameter was created. If another size drill bit were to be employed during the procedure, a different virtual drill bit diameter could be used. The cylinder was assigned a length sufficient to adequately traverse the entire length of the drill tunnel; a drill bit length of 50 mm was satisfactory for all specimens used in this study. To compute the position of the tunnel within the bone, the cylinder was placed within the tunnel (Figure 3) using custom tools [8]. Modifying the transparency of the bone surfaces (as demonstrated in Figure 2B) allowed for proper positioning of the virtual drill bits using the entire length of the tunnels to align the bits; this avoided tunnel aperture imperfections and deviations of the central axis of the virtual drill bit caused by fixation hardware. Measurements were based on the central axis of the simulated drill bits.

Figure 3. A cylinder with a diameter of 10 mm was used to simulate the drill bit used to create the ACL tunnels. The cylinders were manually aligned with the tunnels of the femur (A) and tibia (B).

Once the virtual drill bits were aligned with the tunnels, three angles were calculated: α (Equation 1), β (Equation 2), and γ (Equation 3). These angles represent the deviation of the tunnel from the X-, Y- and Z- axes, respectively (Figures 4 and 5).where P₁ is the centerpoint of the endcap of the virtual drill bit closest to the knee joint, P₂ is the centerpoint of the endcap at the opposite end of the drill bit, P_x represents P₁ + 1 unit in the X-direction, Py represents P₁ + 1 unit in the Y-direction, and Pz represents P₁ + 1 unit in the Z-direction.

Figure 4. Tibial tunnel angles (α, β, γ) were measured based on the tunnel centerline's deviation from the surgically oriented coordinate system (A), as demonstrated looking down the Y-axis (B) and the X-axis (C). The points used to calculate the angles are labeled as p1 and p2.

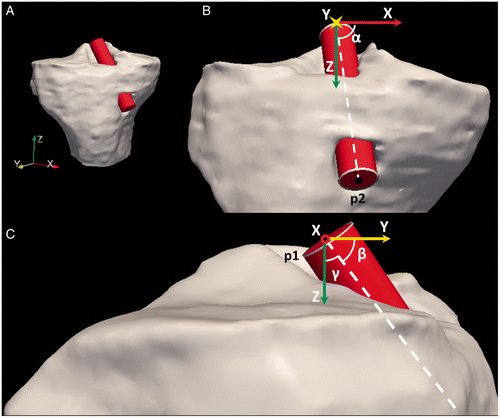
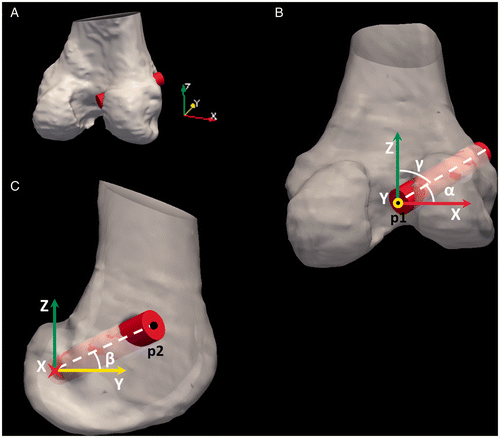
Figure 5. Femoral tunnel angles (α, β, γ) were measured based on the tunnel centerline's deviation from the surgically oriented coordinate system (A), as demonstrated looking down the Y-axis (B) and the X-axis (C). The points used to calculate the angles are labeled as p1 and p2.

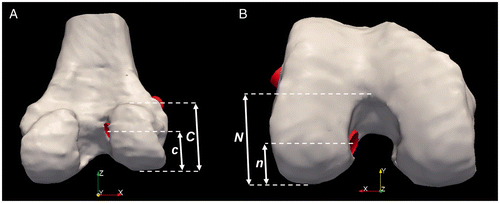
Spatial localization of the ACL drill tunnel apertures allows for correlation of surgical tunnel positioning with respect to proportional measurements of the tibial plateau and the lateral femoral condyle. To estimate the tunnel apertures from the virtual drill bits, the cylindrical surface was cropped at the tunnel aperture using custom software [8]. After the virtual drill bits were cropped to match the tunnel apertures (Figure 6), two spatial measurements for each bone were calculated: m/M and a/A for the tibia and n/N and c/C for the femur. For the tibia, the position of the aperture centerpoint is measured as a proportion of the distance from the anterior aspect of the tibial plateau (a) with respect to the total tibial depth (A), as shown in Figure 7A, and also as a proportion of the distance from the medial aspect of the tibial plateau (m) with respect to the total width of the tibial plateau (M), as shown in Figure 7B. These proportional measurements are readily calculated by evaluating the spatial extents of the bone surface in the standardized tibia orientation previously described.

Figure 6. The virtual drill bits were cropped to match the tunnel aperture on the femur and tibia. Several views are provided, including the posterior aspect of the distal femur (A), a sagittal view of just the lateral femoral condyle (B), and the tibia (C).

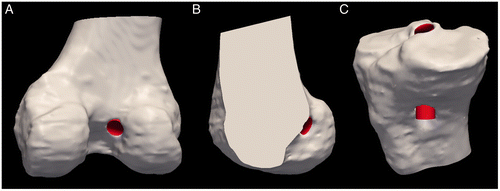
Figure 7. (A) Measurement (a/A) of the tunnel aperture centerpoint based on the anterior-posterior distance of the tibial plateau. (B) Measurement (m/M) of the tunnel aperture centerpoint based on the medial-lateral distance of the tibial plateau.

For the femur, the position of the aperture centerpoint is measured as a proportion of the distance from the distal-most aspect of the lateral condyle (c) with respect to the total diameter of the lateral condyle (C), as shown in Figure 8A, and also as the proportion of the distance from the posterior-most aspect of the lateral condyle (n) with respect to the apex of the intercondylar notch (N), as demonstrated in Figure 8B. Custom tools [8] were used to isolate the lateral femoral condyle in the standardized femur orientation; this readily allowed for the described proportional measurements based on evaluating the spatial extents of the isolated lateral femoral condyle.

Figure 8. (A) Measurement (c/C) of the tunnel aperture centerpoint based on the diameter of the lateral femoral condyle. (B) Measurement (n/N) of the tunnel aperture centerpoint based on the height of the intercondylar notch.

Evaluation using digital phantoms

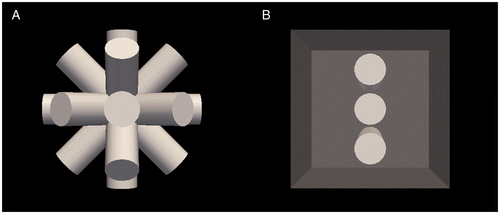
To validate the angular and spatial measurements, two digital phantoms were created. Digital phantoms are computer-generated simplified geometries with known spatial and angular dimensions which are used to ensure proper calculations are performed by software. The angular measurements were validated using nine virtual drill bits in different known orientations (aligned with each major axis and between the major axes), as shown in Figure 9A. The spatial measurements were validated using three virtual drill bits (positioned at 25%, 50%, and 75% of the total cube height) encased in a cube and representing drill tunnels passing through the lateral femoral condyle, as shown in Figure 9B. The resulting calculated angular and spatial measurements were compared to the known values used to generate the digital phantoms, and were found to match the known values in all cases.

Figure 9. (A) A digital phantom including nine virtual drill bits used to test the angular measurements. (B) A second digital phantom including three virtual drill bits encased in a cube, used to test the aperture localization measurements.

Evaluation using cadaveric specimens

Ten cadaveric knee joints were collected (4 left and 6 right); each specimen included the full knee joint and a portion of the proximal tibia and distal femur. Prior to scanning, tunnels for a single-bundle ACL reconstruction were performed by a fellowship-trained orthopaedic surgeon on each specimen, using either the medial portal, transtibial, or two-incision technique. The 10 specimens included four medial portal operations, four transtibial operations, and two two-incision operations by six fellowship-trained orthopaedic surgeons. We considered this sub-sample to be representative of the larger dataset as it included multiple surgeons and three common single-bundle ACL reconstruction techniques. A Siemens Sensation 64-slice CT scanner was used to collect 3D voxel datasets of the knee for each specimen (matrix: 1005 × 512; FOV: 261 mm × 133 mm; KVP: 120; current: 128 mA; exposure: 160 mAs) with a 0.26-mm in-plane resolution and a slice thickness of 0.75 mm. Slices spanning the entire specimen were obtained for each dataset.

The CT datasets were resampled to 1.0-mm isotropic voxels, and all left knees were mirrored along the X-axis to produce 10 right knees for analysis. The BRAINS2 software was used to manually segment the distal femur and proximal tibia [6]. 3DSlicer was used to generate and smooth surface representations from the manual tracings of the 10 femoral surfaces and 10 tibial surfaces.

An average-sized femoral and tibial 3D surface reconstruction were aligned such that the surface orientations corresponded to the standardized orientation described above. The resulting bone reconstructions were verified as matching the desired standardized orientation by an experienced orthopaedic surgeon. The oriented bone surface representation acted as an atlas to which each of the specimens was mapped using an iterative closest point (ICP) rigid registration, a common tool in 3D modeling. The ICP surface registration used 100 iterations and 5000 vertices to align the specimen surfaces without modifying the original bone geometry [26], [27].

Four users – two biomedical engineers and two orthopaedic residents – applied the proposed measurement techniques to evaluate the femoral and tibial ACL tunnels on each of the 10 specimens. Each user was independently trained and performed placement and aperture matching of virtual drill bits in the tibia and femur for the 10 cadaveric datasets on a single occasion. The resulting virtual drill bits were processed using the 3D measurement techniques described above.

Statistical analysis

Standard descriptive statistics were calculated for the angular and spatial measurements for both the femoral and tibial measurements using Microsoft Excel®. The reliability of the raters was evaluated by computing the intraclass correlation coefficients for the described spatial and angular measures using SAS®.

Results

The ten cadaveric specimens showed average and standard deviation values of α = 60 ± 1.2°, β = 50 ± 1.1°, γ = 56 ± 1.0°, n/N = 0.54 ± 0.02, and c/C = 0.68 ± 0.02 for the femur, and α = 78 ± 1.1°, β = 59 ± 1.4°, γ = 34 ± 1.3°, a/A = 0.49 ± 0.02, and m/M = 0.46 ± 0.01 for the tibia. This demonstrates the measurement system's ability to measure three angular and two spatial measurements for each of the ten ACL reconstructed knees. The intraclass correlation coefficient was calculated for the four users and found to range from 0.95 to 0.99 for the femoral and tibial measurements (Table I).

Table I.  Intracorrelation coefficient for 4 trained users for each measurement.

Measurement	Femur	Tibia
α	0.99	0.98
β	0.99	0.99
γ	0.99	0.98
n/N	0.98
c/C	0.98
a/A		0.95
m/M		0.96

Discussion

We have presented a surgically oriented tunnel localization system for ACL reconstructions based on estimating the positioning of surgically generated tunnels for the tibia and femur using surface models. Our measurement guidelines are intentionally designed to be of practical use to the orthopaedic surgeon and provide surgically oriented proportional measurements based on the ESSKA recommendations [10]. By establishing a surgically oriented coordinate system, the aperture spatial measurements and the tunnel angular measurements provide a novel 3D method for describing this inherently three-dimensional procedure.

Our methods are applicable for evaluating surgical procedures that involve the placement of surgical drill bits and bone tunnels such as ACL reconstruction. We have demonstrated their application on single-bundle ACL reconstructions, including the transtibial, medial portal, and two-incision techniques. Simply incorporating a second drill bit would also allow this to serve as a method of evaluation for double-bundle ACL reconstructions. In addition, the method could be used to evaluate PCL reconstruction and other procedures involving bone tunnels for graft placement. The methods are reliable, with intraclass correlation coefficients ranging from 0.95 to 0.99 among four users with both surgical and nonsurgical backgrounds. These high values can be attributed to a small degree of variability between raters in placing the virtual drill bits and a high degree of variability in the tunnel angles themselves. Intraclass correlation coefficients investigating intra-observer variability were considered unnecessary due to the excellent inter-observer correlation coefficients.

Blumensaat's line has traditionally been a radiographic landmark important in describing the placement of ACL tunnels in two dimensions. Recently, Forsythe et al. [23] and Kopf et al. [24] have demonstrated the use of 3D surfaces to characterize tunnel locations using quadrants and spatial dimensions based on Blumensaat's line; however, we found this landmark difficult to define reliably in a large set of knee specimens because of significant anatomical variation and undulation of Blumensaat's line on 3D surfaces. Hence, this induced variability in the measurements, since determining the starting point was difficult. We therefore provide an alternative measurement tool based on standardized bone orientations.

Our surgically oriented coordinate system does deviate from orientations that have been proposed in the past. With respect to the femur, Grood and Suntay [28] proposed orienting the Z-axis so that it corresponded to the femoral mechanical axis (partially defined with the femoral head). With respect to the tibia, they proposed aligning the Z-axis with the tibial mechanical axis (partially defined with the tibial malleoli). Forsythe et al. [23] and Kopf et al. [24] based their coordinate system on the recommendations of the International Society of Biomechanics and Grood and Suntay [28]. During ACL reconstructions, the femoral head is typically draped and is difficult to reference intraoperatively. In our measurement system, we have aligned the diaphysis of the femur with the Z-axis; this allows measurements to be taken with respect to a portion of the femur directly visible during the procedure. Our X- and Y- axes are defined similarly to those described by Grood and Suntay [28]. For the tibia, instead of orienting with respect to the tibial malleoli, we have oriented the tibia with regards to surface features of the tibial plateau. Overall, our orientations were defined by aligning the femur and tibia with landmarks that are visible during the operative procedure, which is also helpful in cadaveric studies where the entire limb is not available.

Current limitations and areas for future work revolve around manual procedures in our methodology, including manual segmentation of the images and manual placement of virtual drill bits for the measurements. Future improvements to our methods will include fully automated surface generation of the tibia and femur [29], and automated placement of the virtual drill bits into the drill tunnels to foster an automated measurement system. With these improvements, this tool could be used for surgical planning, where the optimal position of the tunnel would be identified automatically.

In current practice, MRI images are typically obtained in ACL reconstruction cases requiring revision. In our pilot study, we have used surfaces generated from CT images with 1.0-mm isotropic voxels, which could be seen as a limitation of our study's clinical applicability. Future applications of our methodology to MRI images will bring our methods closer to clinical usefulness. In addition, clinical studies will also include surgical hardware used in the ACL reconstruction, which can lead to beam hardening artifacts in images. These artifacts can affect image quality depending on the type of hardware configuration chosen by the surgeon. Our study did not include subjects with hardware; however, previous studies have demonstrated that the presence of hardware can actually be helpful in identifying ACL tunnels in postoperative images [17]. Based on our experience with clinical images including hardware, we do not foresee hardware interfering with our methodology of ACL tunnel measurement.

As previously mentioned, our methods offer a number of advantages by avoiding measurements on Blumensaat's line and by using surgical landmarks that are visible during the procedure; however, results obtained using our measurement system can be difficult to compare directly to previous work due to the differences in methodology. In the future, we hope to develop an estimated mathematical conversion between our methods and previous approaches to allow for comparison to prior research.

From a research perspective, this is the first tool to allow for a 3D measurement of both angular and spatial dimensions in ACL reconstruction. The techniques presented in this study were developed to evaluate 150 ACL reconstructions performed by the MOON Knee Group to investigate ACL tunnel variability. This analysis will help to establish mean and extreme values encountered in ACL tunnel placement and in multi-surgeon cohort studies. With angular and spatial localization data, this work will also potentially allow future finite element investigations to be performed on ACL reconstructed knees to optimize tunnel position and orientation. Clinically, we hope a future version of this tool will allow individual surgeons to evaluate ACL tunnel placement in cases of reconstruction failure, thereby identifying technical failures and improving their practice, or to help plan revision surgery.

Conclusions

We have presented a surgically oriented three-dimensional method for evaluating tunnel placement/orientation for ACL reconstructions. These methods are reliable, with intraclass correlation coefficients ranging from 0.95 to 0.99. We have also demonstrated the methods to be applicable to multiple single-bundle techniques of ACL reconstruction.

Acknowledgments

The authors would like to acknowledge DonJoy Orthopaedics (Carlsbad, CA) for providing the cadaveric specimens and the Multicenter Orthopaedic Outcomes Network (MOON) Knee Group, based at Vanderbilt University, including Drs. Andrish, Amendola, Brophy, Carey, Cox, Dunn, Flanigan, Jones, Kaeding, Marx, Matava, McCarty, Parker, Spindler, Vidal, Wolcott and Wright, for providing the CT scans/surgery.

Declaration of interest: The authors report no declarations of interest.