Towards modeling tumor motion in the deflated lung for minimally invasive ablative procedures

Abstract

A computational model is proposed to demonstrate the feasibility of characterizing the motion of lung tumors caused by respiratory diaphragm forces using a tissue biomechanics approach. Compensating for such motion is very important for developing effective systems of minimally invasive tumor ablative procedures, e.g., Low Dose Rate (LDR) lung brachytherapy. To minimize the effects of respiratory motion, the target lung is almost completely deflated before starting such procedures. However, a significant amount of motion persists in the target lung due to the diaphragm contact forces required for the other lung's respiration. In this study, a model pipeline was developed which inputs a pre-operative 4D-CT image sequence of the lung to output the predicted 3D motion trajectory of the tumor over the respiratory cycle. A finite element method was used in this pipeline to model the lung tissue deformation in order to predict the tumor motion. Experiments were conducted on an ex vivo porcine lung to demonstrate the performance and assess the accuracy of the proposed pipeline. The resultant tumor motion trajectory obtained from the biomechanical model of the lung was compared to the experimental trajectory obtained from CT imaging. Results were promising, suggesting that tissue mechanics-based modeling can be employed for effective characterization of lung tumor respiratory motion to improve accuracy in lung tumor ablative procedures.

• Lung brachytherapy
• tissue deformation
• tumor motion
• diaphragm forces
• FEM

Introduction

According to the American Cancer Society, lung cancer is one of the most prevalent forms of cancer, with an estimated 226,160 new cases in the United States during 2012 [1]. Moreover, due to the difficulties frequently associated with treating lung cancer, it continues to be the principle cause of cancer death in both men and women. Current methods for lung cancer treatment, including surgery, chemotherapy, and external radiation therapy, suffer from high morbidity and mortality rates in addition to causing several side effects.

While surgical resection of cancerous tissue through a full lobectomy is the treatment of choice, this is very invasive and not suitable for older patients or those with weak pulmonary systems. Chemotherapy also involves various long-term side effects. Sub-lobar (wedge) resection is another alternative approach which has been attempted in order to address the limitations of the full lobectomy procedure in patients with poor physiologic reserve or those of advanced age. However, wedge resection was found to be associated with an increased incidence of post-operative local recurrence [2], [3]. This disadvantage has subsequently been diminished, to some extent, by applying intra-operative LDR brachytherapy as an adjuvant treatment [4–6]. Intra-operative LDR brachytherapy is accomplished by placing radioactive seeds sewn in a mesh on the resection margin of the lung. The mesh is then stapled and permanently secured by the thoracic surgeon. While this supplemental therapy may effectively address the local recurrence associated with wedge resection [4], [5], it still requires surgical resection, potentially leading to higher morbidity rates in comparison to minimally invasive techniques.

Minimally invasive LDR brachytherapy is a new method that has recently been proposed as a primary treatment for lung cancer. This method involves internal slow irradiation of malignant tumors by small radioactive seeds which are permanently implanted in the tumor using rigid hollow needles [7], [8]. Application of minimally invasive LDR brachytherapy in targeting lung cancer is expected to result in lower morbidity and mortality rates, as well as fewer side effects.

A successful outcome of a brachytherapy procedure is contingent upon accurate placement of the radioactive seeds consistent with a distribution pattern determined pre-operatively by medical physicists. The seed distribution pattern is arranged on the basis of radiation dosimetry, where sufficient radiation is delivered to destroy cancerous cells while the surrounding normal tissue receives only a minimal dose of radiation such that it is not damaged. Even small deviations from the pre-planned distribution pattern may result in a considerable volume of tissue receiving an excessive or insufficient radiation dose [9], thus impacting the success of the procedure. LDR brachytherapy has been applied clinically for treating brain [10] and prostate [11] cancers; however, to adapt this minimally invasive concept for targeting lung cancer, a number of challenges must be overcome. These challenges pose serious obstacles for achieving the pre-planned distribution pattern of radioactive seeds throughout the operation. They include uncertainties about the exact physical location of the tumor during seed implantation, as this varies throughout the procedure due to the complex motion of the tumor. A major source of tumor motion in LDR lung brachytherapy procedures is respiratory contact forces between the diaphragm and lung. While this motion is minimized by deflating the target lung almost completely before commencing the operation, it remains a significant factor as the diaphragm continues its motion to facilitate respiration with the other lung.

This paper describes a practical framework for tracking lung tumor motion in LDR lung brachytherapy where the lung is deflated. Within this framework, the main focus is a lung biomechanical model capable of predicting the tumor motion resulting from interaction between the lung and diaphragm. This model which has been developed based on a Finite Element Method (FEM) formulation. FEM, or alternatively, the recently developed accelerated Statistical FEM (SFEM) [12], has been shown to provide high accuracy in many biomedical applications [13–16], including thoracic surgery planning and guidance [17], [18]. Al-Mayah et al. used FEM to investigate the effect of contact surfaces, friction, and material compressibility, as well as hyperelastic material properties, on the mechanical behavior of human lungs [19–21]. They used tetrahedral elements for meshing the lung geometry, and also employed the biaxial tension test data reported by Zeng et al. [22] to fit a strain energy model in their lung hyperelastic model. While the results reported in references [19–21] provide a good foundation for biomechanical analysis of the lung in cancer treatment procedures, using tetrahedral elements to mesh the lung geometry is known to suffer from several issues, including locking and analysis convergence, especially with incompressible materials. Moreover, the biaxial tension test data used in the aforementioned work was obtained using old measurement instruments that lacked high precision, while the test data analysis involved significant sample geometry and boundary condition uncertainties. Due to the lack of other sources of lung tissue hyperelasticity data, Eom et al. also used the same biaxial tension dataset in their recently presented lung biomechanical model [23]. They employed FEM to develop a respiratory motion model for predicting lung tumor motion over a complete normal breathing cycle. According to their results, FEM exhibited favorable performance for respiration-induced tumor motion. It should be noted, however, that the above research efforts investigated the use of biomechanical models of the breathing lung to determine the lung tissue deformation throughout the respiration cycle. To the authors’ knowledge, no biomechanical model has yet been proposed for predicting tissue deformation of a deflated lung under diaphragm contact forces during respiration of the other lung.

The main purpose of this paper is to present a biomechanical modeling pipeline to demonstrate the feasibility of predicting respiratory tumor motion due to diaphragm forces in tumor ablative procedures. The development of this pipeline is complementary to our research efforts directed towards developing an image guided minimally invasive LDR lung brachytherapy system [24–28]. As described in the next section, the pipeline involves a lung biomechanics model formulated via an FEM framework employed to calculate the respiratory tissue motion and deformation. The outcome of FEM analysis can be used to estimate the 3D trajectory of the tumor and to present it as a function of diaphragm location at each phase of respiration. It is noteworthy that the diaphragm contact motion can be predicted based on optical/electromagnetic tracking data through the method presented by Vedam et al. [29], or characterized in real-time fashion using the approach proposed by Zhao et al. [30]. This facilitates real-time prediction of tumor location, which is an essential prerequisite for successful lung tumor ablative procedures.

Ex vivo experiments were conducted to evaluate the performance of the proposed pipeline and demonstrate its potential efficacy in lung tumor ablative procedures. The results obtained confirmed the accuracy of the pipeline for characterizing the 3D trajectory of the tumor in the proposed applications. The pipeline thus represents a critical step towards fully developing a high-precision system for lung tumor ablative procedures. While favorable performance was observed in the ex vivo experiment, providing a proof of principle, in vivo studies are required to further evaluate the pipeline and fine-tune its parameters for clinical applications.

Materials and methods

Figure 1 presents a schematic diagram for a minimally invasive LDR lung brachytherapy concept based on the pipeline proposed in this study, which provides a practical framework for the concept. Elements of the diagram that fall within the scope of this investigation, with an emphasis on the lung FE model, are described below. While the description is applicable to tumor motion tracking in clinical LDR lung brachytherapy, an experiment involving an ex vivo porcine lung containing a gelatine-agar tumor phantom was conducted to assess the performance and accuracy of the proposed tumor motion tracking technique and provide a proof of concept.

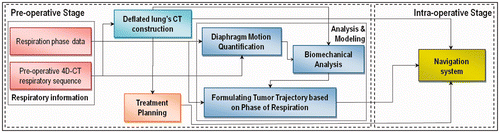
Figure 1. Schematic diagram of the proposed image guided minimally invasive system for lung tumor ablative procedures. Pre-operative steps start with acquiring a 4D-CT respiratory sequence along with its corresponding respiration phase data. The 4D-CT sequence is used to construct a CT image of the deflated lung. In conjunction with the respiration phase data, the sequence is also used to quantify the respiratory diaphragm motion. The constructed CT image is initially used for pre-operative treatment planning. It is also used, along with the quantified diaphragm motion, for biomechanical analysis of the lung's respiratory tissue motion and deformation. The resulting tumor motion is then formulated as a function of the respiration phase data. In the intra-operative phase, respiration phase data is acquired using tracked fiducial marker data, and the tumor motion is estimated using the relationships obtained from the proposed model pre-operatively. The estimated tumor motion, along with the constructed CT image of the deflated lung and the treatment plan, can be used as input in the surgical navigation system for accurate operative guidance.

Lung FE model

The proposed pipeline uses a lung biomechanical FE model to predict tumor motion. There are several prerequisites for constructing an FE model capable of accurate tumor motion characterization during an LDR brachytherapy procedure, including availability of tissue biomechanical properties, and modeling and image processing techniques. As mentioned previously, methods have recently been developed to fulfill a number of these prerequisites, as described below.

Deflated lung geometry calculation and FE meshing

To create an FE mesh of a lung in this brachytherapy application, the geometry of the deflated lung is required. The lung geometry must also be simplified systematically to reduce the model's computational complexity without compromising its accuracy. In the proposed pipeline, the geometry was extracted from a high-quality CT image of the totally deflated lung, constructed using a technique described in reference [26]. This technique inputs the patient's 4D-CT respiratory image sequence acquired pre-operatively to construct the corresponding deflated lung's CT image. It consists of a deformable registration/air volume estimation/extrapolation pipeline. The essence of this technique is finding the deformation field between the image of the most respired lung and the image of the lung at each respiration phase as a function of the lung's air volume at each phase. Once such a function is determined based on the pre-operative 4D-CT images of the lung, the deformation field can be obtained by extrapolation techniques for the totally deflated lung at air volume ∼0. This deformation field can then be combined with the image of the most respired lung to obtain the image of the totally deflated lung. The technique does not require any external markers to find the image deformation function, as the function is given in terms of the air volume inside the lung. This volume at each phase was calculated automatically from the lung CT images using a thresholding segmentation technique described elsewhere [25].

To avoid incorporating anatomical details that have no significant impact on the accurate estimation of tumor motion, the extrapolated geometry of the deflated lung was simplified by omitting insignificant airways and blood vessels according to the criteria established in reference [28]. The simplified geometry was subsequently used to develop a 3D surface of the lung. For FE meshing, the constructed image of the deflated lung was first segmented using 3D Slicer open-source software, wherein a thresholding algorithm was used [31]. Using the output of this segmentation, a Gaussian filter implemented in 3D Slicer was applied to create and smooth the lung surface model, which is necessary to create an FE mesh. An accurate FE mesh was then created from the resulting smooth surface. This was achieved using the IA-FEMesh open-source software [32] with an elliptical interpolation and 8-node hexahedral elements. This software uses the Transfinite Interpolation (TFI) concept described in reference [33] to generate high-quality hexahedral elements known for their efficiency, desirable accuracy, and convergence properties. The generated FE mesh has 25,610 nodes and 22,350 8-noded hexahedral elements.

Lung tissue biomechanical properties

Lung tissue, similar to most biological soft tissues, is hyperelastic, as it exhibits intrinsic nonlinear biomechanical behavior [34], and is expected to undergo finite deformation during LDR brachytherapy procedures. However, reliable hyperelastic parameters of lung tissue are rare. In this study, we incorporated lung tissue hyperelastic parameters measured recently using indentation tests followed by an inverse FE solution [27]. The deflated lung tissue was considered incompressible in this work, and its intrinsic biomechanical behavior was characterized using a Yeoh strain energy model with parameter values measured at C₁₀ = 194.4 Pa, C₂₀ = 257.9 Pa and C₃₀ = 0.0033 Pa. The gelatin-agar tumor phantom was assumed to be linearly elastic with a Young's modulus value being measured using a uniaxial test at 18 KPa.

Lung FE model prescribed boundary conditions

Determining the lung FE model boundary conditions requires modeling the intra-operative lung-diaphragm mechanical interaction. During respiration, the lung is mechanically loaded by forces exerted by the diaphragm. In the proposed lung FE model, this loading is simulated using prescribed displacement boundary conditions that model the interaction between the lung and the diaphragm. Delineation of the displacement data of the boundary conditions requires knowledge of the position and configuration of the upper surface of the diaphragm at each respiration phase. The position and configuration of this surface can be obtained by delineating the diaphragm's superior surface in contact with the lung from each 3D volume of the thoracic 4D-CT respiratory image sequence obtained pre-operatively via segmentation. The prescribed displacement boundary conditions can be estimated for each respiration phase by calculating the distance distribution between the segmented surfaces of the current phase and the inhalation phase. The boundary conditions at each time point during the respiration cycle (t_in ≤ t ≤ t_ex, where t_in and t_ex are the inhalation [t = 0] and exhalation times, respectively) can be obtained by interpolation. To determine t, which is necessary to estimate the boundary conditions intra-operatively, quantitative spirometry parameters, tracking data for extrinsic/intrinsic markers, or a hybrid data structure may be used [29], [30]. Of these, the extrinsic marker tracking approach can be used effectively by pre-operatively placing on the chest a small set of fiducial markers that are visible on a thoracic CT scan and recording their positions as a function of time. The positions of the markers are correlated with the respiration phase. A function can therefore easily be developed using a curve fitting approach based on the pre-operatively acquired data. This function can be used intra-operatively by inputting the marker positions tracked by an optical/electromagnetic tracking system to output the time t needed to determine the prescribed displacement boundary conditions.

The lung FE mesh, in conjunction with its tissue hyperelastic parameters, the Young's modulus of the tumor given earlier, and the boundary conditions, was input into the FEM block. This block was developed using the ABAQUS software package (Simulia, Dassault Systèmes Corp., RI). In this model, C3D8H hybrid elements were used to account for tissue incompressibility of the deflated lung. Also, consistent with the tissue hyperelastic model, geometric nonlinearity was considered. The biomechanical model, in conjunction with a quasi-static loading scheme, was analyzed and solved in this block to obtain the lung tissue 3D displacement field. The 3D trajectory of the tumor was then extracted from this field. This trajectory is presented as a function of the respiration phase. The latter can be applied intra-operatively to track and compensate for the tumor's motion in a surgical navigation system by inputting the respiration phase obtained from the intra-operative fiducial marker data, as described earlier.

Ex vivo porcine lung experiment

Ex vivo experiments were conducted on a porcine lung to evaluate the performance and accuracy of the proposed technique. A phantom tumor was constructed from gelatin and agar in addition to ∼3 mg/ml iodine CT contrast agent, such that it had an HU of ∼200. The phantom tumor was sutured inside a porcine left lung, which was then respired continuously using an intra-tracheal tube in conjunction with a ventilator machine. A 4D-CT respiratory sequence was then acquired while the lung was being respired continuously. The scans were obtained using a GE Healthcare Discovery CT 750 HD scanner. A series of 4.0-cm axial field-of-view sequential adjacent cine scans were performed. The CT scanning parameters were as follows: 80 kVp, 200 mA, and a gantry rotation period of 0.4 s. The 4D-CT images were produced using the 4D-CT sorting method described by Carnes et al. [35]. The acquired 4D-CT image sequence was used to construct a CT image of the lung in its totally deflated mode using the approach described earlier. Afterwards, the lung was completely deflated by applying a negative pressure via the bronchi, and subjected to a set of experiments to study the effects of diaphragm contact forces.

To simulate the respiratory loading of the diaphragm, the inferior surface of the deflated lung was placed on the curved wall of a glass beaker with a diameter of 11 cm, while the lung was suspended above the beaker by fixing the trachea to a solid frame. To assess the proposed tumor tracking technique, qualitative validation followed by quantitative validation was conducted. For the qualitative validation, a small circular area adjacent to the embedded tumor was marked on the surface of the lung before loading to facilitate visual tracking. For the quantitative validation, lung CT images were acquired at different stages while the lung was being loaded by the beaker. To initiate the loading, the beaker was moved up slowly, raising its undersurface by means of a simple crank mechanism until it barely touched the inferior surface of the lung. Then, to mimic real respiratory diaphragm function, the beaker was incrementally raised up to 25 mm in the Z (S-I) direction [36] while the elevation was being measured using a digital caliper. The loading was modeled using a contact mechanics formulation incorporated into the FE model [37]. This formulation follows a master-slave scheme, wherein the rigid beaker surface is considered to be the master while the inferior surface of the lung is considered to be the slave. The formulation ensures that the lung tissue deformation occurs consistent with the beaker's surface geometry, in addition to satisfying the equilibrium equations. This contact loading formulation requires the amount of beaker surface displacement as a prescribed boundary condition. The numerical solution to this contact problem follows an incremental scheme, whereby the prescribed displacement boundary condition is applied incrementally, followed by estimation of the contact surface and displacement field. For qualitative validation of the proposed tumor motion tracking technique, images of the lung were also acquired in the undeformed and deformed states.

Results

Figure 2 shows one CT image slice of the experimentally deflated porcine lung. The figure also shows the corresponding CT image slice obtained from the constructed CT image volume. Quantitative evaluations performed on the tumor center and its boundaries, as well as on a number of anatomical features, confirmed a sub-millimetric accuracy for the constructed CT image, with maximum and average absolute position errors of (0.96, 0.43, 0.29) and (0.71, 0.32, 0.17) mm, respectively. Figure 3 shows the actual deflated lung before and after applying the contact forces, with the circular area marked on the surface. Visual tracking of this area's motion indicated qualitative agreement with the 3D tumor motion trajectory predicted by the lung biomechanical model, as illustrated later. Figure 4 shows a tumor-containing slice of a CT image sequence of the deflated lung during the experiment. It includes four images of the same tumor slice tracked at four phases of the progressive beaker loading applied to the deflated lung. The tumor is visible with high contrast, showing its variable position in the S-I direction. Using the developed contact FE model, Figure 5 was produced, showing a sequence of the lung's displacement field obtained through a corresponding sequence of simulated respiration.

Figure 2. Result of the CT image construction. (a) Acquired CT image of the totally deflated lung for the purpose of validation. (b) Constructed CT image of the totally deflated lung. Quantitative evaluations performed on the tumor center and its boundaries, as well as on a number of anatomical features (a few of which are indicated by arrows), confirmed a sub-millimetric accuracy for the constructed CT image.

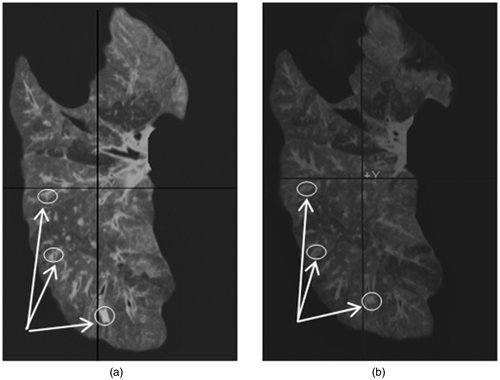
Figure 3. Ex vivo experiment conducted for model validation. The projection of the tumor area inside the lung has been tagged on the surface (a) under minimum contact and (b) after displacing the contact surface by 25 mm in the Z direction.

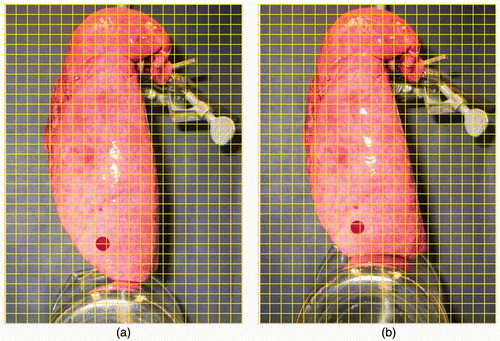
Figure 4. CT image sequence corresponding to the progressive loading applied to the deflated lung. The tumor slice in each image is outlined by a red circle. The same tumor slice has been tracked and shown throughout the CT image sequence.

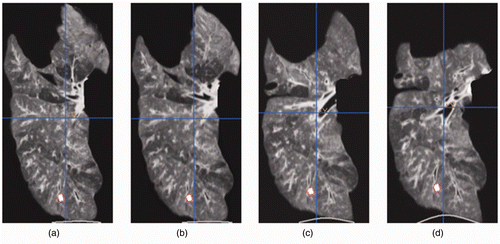
Figure 5. Results of FE simulation. The projection of the tumor area inside the lung is highlighted on the surface. The panels show the undeformed lung (a) together with three samples from the lung deformation field sequence (b–d) for a complete phase of simulated respiration.

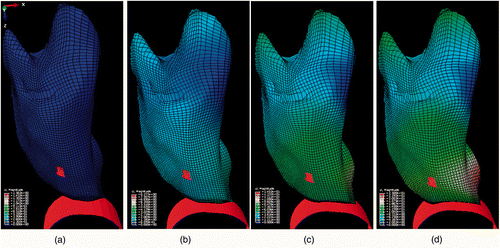
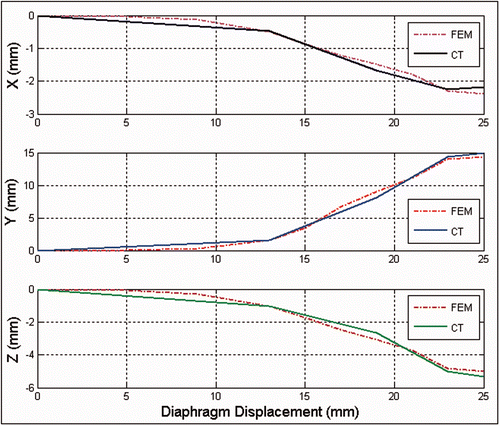
For quantitative validation, accuracy assessments were carried out on the displacement results obtained for a number of traceable anatomical features in both the experimental CT image sequence and the corresponding image sequence obtained by the FE simulation (Figures 4 and 5). Such anatomical features included the tumor center as well as tumor and soft tissue boundaries. This assessment yielded an average error of (0.73, 1.41, 0.99) mm, which indicates that the results of the ex vivo experiment and the lung biomechanical model match quite well. To assess the accuracy of the tumor motion trajectory obtained with the proposed model, the experimental 3D trajectory of the tumor as a function of the diaphragm motion was first extracted from this CT image sequence. To obtain this trajectory function from the CT image sequence, the displacements of the tumor center and the beaker contact surface were calculated using each pair of successive images throughout the CT sequence. This provided a set of corresponding (tumor, beaker) displacement points for the entire sequence to be compared with the simulated trajectory function. Next, the 3D trajectory of the tumor was obtained from the lung FE biomechanical model solution and presented as a function of the beaker motion. By superimposing the former experimental and simulation results, the graphs shown in Figure 6 were obtained. These illustrate the motion trajectories in each direction obtained from the ex vivo experiments, along with those acquired from the FE simulation. As can be seen in the graphs, while the contact surface was mainly displaced in the Z direction, the tumor motion was translated by a considerable amount in all three directions due to soft tissue volumetric deformation. This confirms our observation in the lung surface visual assessment used for qualitative validation. Moreover, the quantitative evaluation comparing the 3D trajectories obtained from the CT image sequence of the contact displacement with those obtained from the FE simulation confirmed a highly accurate coincidence. The average and maximum absolute errors between the two trajectories in the x, y and z motion directions were calculated at (0.27, 0.86, 0.46) mm and (0.49, 1.23, 0.67) mm, respectively.

Figure 6. Graphs showing the 3D tumor trajectory due to lung tissue motion and deformation obtained from the CT sequence in the ex vivo experiment (solid line), as well as that acquired from FE simulation via the proposed pipeline (dashed line).

Discussion

In this paper, a pipeline has been proposed for modeling tumor motion in a deflated lung due to respiratory contact forces. Compensation for this motion is necessary in minimally invasive tumor ablative procedures. The pipeline was introduced as a significant incremental step towards achieving accurate seed placement in LDR lung brachytherapy system development. Another potential application for the proposed technique is the development of virtual reality systems [38], [39] which can be used to train thoracic surgery residents. The main emphasis of the pipeline is the development of a lung FE model capable of predicting the tumor motion as a function of the respiration phase. This began with using an image registration-extrapolation technique to construct the image of the deflated lung from its corresponding pre-operative CT image sequence. This image was then used to construct a smooth 3D surface of the lung. The surface was meshed with 8-noded hexahedral elements, which are known to have desirable performance characterized by accuracy, modest memory requirements and computation time, as well as good convergence properties. The lung tissue properties were characterized with reliable hyperelastic parameters measured recently.

During LDR lung brachytherapy, the deflated lung is loaded by the moving diaphragm throughout respiration of the other lung. This loading was modeled as a prescribed displacement boundary condition. These prescribed boundary conditions can be extracted by segmenting the diaphragm's superior surface and measuring the distance between consecutive segmented surfaces in the S-I direction. The constructed FE model was used to calculate the lung tissue displacement field. The sequence of the displacement fields during respiration was used to formulate the 3D trajectory of the tumor as a function of its motion versus respiration phase. This phase can be determined intra-operatively for tumor motion estimation by tracking the motion of fiducial markers as described in the Methods section. It should be noted that all image processing and FE modeling and analysis steps need to be performed offline. For greater efficiency, the offline FE analysis may be accelerated using the recently developed Statistical Finite Element Method [12] or by employing a GPU-based FEM solver [40].

Ex vivo experiments were conducted to provide a proof of principle for the proposed technique, and to evaluate the pipeline's performance and precision. Evaluation of the results obtained confirmed that the accuracy of the pipeline was reasonable for its proposed application, as the maximum error was a little over 1 mm. This pipeline thus represents a critical step forward for our and other groups’ ongoing development of a high-precision system for lung tumor ablative procedures. In vivo experiments are required to fine-tune the pipeline parameters and ensure its reliability and rigor for clinical applications. Comparing the results obtained in this study with those reported by Eom et al. [23] for modeling motion of the respiring lung over the entire respiratory cycle (maximum position error = ∼5.8 mm; average position error = ∼3.5 mm) indicates that our results are encouraging. Errors obtained in this investigation include error components from the image processing, experimental procedure and FE modeling of the pipeline. The results reported by Eom et al [23] were obtained from in vivo studies of an active (not deflated) lung. Considering the more accurate lung tissue hyperelastic parameters, in addition to the C3D8H hybrid elements, used in this research, the proposed pipeline for modeling tumor motion in the deflated lung is expected to achieve similar results in the in vivo experiments planned for the future.

Declaration of interest: This research was supported by the Natural Sciences and Engineering Research Council (NSERC) of Canada and the University of Western Ontario.