A graphical method for determining inhibition constants

Abstract

A new simple graphical method is described for the determination of inhibition type and inhibition constants of an enzyme reaction without any replot. The method consists of plotting experimental data as (V–v)/v versus the inhibitor concentration at two or more concentrations of substrate, where V and v represent the maximal velocity and the velocity in the absence and presence of inhibitor with given concentrations of the substrate, respectively. Competitive inhibition gives straight lines that converge on the abscissa at a point where [I] = −K_i. Uncompetitive inhibition gives parallel lines with the slope of 1/K’_i. For mixed type inhibition, the intersection in the plot is given by [I] = −K_i and (V–v)/v = −K_i/K’_i in the third quadrant, and in the special case where K_i = K’_i (noncompetitive inhibition) the intersections occur at the point where [I] = −K_i and (V–v)/v = −1. The present method, the “quotient velocity plot,” provides a simple way of determining the inhibition constants of all types of inhibitors.

Keywords::

• Graphical analysis
• inhibition
• inhibition constants
• quotient velocity plot

Introduction

It has long been common practice to determine the inhibition constants of competitive and noncompetitive inhibitors by use of Dixon plots^[1], in which the reciprocal velocity, 1/v, is plotted against the inhibitor concentration, at two or more values of the substrate concentration. Noncompetitive inhibition gives straight lines converging on the abscissa at –K_i at different concentrations of the substrate, whereas in competitive inhibition extrapolated lines at different substrate concentrations intersect at a single point in the fourth quadrant; this point gives –K_i values. However, the usefulness of the Dixon plot is limited by the fact that it cannot be applied to uncompetitive inhibition^[2]. Cornish-Bowden presented an improved method for the determination of K’_i in uncompetitive inhibition, but this plot itself cannot provide the inhibition constant for competitive inhibition^[3]. At present, the inhibition constant can be determined by concomitant use of the Dixon plot and the Cornish-Bowden method. This article presents the “quotient velocity plot,” a new graphical method for direct determination of the inhibition type and inhibition constants including competitive, noncompetitive, and uncompetitive inhibition.

Theory and model

We may write the following reaction scheme

1

It is formally convenient to regard K_m, K9_m, K_i, and K9_i as dissociation constants of the enzyme–inhibitor complexes as described in Equation (1). General inhibition types are described by the rate equation:

2

in which V is the maximal velocity. From the rate equation, it follows that:

2

Types of inhibition

Competitive inhibition

In competitive inhibition, binding of the substrate and the inhibitor to the enzyme is mutually exclusive; thus, K’_i = ∞ and K’_m = 0. We have the following equation for competitive inhibition:

3

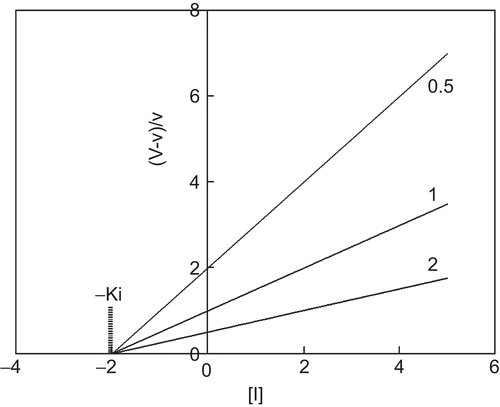
The relationship between (V – v)/v and [I], the concentration of the inhibitor, gives straight lines converging on the abscissa at –K_i at different concentrations of the substrate (Figure 1).

Figure 1.  Quotient velocity plot for competitive inhibition. The lines were drawn in accordance with Equation (3). The following values of parameters were used: K_m = 1 and K_i = 2. The substrate concentration is indicated by each line.

Noncompetitive inhibition

In noncompetitive inhibition, both the substrate and the inhibitor bind to the enzyme at completely independent sites, and the affinity of the substrate (inhibitor) is unaffected by the inhibitor (substrate): K_m = K’_m and K_i = K’_i. We have the following equation for noncompetitive inhibition:

4

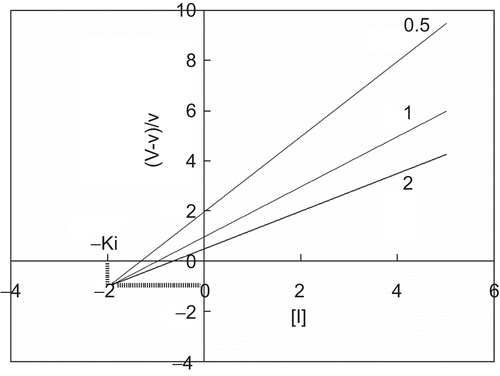
Equation (4) converts a series of inhibition curves obtained with different substrate concentrations into a single straight line converging in the third quadrant at −K_i and −1 (Figure 2).

Figure 2.  Quotient velocity plot for noncompetitive inhibition. The lines were drawn in accordance with Equation (4). The following values of parameters were used: K_m = K’_m = 1 and K_i = K’_i = 2. The substrate concentration is indicated by each line.

Uncompetitive inhibition

Uncompetitive inhibitor does not combine with the free enzyme, but only with the ES complex: K_i = ∞ and then K’_m = 0. Equation (2) can be rearranged into the following form:

5

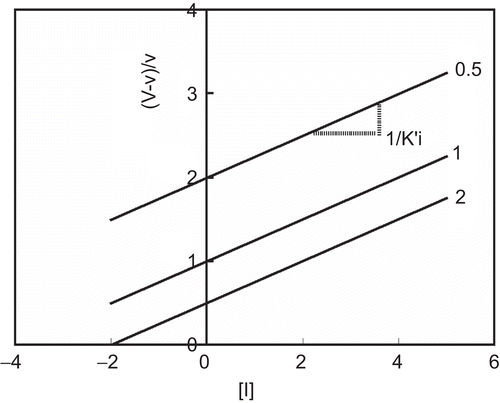
When different substrate concentrations are used, a relationship of (V – v)/v with [I] shows parallel straight lines with a slope of 1/K’_i (Figure 3).

Figure 3.  Quotient velocity plot for uncompetitive inhibition. The lines were drawn in accordance with Equation (5). The following values of parameters were used: K_m = 1, K’_i = 4, K’_m = 0, and K_i = ∞. The substrate concentration is indicated by each line.

Mixed type inhibition

General Equation (2) can be applied to mixed type inhibition, and we rearrange this equation as follows:

6

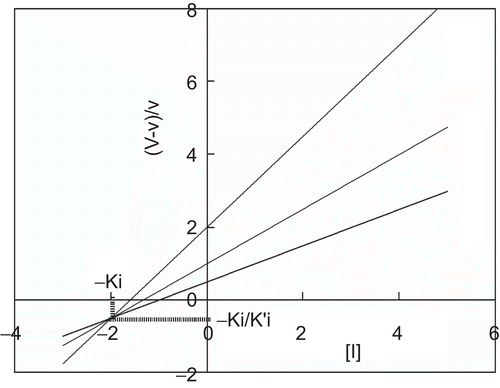
A relationship of (V – v)/v with [I] shows a straight line converging at –K_i and –K_i/K’_i in the third quadrant. We can calculate the K’_i value from this point (Figure 4).

Figure 4.  Quotient velocity plot for mixed type inhibition. The lines were drawn in accordance with Equation (6). The following values of parameters were used: K_m = 1, K_i = 2, and K’_i = 4. The substrate concentration is indicated by each line.

Table 1 summarizes values of the intersection points and slopes of the four types of inhibition.

Table 1.  Values of intersection points and slopes of quotient velocity plots.

Inhibition type	Intersection of lines at two or more values of [S]	Slope
Competitive (Km ≠ K’m)	–Ki at abscissa	Km/[S]·1/Ki
Noncompetitive (Km = K’m, Ki = K’i)	(–Ki, −1) third quadrant	(Km/[S] + 1)/Ki
Uncompetitive (Ki = ∞, K’m = 0)	Parallel	1/K’i
Mixed type (Km ≠ K’m, Ki ≠ K’i)	(–K’i, –Ki/K’i) third quadrant	(Km/[S]·1/Ki + 1/K’i)

Discussion

The first step when analyzing enzyme kinetics is determination of the K_m and V values. The purpose of the analysis of enzyme inhibition is determination of the inhibition type and inhibition constants, which has been achieved using several graphical methods^[1,3–7]. The Dixon plot^[1] is the most widely used method, but cannot distinguish unambiguously between competitive and mixed type inhibitors^[2]. Thus, kinetic analysis of enzyme inhibition has been carried out by concomitant use of the Dixon plot and an improved method presented by Cornish-Bowden^[3].

The “quotient velocity plot” presented in this article can be applied to all types of inhibition. We can determine the inhibition type using inhibition curves at two or more values of substrate concentration. The intersection of this plot varies depending on the inhibition type: straight lines converging on the abscissa at –K_i show competitive inhibition, and parallel straight lines with a slope of 1/K_i give uncompetitive inhibition. On the other hand, quotient velocity plots of noncompetitive inhibition and mixed inhibition give straight lines intersecting in the third quadrant, but one can distinguish between the two types of inhibition. The intersection of the plots in mixed inhibition gives [I] = –K_i and (V – v)/v = –K_i/K’_i. However, the intersection in noncompetitive inhibition occurs at a point where [I] = –K_i and (V – v)/v = –1 because K_i = K’_i in this type of inhibition. A graphical method of this type was described by Hunter and Downs^[8] more than half a century ago, but their method was not particularly convenient as it involved extrapolation of a curve. Thereafter, the combination plot, a new version of the Hunter and Downs method, was presented for analysis of each type of inhibition^[9]. Cortés et al.^[10] further provided a comparison of inhibition plots, in particular Dixon plots and the Cornish-Bowden method, although their study was primarily concerned with relationships between inhibition constants and the concentrations for half-inhibition often used in pharmacology. A similar type of the present quotient velocity plot was also proposed as an analysis method for substrate-inhibited microbial growth^[11]. However, application of the method to other enzyme inhibition was not examined.

The present plot serves as a useful graphical method for determining inhibition types and inhibition parameters, although it requires V values for calculation. This plot can contribute to analysis of the inhibition mechanism in enzyme research and drug action in medicinal chemistry. However, recent studies show that a variety of enzymes do not obey Michaelis–Menten kinetics, and non-Michaelian enzymes cannot be analyzed by linear transformation methods. Various linearization methods including the present plot, Dixon plot, and Cornish-Bowden plot should be used only for initial orientation regarding the action of a substrate/inhibitor on Michaelis–Menten type enzymes. Nonlinear analysis with computer simulation methods will be necessary for detailed kinetic studies.

Declaration of interest: The authors report no conflicts of interest.