Development of a Livestock Odor Dispersion Model: Part I. Model Theory and Development

ABSTRACT

A livestock odor dispersion model (LODM) was developed to predict mean odor concentration, odor frequency, instantaneous odor concentration, and peak odor concentration from livestock operations. This model is based on the Gaussian fluctuating plume model and has the ability to consider the instantaneous concentration fluctuations and the differences between odor and traditional air pollutants. It can predict odor frequency from the routine hourly meteorological data input and deal with different types of sources and multiple sources. Also, the relationship between odor intensity and odor concentration was incorporated into the model.

IMPLICATION

The LODM is a model developed especially for odor from livestock buildings and manure storage. It has the ability to consider short time odor fluctuations, which is important from research and management perspectives. The weighted odor-exceeding half-width method used in LODM to predict odor frequency is an improvement over past studies. The model can accept routine hourly meteorological input and deal with different and multiple sources. It can also consider the relationship between odor concentrations and intensity. These characteristics of LODM make it especially relevant for odor research and application.

INTRODUCTION

Researchers have used industrial air dispersion models to predict livestock odors downwind of livestock operations since the 1980s. The main drawback of these industrial air dispersion models is that most of them can only calculate long time average concentration. However, a series of short exposures to detectable odors can cause nuisances and generate community complaints although the hourly averaged concentrations remain at very low or undetectable levels (<1 odor unit [OU]/m³). This drawback can be overcome by a fluctuating plume model proposed by Gifford1 because of its ability to account for short averaging time fluctuations.

Little research has been carried out to adapt and evaluate fluctuating plume models to predict odor dispersion. Hogström2 first proposed a fluctuating plume model to predict odor frequency that was based on the principles published by Gifford.1 The comparisons between predicted and observed odor frequencies indicated that it is possible to make a realistic prediction of odor frequencies near a point source. Bree and Harssema3 modified Hogström's model and evaluated it with a field measurement around a point source, a building source, and an area source. They concluded that the modified model was superior to Gaussian models for estimating odor exposures based on hourly averages. Mussio et al.4 developed a fluctuating plume dispersion model to predict the odor-impact frequencies in the communities surrounding elevated point sources. Their model provided good simulation of total frequencies of occurrence when the odor occurrence was frequent.

The above studies have shown that the fluctuating plume model, even without considering in-plume fluctuations, could be an effective tool for the prediction of odor dispersion at short distances downwind from the odor sources. Within that short range, the meandering of the plume has a greater effect on odor concentration fluctuations than the in-plume fluctuations.3 Therefore, it will not result in large errors when used to predict odor frequency without considering in-plume fluctuations. Moreover, the near-source distances correspond to the most relevant zone for livestock odors because such odors typically do not travel far distances, in contrast to industrial air contaminants. Hence, the fluctuating plume model that could provide better estimations of odor frequency compared with normally used Gaussian plume models needs to be seriously considered as a tool to predict odor dispersion from livestock operations. A livestock odor dispersion model (LODM) has been developed based on the fluctuating plume model to consider the short time odor fluctuations and to predict the odor dispersion (odor concentration and odor frequency) from livestock operations.

MODEL THEORY

Gaussian Fluctuating Plume Model

The traditional Gaussian plume dispersion model assumes that the average (hourly) concentration of a contaminant downwind of a source and perpendicular to the mean wind direction is normally distributed and centered along the wind direction from that source (Figure 1a).4 However, a short averaging time plume has the appearance of a fluctuating plume in which the plume meanders in the lateral and vertical directions because of the spatial distribution of large eddies in the flow (Figure 1b). The center of the instantaneous (short averaging time) plume fluctuates around the axis of the steady or long-term average plume in an irregular manner.5 The fluctuating plume model has thus been proposed to account for the presence of the instantaneous plumes.

Figure 1. (a) Aerial view of Gaussian plume model, (b) aerial view of fluctuating plume model, and (c) standard deviations of crosswind distances in the fluctuating plume model. Adapted with permission from Mussio et al.4 Copyright 2001 Elsevier, Atmospheric Environment.

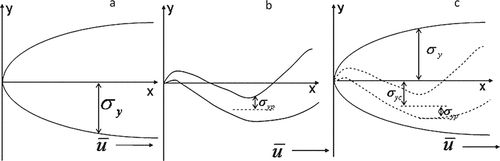
The basic theory of the fluctuating plume model is that the total dispersion can be separated into two components: one that represents the relative dispersion within the instantaneous plume and the other that accounts for the variance of the centroid of the fluctuating plume (Figure 1c).5 The variation due to the fluctuations of local axis and the dispersion within the instantaneous plume are related to the dispersion of the long-term average plume (σ²), which can be mathematically expressed as (eqs 1a and 1b)1

(1a)

(1b)

Mean Odor Concentrations

The mean odor concentrations or hourly averaged odor concentrations are calculated by the basic Gaussian plume model. It can be expressed as (eq 2)5

(2)

where Q is the source emission rate (g/sec); C is the down-wind concentration at the receptor location (x,y,z) (g/m³); U is the average horizontal wind speed (m/sec); h _e is the effective emission height (m); and σ_y and σ_z are the dispersion parameters, or standard deviations (transversal and vertical), of the plume dimension (m), which are functions of the downwind distance x and atmospheric stability.

Instantaneous Odor Concentrations

Gifford1 argued that it is reasonable to assume that the concentration distribution within the instantaneous plume is also Gaussian. Considering the reflection of a ground level, the instantaneous or short averaging time odor concentration C in a receptor (x, y, z) downwind from an elevated point source can be calculated by the following equation from the fluctuating plume model (eq 3):

(3)

where Q is the source odor emission rate (odor units [OU]/sec), ū is the hourly average wind speed at the effective stack height (m/sec); σ_yp and σ_zp are the horizontal and vertical standard deviations of relative dispersion within the instantaneous plume (m), respectively; and y _i is the crosswind distance from the center of the fluctuating plume to the receptors (m), which can be calculated from y – y _c. y _c and h _i are the locations of the center of the instantaneous plume (m). They are also assumed to have a normal probability density function with the standard deviations of σ_yc and σ_zc, shown as (eqs 4 and 5)5

(4)

(5)

Odor Frequency

From eq 3, the instantaneous odor concentrations can be calculated given random generated values of y _c and h _i on the basis of their respective standard deviations and the locations of receptors. Then the frequency of a certain odor level during a 1-hr period can be derived from the calculated subhour concentrations. In the fluctuating plume model developed by Mussio et al.,4 200 random values were generated during a 1-hr period to calculate the frequency. Results showed that this method was effective at estimating the odor frequency. However, this frequency is based on random values, which increases its uncertainty. Hogström2 brought up the concept of weighted odorous half-width to account for the vertical meandering of the plume and used an empirical formula to calculate the ground-level odor frequency. This concept was also used by Bree and Harssema.3 In their model, the ground-level odor frequency was produced by considering the plume horizontal meandering. The method proposed in this study follows that of Bree and Harssema,3 but it has been improved to account for more specified attributes of livestock odor dispersion. It can estimate the odor frequency for any odor level at any height of receptors (not only ground level) from any type of individual and multiple emission sources. The model developed in this study is specifically adapted to livestock odor emitted from animal building and manure storage facilities.

Equation 3 can be solved for y _i, which describes the local instantaneous half-width of the area at a level z that the odor is exceeding a certain level under a given set of meteorological conditions, a specific odor emission rate, and a local instantaneous height h _i. The result of that calculation is named the “odor-exceeding half-width.” This concept is adapted and improved from the odorous half-width, which was proposed by Hogström2 to indicate the local, instantaneous odorous area at the ground level. As shown in Figure 2a, the local plume centroid has an ever-changing height (h _i), and the odor-exceeding half-width is y _i. When the plume ascends or descends to some distance, the odor-exceeding half-width reaches zero, as shown in Figure 2b. With the aid of eq 3, the maximum height (h _max) and minimum height (h _min) can be determined with y _i = 0.

Figure 2. Schematic diagrams of cross sections of the odor-exceeding part of the instantaneous plume at different heights (h _i) and the associated instantaneous odor-exceeding half-width (y _i): (a) 0 < hi < hmax; (b) hi = hmax; (c) hi = 0. Adapted with permission from Bree and Harssema3 Copyright 1987, Kluwer.

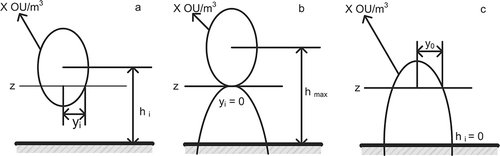
Taking into account the effect of the ground surface, the instantaneous height of a plume cannot fall below ground level, then a value of y ₀ is obtained for h _i = 0, as shown in Figure 2c. Now, the value of y _i is calculated for N equally spaced values (Δh) of h _i between h _i = 0 and h _i = h _max. In LODM, N is set to 100. Then the weighted odor-exceeding half-width can be determined as the sum of the product of each y _i value and its probability (eq 6),

(6)

where P _i can be defined as the portion of time that the local plume height h _i is confined to a given interval, . With the aid of the probability distribution of the value of h _i, which is given by the normal distribution defined by the hourly averaged vertical position of the plume center line (the effective stack height, h _e) and the value of σ_zc, P _i is determined by the following expression (eq 7):

(7)

P ₀ has the expression of (eq 8)

(8)

P _i and P ₀ can be shown as the shadow area beneath the normal distribution of the value of h (Figure 3a).

Figure 3. Schematic diagrams of the portion of time for (a) the different odor-exceeding widths and (b) the odor frequency.

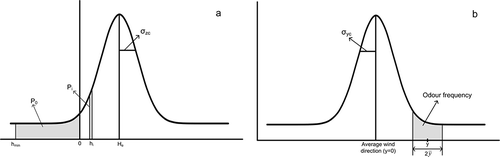
In the fluctuating plume model, the crosswind horizontal position of the local instantaneous plume centroid meanders around the averaged horizontal position (hourly mean wind direction) of the steady plume axis. At an arbitrary location R(x,y,z), the odor frequency is the portion of time during which the horizontal position of the local instantaneous plume centroid is located in the range to . With the aid of the normal distribution of the value of the horizontal position of the local plume, the odor frequency is shown as the shadow area in Figure 3b, and it is calculated by the following expression (eq 9):

(9)

Peak Odor Concentration

From eq 3, the maximum odor concentration occurs when y _i = 0 and h _i = 0 or z. It means that at a receptor, the maximum odor concentration occurs when the fluctuating plume center line is horizontally at the location of the receptor and vertically at ground level or at the receptor height. Hence, the maximum odor concentration takes the form of

(10)

or

(11)

The peak odor concentration is the maximum value of C _max values calculated from eqs 10 and 11.

Therefore, the peak-to-mean ratio that has a great relevance in the area of livestock odor can be easily determined. This ratio depends on the short time dispersion coefficients, hourly dispersion coefficients, and location of the receptor. For the ground-level receptors, without considering the restriction effect of mixing layer, the peak-to-mean ratios can be described as

(12)

Arya5 referred to the ratio of the maximum center line concentrations in fluctuating and steady plumes as the ratio of peak to average concentration, which takes the same form as eq 12.

Stack-Tip Downwash and Plume Rise

If odor is emitted from an elevated point source, the stack-tip downwash and plume rise will be calculated. The calculations follow the procedures described in the Industrial Source Complex model,6 which used the Briggs model to estimate the plume rise.

Dispersion Coefficients

Hogström2 developed a series of general formulas to carry out the calculation of 1-hr (mean) (σ_y andσ_z) and short time (σ_yp and σ_zp) dispersion parameters from experiments conducted in Sweden for elevated point continuous release. At the same time, a method was proposed for ground-level release. The Hogström2 dispersion coefficients depend on the distance and the stability condition. It must be noted that the stability used in the calculations is different from the Pasquill–Gifford stability. The Hogström2 stability parameter is defined as (eq 13)

(13)

in which ∂θ/∂z is the vertical gradient of potential temperature at the level of the plume center (K/m) and u _f is the wind speed at the top of the friction layer (m/sec). Both parameters cannot be obtained directly from routinely observed meteorological data. Therefore, the profiles of the vertical gradient of temperature and wind speed need to be characterized so that the Hogström2 stability parameter can be achieved. In LODM, the Monin–Obukhov similarity theory was used to estimate the vertical profile of wind speed and vertical gradient of potential temperature.7

MODEL DEVELOPMENT

Model Development Procedures

The fundamental steps in developing the LODM to calculate instantaneous odor concentration, peak odor concentration, and odor frequency of a certain level odor are as follows:

1.	Input source data, meteorological data, and receptor locations;
2.	Derive parameters involving friction velocity, latent heat flux, and Monin–Obukhov length for the planetary boundary layer (PBL);
3.	Calculate wind speed profile, vertical gradient of potential temperature, and the Hogström stability parameter;
4.	Calculate stack-tip downwash and plume rise for a point source;
5.	Calculate long-term plume dispersion coefficients; and
6.	Calculate short time plume dispersion coefficients.

To calculate instantaneous odor concentration, the model generates random values for location of the instantaneous plume center line and then calculates the instantaneous odor concentrations by assuming Gaussian distribution of odorous pollutants within the fluctuating plumes.

Peak concentration is calculated by setting fluctuating the plume center line at ground level or receptor height and the horizontal distance to a receptor to be zero. The odor frequency is calculated by the method of the weighted odor-exceeding half-width (eq 9).

Adapting the Model for Livestock Odor Dispersion

The fluctuating plume model proposed above to estimate odor concentration and odor frequency is adapted for the modeling of livestock odor dispersion by taking into account the different characteristics of various livestock odor sources and the persistence of different types of livestock odors.

Odor Emission from an Elevated Stack

If the odor is emitted from an elevated stack, the source can be treated as a point source with a physical stack height. The plume rise will be calculated with the Briggs plume rise formula.

Odor Emission from an Animal Building

Odor emission from an animal building comes from the exhaust air outlets, which are the openings on the walls and roofs of the building and the wall- or ceiling-mounted fans. There are often several vertical or horizontal openings or fans for one building. Because of the complicated and variable pattern of the openings and fans and the effect of the building, it is reasonable to consider the building source as a whole volume source.

A virtual point source algorithm is used to model the odor released from volume sources. An imaginary or virtual point source is located at a certain distance upwind of the volume source (called the virtual distance) to account for the initial size of the volume source plume. Therefore, the equations used for a point source are also applied to calculate odor concentrations and odor frequencies produced by volume source emissions.

The initial lateral (σ_y0) and vertical (σ_z0) dimensions should be assigned. Normally, it can be determined from the building dimension (eqs 14a and 14b).

(14a)

(14b)

in which W is the width of the building measured along a direction perpendicular to that of the wind (m) and H is the height of the building (m).

The virtual lateral (x _y) and vertical distance (x _z) can then be calculated with the aid of the initial dimensions and the formulas of the dispersion coefficients' calculation. The concentrations or frequency in a downwind distance can be calculated by the same equations as used for a point source, with the modification of (eqs 15a and 15b)

(15a)

(15b)

Odor Emission from Manure Storage

A manure storage facility can be treated as an area source that can be reduced to a volume source having a given width (W) and for which H = 0.

Multiple Sources

The odors emitted from livestock operations often come from multiple sources, and, as a result, they may have different persistences, which means that after the same dilution, the odor strengths are different. Then their combined impacts on receptors are very difficult to be evaluated. A simple and coarse method is used by the LODM to account for multiple sources when dealing with odor concentrations. However, this method should be improved through further research on the combination of the impacts of odors having different persistences. Consider two odor sources (source 1 and source 2) having emission rates of Q1 and Q2, respectively, and having a combined odor impact on a receptor. Under certain meteorological conditions, the concentrations of odor from these two sources are X1 and X2, respectively. If both odors have the same persistences, then the odor concentration at the receptor will correspond to X1 + X2. The contributions from these two sources can then be converted into one from only one source (e.g., source 1) by combining an emission rate, Q, into this source (source 1) that has the same impact as the other (source 2), in which (eq 16)

(16)

However, this method is not applicable when calculating odor frequency from multiple sources. Another simple and effective method is proposed to estimate the odor frequency from multiple sources. If there are two sources that contribute to a receptor, the odor frequencies from each source that exceeds a certain level (c ₀) are p(c ₁ ≥ c ₀) and p(c ₂ ≥ c ₀) respectively. Then the total odor frequency from these two sources can be expressed as (eq 17):

(17)

The detailed derivation of this equation can be found in the Appendix. If there are more than two sources, the following procedure can be taken to estimate the overall frequency. First, the odor frequency from any two sources is calculated using the method above, and then this calculated odor frequency is assumed to be the result from one source and is combined with the odor frequency from the third source to get the odor frequency from these three sources. This procedure can be extended to any given number of individual sources to estimate the overall odor frequency from multiple sources (n > 2).

Persistence of Different Odors

An important difference between odor and traditional air contaminants is that various odors have different persistences. This means that the intensity of various odors that have the same initial intensity can be different at the same dilution levels. Therefore, the persistence of odors is an issue that needs to be resolved when conducting odor dispersion modeling. Furthermore, the field measurement of an odor plume is always recorded in intensity, whereas the model predicts odor concentrations or odor frequencies of certain odor concentrations.

Therefore, it is necessary to include the relationships between odor concentration and intensity into the model to consider the difference between odor and gas and to evaluate the model-predicted concentration or frequency. Many existing relationships obtained from previous studies are provided in the model. Users can select one of the relationships or parameterize other specific relationships to do the conversion between odor intensity and concentration. However, one should be cautious when using laboratory-derived relationships for conversion of field intensity into odor concentration, as pointed out in the study of Zhang et al.,8 which showed that field-measured odor intensity does not correlate well with odor concentrations measured with olfactometers in the laboratory. It would be better to obtain such a relationship from field odor concentration data collected using field odor measurement methods (i.e., scentometer method) and field-measured intensity data.

CONCLUSIONS

The LODM is a specifically designed model for livestock odor. It was developed based on a Gaussian fluctuating plume model; therefore, it has the capability to predict instantaneous odor concentration, peak odor concentration, and odor frequency. In the model, odor frequency is calculated by a weighted odor-exceeding half-width method. This method is an improvement of the weighted odorous half-width method used by de Bree and Harssema3 and it has an advantage over that used by Mussio et al.,4 who calculated the odor frequency from instantaneous odor concentrations. Also, a simple and effective method is created to calculate odor frequency of multiple sources from the odor frequency of an individual source. When adapting a Gaussian plume model for livestock odor sources, a virtual point source method is used to deal with area and volume sources. The relationships between odor intensity and odor concentration are also included in the model to account for the difference between odor and traditional air pollutants. The model evaluation and validation with field odor plume measurements will be presented in the second part of this research.9

ACKNOWLEDGMENTS

This study was financially supported by the Natural Sciences and Engineering Research Council of Canada and the University of Saskatchewan.

APPENDIX

The odor frequency calculated by the weighted odor-exceeding half-width method takes the form of (eq 18)

(18)

in which is the function of the certain level of odor concentration.

If there are two sources that contribute to a receptor, the odor frequency from each source that exceeds a certain level (c ₀) can be expressed as (eqs 19a and 19b)

(19a)

(19b)

in which f(y) and g(y) refer to the general form of , which are the functions of cross-wind distance y; a(c ₀) and m(c ₀) are the general forms of , which are the functions of certain level odor c ₀; and b(c ₀) and n(c ₀) are the general forms of , which are also the functions of c ₀.

To calculate the odor frequency of multiple sources, which is p(c ₁ + c ₂ ≥ c ₀), the range of 0 to c ₀ is separated into N equal pieces, in which each piece has a value of Δc. If the odor concentration from one source is equal or greater than c _0, then the total odor concentration from two sources will be equal or greater than c ₀ regardless of the odor concentration from the second source. Under this circumstance, the total odor frequency will be p(c ₁ ≥ c ₀)·p(c ₂ ≥ c ₀) or p(c ₁ ≥ c ₀). If the odor concentration from one source is within the range from (c ₀ -Δc) to c ₀, the total odor concentration will be equal to or greater than c ₀ only if the odor concentration from the second source is equal to or greater than Δc. Therefore, the total odor frequency will be p(c ₀ ≥ c ₁ ≥ (c ₀ -Δc))·p(c ₂ ≥ Δc). By the same token, the total odor frequency can be obtained as (eq 20)

(20)

Substituting p(c) from eq 18 into eqs 19, the total odor frequency can be expressed as

(21)

After some algebraic transformations, it becomes (eq 22)

(22)

Yu,Guo,and Laguё

It can be integrated as

(23)

Equation 23 is the general form of calculating the odor frequency from two sources.

To simplify the calculation, especially for more than two sources, Δc = c ₀ is assumed to get (eq 24)

(24)