An Analysis of Extinction Coefficients of Particles and Water Moisture in the Stack after Flue Gas Desulfurization at a Coal-Fired Power Plant

ABSTRACT

Two important factors that affect in-stack opacity—light extinction by emitted particles and that by water moisture after a flue gas desulfurization (FGD) unit—are investigated. The mass light extinction coefficients for particles and water moisture, k _p and k _w, respectively, were determined using the Lambert-Beer law of opacity with a nonlinear least-squares regression method. The estimated k _p and k _w values vary from 0.199 to 0.316 m²/g and 0.000345 to 0.000426 m²/g, respectively, and the overall mean estimated values are 0.229 and 0.000397 m²/g, respectively. Although k _w is 3 orders of magnitude smaller than k _p, experimental results show that the effect on light extinction by water moisture was comparable to that by particles because of the existence of a considerable mass of water moisture after a FGD unit. The mass light extinction coefficient was also estimated using Mie theory with measured particle size distributions and a complex refractive index of 1.5-ni for fly ash particles. The k _p obtained using Mie theory ranges from 0.282 to 0.286 m²/g and is slightly greater than the averaged estimated k _p of 0.229 m²/g from measured opacity. The discrepancy may be partly due to a difference in the microstructure of the fly ash from the assumption of solid spheres because the fly ash may have been formed as spheres attached with smaller particles or as hollow spheres that contained solid spheres. Previously reported values of measured k _p obtained without considering the effects of water moisture are greater than that obtained in this study, which is reasonable because it reflects the effect of extinction by water moisture in the flue gas. Additionally, the moisture absorbed by particulate matter, corresponding to the effect of water moisture on the particulates, was clarified and found to be negligible.

IMPLICATIONS

In-stack opacity is used as a surrogate for particle concentration and can be measured using light transmission meters as part of a continuous emission monitoring system. Because emission standards have become increasingly strict, FGD with wet scrubbing is generally used for coal-fired power plants. However, after a FGD unit with wet scrubbing is set up, the concentration of water moisture increases, affecting the measured opacity. This study evaluates the contributions of particles and water moisture to opacity. The results should provide useful information and can be utilized for modifying measurements for monitoring particulate emissions using opacity.

INTRODUCTION

Opacity is defined as the percentage of transmitted light that is obscured as it passes through a medium. The obscuration is caused by extinction, which consists of absorption and scattering by constituents in the medium.1,2 In a coal-fired power plant, in-stack opacity is generally measured in situ using light transmission meters as part of a continuous emission monitoring system (CEMS). Opacity is a function of particulate concentrations and many other independent optical and physical variables, such as particle size distribution, particle density, refractive index of particles, and nitrogen dioxide and sulfuric acid concentration in the exhaust gas, as examined in previous studies. The extinction of a constituent is usually expressed in terms of mass extinction coefficient (k),3,4 the extinction coefficient (k multiplied by concentration), or the ratio of specific particulate volume to mass extinction coefficient (K).5–9 The Lambert-Beer law states that opacity due to constituents that contribute to the decay of intensity in a collimated beam with an optical path length (L) can be expressed as³

(1)

where W is the mass concentration, k is the mass extinction coefficient (m²/g), K is the ratio of the volume of a specific particulate to the mass extinction coefficient (cm³/m²), ρ is the density of the substance, and subscript i denotes the contribution of species i. k and K are dependent on the composition, size distribution, relative refractive index, and the beam wavelength. The Lambert-Beer equation applies at conditions in which multiple scattering is negligible.

For experiments on a Kraft mill recovery furnace, Bosch5 and Larssen et al.6 utilized a bolometer and a smoke meter, respectively, to compare the theoretical and measured opacities due to particles. The calculated K values for 18 tests were in the range of 0.80–1.20 cm³/m²; the variation was due to variations in the size distribution parameters. Thielke and Pilat7 conducted simultaneous measurements of the in-stack opacity, particle mass concentration, and particle size distribution of a hogged-fuel boiler, a Kraft recovery furnace, and a pulverized coal-fired boiler to assess the validity of the particle mass concentration-opacity relationship. The results of their study indicate the importance of using the actual particle size distribution (particle diameter range of 0.2–10 μm) for predicting the relationship between transmittance and mass concentration. Ensor and Pilat8 studied the effects of particle size on opacity using the Lambert-Beer law to determine the parameter K at a coal-fired power plant. Their results showed that K is primarily a function of particle size for particles with radii greater than approximately 0.5 μm and is primarily a function of the refractive index for smaller particles. They also studied the effect of particle size distribution on light transmittance measurements.9 The ratio of the expected extinction coefficient to the theoretical extinction coefficient was reported to be a function of the log-normal size distribution parameters (geometric mass mean radius and geometric standard deviation) for various detector acceptance angles. Cowen et al.10 measured the fly ash light absorption for coal-fired boilers with the integrating plate method. They analyzed the absorption of fly ash samples from four types of coal-fired power plants with various unit ratings and studied the theoretical modeling of smoke plume opacity. By the integrating plate method, which is defined as comparing the light absorption through a clean blank filter to one with a single layer of aerosol, only absorption is measured and the scattering effect is diminished. Steig and Pilat11 performed simultaneous measurements of in-stack light transmittance, particle mass concentration, and particle size distribution at a pulverized coal-fired boiler. The measured values of K, which ranged from 0.68 to 0.90 cm³/m², were consistently lower than the theoretically calculated values because of an assumed particle density of 1 g/cm³. Conner and Knapp12 evaluated the particle concentration and light attenuation for coal-fired power plants with electrostatic precipitators (ESPs); the value of K varied from 0.11 to 7.50 cm³/m². Pilat and Ensor13 measured and calculated the light extinction versus aerosol mass concentration relationship for atmospheric and source emission aerosols. The measured values of K ranged from 0.26 to 0.49 cm³/m² and from 0.06 to 0.78 cm³/m² for atmospheric aerosol and individual source emission, respectively. In addition to the effects due to particles, the emissions of sulfur trioxide (SO₃) were a key component of opacity and acid deposition and need to be low enough to not cause opacity violations and acid deposition.14 The emission of SO₃ depended on the sulfur content in coal, combustion conditions, flue gas characteristics, and air pollution devices. Pilat and Wilder15 calculated the effect of the initial water and sulfuric acid (H₂SO₄) concentrations and final gas temperature on the opacity after cooling from an original stack gas temperature at 300 °C and found significant effects for initial H₂SO₄ concentrations greater than 5 parts per million (ppm). They further evaluated the effects of particle size and found that H₂SO₄ condensation should have minimal effects on particles greater than 1 μm.16 Lou et al.17 established an empirical equation similar to Beer's law that was used to predict the plume opacity in terms of the stack diameter and concentrations of particles and total water-soluble sulfates. Meng et al.18 presented a computer simulation model that calculates the opacity due to primary particles emitted from the stack and secondary particles that form (such as SO₃ hydrolyzes to H₂SO₄, hydrochloric acid [HCl], and ammonia [NH₃]) in the atmosphere after the release of condensable gases from the stack. Lindau³ measured the effect of nitrogen dioxide (NO₂) on the flue gas opacity and demonstrated that for a coal-fired boiler with a NO₂ concentration of approximately 10–50 ppm, the effect is approximately 2–10%. Wieprecht et al.19 concluded that the water droplets within the flue gas after a flue gas desulfurization (FGD) unit were mainly formed via condensation onto fly ash particles. Although mist eliminators for coarse and fine droplets are highly efficient in FGD, some water moisture still remains.

The above literature illustrates that in-stack opacity is strongly correlated with various factors such as particle mass concentration, particle size distribution, and particle density as well as the H₂SO₄ and NO₂ concentrations. The concentration of water moisture increases after a FGD unit with wet scrubbing is installed, but the effect of water moisture on opacity has not been fully evaluated. In the study presented here, experiments were conducted at a full-scale coal-fired power plant to analyze the effects of particles and water moisture on opacity. The parameters K _p and K _w (subscripts p and w denote particles and water moisture, respectively) and the mass extinction coefficients k _p and k _w for emitted particles and water moisture, respectively, in the flue gas that leaves a FGD unit were determined. The parameters of K _p and K _w were determined using nonlinear least-squares regression and Newton's method with the Lambert-Beer equation. To clarify the effect of water on the characteristics of particulates, which subsequently affect the extinction coefficient of particles, particle hygroscopicity was also examined.

It was found that fly ash consists of a mixture of particles with different chemical compositions and thus different optical properties.20 Most fly ash particles are spherical and glassy because of the rapid cooling of the molten droplets formed during combustion. And most particles are observed to be highly transparent at visible wavelength, whereas a small fraction (generally un-burned carbon or iron oxides) are observed to be entirely opaque. Boothroyd et al.21 measured the light-scattering phase functions and asymmetry factors for a sample of fly ash and compared them with Mie theory predictions. The results imply that fly ash could be treated as spherical particles under furnace conditions at which they were well dispersed. The complex refractive index (or optical constants) may be used together with Lorenz-Mie theory to predict the absorption, extinction, and scattering properties of particles under assumption of an equivalent sphere model and vice versa. In addition to the empirical results, this study also estimated the parameters K _p and k _p on the basis of the Mie theory using the computational BHMIE program22,23 and existing data of complex refractive index for fly ashes under a spherical particle approximation. The estimations were compared with the experimental results of the study presented here.

EXPERIMENTS

Basic Information of the Power Plant and In-Stack Instruments

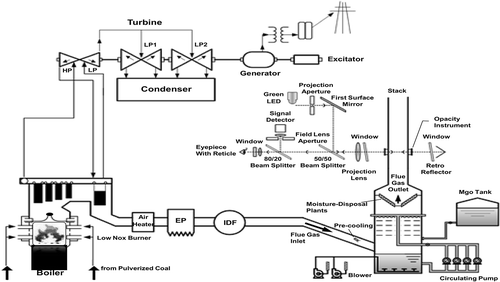
In the study presented here, experiments were conducted in a commercialized coal-fired power plant with a FGD unit with a wet scrubber, as shown in Figure 1. The plant comprises a coal-fired boiler, steam turbines, and a 14.3-MW generator. The FGD unit is downstream of an induced-draft fan (IDF), and an ESP is upstream of the IDF. Exhaust gas enters the FGD unit and is scavenged by precooling and circulating water and further passes through de-misters to the opacity measurement instrument. Table 1 lists basic information about the test stack at the power plant. The sampling sites were located in the vertical stack 50 m above the ground. The optical cross-stack transmissometer monitor was located 1.2 m below the sampling ports.

Figure 1. Schematic diagram of the coal-fired power plant used in experiments.

Table 1. Basic information on the power plant

Parameter	Basic Information
Analysis of coal
Coal type	Subbituminous
Total moisture (as received)	8.89%
Inherent moisture (air-dried basis)	2.01%
Sulfur content (air-dried basis)	0.88%
Volatile matter (air-dried basis)	31.3%
Ash (air-dried basis)	15.2%
Heating value (air-dried basis)	1570 kJ/kg
Boiler conditions
Boiler type	Four radiative burner units
Coal flow	∼1.45–1.72 kg/sec
Main steam pressure	∼119–120 kg/cm^2
Main steam flow	∼11.8–13.4 kg/sec
Air pollution control equipment	Low-NOx burner (LNB)
	ESP
	FGD
Stack parameters
Stack height	70 m
Stack diameter	2.4 m

Experimental Method and Procedure

To evaluate the effects of various constituents on in-stack opacity, particle mass concentration; water moisture concentration; gaseous oxides of sulfur (SO_x), nitrogen (NO_x), and oxygen (O₂) concentrations; flow rate; flue gas temperature; the circulating water pH of FGD; H₂SO₄; and opacity were measured simultaneously for each run. The factors were varied by changing ESP currents, the FGD unit operating conditions, and boiler loads, respectively. The ESP currents were regulated to produce various particle concentrations, the precooling and circulating water in the FGD unit were adjusted to produce various mass concentrations of water moisture in the flue gas, and the boiler loads were adjusted by changing the input rate of the coal feeder. When the effect of a load was to be analyzed, the other two loads were set to a relatively steady state to systematically and quantitatively examine its effect on opacity. Note that the operation conditions were limited to those that could not exceed the Republic of China Environment Protection Administration (ROC EPA) emission standards. The in-stack opacity, water moisture, and particle mass concentration were measured simultaneously under various conditions of the boiler load, FGD, and ESP to evaluate their effects on K _p and K _w.

The in-stack instruments include an opacity meter, a CEMS, a thermometer, a flow rate meter, and a pH meter. Opacity was measured by an optical transmissometer using a green light-emitting diode with a wavelength of 550 nm. The readings of opacity were recorded every 6 sec. The value of opacity presented in the following is the average of readings at three 6-min intervals. The CEMS is a lineup of analyzers for the measurement of NO_x, SO_x, and O₂ stack gases emitted from the boilers of a thermo-electric coal-fired power plant. The units are capable of the simultaneous and continuous measurement of various components. The temperature of the flue gas was monitored every minute by a resistance thermometer (RTD, type Pt 100 Ω). The flow rate of the flue gas was monitored every minute by a supersonic flow rate meter.

Flue-Gas Sampling Methods and Analyses

The flue gas was sampled to obtain the mass concentration of particles W _p (mg/Nm³), the mass concentration of water moisture W _w (g/Nm³), and the particle size distribution. In addition to the above factors, particle density, particle chemical compositions, and particle shape were also measured. The isokinetic sampling of the ROC EPA Method 1, a modified method of the U.S. Environmental Protection Agency Method 5 with fiberglass thimbles replacing the fiberglass filter, was used to measure the particle mass concentration. The mass concentration of particles was determined by gravimetric analysis of the samples. The water moisture in the stack flue gas was absorbed by calcium chloride (CaCl₂) pellets, and the water mass concentration was determined by gravimetric analysis. Sampling of the particles by filter method continued for 30 min, and the total sampled flue-gas volume exceeded 500 L. Sampling of the water content took 10 min, and the total sampled flue-gas flow exceeded 10 L for each sample. The particle size distribution was determined using a cascade impactor with nine impactor stages with cut sizes from 0.1 to 10 μm, associated with the gravimetric analysis of the samples. To measure the concentration of H₂SO₄, a sample was obtained from the stack gas through a heated quartz-lined probe. The concentration of H₂SO₄ was determined using a method similar to that utilized in ref 17, and analysis was conducted on an ion chromatograph. The particle density was analyzed using an ultrapycnometer and by applying Archimedes' principle of fluid displacement and Boyle's law. Particle chemical compositions were analyzed using inductively coupled plasma with atomic emission spectroscopy and by performing standard industrial analyses. The particle shapes were determined using a scanning electron microscope (SEM) from the filter tube. All indicated data are averages of at least three repeated runs and include the standard deviation.

The SO_x concentration of the flue gas was controlled using an aqueous magnesium oxide (MgO) solution. The flue gas had passed through the de-mister with an outlet temperature of nearly 50 °C. In the FGD unit, the efficiency of SO_x removal was up to approximately 99%. The experimental measurements show that when the SO_x concentration increased from 21 to 143 ppm, the concentration of H₂SO₄ increased from 3.1 to 7.7 mg/Nm³ and the in-stack opacity increased from 24.6 to 25.2%. Because the variation in opacity with a considerable change in SO_x concentration was less than 0.6% and all experiments in this study were performed at a SO_x concentration controlled to within approximately 20–36 ppm, the effects of SO_x and H₂SO₄ emissions on opacity were thus negligible.

MATHEMATICAL MODEL

Empirical Opacity Equation

For in-stack plumes, the major constituents usually consist of particulate, water moisture, H₂SO₄ steam, and NO₂. In the study presented here, the SO_x concentration is controlled by using liquid MgO in the FGD unit, as mentioned earlier. The effect of associated SO_x and liquid H₂SO₄ emissions on plume opacity is thus neglected.

An empirical correlation equation similar in form to that of the Lambert-Beer equation is then derived in this study. The derived equation is

(2)

where W _p, W _w, and W _NO2 denote the mass concentrations of particles, water moisture, and NO₂, respectively, and ρ_p, ρ_w, and ρ_NO2 are the densities of particles, water, and NO₂, respectively. The parameters K (cm³/m²) and k (m²/g) are defined as described above for species of particulates, water moisture, and NO₂, respectively.

NO₂ has absorption bands in the visible light region and thus affects opacity.3 Equation 2 thus includes the contributions of light extinction by particulates, water moisture, and NO₂ in the flue gas. Equation 2 reduces to the classical equation for cases of light extinction by particulates only when NO₂ and water moisture are not included. The parameters W _p, W _w, W _NO2, ρ_p, ρ_w, and ρ_NO2in eq 2 can be readily obtained from experimental measurements, whereas values of K _p and K _w (or k _p and k _w) need to be determined. According to Lindau,³ 1/(K _NO2 × ρ_NO2) is the mass extinction coefficient k of NO₂, which was measured to be 3.3 × 10⁻⁴ ppm⁻¹ m⁻¹.

Inversion Methodology for Estimating Parameters K _p and K _w

In the study presented here, the least-squares method is used to simultaneously determine the parameters K _p and K _w with measured opacities under various operation conditions.

In the inversion procedure, the squared error, E, is defined as

(3)

where Op _i,e and Op _i,c denote the measured and estimated opacities, respectively.

(4)

and β = K _p, K _w. The values of K _p and K _w are determined by minimizing E. The partial derivation of E with respect to β is expressed as

(5)

Let

(6)

where X is the sensitivity matrix, and the elements of this matrix are called the “sensitivity coefficients.”24 When ∇E = 0, the minimum value of E exists, and the corresponding set of solutions, is given by

(7)

The Taylor series expansion of at b is

(8)

Substituting eq 8 into eq 7 yields

(9)

Equation 9 is applied for the numerical computation of the inverse estimation of parameters. Newton's iteration method is used with initial guesses of b. After iterating k times, the (k + 1)th iteration is started with new parameters:

(10)

and

(11)

The computation continues until the values of K _p and K _w at two consecutive calculations differ by a specified limit.

Theoretical Calculation of the Particle Parameter K _p

Given the wavelength of incident light, particle size distribution, and the complex refractive index of particles, Mie theory can be applied to estimate the particle light extinction efficiency factor, Q _ext, which is defined as the ratio of the extinction coefficient to the cross-sectional area for spherical particles. Hodkinson25 also reported light extinction by nonspherical particles in random motion to be nearly the same as that for spherical particles much larger and much smaller than the wavelength of incident light. In the study presented here, Q _ext is determined using the BHMIE program under an equivalent spheres model.

The theoretical parameter K _p can then be calculated from Mie theory using

(12)

where f(r) is the normalized particle number density, r is the radius of particles, and Q _ext is the particle light extinction efficiency factor.

Estimation of Moisture Droplet Mean Diameter

Moisture molecules may concentrate at temperature drops; they combine to form water droplets. For a mono-dispersion of spherical moisture droplets, the relationship between the mass extinction coefficient and extinction efficiency factor is expressed as

(13)

where Q _wext is the extinction efficiency factor of a moisture droplet determined by Mie theory and r is the radius of the moisture droplet. N is the number of moisture droplets per unit volume and is given from mass concentration of water moisture as W _w/(4πr ³ρ_w/3). The amount of water moisture present in gas can also be described by the expression of relative humidity (RH).

For water moisture, it scatters and does not absorb the beam at the investigated wavelength, and the index of refraction is approximately 1.33. In the Rayleigh scattering regime, the extinction efficiency factor can be further expressed as

(14)

From eqs 13 and 14, the effective mean diameter (2r) of water moisture droplets can be estimated after the mass extinction coefficient k _w is readily determined.

RESULTS AND DISCUSSION

Summary of Flue Gas and Characteristics of Particles

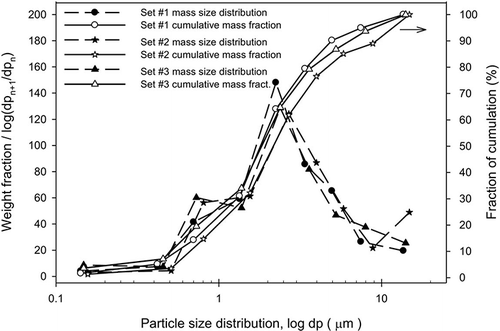
When pulverized coal is burned in a boiler, most of the ash leaves the furnace (as fly ash) with the flue gas. Table 2 shows the composition of flue gas and the constituents of ash under various operation conditions of the boiler load. In this investigation, major components of the fly ash particles included silicon dioxide (SiO₂) (46.9% ± 0.5%) and aluminum oxide (Al₂O₃) (42.7% ± 0.3%); the particles contained approximately 5.8–7.8% unburned carbon by weight. The particle density is 2.66 ± 0.09 g/cm³; this density is assumed to be constant over the range of particle sizes measured and is close to the typical soil density. Figure 2 shows the particle size distributions for particle concentrations of 36.5, 45.6, and 51.5 mg/Nm³, respectively, at various boiler loads. Most of the particles had diameters greater than 0.5 μm, and the mass mean diameter was 4.00 ± 1.03 μm. The SEM micrographs of particles are presented in Figure 3, a and b. The results from the SEM showed that most of the particles less than 5 μm were nearly spherical. Cho et al.26 concluded that fine fly ash particles (<200 mesh) were spherical, whereas the coarse particles (>200 mesh) were mostly irregular and porous, which is consistent with the conclusions of refs 17 and 18 mentioned earlier.

Table 2. Summary of flue gas and particle characteristics

Stack Flue Gas Conditions	Test Data Range
SOx	∼20–36 ppm
NOx	∼150–186 ppm
NO2	∼4.7–5.7 ppm
O2 (at sampling hole of stack)	∼9.3–12.1%
(leaving the G/A heater)	∼3.5–3.8%
Flow rate	∼20.3–23.8Nm^3/sec
Exhaust temperature	48.1∼51.1°C
Water content	∼9.25–12.13%
Particle density	2.66 ± 0.09 g/cm^3
Mass mean diameter	4.00 ± 1.03 μm
Unburned carbon	6.68% ± 1.10%
Ash analysis of oxides
SiO2	46.89% ± 0.53%
Al2O3	42.71% ± 0.26%
Iron(III) oxide (Fe2O3)	3.27% ± 0.34%
Calcium oxide (CaO)	3.33% ± 0.26%
Titanium dioxide (TiO2)	1.59% ± 0.02%
SO3	0.50% ± 0.03%
Potassium oxide (K2O)	0.35% ± 0.00%
Sodium oxide (Na2O)	0.14% ± 0.01%
MgO	0.32% ± 0.03%
Other	0.91% ± 1.23%

Figure 2. Mass and cumulative distributions of emitted particles at various boiler loads.

Figure 3. SEM micrograph of particles collected by filter.

Experimental Data Obtained under Various Operation Conditions

Table 3 presents detailed experimental results for variations of ESPs (Table 3a), FGD (Table 3b), and boiler load (Table 3c) in which the various operation conditions were set by regulating ESP currents, adjusting the precooling and circulating water in the FGD unit, and adjusting the main steam flow rate by changing the feeding rate of coal into the boiler. The baseline condition was set as an ESP current of 200 mA, the FGD unit precooling and circulating water at 0.36 m³/sec, and the main steam flow rate in the boiler at 12.5 kg/sec. From Table 3a, the opacity increased with decreasing ESP current supply. This relationship follows from the fact that increasing the ESP electric current gradually reduced the particle concentration, as revealed by the measured data. From Table 3b, which shows the effects of the operation parameters of the FGD unit, the opacity remained almost constant as the operation of the precooling and circulating water varied because particle mass concentration decreases when water moisture increases and vice versa. From Table 3c, as the coal flow rate increased with the boiler load, the plume opacity increased because the mass concentration of the participating constituents and particularly that of the particles increased.

Table 3a. Data obtained by regulating ESP currents for various particle concentrations

Range	∼100–200 mA (current)
Load	− → +
Particle concentration W p (mg/Nm^3)	110 ± 6	90.8 ± 5.5	79.1 ± 9.0	70.3 ± 8.5	59.2 ± 5.5
Water content W w (g/N m^3)	90.2 ± 0.5	92.8 ± 1.1	91.7 ± 1.0	91.1 ± 0.7	90.0 ± 1.8
NO2 emission (ppm)	5.6 ± 0.1	5.1 ± 0.2	5.4 ± 0.2	5.3 ± 0.3	4.7 ± 0.1
Flue gas temperature (°C)	50.5 ± 0.4	51.1 ± 0.3	50.3 ± 0.6	49.9 ± 0.4	50.9 ± 0.6
Water content X w (%)	11.2 ± 0.1	11.6 ± 0.1	11.4 ± 0.1	11.3 ± 0.1	11.2 ± 0.2
Saturated vapor content X tw (%)	12.7 ± 0.1	13.1 ± 0.3	13.0 ± 0.2	12.3 ± 0.3	13.3 ± 0.2
RH (%)	88.4 ± 0.4	88.1 ± 2.9	88.1 ± 0.5	92.4 ± 2.5	84.3 ± 2.6
Measured opacity (%)	25.7 ± 0.6	24.7 ± 0.4	23.7 ± 0.3	22.7 ± 0.5	20.9 ± 0.6
Theoretical opacity (%)	26.0	24.8	23.7	22.8	21.7
Extinction by particles (%)	40.2	35.1	32.2	29.8	26.7
Extinction by water moisture (%)	56.9	62.1	64.7	66.9	70.2
Extinction by NO2 emission (%)	2.9	2.8	3.1	3.3	3.1

Table 3b. Data obtained by adjusting the FGD unit's precooling and circulating water rate

Range	∼0.27–0.40 m^3/sec (circulating water)
Load	− → +
Particle concentration W p (mg/N m^3)	83.4 ± 8.1	74.2 ± 9.0	70.1 ± 8.9	59.2 ± 5.5	37.8 ± 1.9
Water content W w (g/N m^3)	74.4 ± 1.8	80.3 ± 1.6	81.5 ± 1.7	90.0 ± 1.8	97.5 ± 0.3
NO2 emission (ppm)	4.8 ± 0.1	4.6 ± 0.2	5.3 ± 0.1	4.7 ± 0.1	5.1 ± 0.2
Flue gas temperature (°C)	50.3 ± 0.5	50.1 ± 0.4	49.1 ± 0.5	50.9 ± 0.6	50.4 ± 0.4
Water content X w (%)	9.3 ± 0.2	10.0 ± 0.2	10.2 ± 0.2	11.2 ± 0.2	12.1 ± 0.1
Saturated vapor content X tw (%)	13.4 ± 0.2	12.6 ± 0.4	11.9 ± 0.4	13.3 ± 0.2	13.2 ± 0.5
RH (%)	69.0 ± 2.5	79.6 ± 4.0	85.0 ± 0.7	84.3 ± 2.6	92.3 ± 3.7
Measured opacity (%)	21.5 ± 0.1	21.0 ± 0.4	21.0 ± 0.3	20.9 ± 0.6	21.7 ± 0.7
Theoretical opacity (%)	21.3	21.5	21.4	21.7	21.0
Extinction by particles (%)	38.1	33.8	32.0	26.7	17.7
Extinction by water moisture (%)	58.8	63.2	64.5	70.2	78.9
Extinction by NO2 emission (%)	3.1	3.0	3.5	3.1	3.4

Table 3c. Data obtained by varying the operation condition of the boiler load

Range	∼11.78–13.44 kg/sec (main steam flow)
Load	− → +
Particle concentration W p (mg/Nm^3)	45.5 ± 1.9	59.2 ± 5.5	66.1 ± 1.9	78.7 ± 2.8	96.6 ± 1.7
Water content W w (g/Nm^3)	87.7 ± 0.6	90.0 ± 1.8	94.8 ± 2.6	91.6 ± 1.5	89.6 ± 0.3
NO2 emission (ppm)	5.0 ± 0.4	4.7 ± 0.1	5.0 ± 0.4	5.3 ± 0.2	5.7 ± 0.1
Flue gas temperature (°C)	48.1 ± 0.4	50.9 ± 0.6	49.3 ± 0.2	50.3 ± 0.6	49.3 ± 0.4
Water content X w (%)	10.9 ± 0.1	11.2 ± 0.2	11.8 ± 0.3	11.4 ± 0.2	11.2 ± 0.1
Saturated vapor content X tw (%)	11.1 ± 0.1	13.3 ± 0.2	12.0 ± 0.1	11.9 ± 0.5	11.6 ± 0.2
RH (%)	98.7 ± 1.2	84.3 ± 2.6	98.2 ± 2.6	95.6 ± 4.0	96.1 ± 0.9
Measured opacity (%)	19.8 ± 0.3	20.9 ± 0.6	22.7 ± 0.3	24.6 ± 0.7	25.6 ± 0.3
Theoretical opacity (%)	20.2	21.7	23.0	23.6	24.9
Extinction by particles (%)	22.3	26.7	27.9	32.1	37.2
Extinction by water moisture (%)	74.2	70.2	69.1	64.8	59.7
Extinction by NO2 emission (%)	3.5	3.1	3.0	3.1	3.1

Inversion Estimations of Parameters K _p, K _w, k _p, and k _w

The values of parameters K _p and K _w were determined from the experimental data in Table 3 using the inversion methodology described above. The results show that the values of K _p and K _w were 1.642 and 2520 cm³/m², respectively, corresponding to k _p and k _w values of 0.229 and 0.000397 m²/g, respectively. Although K _p and K _w differ by 3 orders of magnitude, the effect of extinction by water moisture is comparable to that by particles or even greater because of the existence of a considerable mass of water moisture after the FGD unit. As illustrated in Table 3, which shows that the NO₂ concentration under typical conditions of a coal-fired boiler was in the range of approximately 4.7–5.7 ppm with a stack diameter of 2.4 m, NO₂ was responsible for less than 0.90% of opacity. Table 4 presents the estimates of parameters K _p and K _w at various loads. For the inversion estimates, the data at various ESP loads produced a K _p of 1.522 cm³/m² and a K _w of 2596 cm³/m², the data at various FGD loads produced a K _p of 1.890 cm³/m² and a K _w of 2347 cm³/m², and the data at various boiler loads produced a K _p of 1.191 cm³/m² and a K _w of 2896 cm³/m². As the mean inversion estimations of a K _w of 1.642 cm³/m² and a K _p of 2520 cm³/m², obtained using all measurements at various loads, are applied to predict the plume opacity, the numerical results reveal that the measured plume opacity data are linearly correlated with the values predicted by Lambert-Beer's law, and the linear regression is 92.94% of confidence.

Table 4. Results of K _p , K _w , k _p, and k _w, estimated from measurements

Parameter	ESP Operation	FGD Operation	Boiler Operation
K p (cm^3/m^2)	1.522	1.890	1.191
Mean K p (cm^3/m^2)		1.642
k p (m^2/g)	0.247	0.199	0.316
Mean k p (m^2/g)		0.229
K w (cm^3/m^2)	2596.1	2346.7	2896.0
Mean K w (cm^3/m^2)		2520.2
k w (m^2/g)	0.000385	0.000426	0.000345
Mean k w (m^2/g)		0.000397
Notes: ρp= 2.66 g/cm^3, ρw = 1.00 g/cm^3.

Theoretical Values of Particle Parameter K _p

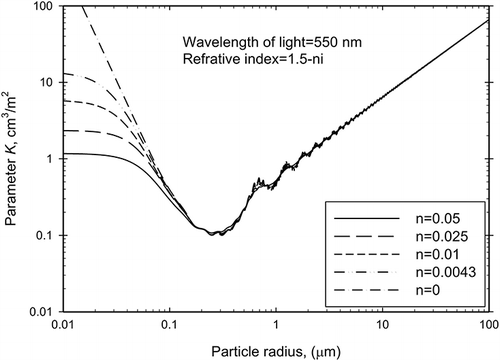
The theoretical particle parameter K _p, computed using eq 12, is determined from the particle number density and the complex refractive index at a given wavelength. The complex refractive index of particles could not be measured directly, and investigations were based on the experimental measurements of transmittance and/or reflectance as well as a corresponding inverse model such as the equivalent spheres model associated with Lorenz-Mie theory or Rayleigh scattering approximation. The optical properties of fly ashes have been studied by various researchers.20,27–30 The real part of the refractive index has been measured in the visible spectral region and was found to vary approximately between 1.5 and 1.6, consistent with results for aluminosilicate glasses in the visible wavelength range. The reported values29 for the imaginary part of the refractive index, ranging up to approximately 0.05, show considerable variations and may vary by more than an order of magnitude for fly ash samples taken from different power plants. Because the real part of the optical constant is similar to that of its major constituents, an average value of 1.5 may be assigned for fly ashes,29–31 whereas the value of the imaginary part ranges from 0 to 0.024 for fly ashes.31 The in situ measurements were made by Gupta and Wall30 at two power stations burning three coals. For these three coals, the values of ash density were found to be 1.78, 1.97, and 2.05 gm/cm³, respectively. It is shown that the unburned carbon has a substantial effect on the absorption index of fly ash particles, with the carbon-free fly ash being characterized by a lower value of the absorption index. After ashing in a muffle furnace, they recommended the refractive index of 1.5-ni, with n ranging from 0.0035 to 0.025 for fly ashes. In the study presented here, fly ash of complex refractive index 1.5-ni, with n ranging from 0 to 0.05 at light wavelength of 550 nm, was used with the BHMIE program. Three samples of particulate matter are considered, and the detailed distributions of particle size and number density are shown over eight size intervals in Table 5. Mean particle size in each interval i was computed, and corresponding K _pi values were calculated at an n of 0.0043, 0.01, and 0.025 with the BHMIE computer program. The results show that the mean theoretical particle parameters, K _p, were 1.334, 1.321, and 1.314 cm³/m², respectively, which are smaller than the measured K _p of 1.642 cm³/m². The corresponding mass extinction coefficients are, respectively, 0.282, 0.285, and 0.286 m²/g, compared with the measured k _p of 0.229 m²/g. The result at an n value of 0.05 is very close to that at an n value of 0.025. Figure 4 also shows the mean value of the theoretical particle parameter K _p over the particle size range of approximately 0.01–100 μm at various values of absorption index. It is illustrated that the effect of absorption index becomes insignificant for particles larger than 0.1 μm at a light wavelength of 550 nm. The discrepancy in experimental and theoretical results of extinction coefficient may be due in part to a deviation of the actual microstructure of the fly ash from the assumed solid spherical structure because fly ash may have formed as spheres that were attached with smaller particles or as hollow spheres that contained solid spheres. The extinction coefficient of hollow spheres is smaller than that of solid spheres; that is, K _p for solid spheres is smaller.32,33

Table 5. Calculated values of the theoretical particle parameter K _p for the measured particle size distribution at various absorption indices

Set	Particle Diameter Size Interval (μm)	Mean Particle Radius (μm)	Mass Fraction Interval (%)	Accumulated Weight Fraction (%)	K pi at m = 1.5, n = 0.0043 (cm^3/m^2)	K pi at m = 1.5, n = 0.01 (cm^3/m^2)	K pi at m = 1.5, n = 0.025 (cm^3/m^2)
	>9.3	10.00	5.11	100.0	6.536	6.413	6.401
	6.0–9.3	3.825	4.69	94.89	2.322	2.344	2.358
	4.1–6.0	2.525	10.82	90.20	1.496	1.477	1.506
	2.8–4.1	1.725	15.31	79.38	1.162	1.095	1.053
	1.8–2.8	1.150	33.06	64.07	0.737	0.708	0.685
1	1.0–1.8	0.700	16.73	31.01	0.527	0.493	0.461
	0.49–1.0	0.373	9.18	14.28	0.115	0.118	0.123
	0.36–0.49	0.213	3.47	5.10	0.119	0.118	0.117
	0.056–0.36	0.104	1.63	1.63	0.410	0.333	0.298
	K p (cm^3/m^2)				1.284	1.252	1.233
	k p (m^2/g)				0.293	0.300	0.305
	>11.0	10.00	10.97	100.0	6.441	6.413	6.401
	7.1–11.0	4.525	3.95	89.03	2.901	2.868	2.829
	4.8–7.1	2.975	8.55	85.08	1.862	1.848	1.827
	3.3–4.8	2.025	14.69	76.53	1.102	1.126	1.165
	2.2–3.3	1.375	29.61	61.84	0.808	0.800	0.794
2	1.1–2.2	0.825	17.54	32.23	0.456	0.454	0.450
	0.59–1.1	0.423	11.18	14.69	0.149	0.150	0.155
	0.44–0.59	0.258	2.19	3.51	0.102	0.103	0.105
	0.056–0.44	0.124	1.32	1.32	0.252	0.243	0.224
	K p (cm^3/m^2)				1.624	1.623	1.629
	k p (m^2/g)				0.231	0.232	0.231
	>9.9	10.00	3.29	99.99	6.447	6.413	6.401
	6.4–9.9	4.075	6.85	96.71	2.568	2.554	2.533
	4.3–6.4	2.675	10.68	89.85	1.559	1.571	1.598
	3.0–4.3	1.825	30.68	79.17	1.172	1.152	1.118
	1.9–3.0	1.225	14.52	48.49	0.810	0.795	0.762
3	1.0–1.9	0.725	14.52	33.97	0.486	0.474	0.452
	0.53–1.0	0.383	12.33	19.45	0.119	0.121	0.127
	0.39–0.53	0.230	3.56	7.12	0.107	0.107	0.108
	0.056–0.39	0.112	3.56	3.56	0.304	0.293	0.265
	K p (cm^3/m^2)				1.095	1.089	1.081
	k p (m^2/g)				0.343	0.345	0.348
Mean	K p (cm^3/m^2)				1.334	1.321	1.314
Mean	k p (1/(ρp K p), m^2/g)				0.282	0.285	0.286

Figure 4. Theoretical parameter K _p as a function of particle size for fly ash at various values of absorption index and a light wavelength of 550 nm.

Comparison of Experimentally Obtained Parameter K _p with Published Values

In Table 6, the measured values of parameters K _p and k _p are compared with previously reported values obtained without considering water-moisture effects. Published values of K _p are lower than 1.642 cm³/m², ranging from 0.60 to 1.20 cm³/m². The value of the extinction coefficient k _p obtained in this study is 0.229 m²/g; published values are larger, ranging from 0.33 to 1.70 m²/g. Discrepancies between the measurements of K _p and k _p obtained here and those made elsewhere are due mainly to the consideration or lack of the effect of water moisture; previously reported measurements do not consider the effect of the extinction by water moisture. It is reasonable that previously reported values of measured k _p are greater than that obtained in this study because they should reflect the effect of extinction by water moisture present in the flue gas. Moreover, the values of particle density listed in the table were all assumed in their calculations, so this might further influence the accuracy of measurements of the parameters k _p and K _p.

Table 6. Comparison of measured K _p values with previously reported values from experiments on coal-fired boilers

Source	Apparatus	Light Path (m)	Parameter k p (m^2/g)	Density ρp (g/cm^3)	Parameter K p (cm^3/m^2)	Reference
Coal power plant (fly ash)	Transmissometer	4.80	0.228	2.66	1.642	This study
Coal power plant (fly ash)	Transmissometer	6.15	∼1.11–1.56	1.00	∼0.683–0.905	9
Coal power plant (fly ash)	Bolometer	1.14	0.78	2.00	0.64	8
Kraft mill recovery furnace	Bolometer	1.52	1.70	1.00	0.60	5
Kraft mill recovery furnace	Smoke meter	0.92	∼0.33–0.50	2.50	∼0.80–1.20	6

Estimation of the Moisture Droplet Mean Diameter

The flue gas had passed through the de-mister with an outlet temperature of nearly 50 °C, where the water content in the flue gas was measured. The mole fraction of water moisture, X _w, in gas was then calculated. Because the theoretical mole fraction of water vapor within the saturated flue gas is denoted as X _wt, the RH is thus determined as the ratio of X _w to X _wt. From Table 3, all averages of the measured RH values of the flue gas in this study are less than 100%; only in a few experimental cases did the variation of the actual water content reach the saturated water content. Specifically, values of average RH ranged from 69 to 98.7%.

For a mass extinction coefficient k _w equal to 0.000397 m²/g, the effective mean diameter, 2r, of the moisture droplets is determined from eqs 13 and 14 to be approximately 13 nm, whereas the mean diameter of a single water molecule is 0.29 nm.

A test was performed to clarify the effect of water moisture on particles and specifically the effect of the absorption of water by particulates. Water was infused into various particle samples, which were obtained at various loads, on filter paper in the ambient environment, and the dissipation of water by spontaneous mass diffusion was measured. It was found that a major loss of water occurred within the first 4 hr; eventually water absorption by the particles was found to be negligible (<5% by weight).

CONCLUSIONS

In this study, two factors that greatly affect opacity were identified: the mass of emitted particles and the amount of water moisture. The effects of SO_x and H₂SO₄ emissions on the opacity of flue gas were negligible because of the range of SO_x concentrations within 20–36 ppm. The opacity was expressed in the form of the Lambert-Beer law, and a nonlinear least-squares regression was conducted to evaluate the two optical parameters K _p and K _w. The measured K _p of 1.642 cm³/m² is larger than the theoretical values of K _p ranging from 1.314 to 1.334 cm³/m² at various values of absorption index. The effect of absorption index becomes insignificant for particles larger than 0.1 μm. The discrepancy in measured extinction coefficient and theoretical values may be because of the fly ash being assumed to have a solid spherical structure, whereas the fly ash may have been formed as spheres that were attached with smaller particles or as hollow spheres that contained solid spheres. Moreover, the obtained K _p value of 1.642 cm³/m² is larger than previously reported values of K _p; that is, the corresponding mass extinction coefficient (k _p = 0.229 m²/g) is smaller than previously reported values of k _p. In previous studies, they did not consider water-moisture effects and assumed a specific value for the particle density, which might further influence the accuracy of inverse estimations of K _p and k _p.

ACKNOWLEDGMENTS

The authors thank the Tuntex Distinct Corporation for financial support and the staff at the coal-fired power plant for their help during the field tests. The authors thank Professor C. J. Tsai at the Institute of Environmental Engineering, Chiao Tung University, for his helpful comments.