Hyperparameter estimation for uncertainty quantification in mesoscale carbon dioxide inversions

Abstract

Uncertainty quantification is critical in the inversion of CO₂ surface fluxes from atmospheric concentration measurements. Here, we estimate the main hyperparameters of the error covariance matrices for a priori fluxes and CO₂ concentrations, that is, the variances and the correlation lengths, using real, continuous hourly CO₂ concentration data in the context of the Ring 2 experiment of the North American Carbon Program Mid Continent Intensive. Several criteria, namely maximum likelihood (ML), general cross-validation (GCV) and χ ² test are compared for the first time under a realistic setting in a mesoscale CO₂ inversion. It is shown that the optimal hyperparameters under the ML criterion assure perfect χ ² consistency of the inverted fluxes. Inversions using the ML error variances estimates rather than the prescribed default values are less weighted by the observations, because the default values underestimate the model-data mismatch error, which is assumed to be dominated by the atmospheric transport error. As for the spatial correlation length in prior flux errors, the Ring 2 network is sparse for GCV, and this method fails to reach an optimum. In contrast, the ML estimate (e.g. an optimum of 20 km for the first week of June 2007) does not support long spatial correlations that are usually assumed in the default values.

• hyperparameter estimation
• uncertainty quantification
• mesoscale carbon dioxide inversions

1. Introduction

The atmosphere integrates the CO₂ source–sink fluxes at all space and time scales to form a spatiotemporal CO₂ field. Consequently, the atmospheric CO₂ mole fraction measurements convey signals from CO₂ fluxes, which can be described by an observation equation:1

To access the supplementary material to this article, please see Supplementary files under Article Tools online.

where x is the spatiotemporal source vector, µ the observation vector, H a linear atmospheric transport operator (Jacobian matrix), and ε _o the signal noise that represents all sorts of uncertainties resulting from the diffusive approximate atmospheric transport and the imperfect measurements. Mathematically, estimating CO₂ fluxes from atmospheric CO₂ concentrations is an ill-posed inverse problem due to the sparsity of the observations and the ill-conditioned Jacobian matrix. Additional information, for example, some prior estimate x ^b of the source, has to be introduced to regularise this inverse problem. Under unbiased and Gaussian assumptions on the errors in this and previous observations, the Bayesian inversion (e.g. Rayner et al., 1999; Bousquet et al., 2000) provides such synthesis by minimising a misfit function:2

where R and B are the covariance matrices for the observation error and the prior flux error, respectively. Together with H, these covariance matrices are determining factors on how information from observation and prior are balanced and assimilated in the inversion (Krakauer et al., 2004; Michalak et al., 2005; Wu et al., 2011).

In CO₂ inversion, these covariance matrices are often parameterised using correlation models that represent our knowledge or hypothesis of the error structure, for example, a distance-decaying model. The parameters of these correlation models, for example, the correlation length and the error variance, are often referred to as hyperparameters.

The Bayesian analysis produces a source synthesis x ^a. Under Gaussian and unbiased assumptions, the misfit function necessarily follows a χ ² distribution with its number of degrees of freedom equal to the number of observations (Tarantola, 2005). In practical CO₂ inversions, the hyperparameters are mostly empirically tuned so that yields a satisfactory χ ² consistency test (Rayner et al., 1999; Rödenbeck et al., 2003; Lauvaux et al., 2012b), except when compensating for unrepresented observation error correlations (Chevallier, 2007).

However, objective estimation of the hyperparameters is a very well-recognised problem in inverse modelling, and there exists classic textbook treatments of this subject (Vogel, 2002; Hansen, 2010). In general, the hyperparameters can be systematically selected to optimise some property of the inversion system. Successful applications can be found for instance in meteorology (Wahba et al., 1995; Dee and da Silva, 1999; Desroziers and Ivanov, 2001) and in inverse modelling of accidental radionuclide release (Davoine and Bocquet, 2007; Winiarek et al., 2012). There are few applications of hyperparameter estimation in global CO₂ inversion under the criteria of maximum likelihood (ML, Michalak et al., 2005) or general cross-validation (GCV, Krakauer et al., 2004). In this article, we present a first attempt at applying hyperparameter estimation in more complex mesoscale CO₂ inversions using real, continuous hourly CO₂ concentration data in the context of the Ring 2 experiment of the North American Carbon Program Mid Continent Intensive (MCI, Miles et al., 2012). For the first time, different criteria, namely ML, GCV and χ ² test, are investigated in the same setting of mesoscale inversion to explore the replacement of empirical tuning, at least partially, with hyperparameter estimation for uncertainty quantification in practical CO₂ inversions.

We describe the inversion system and the hyperparameter estimation methods in Section 2. The experiment set-up is summarised in Section 3. Section 4 presents the estimation results. In Section 5, we discuss the method performance and draw conclusions. A detailed formulation of all three estimation criteria is given in Appendix A.

2. Methodology

2.1. Analytical Bayesian inversion

For a given spatiotemporal domain at mesoscale, the full parameter vector x can be composed of three parts: the spatiotemporal surface flux f, the concentration β at domain spatial boundaries, and the concentration γ at the initial time. Let us detail the Jacobian matrix for f, β and γ as , the observational equation (1) becomes:3

If we group the influence of the boundary and initial concentrations (β and γ) at tower sites into a background concentration vector , the observational equation is then:4

In this article, β and γ are taken from CarbonTracker products corrected by aircraft data (Lauvaux et al., 2012b). Their influence µ _BG is simulated with the WRF-Chem atmospheric transport. These background concentrations are then removed from the tower measurements for the inversion of surface CO₂ fluxes. The synoptic spatial structures of the boundary concentrations have much larger scales than those of the regional fluxes. Therefore, it would be reasonable to expect that the boundary influence on the spatial structure of the flux errors is insignificant. Consequently, we exclude β and γ from our inversions for the estimation of hyperparameters. In the following, the source vector x is replaced by f to make explicit this simplification.

If we assume that the errors in the prior fluxes and the observations are Gaussian (with covariance matrix B and R, respectively) and independent, the analytical Bayesian inversion can be formulated as a BLUE (best linear unbiased estimator) analysis:5

where K is the gain matrix6

and f ^a is the vector of inverted fluxes. After inversion, we have a refined estimate error ε _a=f ^a−f with its covariance matrix equal to:7

where I _n is the identity matrix in ℝ.

We parameterise the prior error covariance matrix B using the isotropic Balgovind correlation model (Balgovind et al., 1983). The prior error covariance between two spatial points s ₁ and s ₂ is computed by:8

where L is the characteristic correlation length, h=s₁−s₂ is the spatial distance, and σ _b is the background error standard deviation (sd). In this study, both L and σ _b are assumed to be homogeneous. In future studies, we will test heterogeneous L and σ _b values taking into account the non-stationary impact of local ecosystems. The correlation in the parameterised B smoothes and spreads the information from the model-observation mismatch d= µ −Hf ^b (also called the innovation vector).

The spatial correlations in hourly observation errors are known to be rather short with a correlation length of 30–40 km (Lauvaux et al., 2009). Such very short correlation length can also be found in Gerbig et al. (2003). The closest pair of towers in the Ring 2 network is separated by 120 km. Consequently, no spatial correlation is considered in R in this study. However, we use a temporal Balgovind correlation model with the characteristic correlation length set to 1 hour that fits our previous empirical configuration (Lauvaux et al., 2012b). We denote by σ _o the observation error sd.

2.2. Hyperparameter estimation

Let be the vector of hyperparameters. The terrain of the domain of the Ring 2 experiment is flat and abundant with crops. The error sd σ _o, σ _b and the prior error correlation length L are assumed to be homogeneously distributed within the cropland. The hyperparameter estimation problem is to determine θ so that a given criterion is optimal. In this section, we briefly discuss three different criteria: χ ² test, ML estimation and GCV. For completeness, we formulate the algorithmic details of all the three criteria in Appendix A.

Under Gaussian and unbiased assumptions, the innovation vector d follows a Gaussian law: , where is its covariance matrix. One can thus tune θ so that the covariance matrix is consistent with the actual innovation statistics: (Ménard and Chang, 2000; Desroziers et al., 2005). E is the expectation operator. In fact, this is equivalent to the χ ² consistency test noting that the misfit function at the minimum can be evaluated by (Tarantola, 2005).

Let be the probability density function (pdf) of the innovation vector conditioned by θ . Given the actual innovation d, the ML estimate of θ is another way to determine the hyperparameter (Dee and da Silva, 1999; Michalak et al., 2005). We select θ that maximises the innovation pdf9

that is, the Gaussian law most likely generates the observed innovation vector. The ML estimation problem can be solved using the Desroziers scheme (an iterative fixed-point algorithm (Desroziers and Ivanov, 2001)). It is easy to show that, by construction, the Desroziers scheme generates perfect χ ² distribution for the misfit function in eq. (2) (Michalak et al., 2005; Koohkan and Bocquet, 2012). The ML estimation problem (9) can also be solved using numerical optimisation algorithms. The uncertainty of the ML estimates of the hyperparameters can be assessed by the second derivatives of the negative logarithm likelihood function.

The GCV hyperparameter estimation aims at selecting a best inversion set-up within a family of all possible inverted sources parameterised by θ so that the mean-square error of the concentration predictions (pmse) is minimised. GCV is an asymptotic case of leave-one-out cross-validation, in which averaged contribution of all observations to the inversion is used instead of taking each specific observation into account. It is a well-developed statistical tool for environmental inverse modelling (Wahba et al., 1995; Dee and da Silva, 1999), especially appropriate when observations are abundant or the impact of observations is homogeneous. It has been applied in CO₂ hyperparameter estimation with diagonal covariance matrices (Krakauer et al., 2004). However, there are very few such investigations for the case of correlated covariance estimation. Note that for a given L, the optimal σ _o and σ _b values, which are obtained by the Desroziers scheme (i.e. the ML estimates) and assure perfect χ ² test, also minimise the GCV pmse (Desroziers and Ivanov, 2001).

2.3. An indicator of the inversion system

The number of degrees of freedom for the signal (DFS) is the expectation of the prior part of the misfit function in eq. (2) at the minimum: . It measures the information gain from observations used to resolve fluxes (Rodgers, 2000). In other words, it accounts for the weight assigned to the observations by the inversion system. The correlation length L has a great impact on DFS. For longer L, the inversion is mainly constrained by the prior fluxes, therefore a smaller DFS value is expected. The number of DFS is an indicator that measures how effective the observations are for the inversion, but it is not a criterion for hyperparameter estimation.

3. Experiment set-up

We use daytime measurements of the CO₂ dry air mole fraction from eight tower sites of the Ring 2 experiment. Two towers are part of the permanent tall tower NOAA network, LEF and WBI; five sites were instrumented for the campaign, Kewanee, Round Lake, Mead, Galesville, Centerville; and the last site is the calibrated flux tower Missouri Ozarks (see Fig. 1a in Lauvaux et al., 2012a). The mole fraction observations at nighttime are excluded from our inversions due to the unsatisfactory modelling of atmospheric transport within the boundary layer at night. For weekly inversions, the number of observations d ranges from several hundreds to 1000, which makes an analytical Bayesian inversion feasible.

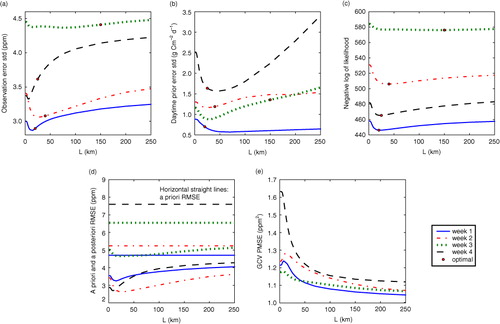
Fig. 1 Hyperparameter estimation results using the Desroziers scheme. The estimations are conducted respectively for 4 weeks of June in 2007 with different correlation lengths Ls listed in the x-axis. We show the resulting hyperparameters: (a) optimal standard deviation (sd) of observation errors; (b) optimal sd of daytime prior flux errors. The criteria evaluated for these optimal hyperparameters are: (c) negative logarithm of the likelihood computed with optimal hyperparameters; (d) the root mean-square error (rmse) for the CO₂ mole fraction simulations at all towers using a priori and a posteriori CO₂ surface fluxes; (e) the GCV predictive mean-square error (pmse). The optimal correlation lengths bearing maximum likelihoods and the corresponding optimal sds are marked out by the circles in (a), (b) and (c).

Weekly mean CO₂ fluxes (day and night) are inverted at 20-km resolution over a domain of size 980 km×980 km (see Fig. 2a). The dimension of the weekly flux vector f on the 49×49 surface grid is thus n=49×49×2 = 4802.

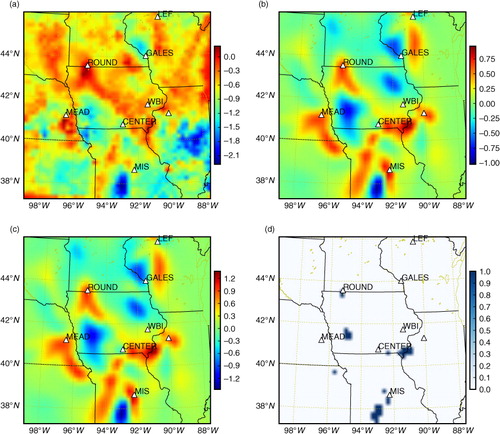
Fig. 2 Inversion results with the optimal hyperparameter σ _o, σ _b and L (20 km) under the maximum likelihood (ML) criterion for the first week of June in 2007. The fluxes are in g C m⁻² d⁻¹. (a) Daytime inverted surface fluxes; (b) correction of the daytime inverted fluxes against the prior SiBcrop fluxes; (c) flux corrections of (b) normalised by σ _b; (d) regions where the flux corrections of (b) are within one-sigma (indexed by 0) or out of one-sigma but within two-sigma (indexed by one).

The WRF-Chem meteorological fields at 10-km resolution are used to drive the Lagrangian Particle Dispersion Model (LPDM, Uliasz, 1994). Each row of the Jacobian matrix H is computed by the density of the LPDM particles emitted from towers and transported backward, accounting for the contribution of the sources on the corresponding concentration observation. The prior weekly mean fluxes are obtained from the SiBcrop model simulations, with an improved phenology for crops based on several eddy-flux sites over the MCI (Lokupitiya et al., 2009).

4. Results

4.1. ML estimation and χ ² test

4.1.1. Optimal hyperparameters

We perform ML estimation of the hyperparameters σ _o and σ _b using the Desroziers scheme with L ranging from 1 to 250 km for the 4 weeks of June in 2007. These optimal σ _o and σ _b are thus specific of a given L. We impose a fixed ratio between the nighttime and daytime prior error sds. This ratio is set according to the ratio between the ranges of flux variations at day and night. The optimal σ _o figures (Fig. 1a) are close to the default values (3–5 ppm in summer) obtained by diagnosing the atmospheric transport error due to incorrect vertical mixing, flux aggregations and the misrepresentation of Eulerian dynamics by the Lagrangian model (Lauvaux et al., 2012b). In contrast, the optimal daytime σ _b figures (Fig. 1b) are far smaller than the default value (10 g C m⁻² d⁻¹ (Lauvaux et al., 2012b)). The resulting large σ _o/σ _b ratios imply that the inversions using optimal error variances are less constrained by the observations than the default case.

With the default error variances, the atmospheric transport error is underestimated. For instance, the vertical transport errors may be insufficiently accounted for or the prescribed spatiotemporal covariance structure may not well represent the correlations in the errors of the continuous hourly observations for the Ring 2 experiment. In midsummer, this area experiences very strong storms, and during dry season, two severe droughts affected some parts of the Midwest in August. The WRF convective scheme may have difficulty simulating these events correctly, which results in large transport errors. Detailed diagnostics of the transport error is in process using WRF multi-physics ensembles compared with observations (e.g. radio-sounding and surface data). This is an important related subject but beyond the scope of this article.

For each Balgovind correlation length L, we verified that the ML estimate of σ _o and σ _b (Fig. 1a and b) assures perfect χ ² test. We omit the χ ² curves that all approach 1. Note that, in many studies, the covariance hyperparameters are empirically tuned for satisfactory χ ² tests.

The ML estimate of L defines the most plausible prior error covariance that adapts to the innovation sample under the assumption of isotropic Balgovind correlation in prior flux errors. Most optimal L values (read the minimal negative logarithm likelihoods in Fig. 1c) are rather short: between 20 and 45 km. There is one exceptionally long optimal L of 150 km for the third week of June, for which the observation error increase is the strongest (largest σ _o/σ _b ratio read from Fig. 1a and b). In this case, the signal from the surface fluxes is highly affected by the atmospheric transport error, so that it is difficult to retrieve meaningful spatial prior correlation structure. The corresponding negative likelihood curve in Fig. 1c is plainly flat with very small curvature at the ML estimate. The ML estimation in this case is highly uncertain.

To quantitatively account for the uncertainty of the ML estimates, we compute the second derivatives of the negative logarithm likelihood function and construct its Hessian matrix. The inverse of that Hessian matrix provides an approximation of the covariance matrix for the ML estimate (see Appendix B for algorithmic details). We list the standard deviations for the ML estimates in Table 1. In summary, the ML estimation does not support long spatial correlations in prior flux errors that are usually assumed, for example, 300 km in Lauvaux et al. (2012a). This result confirms the global prior error estimation results obtained by objective statistics of the differences between CO₂ flux observations and flux simulations using a terrestrial ecosystem model (Chevallier et al., 2012).

Table 1. Values and standard deviations of the ML estimates for the observation error sd σ _o in ppm, the daytime flux error sd σ _b in g C m⁻² d⁻¹, and the Balgovind prior error correlation length L in kilometres

	σ o	Daytime σ b	σ b L
Week 1	2.89±0.149	3.21±1.13	20±6.77
Week 2	3.08±0.181	5.45±1.99	40±13.6
Week 3	–	–	–
Week 4	3.62±0.241	7.51±3.48	25±7.90

For week 3, the flat negative likelihood curve results in an ill-conditioned and non-positive Hessian matrix, which prevents direct computation of the sd of ML estimates.

We preliminarily assess the robustness of our estimates of L using a longer temporal correlation length of 2 hours (default 1 hour) for R. The resulting new optimal L is 50 km with high uncertainty (also a flat, negative log likelihood curve in Supplementary file). Other error covariance structures could also be possible.

In addition to the Desroziers method, we also tested other iterative methods that adopt non-linear optimisation algorithms (either gradient-based or gradient-free) to solve the ML estimation problem numerically. We found that, in most cases, they provide estimates consistent with those obtained using the Desroziers method but occasionally get trapped into local optima for the estimation of L given certain initial parameter values (results omitted). Therefore, it is desirable to perform the Desroziers method for different L values enumerated ranging from 1 to 250 km.

4.1.2. Inversions using optimal hyperparameters

We perform inversions using all the L-specific optimal σ _o and σ _b values. The short optimal correlation length (e.g. L = 20 km for the first week of June) prevents the information to propagate far from the towers within the flux domain through the inversion (see the daytime flux corrections in Fig. 2b). In Fig. 1d, we show the root mean-square error (rmse) for the CO₂ mole fraction simulations averaged over all towers using prior and inverted CO₂ surface fluxes. The a posteriori rmses are substantially improved compared with the a priori rmses. Localising the observation impact (short optimal Ls) is beneficial to inversion in terms of rmse reduction for the dependent data.

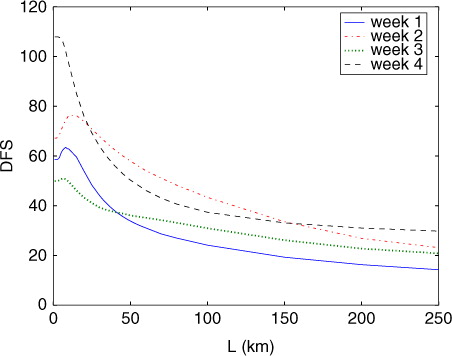
The inverted fluxes obtained using the optimal short L and corresponding optimal σ _o and σ _b are physically relevant (e.g. no significant positive fluxes at daytime in Fig. 2a). Using a long L (e.g. 200 km) and its corresponding optimal σ _o and σ _b (therefore perfect χ ² test) often leads to unrealistic inverted fluxes. For instance, for the case of week 3, we observed very positive daytime inverted fluxes, and for the cases of weeks 2 and 4, we observed many negative nighttime inverted fluxes (figures omitted). Moreover, Lauvaux et al. (2012a) have performed the leave-one-tower-out cross-validation for long L and found almost no gain in concentration rmse at validation towers. In addition, long L values lead to poor information gain from the observations, and as such with smaller DFS values (Fig. 3).

Fig. 3 Numbers of DFS with respect to correlation length L in prior flux errors for 4 weeks of June in 2007. Inversions are performed using optimal hyperparameters obtained by the Desroziers scheme. X-axis lists different correlation length Ls.

We also compute the total regional a priori error budgets and compare them with the total regional flux corrections by the inversions using the optimal hyperparameters for the 4 weeks of June in 2007. Here, the regional a priori error budget – the total flux uncertainty – is computed by , where B _ij is the entry of B in row i and column j, and a is the multiplicator converting the fluxes into the error budgets. We confirm that all the 4 weekly flux corrections are within the regional error budget (Table 2). In Fig. 2, we show the inversion results using optimal hyperparameter values for the first week of June in 2007. It can be seen that most flux corrections are within the one-sigma range (Fig. 2c and d): the inversion system with the optimal hyperparameter values is statistically consistent.

Table 2. Comparison between the total regional error budget of a priori fluxes (‘budget’ column) and the total regional flux correction by inversions (‘correction’ column) for the 4 weeks of June in 2007

	Optimal L (km)	Budget (Gg C)	Correction (Gg C)
week 1	20	227	201
week 2	40	742	601
week 3	150	2546	674
week 4	25	658	621

The optimal hyperparameters obtained by the Desroziers method (marked out by the circles in Fig. 1a and b) are used for this comparison.

We do not extend this evaluation to longer time scales, for example, the month or the year, since we perform weekly inversions without the possibility to correlate errors from 1 week to the next, even though there is some evidence that such long correlations exist (Chevallier et al., 2012): neglecting temporal correlations leads to underestimating the a priori error budgets for periods longer than a week.

4.2. General cross-validation

Krakauer et al. (2004) reported a successful application of GCV in global CO₂ hyperparameter estimation for the case of diagonal covariance matrices; however, the effectiveness of GCV for the case of correlated covariance matrices is still unknown. Recall that for a given L, the GCV estimate of σ _o and σ _b coincides with the ML estimate. Consequently, we use the ML estimate of σ _o and σ _b to compute the GCV pmses for different Ls values. It is seen that GCV fails to find an optimal L (Fig. 1e). We can see two possible reasons for this failure: (1) GCV is a criterion of approximate leave-one-out cross-validation based on the assumption of a uniform impact of the observations, but the Ring 2 network is spatially too sparse and too heterogeneous for such approximation; (2) GCV is very sensitive to the error structure in R (Wahba et al., 1995) but in our case R is empirically determined.

5. Discussion and conclusions

Direct approaches to quantify the uncertainty of prior fluxes are based on the statistics of flux misfits. For instance, Rödenbeck et al. (2003) intercompared several terrestrial and ocean models, and Chevallier et al. (2006, 2012) compared ecosystem model simulations with eddy-covariance flux measurements. These statistics only partially explore the space of uncertainties, because this space can be sampled by few models in the former case and by few measurements in the latter one. Additional information is needed to verify and complement the direct approaches. The proposed hyperparameter estimation methodology is one such effort that analyses the signal from mole fraction measurements to estimate the flux uncertainty. To put it more generally, this methodology selects the uncertainty hyperparameters that optimise some desired property of the inversion system, like maximising the likelihood of observation (ML), the χ ² consistency under the Gaussian paradigm, and GCV of inverted fluxes. This approach also benefits the assignment of observation error statistics: observation error statistics account for the errors of the underlying transport model, of which estimation has been another long-standing issue (e.g. Gurney et al., 2002). The computational cost of optimising the inversion system is of one order of magnitude larger than that of the inversion and has hampered such developments so far.

We have examined the ML estimation, the χ ² test and the GCV in estimating the variances and the correlation lengths of the error covariance matrices for prior fluxes and concentration observations in a mesoscale setting. Real, continuous hourly CO₂ concentration data were assimilated to invert weekly CO₂ fluxes at a 20-km resolution.

The correlation length L characterises the errors in the modelling of the ecophysiological processes that generate the fluxes. Its estimation based on CO₂ mole fraction measurements only may not always be appropriate. In this article, we have enumerated different L values, and for each L value an ML estimation is conducted. We interpret these results with great caution.

For a given correlation length L in prior flux errors, the ML and GCV estimates of the error variances coincide and assure perfect χ ² test. In addition, the misspecifications of default observation error variance values were corrected to represent the atmospheric transport error. When L was to be estimated jointly with the error variances, the ML estimate did not support long spatial correlations (e.g. an optimum of 20 km for the first week of June 2007), which is consistent with the estimation results at the global scale obtained in the direct approach (Chevallier et al., 2012). In contrast, GCV failed to provide optimal L values. In the same geophysical data-sparse context, Bocquet (2012) also found the ML estimation superior to GCV for the inverse modelling of radionuclide release. We further diagnosed the flux error budget and the flux corrections by the inversions using optimal hyperparameters. The optimised inversions produced satisfactory statistical consistency, in spite of the limitations of the Gaussian modelling framework (that may be less valid for mesoscale regional inversions than for global ones).

We have evaluated the robustness of our study by conducting hyperparameter estimation for other periods in the summer of 2007. The results show consistent patterns (see Supplementary file): (1) GCV fails to estimate L, and the ML estimate does not support long L; and (2) when the atmospheric transport error is significant, it is difficult to identify a meaningful optimal L from the flat likelihood curve.

The hyperparameter estimation appears to be a promising alternative to empirical tuning methods for uncertainty quantification. In principle, its computational load dramatically increases with the observation number, if the huge covariance matrices have to be evaluated. However, hyperparameter estimation in such a situation should not be considered to be a daunting task. Randomisation techniques exist to avoid huge matrix computations using perturbed variational inversions, and the ML estimation could be done with few iterations. Both have already been successfully demonstrated in meteorological applications (Desroziers and Ivanov, 2001; Chapnik et al., 2004).

The boundary and initial concentrations have been corrected by aircraft data to decrease the bias of the system. Removing the remaining bias leads to maximal 10% relative differences in inverted fluxes near the towers. Hence, the potential bias has very limited impact on our weekly inversions. For longer periods, such bias will play a more important role on the estimation of the regional budget and should be estimated jointly with the fluxes. By imposing longer spatial correlations in flux errors for inversions, the distribution of the flux corrections at finer spatial scales may be less precise; however, jointly with bias corrections, the regional budget can be satisfactorily estimated (Schuh et al., 2013).

Careful attention and further investigations are needed for the full-scale mesoscale application of hyperparameter estimation. The space–time density of the observation network may limit the estimation of some hyperparameters, like L, due to insufficient statistics. In our case, a denser network than the one studied here would be helpful for more robust estimates. To mitigate the effect of a sparse network, some reliable knowledge about the hyperparameters may be necessary, especially when many hyperparameters are to be estimated. For instance, in our study, we used information from model simulations to impose the initial and lateral boundary conditions and the ratio between daytime and nighttime flux error variances rather than estimating them. However, when such hypotheses are not reasonable, the hyperparameter estimation may yield misleading results. Data density is also desirable to leave some mole fraction measurements out of the estimation process for the validation of the optimised hyperparameters. Direct flux observations can also serve for this purpose.

6. Acknowledgements

This study is a contribution to the MSDAG project supported by the French Agence Nationale de la Recherche grant ANR-08-SYSC-014. The first author is currently funded by the industrial chaire BridGES supported by the Université de Versailles Saint-Quentin-en-Yvelines, the Commissariat à l’Énergie Atomique et aux Énergies Renouvelables, the Centre National de la Recherche Scientifique, Thales Alenia Space and Veolia.

7. Appendix

A. Criteria for hyperparameter estimation

Suppose the surface CO₂ flux vector ℝ ⁿ can be related to the observation (or receptor) vector ℝ ^d as:A1

where ε _o is an error vector with zero mean, and H is a linear operator that includes the atmospheric transport.

The Bayesian inversion specifies the a posteriori probability density function (pdf) given information on the prior and the observation according to Bayes’ rule:A2

where is the probability density of a sample.

In CO₂ inversions, the prior estimate of f is usually assumed to follow a Gaussian law :A3

where f ^b is a prior guess vector, and is the covariance matrix for the unbiased prior error . Here, the expectation operator is denoted by E. The Gaussian assumption is convenient for the computation of the likelihood of observations given fluxes:A4

where is the observation error covariance matrix.

Let be the vector of hyperparameters. The objective of the hyperparameter estimation problem is to find θ so that a given criterion J( θ ) is optimal for the estimation of the surface fluxes f.

A1. Maximum likelihood estimation

In the ML hyperparameter estimation, one chooses θ that maximises its conditional pdf . If we assume a constant evidence p( µ ) (a normalising denominator) and a uniform prior p( θ ) (no available prior information on θ ), according to Bayes’ rule:A5

the posterior is proportional to the likelihood :A6

The maximum likelihood estimation problem is then:A7

When reaches its maximum at θ *, the pdf is the most peaked, which indicates that the observation µ is the least uncertain.

In the context of analytical Bayesian inversion, the likelihood can be further evaluated byA8

where is the covariance matrix of the innovation vector . The corresponding negative logarithm likelihood to be minimised is:A9

where C is an irrelevant constant.

For a given L, supposing the true error covariance matrices are of the forms B ^t =s ^b B and R ^t =s°R where B and R are computed using fixed default σ _o and σ _b, the hyperparameter vector then becomes θ =[s°, s ^b]^T. The Desroziers scheme (Desroziers and Ivanov, 2001) can be used to iteratively solve the necessary condition (zero-gradient) of the maximum likelihood estimation problemA10

as follows:A11 A12

whereA13 A14 A15

Provided s ^a and s ^b are of the same order of magnitude (i.e. the default σ _o and σ _b are not far from the true values), the Hessian matrix of the negative log likelihood function equation (A9) has positive diagonal terms and negligible non-diagonal terms (Chapnik et al., 2004). This assures us that the Desroziers scheme reaches one minimum of the negative log likelihood function. There exists efficient randomisation algorithms to compute the trace terms in eqs. (A11) and (A12) for very large observation sets (Desroziers and Ivanov, 2001). This is a typical configuration in variational CO₂ inversions (Chevallier et al., 2010), for which it is computationally infeasible to use the original maximum likelihood formalism equation (A9) for hyperparameter estimation. Furthermore, the Desroziers scheme could terminate with satisfactory solutions in a few iterations (Chapnik et al., 2004).

In general, the different sources of uncertainties are entangled in the inversion system, which complicates the uncertainty quantification problem. If R and B have equal correlation length in the observation space (HBH ^T=α R with 0 < α∈ℝ), then eqs. (A11) and (A12) are identical. In this case, the Desroziers scheme fails to provide a solution (Chapnik et al., 2004). In our study, since R is taken to be spatially uncorrelated, R and HBH ^T have distinct correlation structures, which favours the identification of the error variances.

The Desroziers scheme stems from the consistency check of the inversion system by statistical diagnosis of the inverted variables, for example, . The term J _b(f ^a) is a satisfactory approximation of its expected value E[J _b(f ^a)], if the time window for inversions is long enough to include a large batch of observations for sufficient statistics. This approximation implies an ergodicity assumption for the retrieval of the desired knowledge (the hyperparameter values in our case) from the statistics of one single realisation of the underlying geophysical process. Similarly, the negative log likelihood function relies also on one realisation of µ and f _b. The hyperparameter estimation is thus data specific; however, it is reasonable to expect that the estimation results are robust for similar scenarios, for example, summer time weekly inversions.

Other iterative methods exist to numerically minimise the negative log likelihood function equation (A9). These numerical optimisation methods can be either gradient-based (e.g. the augmented Lagrangian method) or gradient-free (e.g. constrained optimisation by linear approximations). In this study, we used the NLopt library (http://ab-initio.mit.edu/nlopt) for non-linear optimisation.

A2. Degrees of freedom for the signal and χ ²

The number of degrees of freedom for the signal (DFS) can be defined as (Rodgers, 2000):A16

where E is the expectation operator over the errors in the prior fluxes and the observations. The DFS measure the relative correction of f ^a to f ^b. Under Gaussian assumptions, the DFS can be computed by where is the averaging kernel matrix. This equals to , which measures the relative reduction of uncertainty for the BLUE analysis.

It is well known that if the Gaussian assumptions on prior and observation errors are valid, the quantityA17

follows a χ ² probability density of which the number of degrees of freedom equals the number of the observation d. Rayner et al. (1999), Rödenbeck et al. (2003), Lauvaux et al. (2012b) empirically selected the hyperparameter values by checking the χ ² consistency of f ^a.

For the Desroziers scheme using one single realisation of a batch of observations, by eqs. (A11), (A12), (A14), (A15), we haveA18

This means that the parameter θ * obtained using the Desroziers scheme bears the perfect χ ² test for that batch of data (see Koohkan and Bocquet, 2012 for a direct fixed-point method that leads to the perfect χ ² test).

A3. Cross-validation

An ideal criterion accounting for the inversion performance is the predictive mean-square error (pmse):A19

where f is the assumed true flux vector and f ^a is the inverted flux vector using hyperparameter θ . This criterion is not practical since f is unknown. However, other criteria can be derived when f is replaced by f ^a but the expectation remains the least affected. The general cross-validation (GCV) pmse is one such criterion.

One popular cross-validation criterion is the leave-one-out cross-validation error:A20

Here is the inverted flux vector using d−1 observations with the i-th observation µ _i removed from inversion, and H _i the i-th row of H associated with µ _i . The computation of Q( θ ) is time consuming since d times of inversion are needed. Using the ordinary cross-validation (OCV) identity (Wahba, 1990), this could be reduced to only one time of inversion by replacing Q( θ ) withA21

where the matrix HK _θ is the resolution matrix (Rodgers, 2000) with its i-th diagonal element indicating the number of DFS elucidated by assimilating i-th observation µ _i Unfortunately, Q′( θ ) has a disturbing dependence on the ordering of the observations ( changes if the rows of H are permuted).

The GCV pmseA22

is an approximation of Q′( θ ), in which the averaged contribution of all observations to inversion is used instead of the specific observation contribution so that some ordering invariance properties could be achieved. GCV has the property that its expectation is close to that of P( θ ). Note that we have formulated V( θ ) in R ⁻¹-norm. In this case, the scaled observational error is expected to be white, which would favour the separation of noise from signal for GCV hyperparameter estimation. Nevertheless, if the covariance structure of R is unrealistic, the scaled observation error would not be white. This may significantly degrade the GCV performance (Wahba et al., 1995).

For a given L, the hyperparameters s ^o and s ^b obtained using the Desroziers scheme minimise the GCV pmse (Desroziers and Ivanov, 2001).

B. Uncertainty of the hyperparameter estimates

The ML estimate θ * has several desired properties in the asymptotic limit of very large samples. For instance, the distribution of θ * approaches normality, and the covariance of this normal distribution can be approximately computed by the inverse of the Hessian matrix (the second partial derivatives) of the negative log likelihood function equation (A9) at the ML estimate θ *. We refer to statistics texts (for instance Efron and Hinkley, 1978; Lindsey, 1996) for more details.

In geophysical applications, it would be demanding for large samples, since the underlying phenomena are so complex that an observation never repeats under identical conditions. However, it is still possible to perform parameter estimation for a single sample of one realisation of the geophysical process (Dee, 1995). This would result in covariance models more consistent with the actual innovations. For reliable accuracy, Dee and da Silva (1999) suggest that an order of 100 observations is required to estimate a single parameter. In our study, more observations are available than required by this empirical rule.

Let us formulate explicitly the ij-th element of the Hessian matrix of the negative log likelihood function equation (A9) as:B1

By linear algebra and matrix calculus, we haveB2

whereB3 B4

are the first and second derivatives of the innovation covariance matrix D _θ .

The Hessian matrix at the ML estimate θ * has a geometric interpretation. It characterises the local curvature of the negative log likelihood function. The magnitude of a change in resulting from a perturbation of θ * along the eigen-direction of is proportional to the corresponding eigenvalue. Therefore, the Hessian matrix is related to the accuracy of the ML estimate. The approximate covariance matrix for the ML estimate is simply the inverse of the Hessian matrix at θ *B5

The small curvature (at the ML estimate) of the flat negative log likelihood curve for week 3 in June 2007 in Fig. 1c indicates that the estimation is inaccurate and bears large uncertainties. The corresponding Hessian matrix could be ill-conditioned and non-positive definite. In this case, higher order moments may be needed to clarify these large uncertainties.

The negative log likelihood function in eq. (A9) is correct only under Gaussian assumptions with known covariance structures. When these assumptions do not hold, solutions from minimising eq. (A9) will not be guaranteed to be the ML estimates, but result in parametric covariance models that are more consistent with data. To account for uncertainties due to the unknown covariance structure, that is the robustness of the estimates, one can perform a sensitivity analysis for the parameter estimation problem under different assumptions. For instance, correlation models other than Balgovind could be tested; the background error covariance matrix B _θ could be anisotropic; and the structure of the observation error covariance matrix R _θ may take on more realistic forms. Detailed analysis on robustness would be beyond the scope of this article but we will keep in mind for future studies.