A brief review of mathematical models of thin film growth and surfaces

Abstract

The morphology of thin films has been extensively studied in the last years. The properties of a thin film are closely related to its microstructure, especially to its morphology and surface roughness. Optical reflectivity, conductivity, and porosity are characteristics that depend on the film structure. The knowledge of atomistic details of the thin film growth process is useful for the development of new techniques and the control of thin films and new materials. Models of growth process are very powerful tools that can help researchers to predict and control physical, chemical, and mechanical properties. In this work we briefly summarize the theoretical models that have been used in the studies of thin films growth. By describing the deposition process of atoms/molecules on the surface of the substrate, one can study the evolution of the bulk and the surface roughness of a thin film. If an experimental growth process is appropriately described by a theoretical model (or even a combination of one or more different models), it can also provide indications to control the surface roughness and porosity of the film. Controlling the growth process one can obtain materials with a set of desired properties, namely tribological, porosity, and electrical ones. These characteristics are necessary for example, for hosting a solid lubricant on the surface of the material. We believe that the models presented in this work can be very useful in understanding the mechanisms of control and adherence of electrodeposited films which are commonly used in medical applications such as stent devices. We also believe that the models can be helpful to the understanding surface problems related to the superficial defects in stents.

Keywords: :

• mathematical modeling
• surface growth
• thin films
• surface roughness
• porosity
• stent devices

Introduction

The formation of thin films due to the deposition of particles on a substrate allows the development of materials with important technological applications. By controlling the surface properties, one can control the properties of the material by shaping the surfaces with desired purposes. The study of the surface growth and its evolution allows the researcher to focus the investigation on the important parameters that determine the morphology skipping the unnecessary details. This task is usually accomplished through the use of mathematical models, which simulate the growth of a thin film determining its thickness, surface roughness, and porosity in the bulk.

Advanced studies in recent years allowed a deeper understanding of the fundamental phenomena which govern the deposition of atoms or particles forming a thin film at nanoscale. The theoretical and computational models presented herein represent a powerful tool to study the growth of thin films and interfaces. Many models are quite simple due to the simple phenomena being modeled. On the other hand some of the models have very simple features and therefore deviate from the real deposition and growth of the film. Nevertheless these models can be seen as a good starting point for obtaining more accurate ones by adding ingredients in the model that are directly related to the experimental growth process. It is usually necessary to combine different models (or even characteristics of a model) to get a better approximation of the experimental conditions.

New experimental techniques, such as sputtering or Molecular Beam Epitaxy (MBE), can provide suitable materials for medical applications. Thin and ultra-thin film coatings for stent devices are, perhaps, one of most remarkable examples of nanostructured biomaterials applied in medicine. From the theoretical point of view, physicists can apply the well-known tools of statistical mechanics along the computational techniques to describe new phenomena and provide understanding for these new materials.

In this work we present a brief introduction of theoretical concepts related to the surface growth and interface evolutions and the most common models used in simulations. After presenting the main theoretical concepts for mathematical modeling of a surface growth, some applications will be analyzed in real cases, comparing the results obtained by simulations with those obtained experimentally.

Theoretical Concepts

By adopting mathematical models as a tool to describe the deposition of a film, it is necessary to use some theoretical concepts that allow the description of this process. The surface roughness, the fractal dimension of a surface, the height of a given position in the substrate, the porosity of the bulk in the film, and how these quantities may vary with time are the principal properties related to a film growth process and, in many cases, they are interdependent.

Parameters of a growing surface

One can describe the height h(i,t) of a given position i on the surface as a function of time. To describe qualitatively the growth of the surface, it is necessary to look at the mean height of the interface:¹

(1)

where L is the linear size of the network and d the dimensionality of the system. The surface roughness is defined by the width of the formed interface, as the mean square fluctuation of the height. The roughness is a function of the linear size of the system and of the time:

(2)

The surface roughness evolves in time with two distinct regimes depending on the type of film growth. At early stages of the deposition process, the roughness grows with time, following a power law.

For the initial times, one can describe the roughness as a power law in the form:

(3)

The exponent β is called “growth exponent,” since characterizes the growth features of a surface and the term t_x is defined as “crossover time,” representing the time required to change the growing regime. After the crossover time t_x, this regime may turn into a new one, called saturation regime, in which the roughness reaches a saturation value and does not change in time. For the saturation regime the surface width increases as L increases, in the form:

(4)

where α is the “roughness exponent.” This exponent shows that the saturation of the roughness is not a local effect and can grow indefinitely for L → infinity.

There are few processes in which the surface roughness does not saturate and grows indefinitely with time. This characteristic is due to the random processes and uncorrelated growth of the surface. This process is called random deposition and may describe a physicochemical process, such as the atomic layer deposition.²

The Random Deposition is the simplest growth model and it is very useful since one can write equations and calculate exactly the scaling exponents.

The crossover time (also called saturation time) depends on the linear size L of the system, in the form t_x ~L^z, where z is the third critical scaling exponent, called “dynamic exponent“. The scaling exponents α, β, and z are interconnected via the relation³ [FAM85]:

(5)

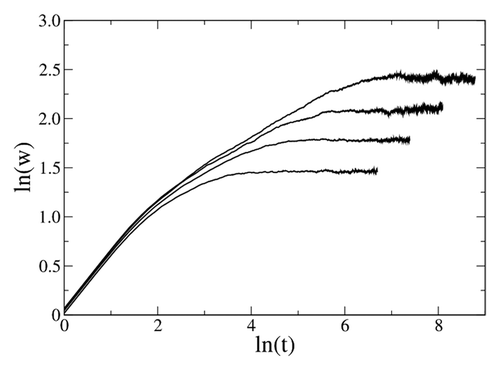
In some growth models it is possible to observe two (or more) different behaviors of the roughness for the growth regime, before the system reaches the saturation regime.⁴,⁵ In these cases, one or more exponents β can be found for t << t_x, as can be seen in Figure 1.

Figure 1. Temporal evolution of the roughness for different network sizes.⁴,⁵

Diffusion parameters

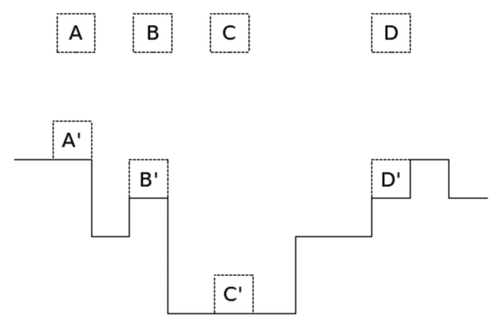
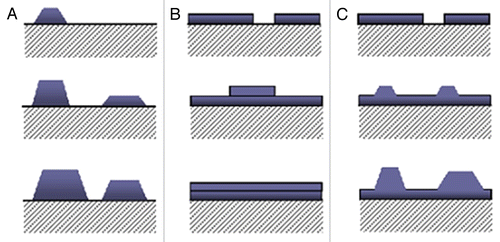
The “search” for the most convenient position (lowest height position or the energetically most favorable) on the surface occurs through the atom/molecule diffusion. The evolution of the surface roughness during the deposition of a thin film depends strongly on the possibility of diffusion of atoms deposited on the surface. Diffusion plays an important role in the surface roughness: by introducing correlations among neighboring sites, the surface roughness becomes smooth and eventually saturates. The “diffusion length,” i.e., the distance that an atom/molecule can move until reaching the final position, can be very large and depends on some factors during deposition, such as temperature and energy barriers. The growth can occur in the form of islands (Volts-Amperes) of layers (Frank-Van der Merwe), or in an intermediate form island-layer (Stranski-Krastanov). These processes are represented in Figure 2, at different times of coverage of the substrate.

Figure 2. Different modes of thin film growth. (A) Growth in islands, (B) Growth in mono-layers and (C) mix growth of islands-layers.

The growth form is determined by the energy of atom-surface interactions. The variation of surface energy is defined:

(6)

∆γ = γ_S − γ_A − γ_I,

where γ_S is the surface energy of the substrate, γ_A the energy of the adsorbed layer and γ_I is the tension of the interface. In the case of Δγ > 0 the growth occurs as layer by layer, since the surface energy of the substrate favors the planar deposition and the next layer will grow only after complete coverage of the substrate. For the case of Δγ < 0, the tension of the interface increased, favoring the growth of the deposited material forming islands on the substrate. An intermediate situation can occur when, in the beginning of the process, Δγ > 0 condition favors the growth of layers up to a critical thickness, and then starts to form islands of material deposited on the substrate (model described by Stranski and Krastanov).

Models of Surface Growth

The models defined as “discrete” can be directly studied by numerical calculations and computer simulations. These models simplify the real conditions of growth and each one reflects a specific growth condition. The principal discrete models are the Random, the Ballistic, and the Solid on Solid (SOS).

Random deposition

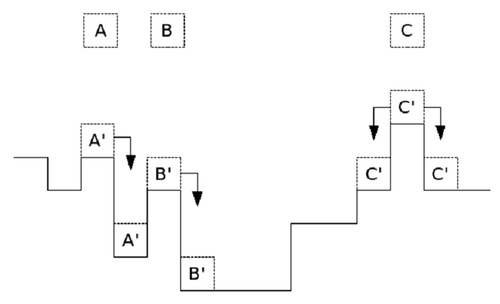
This is the simplest model, with exact solution. In this model the roughness does not show saturation and grows indefinitely over time. The construction rule for this model is that each particle is deposited in a random place of a network of size L, occupying the position immediately above the surface at the site, as shown in Figure 3.

Figure 3. Rule deposition in the random model.

In this model the interface has no formation of pores in the volume. A way to represent the temporal evolution of the interface is to associate a stochastic equation to it. The variation of height h(x,t) can represent statistical characteristics of the interface:

(7)

Φ(x,t) is the number of particles per unit time that is aggregated at position x and time t. The term Φ(x,t), due to random feature can be represented as a sum of two terms, and Equation 7 becomes:

(8)

F is the average number of particles per unit time added to the substrate at position x and η(x,t) represents a “noise,” the random fluctuation of this process, without spatial correlation on the substrate:

(9)

The second moment of this noise is:

(10)

in order to indicate no correlation between space and time. Integrating Equation 8 in time:

(11)

The average height of the interface becomes:

(12)

< h(x,t) > = Ft

Squaring Equation 11:

(13)

< h²(x,t) > = F²t² + Ct

The interface width is so w²(t) = Ct, and so:

(14)

From Equation 3(3) , β = 1/2.

This model presented the condition of no roughness growth saturation. Generally, this is not the real condition of growth of a film, and needs to be improved; generally, the atoms/particles forming a film have a certain freedom of movement on the surface, so random models with surface relaxation present more appropriate conditions to describing the particles deposition with superficial diffusion.

Random deposition model with surface relaxation: Edwards-Wilkinson equation

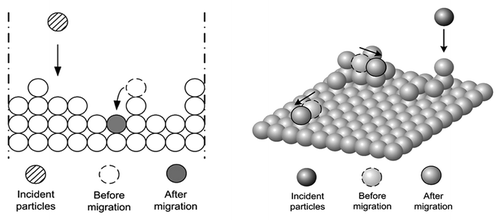
To approximate the random model to a real condition, a term is added to include the mobility of atoms or particles arriving on a surface; this term represents the spatial correlation between the sites where the particles deposit and the first neighboring sites. This correlation determines the saturation to a maximum value of the roughness. Once deposited, the particle “demand,” among neighboring sites, that one of smaller height, as shown in Figure 4.

Figure 4. Dynamic of random deposition of the particles, with surface relaxation.

If these sites have the same height, the particle is randomly placed, or in the initial site or in one of its first neighbors. The model has no exact solution, contrary to what happens in the random model, but it is possible to associate with the model a stochastic differential equation. From this equation and using symmetry arguments, it is possible to define the exponents of this model of growth. Also this model, as the random deposition model, does not show porosity in the deposited film.

The differential equation which represents the condition of deposition is:

(14)

and G(h,x,t) in this case also depends on the height h due to the fact that the film has a roughness maximum height then depends upon the surface; the dependence on x position is due to the spatial correlation between the site of deposition and neighboring sites. The symmetry arguments considered¹ define the deposition conditions such as:

(1) Temporal invariance: T → t + dt

This requirement states that G = G(h, x).

(2) Translational invariance (growth direction): h → h + δh.

To satisfy this invariance, it is necessary that G = G(∇hn,x), …. Δhⁿ since h is invariant against this translation.

(3) Translational invariance (in the direction orthogonal to growth): x → x + δx. In this case G = G(∇hⁿ).

(4) Inversion’s and rotation’s symmetry around the direction of growth: to satisfy this condition, is not allowed the presence of the derivatives terms of odd order, so that G = G(∇^2Kh), or G = G(∇ ^2K+1h) ^2l.

(5) Symmetry up/down, h → - h.

With these conditions of symmetry, the equation that describes the model becomes a stochastic form equation:

(15)

The higher orders terms can be unconsidered, provided the hydrodynamic properties of scale growth surface. The equation then becomes:

(15)

This is the Edwards - Wilkinson equation.⁶ The term ν∇ ²h is the surface tension and the term is the noise (“white noise”). From this equation can be determined the stochastic growth exponents; calculating the Fourier transform of Equation 15 is obtained the correlation function between the points of the surface, and finally the inverse transform is calculated, obtaining the values of the exponents growth:⁶,³

(16)

α = (2-d)/2; β = (2 – d)/4; z = 2 [EW].

Model of ballistic deposition

The ballistic deposition is the simplest model that presents porosity. This model also includes correlation between more distant neighbors; the particles are deposited randomly on the surface and are correlated with any site that presents the first contact with the interface. That condition enables the formation of voids, or porosity, inducing a porous structure in the film during its formation because the interface can also grow tangentially to the surface of the initial substrate. The roughness evolves, after an initial time t_x, to saturation, and in this model the growth exponents are α ≈0:50 and β ≈0:33 for the one-dimensional condition, d = 1. The parameter d represents the dimension of the surface. The stochastic differential equation which represents the growth of the film for the BM is the equation developed by Kardar, Parisi, and Zhang, discussed in the next paragraph.

Equation Kardar-Parisi-Zhang (KPZ)

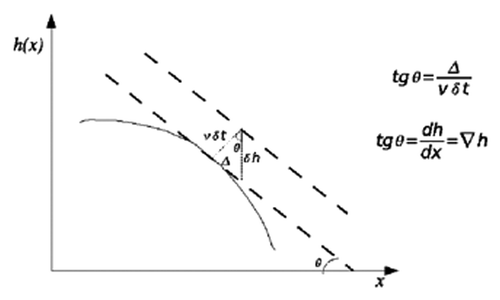
Kardar, Parisi, and Zhang proposed an analytical treatment to study the vapor phase deposition of thin films,⁹ adding to the EW equation a not linear term; this approach has been used in other models of deposition and formation of a thin films. The KPZ equation is obtained by using symmetry conditions, thus determining the exact values ​​of scaling exponents α and β. To build the KPZ equation it is maintained a characteristic obtained in the ballistic deposition model, i.e., the lateral growth of film due to aggregation of the particles arriving to the substrate in their first contact. This is represented in Figure 5; the term δh is along the growth direction and the term υδt normal to the interface.

Figure 5. Origin of the nonlinear term in the KPZ equation.

And then:

(17)

where Δ = υ tgδt. Since ∣∇ h ∣ < < 1, is possible to expand only up to second order:

(18)

The nonlinear term (∇ h)² represents the lateral growth of interface.

Adding this term to equation EW, we have:

(19)

known as KPZ equation; the first term describes the relaxation at the interface due to surface tension v and the last term represents the noise, without correlations in space and time.

This equation shows some properties of symmetry, but this symmetry is broken due to existence of a driving force F causing a film growth perpendicularly to the interface, generating a lateral component to direction of growing film. To determine the growth exponent associated to the KPZ equation is utilized the renormalization group theory, which represents an extremely useful tool in a large number of applications. For one-dimensional systems, the scaling exponents associated with the KPZ equation can be determined exactly. In this case, we have:

(19

The renormalization group provides exact solution for the scaling exponents only for the one-dimensional system. For higher dimensions, numerical simulations of this nonlinear model have provided increasingly accurate values ​​for the scaling exponents, depending on the improvement in computational processing.

There are a number of phenomena described in terms of a nonlinear theory, as which that describes the ballistic deposition. As example, models that can generate porosity have been extensively studied, with small variations from the standard ballistic deposition model and with improving accordance to real systems, being interesting in technological applications.

Model solid-on-solid (SOS)

This model provides some limiting conditions in previous models, necessary when some measures (h[i,t, ...]) have excessively large values. Such corrections were so applied in SOS models, where some boundary conditions allow minimizing the need for corrections of scale. In models SOS, for example, is considered a single line interfacing, which limits the difference in height between neighboring sites. The best known model is called RSOS (restricted solid-on-solid),¹ where the height of growth between neighboring sites is incremented by only one unit, so that |∆h| = 0,1.

Applications of the Models

Control of thickness, surface, roughness, and porosity of the growing films

In recent years is improving the interest on thin film’s models that could correlate its thickness, roughness, and porosity. The correlation between different factors depends, for example, on temperature and on the rate of deposition of atoms forming a film and these parameters influence directly the surface diffusion.⁷ In reference 8 is shown a procedure to better control these parameters by controlling the deposition rate.

The simulation method of Kinetic Monte Carlo (KMC) is effective to simulate the deposition of a thin film in these conditions. First the method is generally based on the approximations obtained by the SOS, which provides approximate description of the evolution of a film’s microstructure, providing feedback to implement the equation that describe the evolution of the surface roughness of the deposited film. This model includes the processes of adsorption and migration of atoms on the surface, which defines the surface roughness during the film formation (Fig. 6).

Figure 6. (A) Deposition process in growing a film in two-dimensional triangular lattice. The measure A is the diameter of particles, so La represents the lateral extent of the network. (B) Layout of adsorption and relaxation of the incident particle (A); (B) is the first particle observed by A on the surface, (C) is the nearest vacancy and (D) is the site where the atom A relaxes.¹⁰

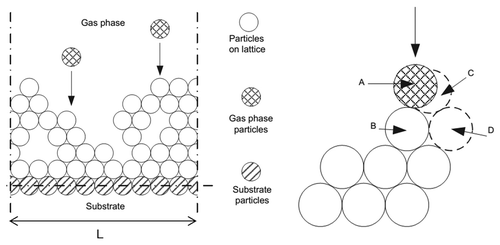
The migration process follows a behavior described by an Arrhenius equation:¹⁰

(7)

where ν₀ represents the pre-exponent factor, n_i is the number of the nearest neighbors of the ith particle and can take the values of two to five (r_m,i is zero when n_i = 6 since this particle is fully surrounded by other particles and cannot migrate), E₀ is the contribution to the activation energy barrier from each nearest neighbor, k_B is Boltzmann's constant and T is the substrate temperature of the thin film.

The representation of the porosity of the film is given by the ratio of sites occupation (SOR):

N is the total number of particles deposited in the crystal lattice, L is the number of deposition sites of the network and H represents the number of the deposited layers.

Using an Edwards–Wilkinson type equation, is defined the dynamic model of surface’s height h(t) and of SOR of the film, to preset roughness by manipulating the deposition rate (Fig. 7).

Figure 7. (A) Quadratic roughness (solid line) and film thickness (dashed - dotted line); roughness control for the minimum desired film thickness. (B) Simultaneous adjustment in thickness, surface roughness and porosity.¹⁰

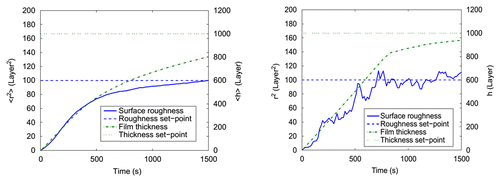
This simulation shows that the need for minimum film thickness with limited roughness would require a limitation in deposition rate, affecting the possible values ​​of porosity in the film.

A subsequent study conducted to describe the interdependence between surface roughness, slope of the surface in the process of migration of particles during deposition and size of the surface network was performed¹¹ in order to improve the control of the deposition parameters for simulating the growth of thin films on surfaces of silicon solar cells. The application of mathematical models in this case is essential for contributing to increase the efficiency of solar energy conversion. The average surface roughness and slope influence the rate of absorption by the semiconductor surface layers, of the light incident on the surface. The two types of models more used are the KMC model and the models of stochastic differential equations (SDE); KMC is based on predefined rules on a microscopic scale, while the SDE models also use experimental data of processing; however only SDE models provide a description which enables the feedback of experimental results, allowing the controlling of the surface roughness, porosity, and thickness of thin films.

The basis for defining the simulation models is the dynamics of the atoms / particles deposition on the surface, described trough two main models, the model RDSR (Random Deposition with Surface Relaxation) and the model that reproduces the migration of the particles surface; these dynamics are shown in Figure 8. The base of the models is the behavior SOS. These models contribute to controlling the deposited film for large-scale surface.

Figure 8. Model of deposition, relaxation and immediate migration of the particles (A) 1D model, (B) 2D Model.¹¹

The simultaneous control of surface roughness and mean slope of the surface is critical to optimize the surface reflectance and transmittance,¹² which is a key factor to improve the efficiency of photovoltaic solar cells; in fact, the scattering of light at the surface is directly correlated with absorption of light by the surface of the cells (Fig. 9).

Figure 9. Typical configuration of the solar cell composed of thin films with pin structure, the surface layer of TCO.

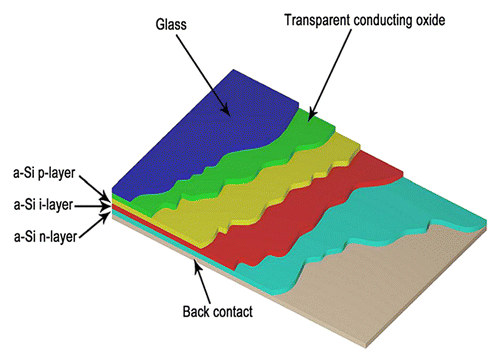
The dynamic of evolution of the surface can be described by an equation of Edward–Wilkinson type, which is a stochastic equation depicting the evolution of a surface growing as a function of the experimental parameters. This study is performed performing a controlled deposition rate by varying the surface temperature as a control parameter. The model allowed the simultaneous control of roughness, average slope of the surface, and consequently the possibility of depositing the film with the default values ​​of these parameters to optimize the reflectance and transmittance of the surface of the solar cell.

Another important application of thin film growth models is to control the deposition and to better define the structural properties of a DLC film.¹³ In this case the optimal control parameter is the energy of the incident particle to substrate. This determines the density of the film, the residual compressive strain and the fraction of sp₃ bonds determining the fraction of ratio diamond /graphite in the film, that define the properties of the film of DLC such as hardness, low friction coefficient, superior optical properties, and good inertia chemistry. The residual strength is a problem because it reduces the adhesion of the film, essential in many tribological applications. With the simulation it is possible to control the microstructure of the DLC, improving the adhesion of the film on the substrate, among other factors (Fig. 10).

Figure 10. Evolution of the microstructure of the DLC film as a function of energy deposition.¹³

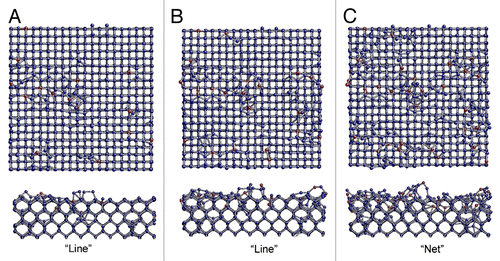
The mobility of the surface atoms incident shows dependence on the energy of deposition; the atoms undergo adsorption, reflection by the surface, or implantation depending on this energy. This determines the fraction of sp₃ bonds, influencing the DLC film quality; adsorption and reflection of atoms is detrimental to the quality of the film, reducing the fraction of sp₃ binding. Mathematical modeling of this type of surface growing can help to define the parameters during the formation of DLC film improving the performance in tribological applications and eventually helping to control the porosity of the DLC film. Figure 10 shows the simulation with the formation of peer- Line (point- line -net) of carbon atoms, implanted in the superficial network. The implantation of the atoms defines the rearrangement of the crystal structure, characterizing the DLC film quality (Fig. 11).¹³

Figure 11. Variation in the initial growth of the film with the incident energy of 70 eV/atom. The blue dots represent atoms of the substrate, the red dots deposited atoms.¹³

A carbon film, as the DLC or the ta-C (tetrahedral amorphous carbon), the toughest among the amorphous DLC, can form in conditions not direct dependent from high temperature and pressure, indicating the existence of other conditions that enable the formation of diamond, DLC or ta-C. There are already quantum models of electronic activation that determines the rearrangement of atoms, which leads to the formation of these materials without the need for high temperature and pressure, which was confirmed by Raman characterization.¹⁴

The study of the crystalline structure of these materials by means of quantum models may be accompanied by mathematical modeling, which could set the growth’s parameters compatible with the specific conditions of carbonaceous materials films. The construction of computational models will facilitate the control of the growth of DLC or ta-C with closed models created from the processing conditions (P, T, atmosphere etc).

Applications to biomaterials

The understanding of stochastic process related to surface growth creates the possibility of developing thin film devices with desired properties for technological and medical applications, such as the stent devices. Besides the applications in control of thickness, surface roughness and porosity of the films, the control of the coating process and of the adherence of electrodeposited films used in stent devices is crucial to keep the mechanical properties.

One can focus the attention on two main issues in these devices: (1) the deterioration of the material caused by ruptures generated due fatigue-crack growth and corrosion phenomena, and (2) the biomaterial encrustation on the devices. The fatigue due to tens of millions of loading cycles may result in fracture or even failures of the stents. For many materials, fatigue-crack growth and fracture toughness is well documented¹⁵ and still unknown. In other stent applications, such as ureteral stents, the long-term use of the material may lead the device to the problem of biomaterial (microbial biofilm) encrustation.

Despite the large amount of experimental studies related to in vivo and in vitro stent devices, only few theoretical studies have been proposed and none have focused on the theoretical analysis of the surface properties of these materials.¹⁶ The surface roughness for different coating surfaces of materials used in stent devices have been experimentally analyzed in some studies.¹⁷ However, theoretical approaches and computational techniques to simulate and analyze materials, extensively used in physics and materials science, have not been applied. Due to the reduced costs and potential applications in the development of new materials, thin films simulations can be extensively employed in biomaterials analysis.

In the case of fatigue-crack growth and fractures, the use of computational growth models can mimic the fracture in the material and provide information about long-term integrity of the stents. Some experiments on ruptures describe the fractured material in terms of self-similar concepts and this rupture can be understood in terms of directed polymers in random media. Directed polymers in random media are usually mapped by the KPZ equation, which provides theoretical understanding of the surface.¹

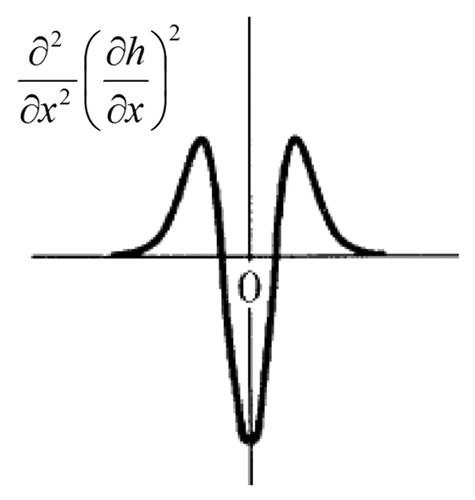
A nonlinear differential equation, distinct from the KPZ equation, takes into account nonlinear effects due to the chemical potential, such as surface diffusion. This equation was originally proposed by Lai and Das Sarma¹⁸ motivated by MBE process at high temperature; in this condition the surface diffusion plays an important role in the growing process. This equation,

(8)

takes into account the surface diffusion and may represent a simplified model for an ideal MBE growth, as pointed out by Lai and Das Sarma. The nonlinear term can be interpreted, geometrically, as a segment of the surface as one can see in Figure 12, this equation⁸ exhibits a conserved dynamic and non-conservative noise and it is usually represented by symbol NCN4 (nonlinear conservative dynamics, non-conservatives noise).¹ By the Renormalization Group analysis, this equation can be exactly solved and, for a fractal dimension d = 2, the exponents are α = 2/3, β = 1/5 and z = 10/3. One can even consider an extension of the KPZ Equation 8 that is a most general equation, namely,

Figure 12. Segment of the surface, adapted from reference 18.

(9)

Equation 9 takes into account relaxation mechanisms, lateral growth, surface diffusion, and desorption. A mathematical model described by this equation can be the starting point for the study of ultrathin films coatings with complex characteristics, such as porosity and pinholes, resulting from the process of film growth.¹⁹ Regarding to medical applications of surface coatings, as stent coatings¹⁹ we believe that this equation can mimic the process and, in principle, be useful to the study and improvement of this class of surface growth. Since this equation have exact exponents only for the one-dimensional case, further numerical analysis and simulations are needed to describe accurately these processes.

The encrustation of biomaterials on the stent, mostly related to the ureteral use but also occurring due to formation of thin films due to platelet adhesion, is the most directly application of the theoretical surface analysis. Image analysis using SEM and AFM provides high quality topological informations of the surface roughness on several different coating materials. By the knowledge of the surface exponents, as seen in the second chapter of this paper, it’s possible to characterize the theoretical model of surface growth, at least the closest one to the specific problem. Once the surface is classified into a known model and belongs to a universality class of problems, one can run simulations and predict many properties of the surface and, consequently, of the stent device.

Conclusions and Future Developments

This paper is a quick review of simulation results for parameter control of thin film deposition. The requirement to control the properties of the deposited films, such as roughness, porosity and thickness of the film, indicate the great importance to control the growth surface process. The use of computer simulation models is a method increasingly useful for controlled processes, requiring further development to direct methods and processes for thin film deposition.

The second part of this work will be developed in the application of theoretical models to control the growth and adherence of electrodeposited films used in stent devices; the models will be helpful to resolve the problem of superficial defects evidenced in the characterization of stents.¹⁹

At the same time, the models will be applied in study of deposition of magnetic films, DLC films with optical and tribological properties and to control the properties of TOC films used in solar cells. The models will be used also to better control of nano-structured films as graphene layer.

Abbreviations:
t	=	time
x	=	position of the column
h(x,t)	=	height of column x at time t
L	=	linear size of the substrate
w(L,t)	=	interface width
Φ(x,t)	=	function of the number of particles at position x at time t
z	=	dynamic exponent
MBE	=	molecular beam epitaxy
SOS	=	solid on solid
EW	=	Edwards-Wilkinson
KPZ	=	Kardar-Parisi-Zhang
KMC	=	kinetic Monte Carlo
SDE	=	stochastic differential equations
TCO	=	transparent conducting oxide
DLC	=	diamond-like carbon
RDSR	=	random deposition with surface relaxation
α	=	roughness exponent
β	=	growth exponent
ρ	=	porosity
η	=	noise
max	=	maximum
sat	=	saturation
x	=	crossover

Disclosure of Potential Conflicts of Interest

No potential conflicts of interest were disclosed.

10.4161/biom.28871