An Elasto-Plastic Model of Avian Gastrulation

Abstract

The motions observed during avian gastrulation may be simply interpreted in terms of elasto-plastic flow of sheets. Such a model allows one to calculate the flow map inside the blastodisc, hence the evolution of its shape. In addition, the model predicts that there exists a region of high stress oriented radially from the caudal pole towards the center of the blastodisc, with a tensile component oriented orthoradially. If the stress generated by cellular motion is enough to provoke a crack in the extra cellular matrix, then mesoderm ingression proceeds through a "streak" (the primitive streak) oriented from the caudal pole inwards, which relieves the stress while it creates the 3 germ layers. The model predicts that crack opening is next followed by crack retreat (primitive streak retreat), as mesoderm ingression continues. As mesoderm ingression proceeds around the area pellucida, similar phenomena in the anterior pole may contribute to formation of the embryo. This gives a mechanical description of avian gastrulation which complements the biochemical approach. In addition, the model provides a simple explanation to the shape of the embryo at very early stages, and possibly an explanation of the entry point of the vitteline arteries into the mesoderm.

Introduction: A Simple Description of Avian Gastrulation

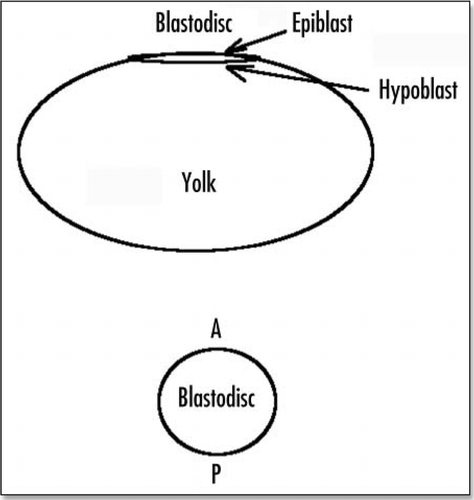
Gastrulation proceeds along diffferent ways in different organisms. In avian development, the embryo passes through ovocyte, morula and blastula stages, and then forms a blastodisc, which is a flat disc, two layers thick, partially delaminated, resting on a cavity (the blastocoel) itself resting on the top of the yolk of the egg (Fig. 1). At the stage where the egg is laid, the blastodisc contains about 20,000 cells. The presence of the huge amount of yolk (megalolecithal egg1) is probably the cause, or at least an indirect cause of the formation of a flat blastula, as compared to the round blastula of eggs which lack yolk (esp. mammals). The cell layers composing the blastoderm are delaminated over one half (the caudal half).

Early after being laid, the avian egg will undergo gastrulation. This gastrulation is well documented. It requires a huge cellular motion which has the shape of two vortices converging towards the posterior pole an along the antero-posterior (AP) axis (Fig. 2), where a groove forms (the “primitive streak”). Numerous movies of such a motion are available on line at different web sites, such as www.gastrulation.org. Along this primitive streak, cells from the top layer of the blastoderm will ingress and “flow” underneath, to form several tissues, especially, the extra-embryonic organs, such as the mesoderm of the yolk-sac. The primitive streak posesses a special region at its apex, known as Hensen's node, which has organizing properties for the embryo growth.1 At the posterior pole, prior to gastrulation, the blastodisc has a special region, Kohler's sickle, which is thought to be the organizer of the AP anisotropy (Fig. 1).

In this article, I shall present a physical model of avian gastrulation, from the blastodisc stage up to mesoderm ingression and almost to the point where the vitteline arteries are formed. The paper is organized as follows: in the first part, I present the physical description of deformations inside the blastodisc, considered as a flat circular “pancake”, as can be deduced from linear elasticity analysis. The main result of this part is that the deformations inside such a flat disk have a Poiseuille (parabolic) profile. People who are not familiar with elasticity should go directly to the Equs. 7Equ. 7 $\text{U(x,y,z)}=\text{U(x,y).(h/2-z) (h/2+z)}{\text{.4/h}}^{\text{2}}$Equ. 7 –8Equ. 8 $\text{U(x,y)}={\text{ -(h}}^{\text{2}}\text{/E8)gradP}$Equ. 8 and (Fig. 3), which give the deformation in the cross-section of the blastodisc. Following the description of deformation in the blastodisc, I describe Kohler's sickle, and how it comes into play as a force term in the deformation equation. Adding this force term to the problem, I am able to find the “flow” inside the blastodisc (analytically), by classical fluid mechanics techniques (namely, stream function, and delta force distribution analysis). I give the shape of the vortex in the mesoderm. I provide a general expression in which as many force terms as observed can be added. People who are not familiar with hydrodynamics should go directly to Equ. 16Equ. 16 $\psi =\left(3{\text{fh}}^{\text{2}}/4\text{E}\right)\left(\text{y/}\left[{\left(\text{x}-\text{a}\right)}^2+{\text{y}}^{\text{2}}\right]-\text{y/}\left[{\left(\text{x}-\text{a}\right)}^2+{\text{y}}^{\text{2}}\right]\right)$Equ. 16 and Figures 5 and 6, which give the “flow” profile in the blastodisc, as seen from top. Following the calculation of the “flow” map, I find the evolution of the blastodisc during the early moments of gastrulation, and show how it corresponds to what is observed (Fig. 7A and B, and Fig. 8A and B). I next introduce a simple mechanical criterium for rupture of the extra cellular matrix, and explain why and how a crack should form in the blastodisc, allowing ingression of the mesoderm through a “primitive streak”. The origin of this crack is in the distribution of stress along the axis of the blastodisc, during the vortex motion: this stress has one main component oriented orthoradially, all along a line starting from Kohler's sickle and going away from it in both the A and P direction (Fig. 10). People who are not familiar with physics of rupture should go directly to Figure 9 which gives the stress map, and especially the zone of high tension which is most likely to break. I then describe qualitatively the evolution of the mesoderm inside the primitive streak, an explain why primitive streak retreat should be observed. Finally, I show that the contraction of the blastodisc creates naturally a path for the vitelline arteries, at right angles to the body axis. I then conclude that the incorporation of mechanical forces in this problem is unavoidable, and that models of avian gastrulation limited to genetical facts are inappropriate. Finally, I speculate that this mechanism is more general than avian gastrulation.

Physical Description of Deformations Inside the Blastodisc

The most obvious feature of gastrulation is the vortex motion of the cells which converge towards the (presumptive) caudal pole. It has long been known that if this “flow” of cells is impeded, primitive streak will not form.2 Also, it has long been known that mechanical forces exerted by cells play a crucial role in gastrulation events.1 Therefore, there is little doubt that the primitive streak formation, and the concomitant blastodisc deformation are consubstantial of the cellular “flow” towards the posterior pole. In this view, the principal morphogene of blastodisc deformation and of primitive streak formation should be a mechanical parameter, such as the flow map V(x,y,z) in the blastodisc, and related quantities, such as the stress field σ_ijk(x,y,z), but are these defined, since living tissue is not a liquid? The first step, in order to understand the process of gastrulation is to reach a physical description of such a vortex motion of the blastodisc layers (epiblast and hypoblast).

From a fundamental point of view (Newton's law) stresses relate to speeds for liquids, and stresses relate to deformations for solids. The fluid speed is technically a “deformation rate”. In the case of liquids, the ratio between deformation rate and stress is the viscosity : the more viscous, the more difficult the flow, for a given stress. In the case of solids, the static deformation is proportional to forces, and the ratio of the two is the elastic modulus (equivalent to a spring stiffness): the bigger the elastic modulus, the smaller the deformations, for a given stress.

The embryonic sheets are certainly not liquids, since they can be handled micro-surgically like solid foils (although very soft). Moreover, embryonic sheets bear the tension of the yolk membrane. However, their motion and growth is obviously associated to deformation rates, as appears on the accelerated time-lapse movies. This implies that the deformation of the sheets is plastic, i.e., above certain thresholds, the deformation is “for good”. There exist several types of plastic deformation. In the simplest case, above a certain stress threshold (or a combination of stress components) the solid is plastically deformed (yield). In mechanics, such yield thresholds are known as yield criteria, two well known criteria are Beltrami's or von Mises' criteria. The latter, for example, states that the solid yields if the following combination of stress : σ₁² + σ₂² + σ₃² - (σ₁σ₂ + σ₁σ₃ + σ₃σ₂) exceeds a given material value σ_m, where σ_i's are principal stresses. (A typical value is of 1 kg for 10 cm × 10 cm for a thin plastic bag, this is why one avoids putting all heavy items in the same bag when returning from a store).

In this view, the progressive “flow” of the embryonic sheets can be viewed as a step-by-step deformation and yield of a very soft solid. The sheet is not truly viscous, its instantaneous viscosity is not a quantity which is defined (as for a liquid), and, under a stretch or compressive force, there is only an instantaneous deformation, which may, or may not be definitive. Therefore, the first step in modelling the vortex motion is to calculate the elastic deformation of the blastodisc sheets.

We now apply the physics of elastic deformation of a thin solid sheet to the blastodisc situation. We assume that the blastodisc is a composite structure, namely a “sandwich”: Extra-Cellular Matrix/cellular layers/Extra-Cellular Matrix. This composite structure is created by apicobasal asymmetry of cells inherited from dorso-ventral anisotropy of the ovocyte. The ECM is supposed to be a strong collagenous membrane which bears most of the mechanical load. Also, as being essentially a polymer sheet, it is supposed to be less plastic than cells themselves (i.e., since ECM is fabricated by cells, ECM adaptation to forces is slower than cellular adaptation to forces). In order to relate deformation to forces in this sandwich, we write first the stress tensor σ_ij for an incompressible solid; this stress tensor is related to the strain ε_ij by:5,6 Equ. 1 ${\sigma }_{\text{ij}}=-\text{P}{\delta }_{\text{ij}}+(2\text{E/3}){\epsilon }_{\text{ij}},$Equ. 1

The stress tensor is the operator which relates small deformations to small forces per unit area (stresses). The simplest of all stresses is pressure (pressure stress = the pressure), which is a force per unit area. In addition, there can be, in a solid, other forces. For example, a small increment of deformation, say along the x direction (Fig. 3), is associated to a uniaxial force in the × direction, and also to smaller forces in the perpendicular directions (think of a rubber eraser: if compressed vertically on a table, there is also a force and a deformation parallel to the table, but smaller than the vertical compression). Please refer to a general elasticity textbook for a detailed description of this formalism.

The strain tensor is, as usual, related to the displacement vector u_i by Equ. 2 ${\epsilon }_{\text{ij}}=1/2({\text{du}}_{\text{i}}/{\text{dx}}_{\text{j}}+{\text{du}}_{\text{j}}/{\text{dx}}_{\text{i}})$Equ. 2

Please remember that it is not displacements which create forces, but variations in displacements. A global uniform displacement does not create any force. The derivatives of displacements correspond to the solid deformations (strain tensor), which are related to the stresses. As for a spring, elastic forces are related to differences in displacements between two ends of a small volume, and not to absolute displacements (idem a compressed spring exerts a force, a uniformly displaced spring does not).

Since we describe the epiblast as a very thin soft layer crawling between two stronger membranes (the associated ECM), we find for the deformation, a situation which is analogous to a Poiseuille flow between plates (Fig. 3), except that instead of a Poiseuille flow between plates, we have a “Poiseuille deformation” between two stiffer extra cellular membranes (ECM). In the case of a Poiseuille flow, the equilibrium condition defines the deformation rate, while in the case of a thin elastic solid layer embedded between two foils of ECM, the equilibrium condition fixes the deformation itself (no flow) (Fig. 3). In the first case, the force serves the sliding of fluid lamina which dissipates the energy, while in the second case, the deformation of the lamina stores the elastic energy. (Here, the infinitesimal lamina of thickness dz is a mathematical infinitely small layer, needed for a mathematical integration, it is not a tissue layer). Whatsoever, for a laminar approximation in the epiblast, the deformation perpendicular to the lamina is zero. Let us consider the problem in the cross section of the blastodisc we get: ${\epsilon }_{\text{xx}}={\text{du}}_{\text{x}}/\text{dx\hspace{0.17em}}{\epsilon }_{\text{xz}}=1/2{\text{du}}_{\text{x}}/\text{dz\hspace{0.17em}}{\epsilon }_{\text{zz}}=0$

This simply means that each lamina is essentially sheared by du_x/dz in the longitudinal x direction, and stretched by du_x/dx. The equilibrium condition δ_iσ_ij = 0 then gives along x: Equ. 3 ${\text{-d}}_{\text{x}}\text{P}+(2\text{E/3}){\text{d}}^{\text{2}}{\text{u}}_{\text{x}}/\text{dx2}+{\text{d}}_{\text{z}}\text{P}+(\text{E/3}){\text{d}}^{\text{2}}{\text{u}}_{\text{x}}/{\text{dz}}^{\text{2}}=0$Equ. 3 with u_x = 0 on the top and bottom ECM. If we neglect the variation of P in the z direction, because the blastodisc is very thin (typically 30 µm), we get: Equ. 4 ${\text{d}}_{\text{x}}\text{P}+(2\text{E/3}){\text{d}}^{\text{2}}{\text{u}}_{\text{x}}/{\text{dx}}^{\text{2}}+(\text{E/3}){\text{d}}^{\text{2}}{\text{u}}_{\text{x}}/{\text{dz}}^{\text{2}}=0$Equ. 4

This is a classical differential equation, analogous to the Poiseuille equation for liquids, although we deal here with deformations. This equation reduces to Equ. 5 ${\text{d}}_{\text{x}}\text{P}+(\text{E/3}){\text{d}}^{\text{2}}{\text{u}}_{\text{x}}/{\text{dz}}^{\text{2}}=0$Equ. 5 considering that the contribution of shear force across the thin layer of thickness h is much bigger than the stretch in the tangent direction (“lubrication” approximation). h is of the order of one, or just a few cell thicknesses. The origin of this simplification of the equation is in the magnitude of the derivatives of the displacements: if a material is extremely thin, and attached to a substrate (and we think here of cell layers as being like that), then any force exerted on it provokes a shear much bigger than a compression. This is because the displacement varies between 0 and u_max over a very small distance (h), hence the shear is of order u_max/h while the displacement in the tangent plane varies as u_max/(blastodisc diameter), which is obviously smaller, since the blastodisc diameter is orders of magnitude larger than its thickness (as stated before, the number of cells is of the order 20,000 when the egg is laid, hence of the order of 50,000 at gastrulation, therefore, the diameter is of the order of 100 times the thickness).

Here, a remark imposes itself : it is this very fact (ratio diameter/thickness ∼100) that makes the gastrulation of avian blastodiscs amenable to an analytical description. In the case of mammals, the blastula is a spheroid, and all deformation terms, in 3D, must be kept in Equations 1Equ. 1 ${\sigma }_{\text{ij}}=-\text{P}{\delta }_{\text{ij}}+(2\text{E/3}){\epsilon }_{\text{ij}},$Equ. 1 and 2Equ. 2 ${\epsilon }_{\text{ij}}=1/2({\text{du}}_{\text{i}}/{\text{dx}}_{\text{j}}+{\text{du}}_{\text{j}}/{\text{dx}}_{\text{i}})$Equ. 2 above, which renders the problem extremely difficult. To our knowledge, there does not exist any analytical model of blastopore formation, and blastula invagination, although the role of mechanical forces has for long been invoked.

Returning to our problem, the solution of Equation 4Equ. 4 ${\text{d}}_{\text{x}}\text{P}+(2\text{E/3}){\text{d}}^{\text{2}}{\text{u}}_{\text{x}}/{\text{dx}}^{\text{2}}+(\text{E/3}){\text{d}}^{\text{2}}{\text{u}}_{\text{x}}/{\text{dz}}^{\text{2}}=0$Equ. 4 is simply a parabolic variation of the deformation. Each (mathematical) lamina is basically translated sideways by a displacement u_x(z) depending on its position z in the epiblast layer, given by: Equ. 6 ${\text{u}}_{\text{x}}\left(\text{z}\right)=-(1\text{/2E})\left(\text{h/2-z}\right)\left(\text{h/2+z}\right){\text{grad}}_{\text{x}}\text{P}\left(\text{x}\right)$Equ. 6 where the origin is placed in the middle lamina. Locally, the gradient of pressure is opposed by the resistance to shear of the elastic solid, with a parabolic variation, from one lamina to the other, analogous to the Poiseuille fluid flow. Therefore, within the two assumptions:

1. The aspect ration of the blastodisc is great (the disc is flat)

2. The ECM is stiffer than the cells this result is exact.

For the 2D case in a thin flat sheet of thickness h, we assume a parabolic variation such that the displacement reads: Equ. 7 $\text{U(x,y,z)}=\text{U(x,y).(h/2-z) (h/2+z)}{\text{.4/h}}^{\text{2}}$Equ. 7

Where U(x,y) is the in-plane displacement of the middle lamina. U(x,y,z) is the complete 3D displacement field, but it reduces to the product of a parabolic profile, and a maximum displacement midway in the blastodisc U(x,y). Although the formalism may seem finally 2D, it grasps fully the 3D aspects. Keeping only the strongly varying terms of the stress equilibrium equation (the shear along x and y of laminae stratified in z) one gets: Equ. 8 $\text{U(x,y)}={\text{ -(h}}^{\text{2}}\text{/E8)gradP}$Equ. 8

This result states that the deformation is proportional to the gradient of pressure inside the cellular layer forming the blastodisc, a rather remarkable fact. Now, if we assume that the living material reacts plastically to the shear stress (yield), we see that the growth of the cell layers in between ECM amounts to a step-by-step elastoplastic “flow” governed by the gradient of pressure between the two ends of the solid compartment. In this picture, the impression given by the movies that the blastodisc seems to “flow” is not a consequence of its intrinsic material properties, but of the geometrical fact that the blastodisc is a thin layer. The speed V(x,y,z) mentionned above in introduction is not truly a fluid speed, it is proportional to the instantaneous deformation U(x,y,z) found above, with a prefactor which is the time constant of tissue adaptation. The ratio of stress over deformation rate is some sort of equivalent tissue “viscosity”, although the solid is not a fluid. We therefore always keep “flow” into brackets when talking of epiblast “flow”.

Kohler's Sickle as “Flow” Source

Our ambition, now, is to find the “flow” map in the blastodisc. We shall reach in the following paragraph an analytical description of this “flow”. In order to do so, we have to couple the Poiseuille elasto-plastic deformation, to the source terms for the “flow”. The equations found above relate readily the deformation, and the observed deformation rate, to the pressure force. In the case of an additional force term which drives the “flow”, the surface stresses are still: σ_ij = -Pδ_ij + (2E/3) ε_ij, but the equilibrium condition on a little element of volume now writes: ${\delta }_{\text{i}}{\sigma }_{\text{ij}}=-\text{f}$

The left hand side term corresponds to the bilan of all forces exerted on the surfaces of the little volume, and the right hand side corresponds to the volume force added to the problem, if any. When the derivatives of σ_ij are written analytically and added up, one finds an equation analogous to Stokes equation for slow fluid flow, and it writes: Equ. 9 $\text{-gradP}+({\text{h}}^{\text{2}}/24\text{E})\Delta \text{U}=-\text{f}$Equ. 9

A few technical steps must now be performed. In order to eliminate pressure, one takes the curl of this equation and deals with: Equ. 10 $({\text{h}}^{\text{2}}/24\text{E})\Delta \text{curlU}+\text{curlf}=0$Equ. 10

Now, we have seen above that the deformation is Poiseuille-like: $\text{U(x,y,z)}=\text{U(x,y).(h/2-z)(h/2+z)}{\text{.4/h}}^{\text{2}}$

In this case, the laplacian can be written: Equ. 11 $\Delta \text{U}={\text{U(x,y) d}}^{\text{2}}[\text{h}/2-\text{z) (h}/2+\text{z)}{\text{.4/h}}^{\text{2}}]/{\text{dz}}^{\text{2}}$Equ. 11

The other terms are negligible. (This again comes from the fact that curvature is much smaller in the plane than perpendicularly to the plane).

As a consequence, the flow U(x,y) in the plane of the blastodisc satisfies: Equ. 12 ${\text{(h}}^{\text{2}}/3\text{E)curlU(x,y)}=-\text{curlf}$Equ. 12

It is classical in 2D hydrodynamics to introduce the stream vector ψ such that

#x003C8; = (0,0, #x003C8;(x,y)), and #x003C8;(x,y) is the stream function, i.e., U(x,y) = curl#x003C8;, U(x,y) = (d_y#x003C8;, −d_x#x003C8;).

The lines of constant #x003C8; are the flow lines. A consequence of this formalism is that #x003C8; satisfies the simple scalar equation: Equ. 13 $\Delta \psi =(3{\text{E/h}}^{\text{2}})({\text{d}}_{\text{y}}{\text{ f}}_{\text{x}}-{\text{d}}_{\text{x}}{\text{ f}}_{\text{y}})$Equ. 13

Given the distribution of forces inside Kohler's sickle, the “flow” map is obtained again, exactly by solving this equation.

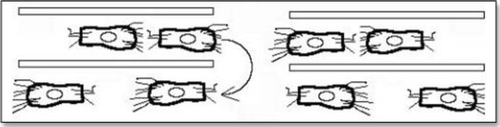
We now make an assumption about the force term. It is well established that the “flow” map is oriented towards the caudal pole, where this specific region (Kohler's sickle) provides an attractant center for cells. The origin of cell motility in the blastoderm is not clearly established, however, it has been shown that some cell types of the mesoderm crawl by a process of filopodia extension and retraction.7 This is especially true of endothelial cells, which have filopodia quite reminiscent of filopodia of the growth cone of neurons. Therefore, we may consider that cells exert a traction by extending filopodia on the ECM, and pulling themselves forward. There may be other motility mechanisms, especially, there may be anisotropies of membrane cell adhesion molecules, and cellular cytoskeleton traction. In this case, the mechanical traction force is entirely internal to the cell, as opposed to the filopodia case. The fact that cells exert tractions in this way, on the surrounding external medium is well documented. The traction itself induces a cascade of events by a general class of mechanisms called “mechanosensing”. These mechanisms may be of different sorts. Cells may be, as a whole, mechanosensors, since all chemical equilibria depend on pressure. In addition, there exist more specific molecular sensings, especially a number of adhesion molecules have been identified which link the cytoskeletton to the extracellular matrix, by means of transmembrane molecules (integrin receptors). The traction exerted by the cell will induce signalling, through adhesion-mediated cytoskeleton deformation. These phenomena have been reviewed recently.8 However, it makes no difference for the argument whether the cell motility is by filopodia traction or by transmembrane cytoskeleton contractility. If we represent the situation as in Figure 10, as seen from a cross-section of the blastoderm, and facing “six o'clock” at the posterior pole, we see that the cells present to the left exert a traction on the surroundings oriented towards the left, by which they move forward. If we consider that this behaviour is restricted to Kohler's sickle, we see that the presence of this region amounts to a distribution of forces on the moving cells, oriented towards the caudal pole (Fig. 4).

We therefore simplify the problem by considering that the force in Kohler's sickle amounts to one force to the left oriented towards the right plus one force to the right oriented towards the left. In mathematical terms we then write: Equ. 14 $\text{f = f}\left(\delta \left(\text{x}+\text{a}\right)-\delta \left(\text{x}-\text{a}\right)\right)\text{x}$Equ. 14 where δ is a Dirac delta function locating the force, x the unit vector along Kohler's sickle (ortho-radial vector at six o'clock).

The δ(x + a) term describes the localized force located at some distance a from the caudal pole, but to the left, and the other term the localized force at the caudal pole, but somewhat to the right. They are oriented in opposite directions, along the x axis (hence +x and −x), f is the magnitude.

The “flow” map for this force distribution satisfies: Equ. 15 $\Delta \psi =\left(3{\text{fh}}^{\text{2}}/\text{E}\right)\text{d}\left(\delta \left(\text{x}+\text{a}\right)-\delta \left(\text{x}-\text{a}\right)\right)/\text{dy}$Equ. 15

In order to treat a more complex force distribution, one could simply add up more force terms (linear additivity of the laplacian operator).

The extraordinary fact is that this equation is exactly the equation for two magnetic dipoles located at +a and −a near the caudal pole.8 The “magnetic field” in the plane of the blastodisc is the deformation map (or solid “flow” speed), the dipoles are the localized forces, oriented head-to-head. The solution to this equation is exactly known:9 Equ. 16 $\psi =\left(3{\text{fh}}^{\text{2}}/4\text{E}\right)\left(\text{y/}\left[{\left(\text{x}-\text{a}\right)}^2+{\text{y}}^{\text{2}}\right]-\text{y/}\left[{\left(\text{x}-\text{a}\right)}^2+{\text{y}}^{\text{2}}\right]\right)$Equ. 16

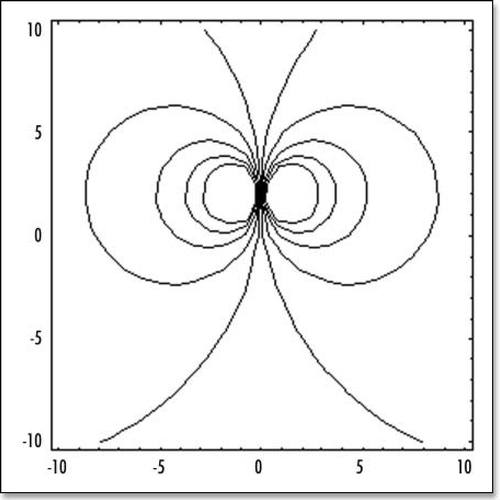
If there were only one force term, the “flow” would be as in Figure 5, since there are two forces, the flow is the superposition of two such “flow” maps, albeit with a little shift (Fig 6A). Again, this result is so far exact. The principle simplification is in the distribution of forces, which has been reduced to only two symmetrically pulling forces.

If we add more source terms along Kohler's sickle, for example, six force terms alined along Kohler's sickle, we found a slightly modified deformation field, but almost indistinguishable (Fig. 6B). (NB: Adding more terms to the description of Kohler's sickle is analogous, in magnetism problems, to considering a coil made of several loops, instead of one single loop, or to replacing a single magnetic dipole by a magnetic needle of a certain length. One may think of a number of cells, or cell aggregates, pulling inside Kohler's sickle: each of these cells can be treated as a single dipolar loop).

Blastodisc Shape

Now, we can find the evolution of the shape of the blastodisc, by advecting the rim of the blastodisc in this flow. In order to do so, we simply define the circle of the blastodisc boundary, and let it perform a few steps of displacement, at a speed given by curl(#x003C8;) = (d_y#x003C8;, −d_x#x003C8;). In detail, the parameters in our analytical model are : the distance of Kohler's sickle to the center of symmetry of the blastodisc (probably the center of the blastocoel); the magnitude of the force, and the lateral extent of Kohler's sickle (which amounts to 2a).

The result for reasonable values of the parameters is seen in Figures 7 and 8, which fits remarkably the evolution of the avian blastodisc. Especially, the caudal region tends to extend, while a flow towards Kohler's sickle creates a “strangled” region. In this model, the very existence of a tail has an hydrodynamic origin. However, not many such steps are allowed, since one should recalculate (“self-consistency”) the force distribution on the deformed configuration, in order to recalculate the corresponding flow, etc. This we shall not do here. Before going to the next section, we should acknowledge that we may expect the blastodisc and the rest of the egg membrane not to have the same mechanical properties, also, the posterior and anterior regions should have a different E (because of partial delamination) therefore, some regional differences in mechanical parameters should be introduced between the inside and the outside of the blastodisc and between the north and the south of the blastodisc, which makes the problem not tractable analytically. However, at this stage of description, I believe that the shape of the blastodisc during gastrulation, which appears in Figure 7 suffices to demonstrate the relevance of this approach.

Origin of Primitive Streak Formation

We address in this paragraph the question of why a streak will form. (In the next part we will address the question of ingression and streak retreat).

We start from the “flow” of the epiblast, which is actually a step-by-step deformation under stress. We have a pulling force exerted by the “flow” in the region of Kohler's sickle. If we isolate by gedanken experiment, an infinitesimal volume of matter in the sickle region, we see that this element of matter is divided into two components, the presumptive mesoderm, which is pulled forward towards Kohler's sickle, and the extra cellular matrix, which bears the traction which allows the presumptive mesoderm to move forward. This traction can be intuitively understood if one remembers that the cells move by filopodia traction. The dynamics of filopodia extension and contraction amounts to a solid tensile stress on the stiffer extra cellular matrix, by which the cells pull themselves forward, while the cell body deformation amounts to the strain component of the “Poiseuille” deformation (Figs. 3 and 4).

It is rarely realized that cell motility in one direction on a medium requires a traction on the medium in the opposite direction, by the principle of action and reaction (Newton's law). If one thinks of a cell moving on a Petri dish, the Petri dish is solid, and holds easily the tension exerted by the cell. However, if the Petri dish were very soft, then the motility activity would simply pull the substrate towards the cell, and the cell would not move. This is much like running a car: the road undergoes a very strong pull, by which the car moves forward; if the road is soft (e.g., muddy), the car does not move forward: the soil is pulled under the wheels. To be honest, this fact has actually been used in this field for 20 years to detect and study cellular traction. Indeed, a now classical means to study the traction force exerted by cells on the extracellular medium consists in depositing and anchoring cells to very soft substrates, like very thin polymer silicon membranes. These thin films are so thin that they wrinkle under the traction exerted by the cells. Optical visualization of the wrinkles (e.g., by Nomarski contrast) enables one to count the wrinkles, and hence to measure the magnitude of the force exerted by the cells. Such techniques, and alternative ones, have been reviewed recently.11

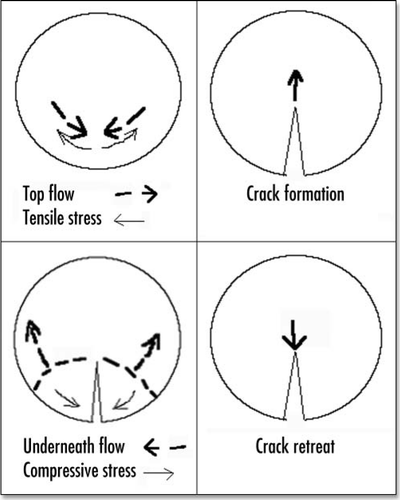
If we now turn to the “flow” map we see that the traction force exerted on the tissue which allows the motion is simply opposed to the stress generated by the “flow”. Therefore, in order to find the stress field, it suffices to find the displacement U, and then to form the stress field. Although these could be written analytically, they contain rational polynomials up to the 8^th power in x and y, this is why we simply give a numerical solution by Mathematica (Fig. 9) which shows the map of stress components σ and σ_yy (the x axis being the vertical axis in the Fig. 9). In this figure, the color gives the magnitude of the component (black is tensile, white is compressive), but remember that the stress is a tensor, and therefore, at each point in Figure 9A, the quantity being considered is a vector oriented along x (σ_xx) while in 9B the quantity considered is a vector oriented along y (σ_yy). We see that along the “caudal line” represented by the axis of left/right symmetry of the blastodisc, the stress is tensile, and oriented orthoradially. The stress map is formed of large oval lobes of high magnitude stress laying over this axis. In the perpendicular direction, the stress is compressive. Therefore, for a distribution of forces forming two dipoles which contract the tissue towards the caudal pole, the force on the extra cellular matrix actually stretches the mid line. If we assume that above a tensile stress σ* the extra cellular matrix cracks, a “primitive streak” will open which will nucleate at the center of traction, which is the intersection of Kohler's sickle with the AP axis, and will next propagate along the AP axis in the P→A direction, and also in the caudal direction, if Kohler's sickle is not strictly caudal at the moment of cracking. This is analogous to a paper cracking perpendicularly to the edge, as fingers pull two parts of a sheet asunder; this is more than a metaphore in that the blastodisc behaves as the paper sheet, and the traction centers as two hands pulling apart, in an actual piece of paper, the stress field is also probably like in Figure 9.

It is not entirely clear to the author whether in the true world, the primitive streak propagates in the P→A or A→P direction. At www.gastrulation.org one finds in display a movie movie15_3.avi, in which the primitive streak seems to open in the A→P direction, from Hensen's node (although Hensen's node progresses towards the anterior part, the mesoderm ingression starts first at Hensen's node, and eventually reaches the caudal pole). If this is true, then the center of the pattern in Figures 6 and 9 is Hensen's node, and the apparent forward growth is in fact due to elongation of the caudal part. This center in Figures 6 and 9 is characteristic in that it is the spot of highest stress in all directions : quite tensile in one direction, quite compressive in the other. In this view, Hensen's node is instructed by mechanical forces.

Mesoderm Ingression and Primitive Streak Retreat

We now try to explain what may happen next. Especially, we wish to address the question of mesoderm ingression and “flow” underneath. This we shall do only qualitatively. By the presence of the crack, the tissue can no longer withstand the filopodia traction, as a consequence, the cells present on the epiblast can no longer flow towards the mid-line (A→P axis), they can only contract (buckling) the lip of the crack which now stands free, but cannot move. This is a natural explanation of why the lip of the crack appears first as a thicknening in the region of the presumptive primitive streak. Also, the orthoradial component of the force term oriented towards six o'clock is cancelled. There remains in the epiblast plane an orthogonal force pulling towards the center of the blastodisc. This can be understood intuitively by the fact that this force is the one which the ECM can still sustain : if one imagines a blanket with a big cleft, it can be used to crawl only along the direction of the cleft lip. This means that after the opening of the streak, the force generating the vortex of the epiblast is mainly oriented towards the center of the embryo. This is a natural explanation of why the flow map changes from a flow oriented towards six o'clock, to a flow which is more oriented towards the center of the blastodisc. Now, the situation is entirely different in the ingressing mesoderm, indeed, the ingressing mesoderm, as it makes a vertical U-turn, can crawl on the ECM, if it flows in the opposite direction as the direction from which it came in.

Let us simplify the problem and consider a strip of constant length, which breaks in two when stretched (Figs. 10 and 11). We suppose that the tip of the strip folds down and then crawls backwards towards its middle, making a U-turn, we see that the average stress is first tensile. At the crack moment, the stress is released, and the filopodia traction can only generate a buckling of the very tip. As the cells ingress inside the crack, the tension at the tip decreases because the crack region undergoes the compressive stress exerted by the ingressed layer, it is then less tensed than prior to cracking. When exactly the same area is present on top and underneath, the total force is the tensile stress on top, minus the compressive stress underneath, which add up to zero. Hence, the tissue returns gently to its equilibrium, and the lips close up as the cells underneath crawl. As the lips close up, the tip of the crack performs the inverse path, and the primitive streak retreats (Fig. 12). In the end, a two-layered tissue is formed, in which the tension is equilibrated, although the two layered strip may still feel shear.

In conclusion of this section, we see that if there is a localized cell attractor, it induces a tensile center, which can “open”, in a process analogous to crack opening. The crack opens a hole for the cells, which ingress, up to the point where the internal layer has the same area as the external layer, and the process equilibrates itself spontaneously. At the moment of cracking, a buckling occurs at the lip of the hole (or crack) which exhibits a thickening, which is released as the cells ingress. The ingression process may induce a partial or complete reclosing of the cavity or “crack”, and the final picture is a two layered pouch with a pinhole; contact inhibition of a cell type towards apical-apical connections may leave the hole open. The model described here may naturally explain other instances of gastrulation, or invagination, such as pore formation.

Vitelline Arteries

It is a classical observation in avian embryology that the vitelline arteries form in the narrow region of the area pellucida (Fig. 13). The area pellucida has inherited from the gastrulation movement a typical “eight” shape, and the vitelline arteries first prune in the region of the “funnel” (one on each side) made by the constriction in the middle of the eight (Fig. 14A). Please note that this eight is not symmetrical, and the top is larger than the bottom.

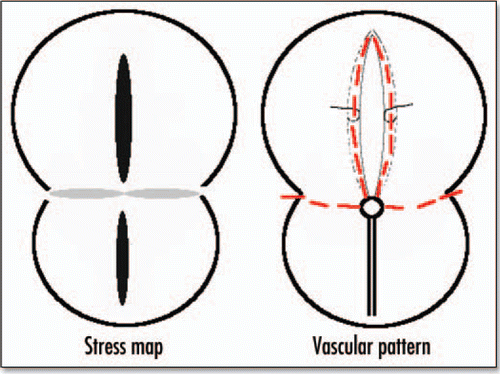
I stated, in the previous paragraphs, that the theoretical deformation of the gastrula should incorporate self-consistently the change in shape of Kohler's sickle, and I avoided showing later stages of the blastodisc shape. However, if we do pursue the deformation of the blastodisc, we find, amazingly, an 8 shape with a large “head” and a small “belly” (Fig. 14B). In between, in the region of the nip of the eight, the boundary of the blastodisc is squeezed in, and forms a stretched line of tissue. This tissue is stretched towards the nip (funnel effect), but compressed in the perpendicular direction (because of mass conservation). If we summarize the pattern of stress, and the corresponding deformation (Fig. 15A), and summarize the pattern of vessels (Fig. 15B) we find a clear correspondence. The eight shape of the area pellucida is well explained by the vortex movement, and the position of vessels is well explained by the stress map. It is likely that the high stresses felt at right angles by the cells accelerate the morphogenetic events, and lays the presumptive path of the vitelline arteries. If this is correct, it is the first description of a mechanical prepattern which is laid down by a dynamic vortex.

The Embryo Proper

Finally, I evoked the induction of the embryo body by Hensen's node above, for which people still search for morphogenes. If our view that the 8 shape of the embryo reflects the contraction pattern and flow during gastrulation (Fig. 14), it then appears that Hensen's node is actually the center of the contraction, which can be seen in (Fig. 6 or 9). As mentioned earlier, there exist two lobes of uniaxial (orthoradial) stress lying over the AP axis. The primitive streak would naturally be the caudal lobe, and the embryo axis the more anterior lobe. In this view, one should explain the delay between streak formation and embryo body formation, this may simply be due to the stiffer nature of the anterior part, which is not delaminated. In the anterior part, crack formation does not lead to an ingression, but only to a buckling of the lips (Fig. 15B), an image which fits with the formation of the presumptive cardiac tubes an dorsal aortas, while the groove forms the presumptive chord, a pattern ending with three tubes, corresponding to heart and spinal rudiments. In the region of the middle of the embryo, where the endoderm and ectoderm delaminate, the cardiac and dorsal tubes will be topologically connected to the mesoderm, because the buckling of the endoderm lip, in the region of the middle where endoderm and ectoderm are separated by mesoderm forms a curly lip which wraps some mesoderm, by the very apex of the crack. At the other end, the tube exit is oriented towards the opposite pole of the embryo (anterior pole). These topological connections orient naturally the outflow of blood from the dorsal aortas into the presumptive vitelline arteries formed by the mesoderm stretched edge in the nip of the 8. The venous inflow is at one end, and the arterous outflow in the middle of the embryo and at right angles thus allowing the flow to drain a great part of the yolk sac, as observed.

In the end, the sequence [flow towards the posterior pole⇒crack opens⇒mesoderm ingresses in the crack of the posterior pole⇒crack retreats⇒crack opens in the anterior pole⇒lips buckle and form tubes along the crack of the anterior pole⇒connection of tubes to the funnels of mesoderm] has a flavour of a completely mechanical and automatic phenomenon. It requires only very few ingredients : (1) an attractant pole for a motile epiblast; (2) a delaminated blastula below the attractant pole (3) a well adjusted criterion for crack opening under stress.

The simplicity, and the automatic chaining of the events may explain a rapid evolutionary jump from a-gastrulated to gastrulated animals. It also explains the robustness of the process, and it gives a possible origin to a number of anomalies, such as spina bifida, or two body embryos. The crack model gives also an obvious explanation of why the cardiac tubes, the aortas etc. come in pairs.

This model gives insight into other types of gastrulation, even if they are not flat, for the following reason: although other blastulas may be spherical, the conceptual separation between the cellular part, and the extra cellular compartement remains. The modelling of the shell by a “flow” of a thin solid sheet is not modified, except for the underlying geometry (spherical instead of flat). The role played by attraction centers, and the possibility of a crack opening and invagination is qualitatively similar, although it can hardly be calculated. The presence of a stiff matrix around cells gives an important role to shear forces, because a cell crawling through narrow gaps of a stiff medium undergoes mostly shear forces.

In the model presented here, the laying down of the body axis, and of the yolk sac vascular pattern at right angles, is deeply rooted in conservation laws of hydrodynamics (contraction in one direction implies dilation in the other).

A model of crack propagation has been proposed for formation of leaf venation by Couder,12 which is somewhat related to what was discussed here, except that in Couder's model, there is no mass flow, and the stresses are supposed to be all compressive. In Couder's model, veins form everywhere by self-organization, there is no pulling pole. In some sense, the presence of a pulling pole in animal embryos determines the position of a single large “vein” of the “leaf” which the blastodisc is. This large “vein” becomes the primitive streak and the embryo axis, in this spirit, Figure 15A may loosely evoke the fomation of an oak leaf. This comparison sounds more like a poetic metaphore than a scientific truth, because the material properties of plants are quite different from animals, and because many more events occur after gastrulation.

Of course, many other processes may be taken over by genetical loops.

Figures and Tables

Figure 1 Schematic view of the blastodisc on top of the yolk.

Figure 2 Schematic view of the blastodisc prior to gastrulation, and just after formation of the primitive streak and Hensen's node.

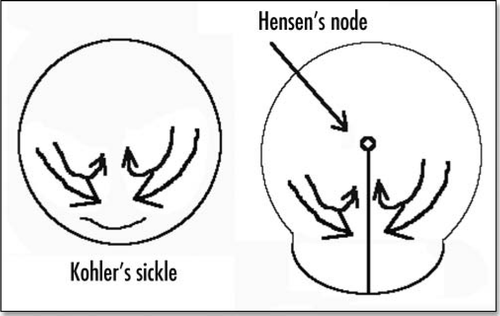
Figure 3 (A) When a true liquid is pushed between two glass plates, it flows with a parabolic profile of fluid speed. (B) However when a solid is pushed between plates, it will only deform, and adopt a parabolic deformation.

Figure 4 Schematic representation of a cell embedded between extracellular membranes, and crawling towards the posterior pole. A little elementary volume of tissue undergoes a tensile stress. The excess of filopodia to the right represents the filopodia gradient. The posterior pole undergoes tractions from both sides, hence it sees a tensile force twice as big as the tensile force generated by the filopodia.

Figure 5 The stream lines with one single source of force (located in the nip) oriented vertically.

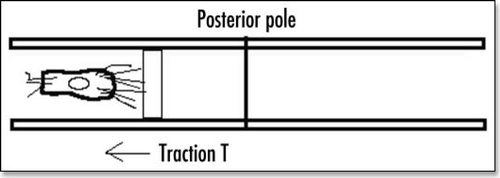
Figure 6 The stream lines with symmetrical forces, oriented face to face. These model the attractive (contractile) effect of Kohler's sickle. (A) depicts schematically the situation. (B) shows the stream lines for two centers of forces (one on each side, top and bottom, located at −R/10 and +R/10). (C) shows the streamlines for six aligned centers of forces modeling Kohler's sickle as a line of pulling agents (located at ±R/30, ±2R/30, ±R/10).

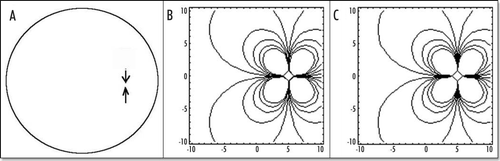
Figure 7 (A) Typical small deformation of the blastodisc, as a consequence of this “flow”. It is obtained by starting with a circle, and let it “flow” in the “flow” map. In this calculation, the forces were located at a distance 7/10 of R towards the caudal pole, and they were spanning a width equal to 2/10 of R on each side. The deformation creates a thin tail, and a bigger anterior part, as observed. The tail extends caudaly (so to speak) and the embryo body is strangled on its perimeter, with an orientation towards the nip of Kohler's sickle, as observed. (B) If two more time steps are performed one finds the following evolution. However, the force itself is no longer located simply along a straight segment, therefore the calculation cannot be pursued without calculating self-consistently the force distribution.

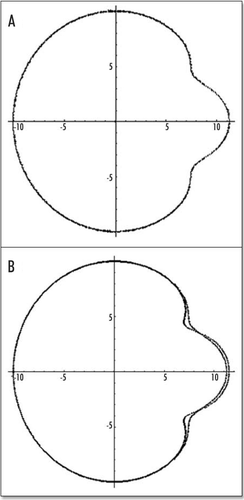
Figure 8 The actual shape of the tail depends on the location of the forces inside the caudal pole (the distance to the center of the blastodisc), and on the size of the segment which exerts the force. In (A), the force is located at 2/10 of R, in the caudal half, in this case, the tail part is almost as big as the head part. In (B), the force is located closer to the caudal pole, by 8/10 of R, the “flow” generates only a little tail.

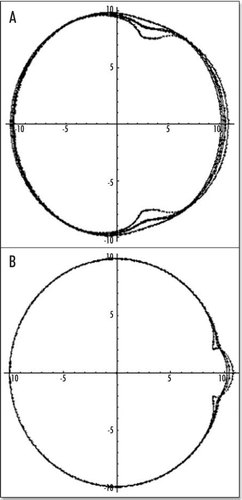
Figure 9 (A–C) The distribution of stress inside the blastodisc, in the region of Kohler's sickle. (A) σ_xx; (B) σ_yy. (A) shows that the highest stress (dark) inside the blastodisc in the region of Kohler's sickle, is tensile orthoradially (the biggest component is the derivative of the orthoradial deformation). In simple terms, the extracellular matrix is torn apart by the two halves which pull the cells towards Kohler's sickle. Please pay attention to the fact that the other component of the stress is compressive in the region of Kohler's sickle. (C) depicts the tensile component along the orthoradial direction of the stress field in the blastoderm, in order to understand better (A). Along the AP axis, and on either sides of Kohler's sickle, the region of high stress is the caudal axis itself, and the stress is oriented orthoradially: this is exactly the best condition for a crack. In other areas, the stress does not have a tensile component oriented perpendicularly to the axis defined by the region of high magnitude. For example, if one looks at the darker areas defined by the high magnitude of σ_yy (B) one sees that these areas form large lobes similar to the ones for σ_xx, but these are not oriented perpendicularly to the y axis. Due to numerical artefacts, the very center of the calculation (the location of the forces) appears homogenously white (A) or black (B), but one should prolongate and complete the lobes by thought.

Figure 10 Situation after opening of the “crack”.

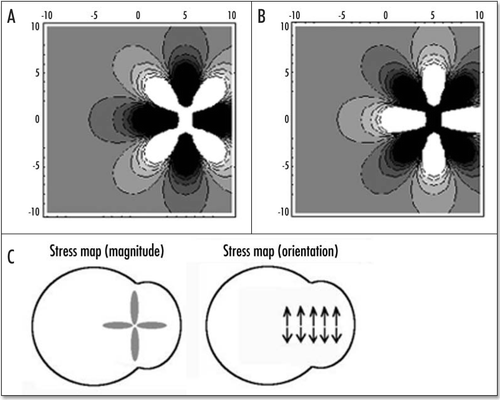
Figure 11 Very simplified picture of a strip of cells which is put in tension, then cracked. As cells ingress and crawl backwards, the region of the crack feels less tension.

Figure 12 Shematic view of crack opening and retreat.

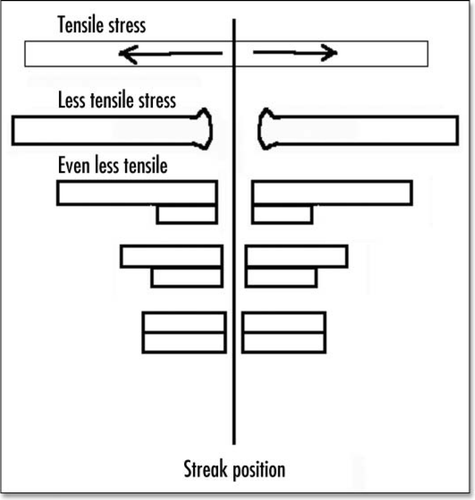
Figure 13 A typical chicken embryo by day 4, showing the eight shaped area pellucida, and the location of the vitteline arteries, which always form in the region of the “funnel” of the eight.

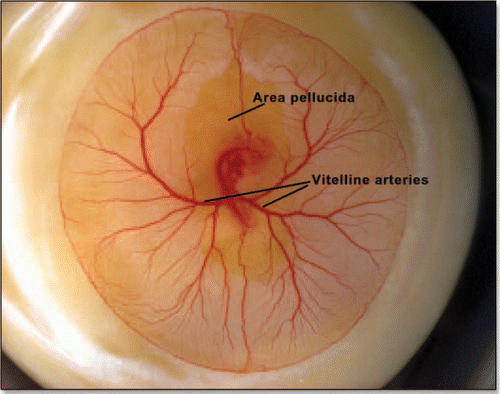
Figure 14 (A) A typical eight shaped area pellucida seen in the center of the yolk sac, surrounding the embryo, at day 1. The head is towards the top (12 o'clock), the tail towards the bottom. Blood islands are visible in the yolk sac The arteries will form the next day in the region of the nip of the eight. (Image courtesy of Lenoble F, U. Maastricht). (B) A typical theoretical blastodisc shape, if several deformation steps are performed (the AP axis is horizontal). A sector of the circle is actually sucked towards the nip where Kohler's sickle is exerting its force, while the tail extends caudaly. In this picture, the blastodisc adopts progressively an eight shape with a singular region in the region of the nip of the eight. In the center of this nip, one finds the center of the vortices seen in Figure 6B and C. This may be the origin of the prepattern of vitteline arteries. However, the calculated pattern is not as elongated as observed. In the actual embryo, there is obviously an additional extension in the AP direction, which is absent from this model. If we assume that this additional deformation does not change the global topology of the problem (mere change in aspect ratio), we can temptatively consider the center of pull as Hensen's node, and the two stressed areas anterior and posterior, as the presumptive primitive streak, and presumptive embryo body (horizontal gray lobes in Figure 9C. A likely reason why they undergo differente fates after cracking is in that the anterior part is not delaminated.

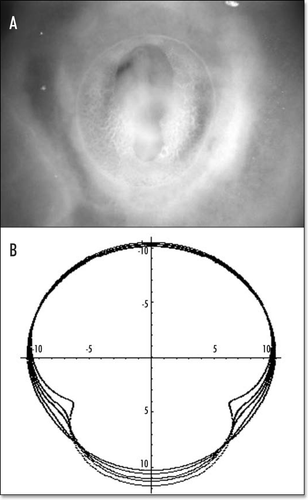
Figure 15 Correspondence between the stress map during gastrulation, and the eventual pattern of blood vessels. The black lobe corresponds to strong tension in x, the gray correspond to strong compression in y, the lower lobe leads to the primitive streak and mesoderm ingression, the upper lobe to embryo axis, and the perpendicular lines to vitelline arteries.