What is the weakest topology in which feedback stability is robust?

References

• Mari , F. D. , Ober , R. , Hinrichsen , D. and Martensson , B. 1990 . “ Topological aspects of robust control ” . In Control of uncertain systems , 57 – 67 . Boston: Birkhauser .
   Google Scholar
• Vidyasagar , M . 1984 . The graph metric for unstable plants and robustness estimates for feedback stability . IEEE Transactions on Automatatic Control , 29 : 403 – 417 . doi: 10.1109/TAC.1984.1103547
   Web of Science ®Google Scholar
• Vidyasagar , M . 1985 . Control system synthesis: A factorization approach , Cambridge: MIT Press .
   Google Scholar
• Vidyasagar , M . 1996 . A brief history of the graph topology . European Journal of Control , 2 : 80 – 87 . doi: 10.1016/S0947-3580(96)70032-8
   Web of Science ®Google Scholar
• Vidyasagar , M. and Anderson , B . 1989 . Approximation and stabilization of distributed systems by lumped systems . Systems & Control Letters , 12 : 95 – 101 . doi: 10.1016/0167-6911(89)90001-7
   Web of Science ®Google Scholar
• Vinnicombe , G . 1999 . Uncertainty and feedback: 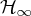loop shaping and the ν-gap metric , London: Imperial College Press .
   Google Scholar