Theoretical model for laser ablation outcome predictions in brain: calibration and validation on clinical MR thermometry images

Figures & data

Figure 1. Subfigure (A) is the model’s temperature prediction that optimises the objective function, Dice similarity coefficient (DSC). Subfigure (A) is juxtaposed with a time frame from clinical MR thermometry that is near steady state, Subfigure (B). Subfigure (C) is the 57 °C isotherm map, showing where the thermometry and model overlap or do not. The threshold map of subfigure (C) is used to compute DSC. For this image, DSC is 0.88. Subfigure (D) displays the global optimisation of the model to this particular patient’s thermal dataset, seeking to optimise DSC. The vertical axis is the values of perfusion, ω, and the horizontal axis is the values of the effective optical coefficient, μ_eff. The single point that produces optimal DSC is the dot in subfigure (D), or μ_eff=166 m⁻¹ and ω = 9.5 kg m⁻³ s⁻¹.

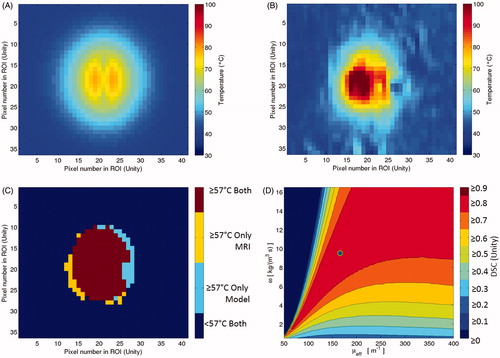
Figure 2. This diagram illustrates the four major components of the global optimisation, using the four images of Figures 1. The gold standard measurement is the MR thermometry from a time point near steady state. This thermal image is compared to the steady state kernel via DSC of the 57 °C isotherms. The kernel is run with 11 400 μ_eff–ω values; each model realisation reports a DSC value and is recorded in the optimisation map at right.

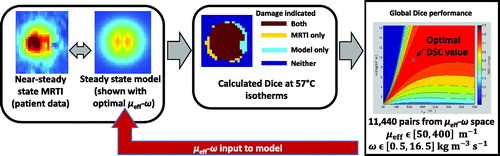
Figure 3. This is a cartoon demonstration of the superposition of individual datasets’ global optimisation in μ_eff–ω space. Each dataset’s optimisation performance, e.g. (A) and (B), can be superimposed pixel-wise in μ_eff–ω space to create an optimisation vector map (C). This optimisation vector map has N = 20 individual optimisation results for every sampled point in μ_eff–ω space. At every point in the optimisation vector map, descriptive statistics can describe the distribution’s behaviour at that μ_eff–ω point, see Figure 4.

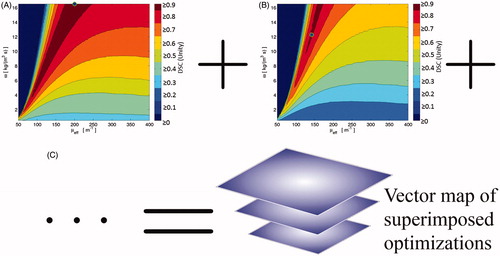
Figure 4. These are the descriptive statistic maps based on the vector map, described in Figure 3. The diamond icons mark the naive literature value choice, μ_eff=180 m^–1 and ω = 6 kg m^–3 s^–1. (A) is the mean; (B) is the median; (C) is the standard deviation; (D) is the number of individual patient datasets that pass DSC ≥0.7.

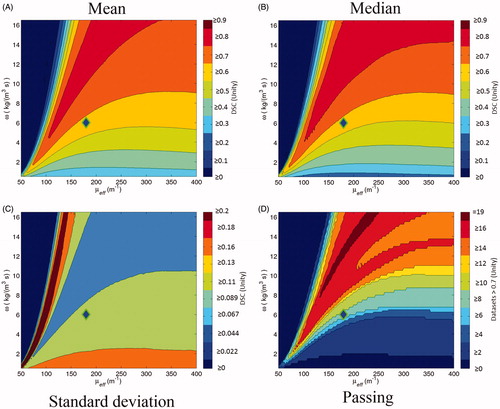
Figure 5. This scatter plot indicates the points in μ_eff–ω space that create optimal DSC values for individual datasets among the N = 20 datasets. There is a simple linear regression fit line (in blue) of the 18 optimal points (markers are blue with green outlines) that define the line. The fit line’s details are listed in the Results. There are two clearly outlying optimal points, isolated to the figure's right side. These points are excluded from the fit line, but are included in leave-one-out cross-validation. The scatter plot and fit line are superimposed over the mean of the DSC vector map; i.e. Figure 4(A).

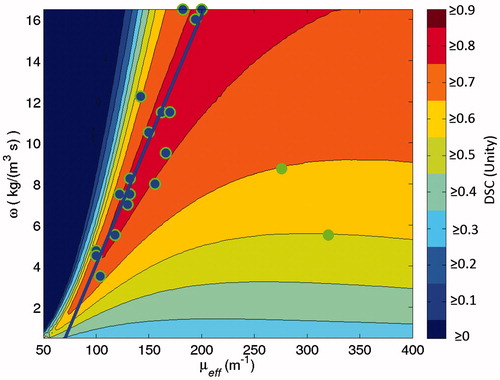
Figure 6. This is a box-and-whisker plot demonstrating the model’s sensitivity to isotherm choice during optimisation; each row represents the distribution of N = 20 patient cohort’s DSC performance during optimisation while using a particular isotherm temperature. 57 °C is the choice implemented in the rest of the work. In the box-and-whisker plot, the solid dots are the minima and maxima, i.e. the ends of the whiskers. The box is the 95% confidence interval and the line within the box is the median. A single dataset among the cohort is not robust with varied isotherm threshold. It is the leftmost outlier and performs worse with rising isotherm threshold, especially at 58 °C and higher. The other datasets do not vary much with isotherm choice.

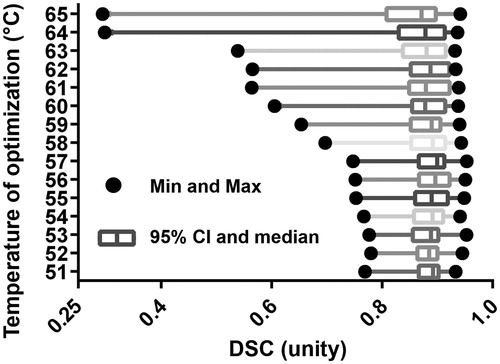
Table 1. Here are the descriptive statistics for DSC performance by using naïve literature values, optimised parameters, and during leave-one-out cross-validation using the vector map method for N = 20 datasets.

Descriptive statistic	Dice Naïve (Unity)	Dice opt. (Unity)	Dice LOOCV (Unity)
Minimum	0.45	0.75	0.59
25%-ile	0.61	0.87	0.77
Median	0.66	0.90	0.85
75%-ile	0.77	0.91	0.88
Maximum	0.86	0.95	0.93
DSC ≥0.7	8	20	19
Mean	0.67	0.89	0.82
Standard deviation	0.11	0.047	0.089
Skewness	−0.23	−1.3	−1.0
Kurtosis	2.3	5.4	3.6

The optimal column represents the best possible DSC performance that the steady state model can achieve within the μ_eff–ω parameter space explored. Note that all DSC, skewness, and kurtosis quantities are unitless. “%-ile” refers to percentiles; e.g. 25%-ile means the dataset’s DSC performance exceeds 25% of the population DSC values in ascending ranked order. DSC: Dice similarity coefficient; naïve: naïve literature values were used in model; opt.: optimal Dice similarity coefficient possible for model; LOOCV: model performance during leave-one-out cross-validation.

Figure 7. For the entire N = 20 cohort, this Figure displays the simulated predictive performance of the globally optimised model during leave-one-out cross-validation (solid line) versus a naïve literature value parameter choice (dashed line). A greater the area-under-the-curve, which is synonymous with the mean performance, indicates better performance.

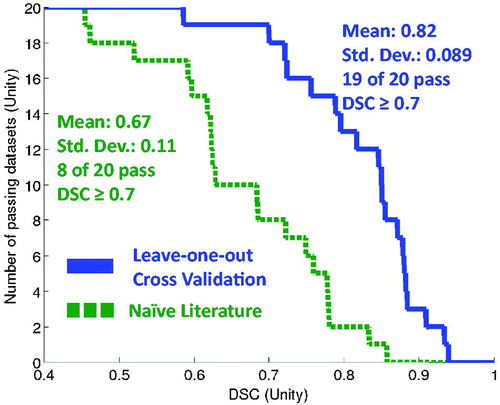
Table 2. These percentiles correspond to several interesting DSC thresholds using the N = 20 datasets.

DSC threshold (Unity)	DSC Naïve (%-ile)	DSC opt. (%-ile)	DSC LOOCV (%-ile)
0.5	11	0	0
0.6	23	0	3.1
0.7	59	0	7.5
0.8	89	5.9	34
0.85	96	13	49
0.9	100	51	86
0.95	100	95	100
0.975	100	100	100

The columns refer to the same datasets described in Table 1. The smaller the percentile value, the better the model’s performance. "0" indicates all values pass at the given threshold; “100” indicates no values pass. DSC: Dice similarity coefficient; naïve: naïve literature values were used in model; opt.: optimal Dice similarity coefficient possible for model; LOOCV: model performance during leave-one-out cross-validation.